表題のような問題を解く必要があったので調べたらできまして、以下のようににツイートしたところニーズがあるとのことだったので記事にしてコードを公開します。
Processingで(p5でもいいんだけど)何度かrotateしてtranslateした座標が元の座標系から見てどういうxyz値になるか知る方法の需要あるかな?(記事にするか迷う)
— 山辺真幸/データビジュアライズデザイナー (@masakick) November 19, 2021
サンプルコード
はじめに
3次元空間上のある点に座標系の回転変換を加えた後、元の座標系から見てどの座標に移ったかを調べるには、Quaternion(クォータニオン)を使うと割と簡単にできるのですが、Processingでは標準でQuaternionをサポートしていない(はず)なので、Quaternionクラスを用意して使っていくことになります。
Quaternion自体の解説はこの記事では扱いません。とりあえず使い方だけわかればいいので、本格的に知りたい場合は、線形代数やゲーム系のCGなどの書籍などでは詳しい解説が読めると思います。
Quaternionクラスを用意する
Quaternionクラスを用意すると言っても、kyndさんが公開してくれているのでありがたく使用します。
Processingライブラリとして提供されているわけではないので、sketchに「Quaternion」というタブを新規で作ってそこにコピペして使います。(スペルミスに注意)
詳細についてはサンプルコードのコメントで記述しますが、流れとしては次のようなことをやっています。
- 原点を画面中央にセットする。
- 座標系を保存する(pushMatrix)
- rotateを3回実行して座標系を回転させる
- 回転させた後にtranslateを使って(50,-50,0)の位置に原点を移動してそこに緑のキューブを置く
- 回転前の座標に戻す(popMatrix)
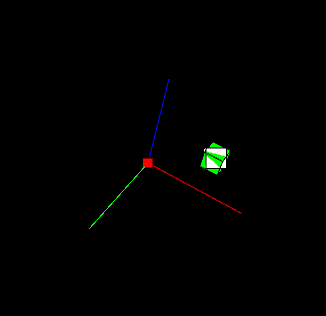
そうすると、元の座標系で緑のキューブの位置はどこですか?となるので、Quaternionを使って計算し、その座標に白いキューブを置いています。結果的には、緑のキューブと白のキューブがぴったり重なって表示されます。(ただし白いキューブに回転は加わっていないので正面を向いています。)
実行結果
サンプルコード
//三次元空間上のある点(target)に座標系の回転変換を加えた後、
//元の座標系から見てどの座標に移ったかを調べる
PVector target;
Quaternion q;
PVector axisX;
PVector axisY;
PVector axisZ;
void setup(){
size(600,600,P3D);
//座標変換前のx,y,z単位ベクトル(あとで計算に使う)
axisX = new PVector(1,0,0);
axisY = new PVector(0,1,0);
axisZ = new PVector(0,0,1);
//変換前の座標
target = new PVector(50,-50,0);
//クォータニオンの初期化
q = new Quaternion();
q.setAngleAxis( 0, new PVector(0,0,0) );
noLoop();
}
void draw(){
background(0,0,0);
// -- ここから準備
//画面の中心に原点を持ってくる
translate(width/2, height/2,0);
//画面手前(z=500)から原点(0,0,0)をに向かってカメラをセット
camera(0,0,500,0,0,0,0,1,0);
//原点の目印(赤いキューブ)
fill(255,0,0);
box(10);
// -- ここまで準備
// -- ここから本題
//回転前に座標系を保存(通常通り)
pushMatrix();
//座標系をX軸中心に45度、Y軸中心に10度、Z軸に30度回転(通常通り)
rotateX( radians(45) ); //X軸を中心に45°
rotateY( radians(10) ); //Y軸を中心に10°
rotateZ( radians(30) ); //Z軸を中心に30°
//回転情報を上と同じように順にクォータニオンに記録していく(ここ重要。あとで使う)
q = q.mult( new Quaternion( radians(45), q.mult(axisX) ) ); //X軸を中心に45°
q = q.mult( new Quaternion( radians(10), q.mult(axisY) ) ); //Y軸を中心に10°
q = q.mult( new Quaternion( radians(30), q.mult(axisZ) ) ); //Z軸を中心に30°
//目的の座標に動かす(通常通り)
translate(target.x, target.y, target.z);
//緑色のキューブを置く(通常通り)
fill(0, 255,0);
box(20);
popMatrix();
//回転前の座標系に戻す(通常通り)
// -- ここから元の座標系における回転変換後の緑のキューブの位置を計算していく
// 1. 回転させた座標系のX軸、Y軸、Z軸が元の座標系でどのようなベクトルになっているかを、クォータニオンを使って調べる(全て単位ベクトル)
PVector newAxisX = q.mult(axisX);
PVector newAxisY = q.mult(axisY);
PVector newAxisZ = q.mult(axisZ);
// 2. 上の各単位ベクトルから緑のキューブの位置を計算
PVector newTarget = PVector.add( PVector.mult(newAxisX,target.x), PVector.mult(newAxisY,target.y), PVector.mult(newAxisZ,target.z) );
println(newTarget); //[ 67.26362, -4.554388, -21.327515 ]という座標に移っていた
//ちなみに、1と2のステップは下記のように1ステップで求めることもできる
//軸がどっちを向いているか知る必要がない場合はこれで事足りる。各軸の方向がわかったほうが良い場合は上。
PVector newTarget2 = q.mult(target);
println(newTarget2); //[ 67.26362, -4.554388, -21.327515 ]
// 3. 座標がわかったので白いキューブを置いてみる(緑のキューブとぴったり重なるはず。ただし、方向は正面を向いている)
pushMatrix();
translate(newTarget.x, newTarget.y, newTarget.z);
fill(255);
box(20);
popMatrix();
// 4. 一応座標軸も書いてみる。赤=X軸、緑=Y軸、青=Z軸
stroke(255,0,0);
line(0,0,0,100*newAxisX.x, 100*newAxisX.y, 100*newAxisX.z);
stroke(0,255,0);
line(0,0,0,100*newAxisY.x, 100*newAxisY.y, 100*newAxisY.z);
stroke(0,0,255);
line(0,0,0,100*newAxisZ.x, 100*newAxisZ.y, 100*newAxisZ.z);
}
以上です。
質問、別解、ご指摘などありましたらコメント歓迎です。
ありがとうございました。