“答えをどうやって決めているのか？” を重みから読み解く
前回は、「CNNモデル の各層の出力が学習中にどう変化するか」 を GIF で眺めました。
あれは “ネットワークの内部が視覚的にどう変換されているか” を見るものでした。
でも実はまだ見ていない “超重要ポイント” が残っています。
今回のテーマ
モデルは最終的に “どうやってクラスを決めているのか・識別をしてるのか？”
その判断根拠を 重み と 中間特徴 から読み解く。
CNNモデル では最終的に、
• logits = FC2( ReLU( FC1( Flatten( Conv2(Conv1(x)) ))))
というパイプラインで 9クラスの生スコア (logits) を出します。
ここではこの中でも特に重要な FC層（全結合層） を見ていきます。
1. まず “FC が何をしているのか” を正確に理解する
Flatten した後の形状は：
• Conv2 → MaxPool2 → Flatten:
• (32, 8, 8) = 2048 個の数値
これを FC1 が次のように扱います：
• FC1: 2048 個 → 64 個の特徴ベクトルへ
つまり、
• FC1[i] = Σ_j ( feature[j] * weight1[i][j] + bias1[i] ) -> iは[0,63]
これを 64種類の線形和 として計算しています。
次に：
• FC2: 64 個の特徴 → 9 クラスのスコア(logit)
つまり、
• logit[k] = Σ_i ( FC1[i] * weight2[k][i] + bias2[k] )
この式こそが「モデルが判断する瞬間」の中身そのもの。
• どの特徴（FC1の64次元）が、どのクラスに効いているのか？
• 今回の入力画像では “どの次元が強く反応し、どのクラスを押し上げたのか”？
• 重み × 特徴 の寄与を “ランキングと可視化” で見えるようにする
こうすることで、 「なぜ (例えば) logit[3] が勝ったのか」 が数字として追っていける。
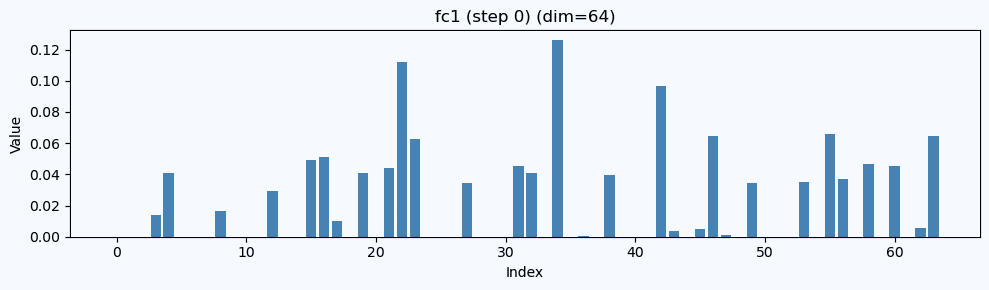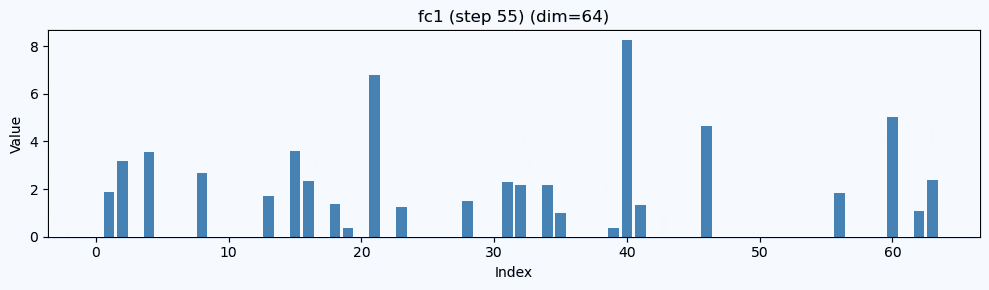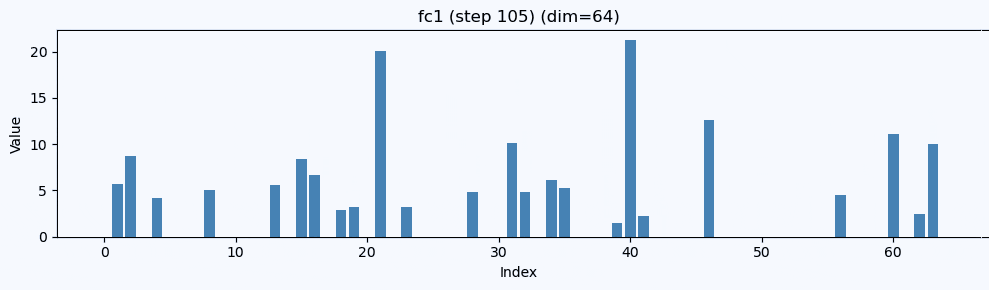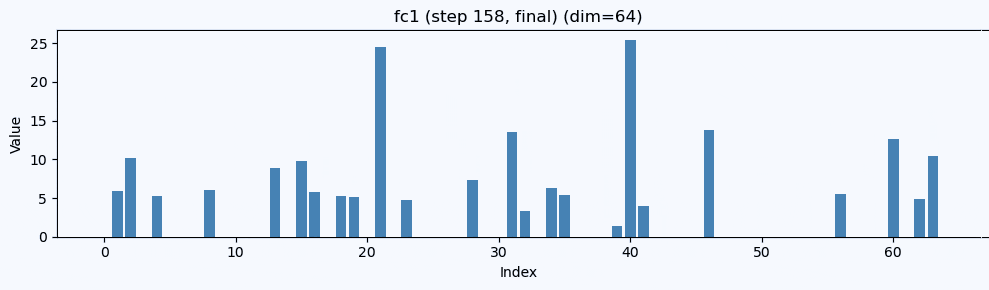
2. Step1： FC1 の出力（64次元）の “どれが効いているか” を見る
前回の結果より、
ここでは、 チャンネル #39 と #20 が強く立ってくる
ちなみにこれは学習過程でこうなるので、seed値を固定していないと再現性はない。
これはつまり、
• Conv1/Conv2/Pool を通して
• ノイズの中から “四角の存在らしき特徴” を抽出し
• FC1 がその特徴を “意味のある次元” に圧縮した
つまり
FC1 が作る 64次元のベクトルは「64個の特徴を表す」というより、
「64個の座標軸の上に入力をどう配置したか」
ということ。
この FC1 出力（64次元）を棒グラフで描く と、
「どの次元が効いているか」が一目でわかります。
FC1ではどの正解ラベルでも#39が強いのが見えます。
3. Step2：FC2 の重みを見る
「各クラスはどの特徴をどれだけ重視するか？」
FC2 の weight2[k] は、9クラス × 64次元。つまり、
• 各クラスは、64個の特徴を “どれだけ採用するか” を学習している
• 例えばクラス3に対しては、39番目の特徴に強い正の重みが付いている
という可能性がある。
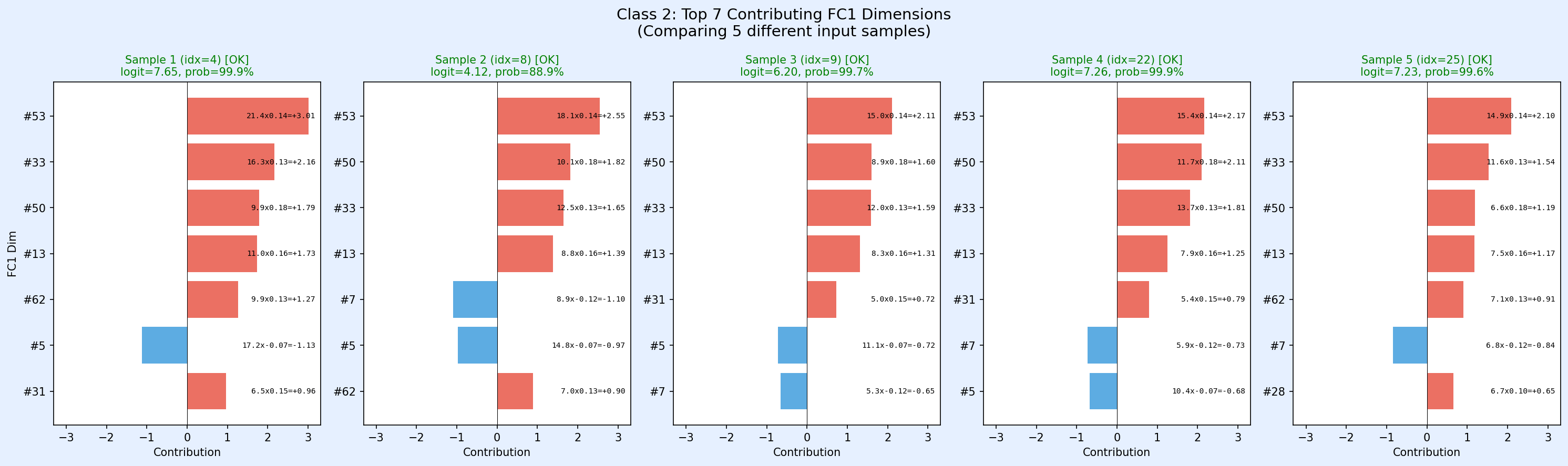
見てみました。FC2の出力からみてFC1の出力がどれだけ寄与してるかをみてみます。
寄与度は、
• FC1の出力 × FC2 重み
• -> contribution[k][i] = FC1[i] * weight2[k][i]
で計算できます。これはモデルが正解ラベルを当てる上での “判断根拠” そのものです。
これをみるとある程度、
• どの FC1 次元が（例えば#39が）
• logit[3] を押し上げたか
• 逆に他のクラスをどれだけ抑え込んだか
が数字とグラフでわかる。
39番目は結構どこにでも最終寄与として高いものとしてでてるのわかります。でもパターンは違いますね。
これはクラスごとの “性格” や “好みの特徴” のようなものといったところでしょうか
実際これではあまりわからない気もしますが、これを同じ正解ラベルでも四角の位置が微妙に違ったり、背景ノイズのパターンが違うものでいくつかサンプルをとってみてます。
正解ラベル0を5パターン見てみます
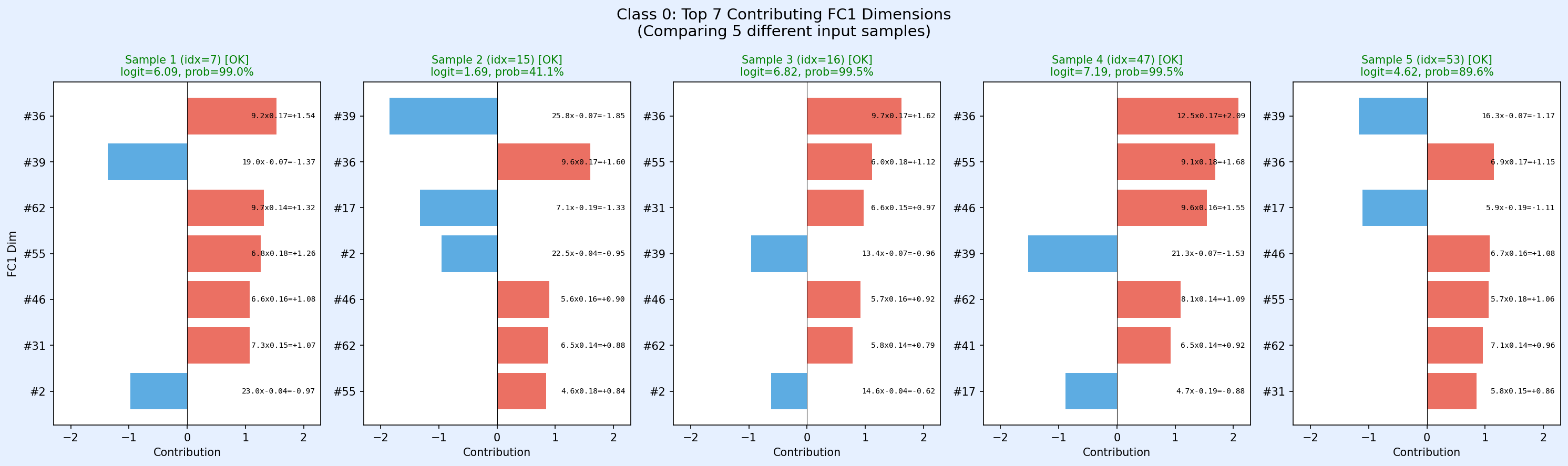
#36が決め手になってるように見えますね。#39に至ってはネガティブに効いてます。つまり#39は正解ラベル0じゃないって言いたい側に働いてる。でも結局は64個の特徴の投票で決まるので、#39の意見だけでは決定はされないという感じでしょうか？
各特徴は「押し上げる」だけではなく「押し下げる」役割も持っている
ある特徴が大きくても、そのクラスに対する重みが負ならそのクラスの logit を強く下げる方向に働く
正解ラベル1
#2,#7,#39が寄与率が高いです。
正解ラベル2
圧倒的に#53,#50,#33が支配的です。
このようにして、「最終判断にどの特徴がどれだけ貢献したか」 がクリアにわかる。
またFC2の出力 Logits (9,)で一番大きい値がモデルの出した回答になるので、結局これらの合計(非負のみではなく負も考慮に入れて）で決まることになります。
例えば正解クラスが6の時に、Logits (9,) で6以外も含めて全てでどのようになってるかを見てると、
クラス6は意外と振り切ってる値はなく平均的に全部高いって感じで、振り切ってるものだけで見れば他のクラスが正解でもおかしくないような分布です。ただ、負も含めて合計で判断することになるのでここではクラス6が 投票 で勝つことになります。補足すると、実際には「寄与度の合計」が最大のクラスが選ばれており、すべての特徴 × 重み の総和がいちばん大きかったクラスが “勝者のクラス” になる。
4.考察
同じ正解クラスでも入力の四角の位置やノイズパターンが変わるとテンソルの出力が変わります。今回はそれをFC1を基軸に観察してきたのですが、その同じ正解クラスでも無限に出力パターンはあるけれども、それらを線型結合ですることで必ず一つの答えに導くということを行ってることがわかります。これはある意味モデルのロバスト性を高めるために必要で、必ず一つの出力パターンになる必要はないっていうのも面白いです。
これは、
モデルは「正解クラスに属するための唯一のパターン」を学習するのではなく、
正解クラスと相関のある複数のパターン（manifold）を学習する。
よって同じ正解クラスでも、入力の揺らぎ（位置・ノイズ）によって
どの特徴を使うかが変わっても問題なく分類が成立する。
とまとめることができるかと。