手探りしてみる CV/ ML/ NN: 23日目 Flow Matchingを理解しようとしてみた1

Flow Matching：ノイズからデータへの「まっすぐな道」を理解する

はじめに

Flow Matchingは、ノイズから画像を生成する新しいアプローチです。Diffusion Modelと似ていますが、よりシンプルで高速な仕組みを持っています。

今回は、Flow Matchingの核心的なアイデアを、数式と直感の両面から深く掘り下げていきます。

目次

1. Flow Matchingの核心：分布とは何か
2. 画像を「点」として捉える
3. 「移動」の本当の意味
4. シンプルな美しさ：x - x₀という引き算
5. 速度ベクトルと距離の関係
6. 常微分方程式と積分：理論の基礎
7. 学習のメカニズム
8. 実装：2D点群でのFlow Matching
9. なぜ最短距離にならないのか
10. まとめと次回予告

---

分布とは何か

単なる統計ではない

Flow Matchingを理解する上で、まず「分布」という言葉の意味を正しく捉える必要があります。

よく「画像のRGB値の分布」と聞くと、「赤が20%、青が10%...」といった単純な統計量をイメージしがちです。しかし、Flow Matchingが扱う分布はそうではありません。

同時確率分布という考え方

Flow Matchingが扱うのは、**同時確率分布（Joint Probability Distribution）**です。

64×64ピクセルのRGB画像を例にとると：

• 次元数: 64 × 64 × 3 = 12,288次元
• これら12,288個の値がすべて連携して特定のパターンを成す -> つまりこれ画像そのものだけど

単なる統計: 各ピクセルの色がバラバラに独立（砂嵐になる可能性）
同時確率分布: 「この位置にこの色、隣にこの色」という配置のルールを含む

この「12,288次元がすべて連携した一つの巨大な同時確率の山」を目指して、ノイズから点を移動させるのがFlow Matchingです。

---

画像を「ある点を示すベクトル」として捉える

フラット化の概念

64×64ピクセルのフルカラー画像は、以下のように扱われます：

# 画像の構造
[
    左上のピクセルの (R,G,B),
    その隣のピクセルの (R,G,B),
    ...(中略)...,
    右下のピクセルの (R,G,B)
]

これらをすべて繋げた12,288次元のベクトルが、高次元空間における「1つの点」になります。

画像 = 高次元空間の1点

• 入力時: 画像（縦 × 横 × 色）をフラット化して、高次元空間の「1点」にする
• 学習時: その「点」が、ノイズの状態から画像の状態へどう動くべきか（ベクトル場）を計算
• 生成時: ベクトル場に従って、その「点」を動かしていく

このように、Flow Matchingは「画像全体という1つの点」を、ノイズの海からデータの塊へと導くルートを学習します。

---

「移動」の意味

物理的な移動ではない

「点が移動する」と聞くと、ピクセルが画面上を物理的に動くイメージを持つかもしれません。しかし、実際は違います。

Flow Matchingにおける「移動」とは、12,288次元のベクトルの各要素の値が変化することを、数学的に表現したものです。

2つの視点

物理的な視点: 12,288個の箱（次元）の中身（RGB値）が少しずつ書き換わる

数学的な視点: 12,288次元空間の中にある「1つの点」が、その座標を変える

例えば、12,288次元ベクトルのうち、ある1つの次元（左上の赤色成分）の値が 0.1 から 0.5 に増えたなら、それは12,288次元空間において、その軸の方向に「移動」したとみなせます。

Flow Matchingが学習する「ベクトル場」とは、「各次元の値をどれくらい増減させるべきか」という指示書の束のことです。

---

x - x₀という引き算

究極にシンプルな正解

Flow Matchingの最もシンプルで本質的な特徴は、ただの引き算を学習しているという点です。

あるノイズ x₀ から 正解画像 x₁ への最短距離の方向は：

v = x₁ - x₀

この単純な引き算が、Flow Matchingの 「直線の滑り台」 を定義します。

学習時は答えがわかっている

Flow Matchingの学習時には、以下のペアが与えられます：

• x₀: ノイズ（スタート地点）
• x₁: データ（ゴール地点）

このとき、どの地点 t にいても、進むべき方向（速度）は常に一定の x₁ - x₀ であれば、一番効率よくゴールに着けます。

だから、学習の正解（教師信号）はただの引き算になるのです。

---

速度ベクトルと距離の関係

「方向」だけでなく「大きさ」も出る

Flow Matchingのネットワークが出力するのは、**方向だけではなく、速度（方向 + 大きさ）**です。

多くの解説で「方向」と言われるため混乱しやすいですが、実際にはベクトルの大きさ（強さ）も含まれています。

なぜ大きさが正しく出るのか

学習時、モデルには引き算の結果 x₁ - x₀ を正解として与えています。

• もし x₁ と x₀ の距離が遠ければ、この引き算の結果（ベクトル）は大きくなります
• もし近ければ、この結果は小さくなります

モデルはこの「引き算の答え」そのものを予測するように学習するため、推論時にも、現在の x_t と t を見て、**「t=1 でゴールにたどり着くために必要な、適切な大きさのベクトル」**を出力できます。

時間を固定して速度を調整

Flow Matchingでは、 「1秒（t が 0 から 1 になる間）で必ずゴールに到着する」 というルールがあります。

距離が長いペア (x₀, x₁): 1秒で着くために、速い速度ベクトルを学習
距離が短いペア (x₀, x₁): 1秒で着くために、ゆっくりした速度ベクトルを学習

「距離が違っても、到着時間（t=1）を固定することで、必要な『速度』を逆算させている」というのが、Flow Matchingの賢い設計です。

サンプラーとの役割分担

# ネットワークが出すもの
v = model(x_t, t, condition)  # 速度ベクトル（向きと大きさ）

# サンプラーがやること
x_next = x_t + v * Δt  # 時間の刻みを掛けて移動

• ネットワーク: 「今、この速さ（大きさ）で進め」という速度ベクトルを計算
• サンプラー: 「でも今は Δt 秒分しか進まないよ」と時間を短く刻む

この二人三脚により、最初はぼんやり、最後はくっきりと画像が組み上がります。
ノイズを見ていきなり出たベクトルで正解に1stepで一気に辿り着けるわけはないので、方向と大きさとstep数を決めてそれらを元にどれだけ進むかを決めるのです。そうするとノイズから一歩分だけ正解画像に近づいたものが手に入るので、次のステップではこれをモデルにfeedします、といった具合に少しずつ進んでいく。

---

常微分方程式と積分：理論の基礎

ODEとは「ルール」のこと

「常微分方程式（ODE）」と聞くと難しそうですが、今の文脈では非常にシンプルです。

**「今の場所と時間から、次の瞬間の行き先を決めるルール」**のことです。

カーナビのたとえ

車を運転していると想像してください：

今の状態: 現在の座標 x（どこにいるか）と、時刻 t
ルール（ODE）: カーナビが「今、時速60kmで北へ進め」と指示
結果: その指示に従って走ると、位置 x が時間とともに変化

数式で書くと：

dx/dt = v(x, t)

• 左辺: 位置の変化（速度、つまり傾き）
• 右辺: ネットワークが決める「指示」

「微分」と「積分」のつながり

Flow Matchingが学習しているのは、各地点での**「傾き（微分）」**です。

生成時は、その傾きに従って少しずつ進みます。これは数学で言うところの**「常微分方程式（ODE）を数値的に解く」という作業で、実質的には「積分」**を行っています。

微分: 道のりから「速度」を割り出す
積分: 速度から「道のり」を割り出す

「積分」という見方が最もわかりやすい

「各地点での小さな速度（微分）を、コツコツと積み上げていく（積分）ことで、最終的な道のり（画像）にたどり着く」

このイメージができると、Flow Matchingの全体像がすっきりします。

なぜ「Flow Matching」という名前？

「Flow（流れ）」とは、点が移動していく軌跡のことです。その「流れの傾き」を、理想の傾き（直線）に 「Matching（一致）」 させるように学習するから、Flow Matchingと呼ばれます。

---

学習のメカニズム

直線補間：x_t = (1-t)x₀ + tx₁

学習時、モデルには「旅の途中」の画像を見せる必要があります。これを t をパラメータとした式で定義します。

x_t = (1 - t) * x₀ + t * x₁

• t=0 のとき: x₀ （完全なノイズ）
• t=1 のとき: x₁ （完全な画像）
• t=0.5 のとき: x₀ と x₁ が半分ずつ混ざった状態

この式があるおかげで、どんな中途半端な時刻 t でも、微分可能な形で「今の場所 x_t」を瞬時に作り出せます。

速度ベクトルの定義

x_t の式を、時間 t で微分してみます：

d/dt x_t = d/dt ((1-t)x₀ + tx₁) = x₁ - x₀

この微分した結果、つまり**「直線の傾き」が x₁ - x₀ になる**ことが数学的に導かれます。

Loss関数

モデルの学習目標は、この微分値に一致させることなので、Loss関数はこうなります：

Loss = ||v_θ(x_t, t) - (x₁ - x₀)||²

これは「ネットワーク v_θ が、引き算の答えを正しく予測できるか」を評価します。

学習のステップ

1. データセットからノイズ x₀ と画像 x₁ をサンプリング
2. ランダムな時刻 t（0〜1）を選ぶ
3. 中間地点 x_t = (1-t)x₀ + tx₁ を計算
4. モデルに (x_t, t) を入力して速度ベクトル v_pred を予測
5. 正解 v_target = x₁ - x₀ とのMSE Lossを計算
6. バックプロパゲーションでモデルを更新

これを何億回も繰り返すと、モデルは「どのノイズから出発しても、画像らしいデータに辿り着く道筋」をマスターします。

時間 t のサンプリング戦略

基本的には、0〜1の間から一様にランダムに選びます。

しかし、最新のモデル（Flux.1など）では、Time Shiftという技術を使い、特定の時間帯を重点的に学習させます：

t≈0（初期）: 大まかな構図を学ぶ
t≈0.5（中期）: 砂嵐から物体が現れる瞬間（最も難しい）
t≈1（終盤）: 質感などの細かい仕上げ

「画像が化ける瞬間」を重点的に練習させることで、モデルの性能を最大限に引き出します。

---

実装：2D点群でのFlow Matching

なぜ2D点群なのか

Flow Matchingの理論を体験するには、2次元の点群が最適です：

• 画像（12,288次元）より圧倒的に軽い
• 視覚的に「スルスルと点が動く様子」を確認できる
• 数分で学習完了

チェッカーボード問題

有名なデモでは、ランダムなノイズの点群が、市松模様（チェッカーボード）の形に整列します。

これは、Flow Matchingが「複雑な構造（チェッカー模様）」を「最短距離（直線）」で学習できることを証明しています。

実装の骨組み

import torch
import torch.nn as nn

# モデル: 入力(x, y, t)の3次元 → 出力(vx, vy)の2次元
class FlowModel(nn.Module):
    def __init__(self, hidden_dim=128):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(3, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, 2)  # 速度ベクトル
        )

    def forward(self, x, t):
        # x: [batch, 2], t: [batch, 1]
        input_data = torch.cat([x, t], dim=-1)  # [batch, 3]
        return self.net(input_data)

# 学習の1ステップ
def train_step(model, optimizer, x0, x1):
    optimizer.zero_grad()

    # ランダムな時刻をサンプリング
    batch_size = x0.shape[0]
    t = torch.rand(batch_size, 1)

    # 中間地点を計算
    x_t = (1 - t) * x0 + t * x1

    # 速度ベクトルの正解
    v_target = x1 - x0

    # モデルの予測
    v_pred = model(x_t, t)

    # Loss計算
    loss = nn.functional.mse_loss(v_pred, v_target)

    # 更新
    loss.backward()
    optimizer.step()

    return loss.item()

# 生成（推論）
def generate(model, num_steps=100, num_points=128):
    # ノイズからスタート
    x = torch.randn(num_points, 2)

    # ODEを解く（Euler法）
    dt = 1.0 / num_steps
    for step in range(num_steps):
        t = torch.full((num_points, 1), step * dt)

        with torch.no_grad():
            v = model(x, t)

        # 1ステップ進む
        x = x + v * dt

    return x

実際の学習

# チェッカーボードのターゲット座標を準備
# （省略: 黒マスの座標をサンプリング）

model = FlowModel()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)

for epoch in range(10000):
    # ノイズとターゲットをサンプリング
    x0 = torch.randn(128, 2)
    x1 = sample_checkerboard_points(128)

    loss = train_step(model, optimizer, x0, x1)

    if epoch % 1000 == 0:
        print(f"Epoch {epoch}, Loss: {loss:.4f}")

# 生成
points = generate(model)
# → points が市松模様を形成！

画像への拡張

チェッカーボードではなく、白黒画像をターゲットにすることも可能です：

# 画像の白い部分の座標をサンプリング
def sample_from_image(image, num_points):
    # 画像の明るさを重みとして、ランダムに(x, y)を抽出
    ...

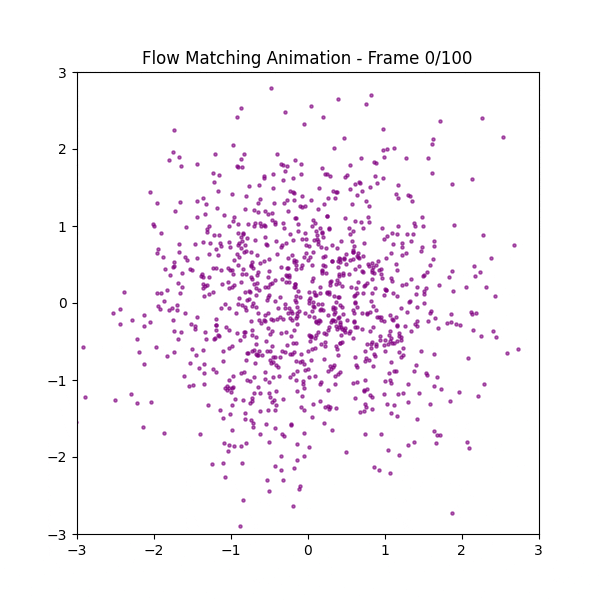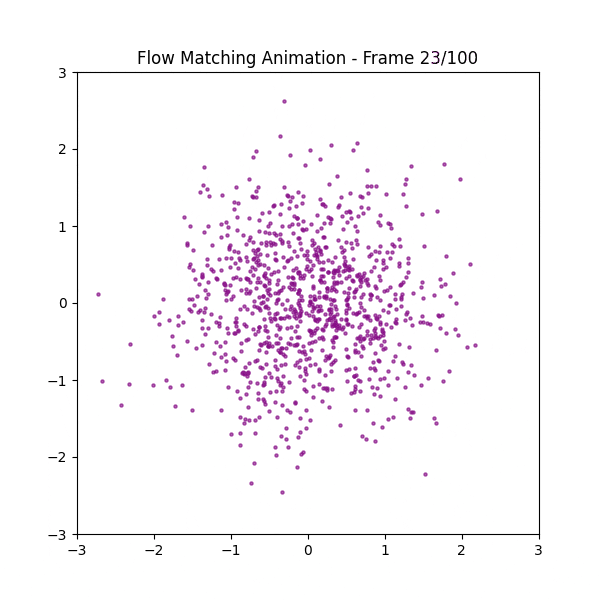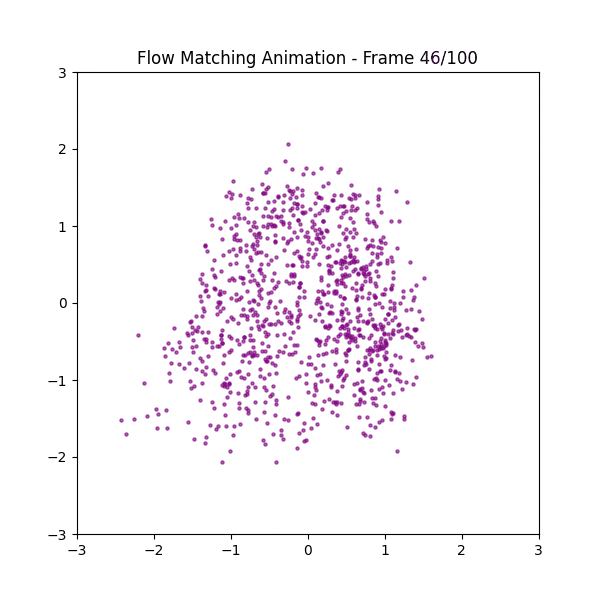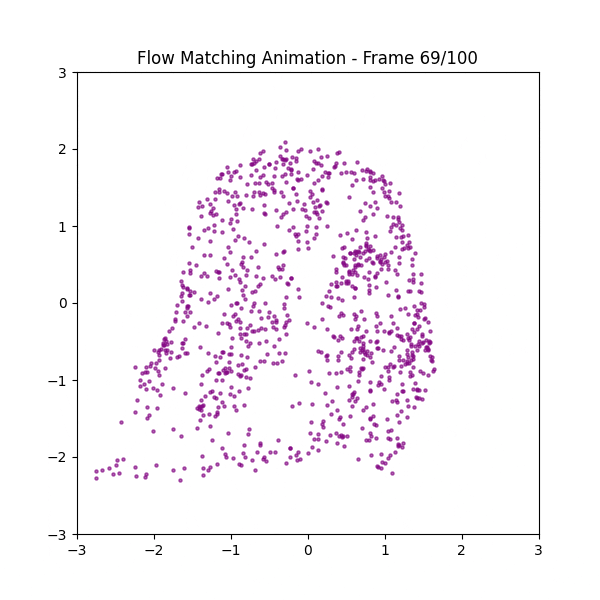
フクロウの画像を点描してその点群の座標を学習させてみた

---

なぜ最短距離にならないのか

理想と現実のギャップ

Flow Matchingは「直線を学習している」と言いましたが、実際のデモ動画を見ると、点の軌跡が微妙に曲がっていることに気づきます。

なぜ最短距離（直線）にならないのでしょうか？

理由1：ネットワークは「平均」を答えてしまう

学習中、モデルは同じノイズ x₀ に対して、いろいろな目的地 x₁ への直線ベクトルを教わります。

ある時は「右上」へ行けと言われ
ある時は「右下」へ行けと言われる

すると、初期段階（t が小さい時）のモデルは、自信がないのでその**平均（つまり真東）**を向いてしまいます。

しばらく進むと、「あ、今の位置からすると、正解は右下だったんだな」と確信が持てるようになり、そこでグイッと舵を切ります。

この**「確信が高まるにつれての進路修正」**が、カーブ（遠回り）として見えるのです。

理由2：最適輸送（Optimal Transport）の問題

「どのノイズをどのゴールに運ぶか」という組み合わせが、数学的に最も効率的（全体として最短）になるように学習させるのが理想です。

しかし、ランダムにペアを作って学習させると、**「交差するルート」**が発生してしまいます。

Aのノイズが遠くのBのゴールへ
Bのノイズが遠くのAのゴールへ

このような無駄な指示をモデルが学習してしまうと、推論時に「あっちへ行こうか、こっちへ行こうか」という迷いが生じ、最短距離から外れます。

理由3：ネットワークの表現力の限界

ニューラルネットワークは「完璧な直線」を完璧に記憶できるわけではありません。数学的には x₁ - x₀ という定数を学習させていますが、ネットワークがそれを近似する際にどうしても**「歪み」**が生じます。

その歪みが、あのスルスルと動く時の「独特なうねり」となって現れます。

「でも、それがいい」

面白いことに、この「最短ではない、少しゆらぎのあるルート」こそが、AI生成画像の**「多様性」や「自然さ」**を生んでいたりします。

完璧に最短なら: 計算は速いが、機械的な変化
実際: 迷いながら、周囲と相談しながら徐々に形を成す

全体として調和の取れた画像が組み上がるのです。

---

まとめ

Flow Matchingの本質

• 分布: 単なる統計ではなく、12,288次元すべてが連携した同時確率分布
• 画像: フラット化して高次元空間の1点として扱う
• 移動: ピクセルの物理的移動ではなく、ベクトルの値の変化
• 引き算: x₁ - x₀ という究極にシンプルな正解
• 速度: 方向だけでなく、大きさ（速さ）も出力
• 時間: t=1で必ず到着するように速度を調整
• ODE: 微分（傾き）を学習し、積分（生成）で画像を作る
• 直線補間: x_t = (1-t)x₀ + tx₁ という学習のスケジューラー

拡散モデルとの違い

項目	拡散モデル	Flow Matching
学習の方向	x → x₀（逆方向）	x₀ → x₁（順方向）
経路	カーブ（複雑）	直線（シンプル）
数式	複雑な√付き	単純な線形補間
ステップ数	多い（100〜1000）	少ない（10〜50）

---

参考

• Flow Matching論文: Flow Matching for Generative Modeling
• Rectified Flow: Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow