はじめに
今回は、XGBoostなどの機械学習において根幹を成している理論、Gradient Tree Boostingについて理解してみる。
XGBoostはKaggleなどのコンペで愛用されている手法だが、その理論を知らずに頼るのはなんか気持ち悪いし、サイエンスではない。また、理論を知ってこそ、それを活用することができると信じているので、一度ここでまとめて見たい。急がば回れである。
ただし、あくまでこれは私が理解している限りを記述したメモ書きであることに注意していただきたい。
なお、以下の内容は、XGBoostの論文のSection2を参考にしている。
Gradient Tree Boosting
Gradient Tree Boostingはアンサンブル学習の一つである。
そもそも機械学習の目標は、汎化能力が高い学習器をデータから構築することであるが、その汎化能力を高めるためには以下2つの方針が考えられる:
- 単一の学習器の精度を向上させ、強学習器を構築する
- 複数の弱学習器を用意し、それらの予測結果を統合することで強学習器を構築する
アンサンブル学習とはまさに後者の方針をとった機械学習である。
また、アンサンブル学習には主に以下2種類の手法が存在する:
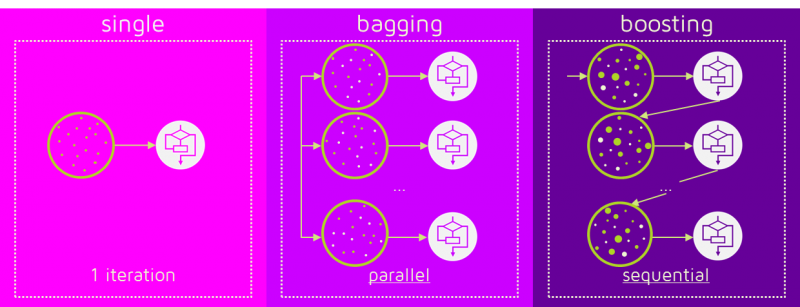
- Bagging:様々な弱学習器を独立(parallel)に作り、それらの予測結果を統合する手法
- Boosting:様々な弱学習器を逐次的(sequential)に作り、それらの予測結果を統合する手法
前者にはRandom Forestなどの手法がある一方、後者にはAdaBoostやGradient Boostingなどの手法が存在する。
BaggingとBoostingのイメージを示したものが下図である。
(引用元) : https://quantdare.com/what-is-the-difference-between-bagging-and-boosting/
今回考えるGradient Tree Boostingとは、上記のRandom ForestとGradient Boostingを組み合わせたようなものである。
Tree Ensemble Model
さて、ここではTree Ensemble Modelについて記述する。
今、$n$個のサンプル、$m$個の特徴量(カラムなど)を持つデータセット
$
\mathcal{D} = \{(\boldsymbol{x}_i, y_i)\} \quad (|\mathcal{D}| = n, \boldsymbol{x}_i \in \mathbb{R}^m, y_i \in \mathbb{R})$
を用いて回帰を行うとする。ただし、$\boldsymbol{x}_i$は説明変数、$y_i$は目的変数を表している。また、数式中の太字はベクトルを意味する。
今、$K$個のTreeからなるモデルを考えた時、予測値$\hat{y}_i$は
\hat{y}_i = \phi(\boldsymbol{x}_i) = \sum_{k=1}^{K} f_k(\boldsymbol{x}_k)\quad ( f_k\in\mathcal{F})\\
where \mathcal{F} = \{f(\boldsymbol{x}) = w_{q(\boldsymbol{x})}\}\quad (q:\mathbb{R}^m\rightarrow T, w\in\mathbb{R}^T)
で記述される。
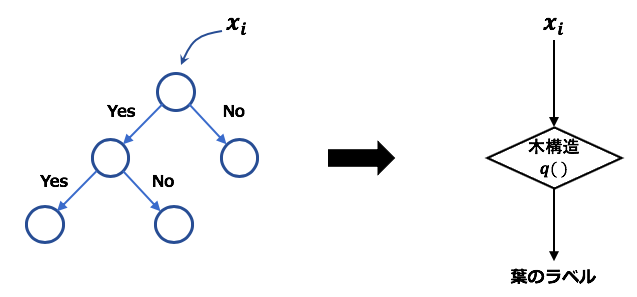
ここで、$\mathcal{F}$は回帰木空間(CART)と呼ばれ、葉のウェイト$w$と葉の数$T$が定義される。ただし、葉の数$T$は$K$個のTreeごとに定められた値ではなく、それぞれ共通した値を持っており、XGBoostではmax_depthというパラメータで与える必要がある。
また、$q(\boldsymbol{x})$は木構造を表しており、大雑把にいうと、入力値がモデルによってどの葉に分けられたかをインデックスで返す関数と解釈できる。
つまり、上式の意味することは、「$q$で決定される木構造によって入力値がそれぞれの葉に分けられる。そしてその葉におけるウェイトを$K$個のTreeで足し合わせ、その値を予測値$\hat{y}_i$として出力する」ということである。
Regularized Learning Objective
モデルの最適化にあたって、モデルの評価を行う関数が必要である。ニューラルネットワークでは損失関数がこれに値する。ここでは、以下の式で表される関数を最小化することで、モデルの最適化を行う:
L(\phi)=\sum_i l(\hat{y}_i, y_i)+\sum_k\Omega(f_k)\\
where \Omega(f) = \gamma T + \frac{\lambda}{2}||w||^2
上式右辺第一項の$l(\hat{y}_i, y_i)$は予測値$\hat{y}_i$と正解値$y_i$の差分を計算する凸損失関数である。
上式右辺第二項の$\Omega(f)$は正則化項であり、$||w||$はL2ノルムである。正則化項の寄与についてはリッジ回帰の記事を参照してほしい。ここでは$\gamma T$が加わっており、葉を多くする、つまりモデルを複雑化することに対するペナルティを付与している。
$\gamma, \lambda$はハイパーパラメータである。
Gradient Tree Boosting
ここからこのTreeをBoostするわけだが、前節の式では関数$f$がパラメータとして最適化を行うような記述がされている。しかし、いわゆるユークリッド空間での最適化(勾配降下法など)による最適化は不可能である。
そこで、iterationごとに関数を付加していく形で最適化を行う。
今、$t$番目のiterationにおける$i$番目のインスタンスを持つ予測値を$\hat{y}_i$と表現すると、$t$番目のiterationにおける目的関数$L^{(t)}$は
L^{(t)} = \sum_{i=1}^n l\left(y_i, \hat{y}_i^{(t-1)} + f_t(\boldsymbol{x}_i)\right) + \Omega(f_t)
と記述できる。この式の意味することは、「$t-1$番目のiterationにおけるモデルに対して$f_t$を付加することで、目的関数を減少させるという試み」である。
ここで、上式右辺第一項を二次までで展開すると
\begin{eqnarray}
L^{(t)} &\simeq& \sum_{i=1}^n\left[l\left(y_i, \hat{y}_i^{(t-1)}\right) + \frac{\partial l}{\partial\hat{y}_i^{(t-1)}}f_t(\boldsymbol{x}_i) + \frac{1}{2}\frac{\partial^2 l}{\partial{\hat{y}_i^{(t-1)}}^2}f_t^2(\boldsymbol{x}_i)\right] + \Omega(f_t) \\
&=& \sum_{i=1}^n\left[l\left(y_i, \hat{y}_i^{(t-1)}\right) + g_i f_t(\boldsymbol{x}_i) + \frac{1}{2}h_i f_t^2(\boldsymbol{x}_i)\right] + \Omega(f_t)
\end{eqnarray}
となる。ただし、
\begin{eqnarray}
g_i &\equiv& \frac{\partial l}{\partial\hat{y}_i^{(t-1)}}\\
h_i &\equiv& \frac{\partial^2 l}{\partial{\hat{y}_i^{(t-1)}}^2}
\end{eqnarray}
とした。定数項を除くと
\tilde{L}^{(t)} = \sum_{n=1}^n\left[g_i f_t(\boldsymbol{x}_i) + \frac{1}{2}h_i f_t^2(\boldsymbol{x}_i)\right] + \Omega(f_t)
となる。
ここで、$I_j = \{i|q(\boldsymbol{x}_i)=j\}$を定義する。これは、モデルによって$j$番目の葉に分けられた、$i$番目のデータのインデックスによる集合を表す。$I_j$を用いると、
\begin{eqnarray}
\tilde{L}^{(t)} &=& \sum_{n=1}^n\left[g_i f_t(\boldsymbol{x}_i) + \frac{1}{2}h_i f_t^2(\boldsymbol{x}_i)\right] + \gamma T + \frac{\lambda}{2}\sum_{j=1}^Tw_j^2 \\
&=& \sum_{j=1}^T\left[\left(\sum_{i\in I_j}g_i\right)w_j + \frac{1}{2}\left(\sum_{i\in I_j}h_i + \lambda\right)w_j^2\right] + \gamma T
\end{eqnarray}
と変形できる。つまり、各々の葉におけるスコアの総和として書くことができた。
ただし、上式では$\mathcal{F}$の定義を用いている。
さて、$w_j$をパラメータとしたこの関数に対して、最小値を満たす時の条件は
\frac{\partial\tilde{L}^{(t)}}{\partial w_j} = 0
であり、この時の$w_j$を$w_j^*$とすると、
\left(\sum_{i\in I_j}g_i + \frac{1}{2}\sum_{i \in I_j}(h_iw_j^* + \lambda)\right) + \frac{1}{2}\sum_{i \in I_j}(h_iw_j^* + \lambda) = 0 \\
\Leftrightarrow w_j^* = -\frac{\sum_{i\in I_j}g_i}{\sum_{i \in I_j}h_iw_j^* + \lambda}
と、$w_j$の最適値を求めることができる。この$w_j^*$を目的関数の式に代入すれば、木構造$q$における最適な目的関数$\tilde{L}^{(t)}(q)$は
\tilde{L}^{(t)}(q) = -\frac{1}{2}\sum_{j=1}^T\frac{\left(\sum_{i\in I_j}g_i\right)^2}{\sum_{i \in I_j}h_iw_j^* + \lambda} + \gamma T
と求められる。
通常、モデルの最適化では、single leafから始まり、iterationごとにtreeに枝を追加していくという手法をとる。
ここで、枝分かれ後のinstance setsをそれぞれ$I_L, I_R$と定義し、枝分かれ前のinstance sets $I$に対して、$I = I_L \cup I_R$が成り立つとする。すると、枝分かれによる目的関数の減分$L_{split}$は
\begin{eqnarray}
L_{split} &=& L_{before} - L_{after} \\
&=& \left\{-\frac{1}{2}\frac{\left(\sum_{i\in I}g_i\right)^2}{\sum_{i \in I}h_iw_j^* + \lambda} + \gamma\right\} - \left\{\left(-\frac{1}{2}\frac{\left(\sum_{i\in I_L}g_i\right)^2}{\sum_{i \in I_L}h_iw_j^* + \lambda} + \gamma\right) + \left(-\frac{1}{2}\frac{\left(\sum_{i\in I_R}g_i\right)^2}{\sum_{i \in I_R}h_iw_j^* + \lambda} + \gamma\right)\right\} \\
&=& \frac{1}{2}\left[\frac{\left(\sum_{i\in I_L}g_i\right)^2}{\sum_{i \in I_L}h_iw_j^* + \lambda} + \frac{\left(\sum_{i\in I_R}g_i\right)^2}{\sum_{i \in I_R}h_iw_j^* + \lambda} - \frac{\left(\sum_{i\in I}g_i\right)^2}{\sum_{i \in I}h_iw_j^* + \lambda}\right] - \gamma
\end{eqnarray}
と計算できる。つまり、この関数を計算することによって、対象の分岐を行うか否かを判断することができる。
以上のプロセスをiterationごとに行うことによって、Boostingによるモデルの最適化を行うことができる。
実際にはそれぞれのインスタンスに対する$g$と$h$の値を保持しておけば良い。
終わりに
XGBoostの理論であるGradient Tree Boostingを数式的に読み解いてみたがいかがだろうか。
皆さんも精度の向上でキモチヨクなる前に、式を追ってキモチヨクなろう()
解釈の間違いなどがあれば、ぜひ指摘してくださるとタスカル。
参考
- XGBoost元論文 https://arxiv.org/abs/1603.02754
- https://www.st-hakky-blog.com/entry/2017/07/28/214518
- https://quantdare.com/what-is-the-difference-between-bagging-and-boosting/
参考にさせていただきました。ありがとうございました。