データ解析のための統計モデリング入門 GLMの応用範囲をひろげる

ロジスティック回帰やポアソン回帰のオフセット項わざ，正規分布やガンマ分布を使うGLMを扱う．

さまざまな種類のデータを応用できるGLM

確率分布・リンク関数・線形予測子の組み合わせによって，GLMで様々なタイプのデータを表現できる．

Python内でのGLM構築に使える確率分布の一部
乱数生成はscipy.stats.X，glm()のfamilyはstatsmodels.api.families.Xで指定する．

| 　|確率分布 |乱数生成|glm()のfamily指定|よく使うリンク関数|
|:-:|:-:|:-:|:-:|:-:|:-:|
|（離散）|二項分布|binom.rvs()|Binomial()|logit|
|　| ポアソン分布 | poisson.rvs() | Poisson() | log |
|　|負の二項分布|nbinom.rvs()|NegativeGaussian()|log|
|（連続）| ガンマ分布 | gamma.rvs()|Ganma()| log?|
|　| 正規分布 | norm.rvs() | Gaussian() | identity|

二項分布を使ったGLM

二項分布は，上限のあるカウントデータ（応答変数が$y \in \{ 0, 1, 2, \dots, N \} $）のときに用いる．

N個体の実験対象に同じ処理をしたら，$y$個体で反応が陽性，$N-y$個体では陰性だった

今回の例題は，

「ある架空植物の個体$i$それぞれにおいて，$N_i$個の観察種子のうち生きていて発芽能力があるものは$y_i$個，死んだ種子は$N_i-y_i$個」

という観測データで，全部で100個体の植物を調べたとする．
※なお，観察種子数$N_i$はどの個体でも8個とする．

応答変数について

応答変数である生存種子数のとりうる値は，$y_i \in \{0, 1, 2, 3, \dots, 8 \}$となり，
全部生存していた場合は$y_i = 8$，全趣旨が死亡していた場合は$y_i=0$となる．

「ある個体$i$から得られた一個の種子が生きている確率」を$q_i$とする．

説明変数について

個体の大きさを表す体サイズ$x_i$によって，生存確率$q_i$が上下する．
また，全100個体のうち50個体（$i \in \{1, 2, \dots, 50 \}$）は無処理（$f_i = C$）,
残りの50個体（$i \in \{ 51, 52, \dots, 100 \}$）は施肥処理（$f_i = T$）とする．

>>> import pandas
>>> import matplotlib.pyplot as plt
>>> d = pandas.read_csv("data4a.csv")
>>> d.describe()
         N           y           x
count  100  100.000000  100.000000
mean     8    5.080000    9.967200
std      0    2.743882    1.088954
min      8    0.000000    7.660000
25%      8    3.000000    9.337500
50%      8    6.000000    9.965000
75%      8    8.000000   10.770000
max      8    8.000000   12.440000
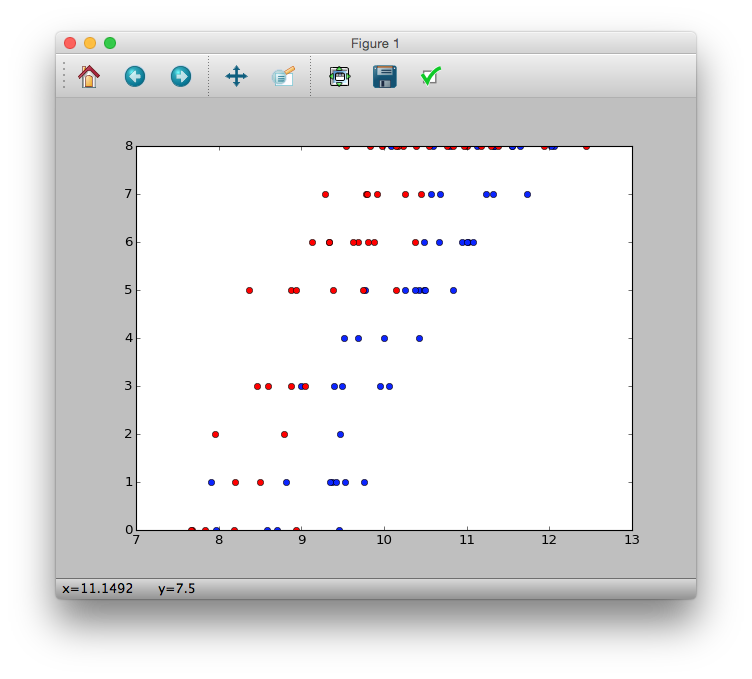
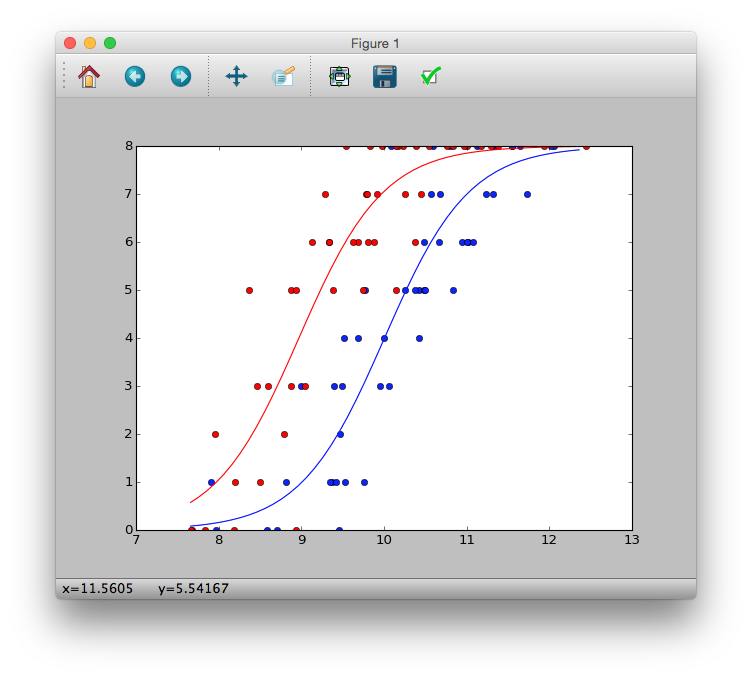
>>> plt.plot(d.x[d.f == 'C'], d.y[d.f == 'C'], 'bo')
>>> plt.plot(d.x[d.f == 'T'], d.y[d.f == 'T'], 'ro')
>>> plt.show()

図からわかることとして

• 体サイズ$x_i$が大きくなると生存種子数$y_i$が多くなるらしい
• 肥料をやると（$f_i=T$）生存種子数$y_i$が多くなるらしい

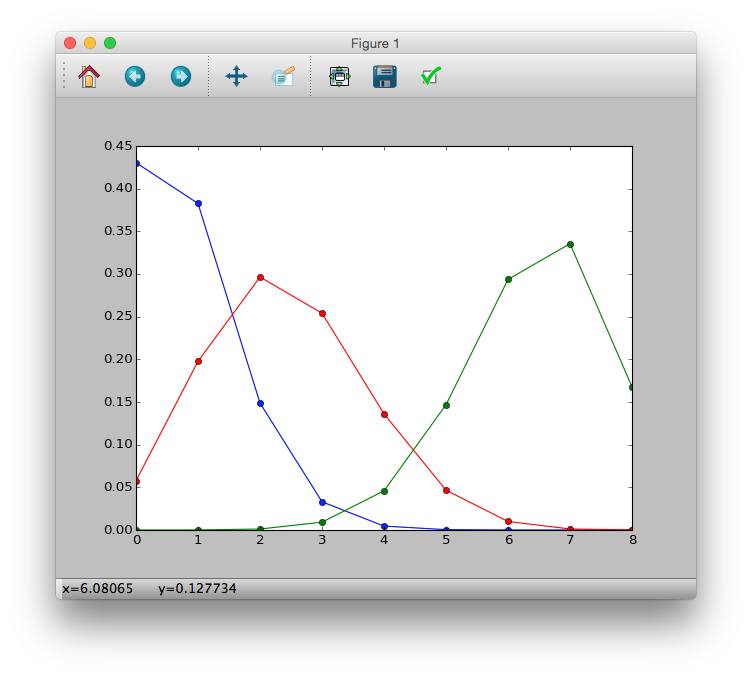
二項分布

p(y|N, q) = \left( \begin{array}{c}
      N \\
      y 
    \end{array}
    \right) q^y (1-q)^{N-y}

>>> import math
>>> p = lambda y, N, q: (math.factorial(N) / (math.factorial(y) * math.factorial(N-y))) * (q ** y) * ((1-q) ** (N-y))
>>> p1 = [p(i, 8, 0.1) for i in y]
>>> p2 = [p(i, 8, 0.3) for i in y]
>>> p3 = [p(i, 8, 0.8) for i in y]
>>> plt.plot(y, p1, 'b-o')
>>> plt.plot(y, p2, 'r-o')
>>> plt.plot(y, p3, 'g-o')
>>> plt.show()

ロジスティック回帰とロジットリンク関数

ロジスティック回帰では，

• 確率分布：二項分布
• リンク関数：ロジットリンク関数（logit link function）

を用いる．

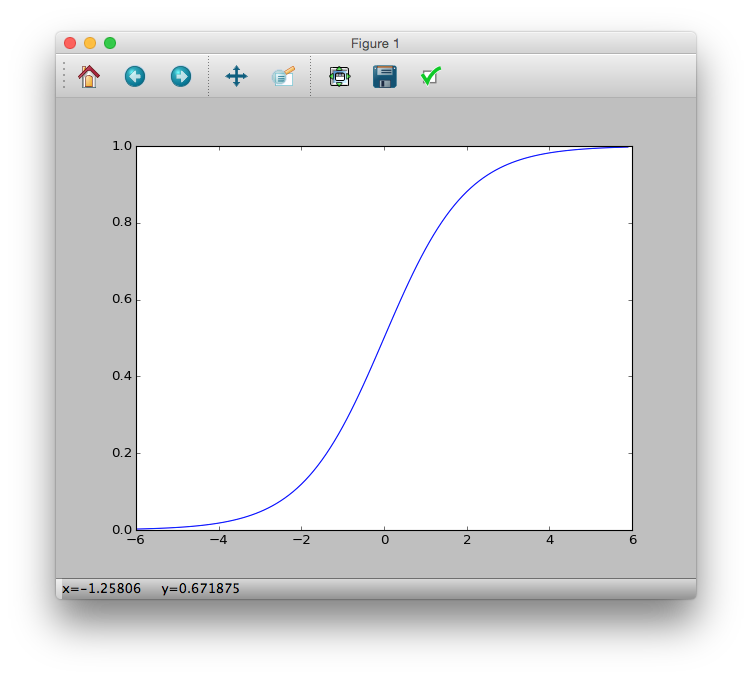
ロジスティック関数について

q_i = logistic(z_i) = \frac{1}{1+\exp(-z_i)}

と定義され，変数$z_i$は線形予測子$z_i = \beta_1 + \beta_2 x_1 + \dots$である．

>>> logistic = lambda z: 1 / (1 + numpy.exp(-z))
>>> z = numpy.arange(-6, 6, 0.1)
>>> plt.plot(z, logistic(z))
>>> plt.show()

生存確率$q_i$が$z_i$のロジスティック関数であると仮定すると，線形予測子$z_i$がどんな値でも，$0 \leq q_i \leq 1$となる．

生存確率$q_i$が体サイズ$x_i$だけに依存していると仮定すると，線形予測子$z_i=\beta_1 + \beta_2 x_i$となる．

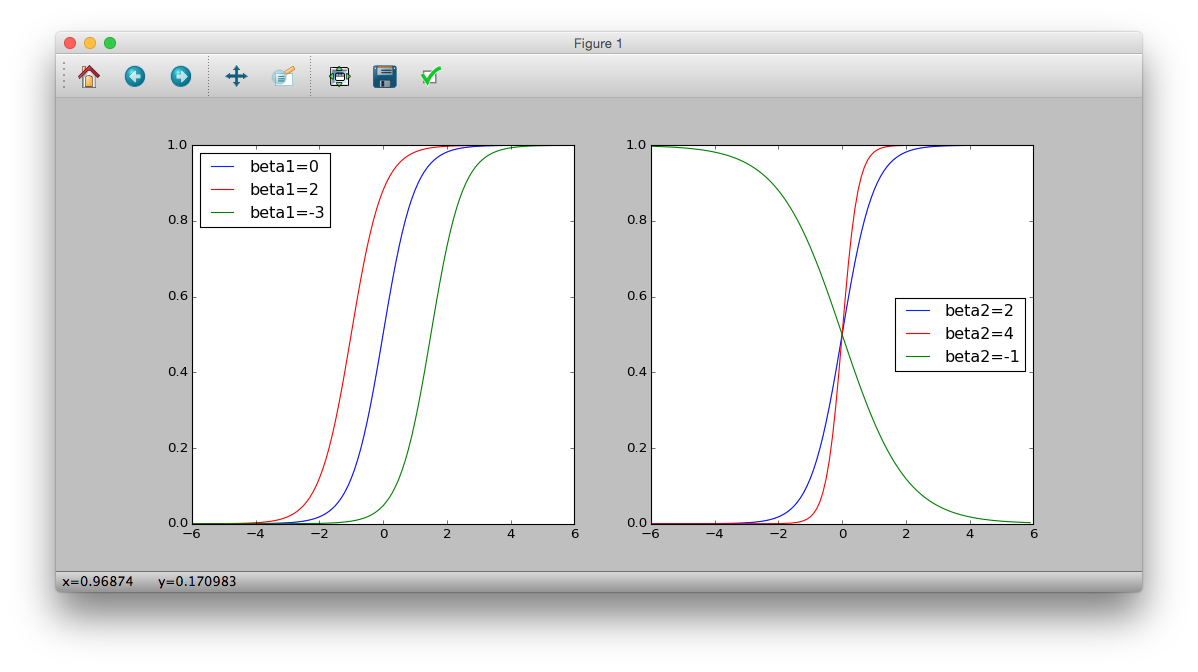
$q_i$と$x_i$が$\beta_1$と$\beta_2$に依存している様子

>>> plt.subplot(121)
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(0 + 2 * x)))
>>> plt.plot(z, logistic(z), 'b-', label='beta1=0')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(2 + 2 * x)))
>>> plt.plot(z, logistic(z), 'r-', label='beta1=2')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(-3 + 2 * x)))
>>> plt.plot(z, logistic(z), 'g-', label='beta1=-3')
>>> plt.legend(loc='middle right')
>>> plt.subplot(122)
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(2 * x)))
>>> plt.plot(z, logistic(z), 'b-', label='beta2=2')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(4 * x)))
>>> plt.plot(z, logistic(z), 'r-', label='beta2=4')
>>> logistic = lambda x: 1 / (1 + numpy.exp(-(-1 * x)))
>>> plt.plot(z, logistic(z), 'g-', label='beta2=-1')
>>> plt.legend(loc='middle right')
>>> plt.show()

ロジット関数

ロジスティック関数を変形する．

\begin{eqnarray}
q_i &=& \frac{1}{1+\exp(-z_i)} \\
q_i + q_i \exp(-z_i) &=& 1 \\
1 - q_i &=& q_i \exp (-z_i)\\
\frac{1 - q_i}{q_i} &=& \exp (-z_i) \\
\log \frac{1 - q_i}{q_i} &=& -z_i \\
\log \frac{q_i}{1 - q_i} &=& z_i
\end{eqnarray}

左辺をロジット関数とよぶ．

logit(q_i) = \log \frac{q_i}{1 - q_i}

※ロジット関数はロジスティック関数の逆関数

パラメータ推定

生存確率$q_i$のもとでの(対数)尤度を最大化させる．

\begin{eqnarray}
L(q) &=& \prod_i p(y_i | N_i, q_i) \\
&=& \prod_i \left( \begin{array}{c}
      N_i \\
      y_i 
    \end{array}
    \right)q_i^{y_i}(1-q_i)^{N_i-y_i} \\
L(\{\beta_1, \beta_2, \beta_3\}) &=& \prod_i \left( \begin{array}{c}
      N_i \\
      y_i 
    \end{array}
    \right)q_i^{y_i}(1-q_i)^{N_i-y_i} (\because logit(q_i) = z_i = \beta_1 + \beta_2 x_i + \beta_3 d_i) \\
logL(\{\beta_1, \beta_2, \beta_3\}) &=& \sum_i \log \left\{\left( \begin{array}{c}
      N_i \\
      y_i 
    \end{array}
    \right)q_i^{y_i}(1-q_i)^{N_i-y_i} \right\} \\

logL(\{\beta_1, \beta_2, \beta_3\}) &=& \sum_i \left\{ \log \left( \begin{array}{c}
      N_i \\
      y_i 
    \end{array}
    \right) + \log q_i^{y_i} + \log (1-q_i)^{N_i-y_i} \right\} \\

logL(\{\beta_1, \beta_2, \beta_3\}) &=& \sum_i \left\{ \log \left( \begin{array}{c}
      N_i \\
      y_i 
    \end{array}
    \right) + (y_i)\log q_i + (N_i-y_i)\log (1-q_i) \right\} \\
\end{eqnarray}

>>> import statsmodels.formula.api as smf
>>> import statsmodels.api as sm
>>> import pandas
>>> d = pandas.read_csv("data4a.csv")
# glm(cbind(y, N-y) ~ x + f, data=d, family=binomial)
>>> model = smf.glm('y + I(N-y) ~ x + f', data=d, family=sm.families.Binomial())
>>> fit = model.fit()
>>> fit.summary()
                 Generalized Linear Model Regression Results
==============================================================================
Dep. Variable:      ['y', 'I(N - y)']   No. Observations:                  100
Model:                            GLM   Df Residuals:                       97
Model Family:                Binomial   Df Model:                            2
Link Function:                  logit   Scale:                             1.0
Method:                          IRLS   Log-Likelihood:                -133.11
Date:                Sat, 06 Jun 2015   Deviance:                       123.03
Time:                        12:06:47   Pearson chi2:                     109.
No. Iterations:                     8
==============================================================================
                 coef    std err          z      P>|z|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept    -19.5361      1.414    -13.818      0.000       -22.307   -16.765
f[T.T]         2.0215      0.231      8.740      0.000         1.568     2.475
x              1.9524      0.139     14.059      0.000         1.680     2.225
==============================================================================

オッズについて

（生存する確率）/ (生存しない確率）という比をオッズとよぶ．

\begin{eqnarray}
\frac{q_i}{1-q_i} &=& \exp(線形予測子) \\
&=& \exp(\beta_1 + \beta_2 x_i + \beta_3 f_i) \\
&=& \exp(\beta_1)\exp(\beta_2 x_i)\exp(\beta_3 f_i)
\end{eqnarray}

今回推定した$\{\beta_2, \beta_3 \}$に着目すると

\frac{q_i}{1-q_i} \propto \exp(1.95x_i)\exp(2.02f_i)

と各説明変数と比例関係になる．

体サイズ$x_i$の影響は，

\begin{eqnarray}
\frac{q_i}{1-q_i} &\propto& \exp(1.95(x_i + 1))\exp(2.02f_i) \\
&\propto& \exp(1.95x_i)\exp(1.95)\exp(2.02f_i)
\end{eqnarray}

から$\exp(1.95) \approx 7.03$倍になることがわかる．
同様に施肥効果も$exp(2.02) \approx 7.54$倍になることがわかる．

オッズ比について

要因$X$の効果（$\beta_x=1.95$）を示す．

\begin{eqnarray}
\frac{Xのオッズ}{非Xのオッズ} &=& \frac{\exp(X\bullet非Xの共通部分)\times \exp(1.95 \times 1)}{\exp(X\bullet非Xの共通部分)\times \exp(1.95 \times 0)} \\
&=& exp(1.95) \approx 7.03
\end{eqnarray}

モデル選択

AICによるモデル選択
ロジスティック回帰のネストしているモデルの選択

• 一定モデル（切片のみ）
• xモデル（体サイズのみ）
• fモデル（施肥効果のみ）
• x+fモデル（体サイズ＋施肥効果）

RにはMASS packageのstepAIC()関数が用意されているらしい．
とりあえず前回と同様にすると，x+fモデルが最もAICが低くなり，良いモデルとなる．

交互作用項

体サイズと施肥効果の掛け合わせによる効果を考える．
つまり，

logit(q_i) = \beta_1 + \beta_2 x_i + \beta_3 f_i + \beta_4 x_i f_i

を考える．

# glm(cbind(y, N-y) ~ x * f, data=d, family=binomial)
>>> model = smf.glm('y + I(N-y) ~ x * f', data=d, family=sm.families.Binomial())
>>> model.fit().summary()
                 Generalized Linear Model Regression Results
==============================================================================
Dep. Variable:      ['y', 'I(N - y)']   No. Observations:                  100
Model:                            GLM   Df Residuals:                       96
Model Family:                Binomial   Df Model:                            3
Link Function:                  logit   Scale:                             1.0
Method:                          IRLS   Log-Likelihood:                -132.81
Date:                 土, 06  6 2015   Deviance:                       122.43
Time:                        13:44:31   Pearson chi2:                     13.6
No. Iterations:                     8
==============================================================================
                 coef    std err          z      P>|z|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept    -18.5233      5.335     -3.472      0.001       -28.979    -8.067
f[T.T]        -0.0638      7.647     -0.008      0.993       -15.052    14.924
x              1.8525      0.525      3.529      0.000         0.824     2.881
x:f[T.T]       0.2163      0.792      0.273      0.785        -1.336     1.769
==============================================================================

と今回はAICが上がってしまったため，交互作用はなかったということ．

割算値の統計モデリングはやめる

ロジスティック回帰のメリットの一つに，$(観測データ) / (観測データ)$という割算値を作る必要がない．
割算地は今回の例題でいう「種子の生存確率が何に依存しているか」を知りたいときにつくりがち．

デメリットとして

• 情報が失われる：例として野球の打率．1000打数300安打と100打数30安打は共に3割打者だが，同様に確からしいといえるだろうか？
• 変換された値の分布は？：誤差が入った数量どうしで作られた割算値はどんな確率分布にしたがうのか？

割算値いらずのオフセット項わざ

以下のような架空データを使う

• 森林のあちこちに調査地100箇所を設定した（$i \in \{ 1, 2, \dots, 100\}$）
• 調査地$i$ごとにその面積$A_i$が異なる
• 調査地$i$の「明るさ」$x_i$を測っている
• 調査地$i$における植物個体数$y_i$を記録した
• （解析目的）調査地$i$における植物個体の「人口密度」が「明るさ」$x_i$にどう影響されているか知りたい

面積$A_i$である調査地$i$における人口密度は，

\frac{平均個体数\lambda_i}{A_i} = 人口密度

である．人口密度は正の量だから，指数関数と明るさ$x_i$依存性を組み合わせて，

\begin{eqnarray}
\lambda_i &=& A_i \times 人口密度 \\
&=& A_i \exp(\beta_1 + \beta_2 x_i) \\
&=& \exp(\beta_1 + \beta_2 x_i + \log A_i)
\end{eqnarray}

となり，$z_i=\beta_1 + \beta_2 x_i + \log A_i$を線形予測子とする対数リンク関数・ポアソン分布のGLMになる．

>>> d = pandas.read_csv("data4b.csv")
>>> model = smf.glm('y ~ x', offset=numpy.log(d.A), data=d, family=sm.families.Poisson())
>>> model.fit().summary()
                 Generalized Linear Model Regression Results
==============================================================================
Dep. Variable:                      y   No. Observations:                  100
Model:                            GLM   Df Residuals:                       98
Model Family:                 Poisson   Df Model:                            1
Link Function:                    log   Scale:                             1.0
Method:                          IRLS   Log-Likelihood:                -323.17
Date:                Sat, 06 Jun 2015   Deviance:                       81.608
Time:                        14:45:24   Pearson chi2:                     81.5
No. Iterations:                     7
==============================================================================
                 coef    std err          z      P>|z|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept      0.9731      0.045     21.600      0.000         0.885     1.061
x              1.0383      0.078     13.364      0.000         0.886     1.191
==============================================================================

正規分布とその尤度

連続値のデータを統計モデルで扱うための確率分布．
ガウス分布（Gaussian distribution）と呼ばれることもある．

パラメータは

• 平均値$\mu$：$\pm\infty$の範囲で自由に変化できる．
• 標準偏差$\sigma$：データのばらつきを指定できる．

p(y| \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp \left\{ -\frac{(y-\mu)^2}{2\sigma^2} \right\}

# y <- seq(-5, 5, 0.1)
# plot(y, dnorm(y, mean=0, sd=1), type="l")
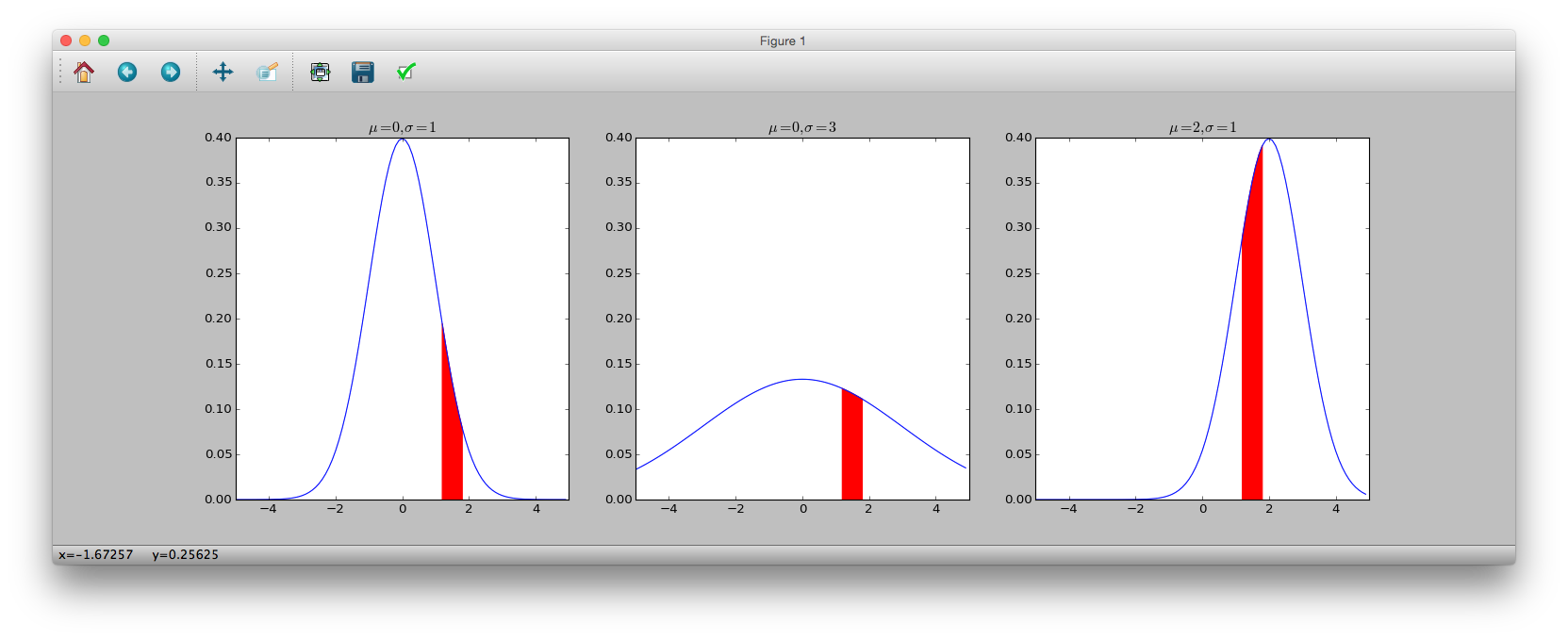
plt.subplot(131)
plt.plot(y, sct.norm.pdf(y, loc=0, scale=1))
plt.title('$\mu=0, \sigma=1$')
plt.subplot(132)
plt.plot(y, sct.norm.pdf(y, loc=0, scale=3))
plt.title('$\mu=0, \sigma=3$')
plt.subplot(133)
plt.plot(y, sct.norm.pdf(y, loc=2, scale=1))
plt.title('$\mu=2, \sigma=1$')
plt.show()

Rでは$\mu$がmean, $\sigma$がsdとなっているが，
pythonでは，$\mu$はloc，$\sigma$はscaleとなっている．

それぞれパラメータを調節したもの．縦軸は確率密度を示している．
赤色で塗られた部分は，$1.2 \leq y \leq 1.8$となる確率の大小が面積として表されている．

正規分布の確率密度関数を$p(y|\mu, \sigma)$とすると，

$p(1.2 \leq y \leq 1.8| \mu, \sigma) = \int_{1.2}^{1.8}p(y| \mu, \sigma)dy 

# 累積分布
# pnorm(1.8, 0, 1) - pnorm(1.2, 0, 1)
>>> sct.norm.cdf(1.8, 0, 1) - sct.norm.cdf(1.2, 0, 1)
0.079139351108782452

確率は面積であることから，，長方形であると近似する．
この場合，高さは$p(y=1.5|0, 1)$，幅を$\Delta y = 1.8-1.2 = 0.6$とすれば，

# 確率密度
# dnorm(1.5, 0, 1) * 0.6
>>> sct.norm.pdf(1.5, 0, 1) * 0.6
0.077710557399535043

と近似ができていることがわかる．

最尤推定

$確率=確率密度関数 \times \Delta y$に基づく．

$N$人の人間集団の身長データを${\bf Y} = \{ y_i \}$とする．
ある$y_i$が$y_i-0.5\Delta y \leq y_i \leq y_i + 0.5\Delta y$である確率は，確率密度関数$p(y_i|0, 1)$と区間幅$\Delta y$の席であると近似できるから，
正規分布を使った統計モデルの（対数）尤度関数は．

\begin{eqnarray}
L(\mu, \sigma) &=& \prod_i p(y_i|\mu, \sigma)\times \Delta y \\
&=& \prod_i \frac{1}{\sqrt{2\pi\sigma^2}}\exp \left\{ -\frac{(y-\mu)^2}{2\sigma^2}\right\}  \Delta y \\
log L(\mu, \sigma) &=& \sum_i \left\{-\log \sqrt{2\pi\sigma^2} + \log \Delta y - \frac{(y-\mu)^2}{2\sigma^2}    \right\} \\
&=& -0.5N\log(2\pi\sigma^2) + N\log \Delta y - \frac{1}{2\sigma^2}\sum_i (y-\mu)^2
\end{eqnarray}

となる．なお$\Delta y$は定数であり，パラメータ＄\{\mu, \sigma\}＄に影響しないため，
上式でも無視する．
したがって，

log L(\mu, \sigma) = -0.5N\log(2\pi\sigma^2)  - \frac{1}{2\sigma^2}\sum_i (y-\mu)^2

となる．

ガンマ分布のGLM

ガンマ分布は，確率変数の取りうる範囲が０以上の連続確率分布．
確率密度関数は．

p(y|s, r) = \frac{r^s}{\Gamma(s)}y^{s-1}\exp(-ry) 

$s$はshapeパラメータ，$r$はrateパラメータ，$\frac{1}{r}$はscaleパラメータとよび，$\Gamma(s)$はガンマ関数である．
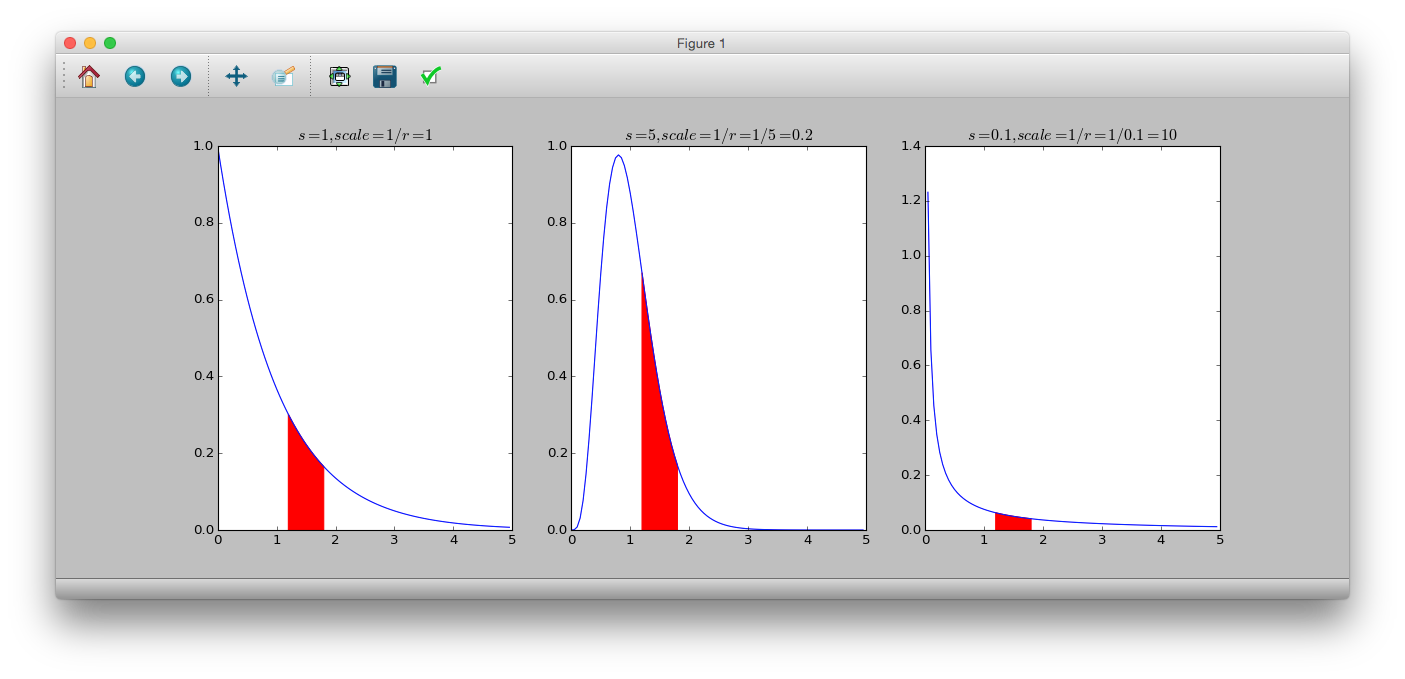
平均は$\frac{s}{r}$，分散は$\frac{s}{r^2}$となる．
また$s=1$のとき，指数分布となる．

# dgamma(y, shape, rate)
# 1/rate = scale
>>> y = numpy.arange(0, 5, 0.05)
>>> plt.subplot(131)
>>> plt.plot(y, sct.gamma.pdf(y, a=1, scale=1))
>>> plt.title('$s=1, scale=1/r=1$')
>>> plt.fill_between(numpy.arange(1.2, 1.8, 0.05), sct.gamma.pdf(numpy.arange(1.2, 1.8, 0.05), a=1, scale=1), color='r')
>>> plt.subplot(132)
>>> plt.plot(y, sct.gamma.pdf(y, a=5, scale=0.2))
>>> plt.title('$s=5, scale=1/r=1/5=0.2$')
>>> plt.fill_between(numpy.arange(1.2, 1.8, 0.05), sct.gamma.pdf(numpy.arange(1.2, 1.8, 0.05), a=5, scale=0.2), color='r')
>>> plt.subplot(133)
>>> plt.plot(y, sct.gamma.pdf(y, a=0.1, scale=10))
>>> plt.title('$s=0.1, scale=1/r=1/0.1=10$')
>>> plt.fill_between(numpy.arange(1.2, 1.8, 0.05), sct.gamma.pdf(numpy.arange(1.2, 1.8, 0.05), a=0.1, scale=10), color='r')
>>> plt.show()

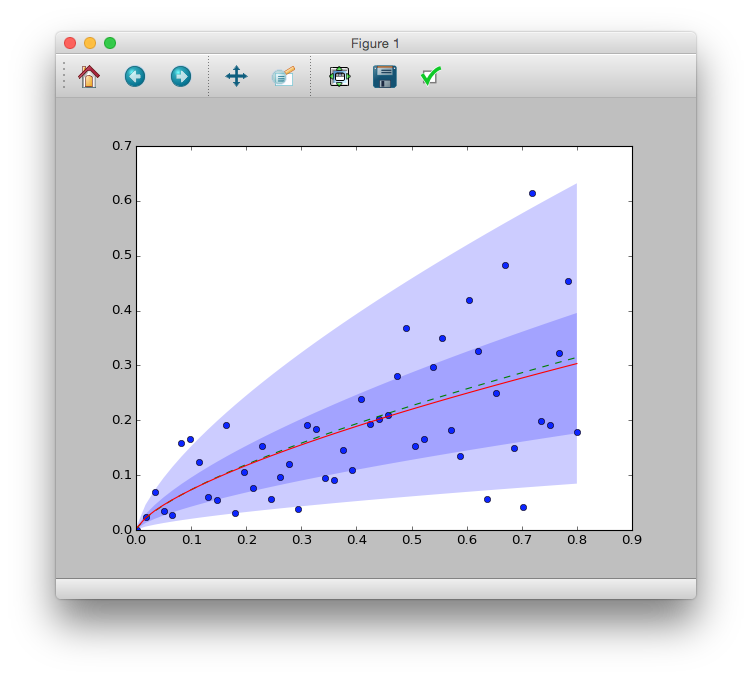
例題：架空植物の葉の重量と花の重量の関係

$x_i$が大きくなるにつれて，$y_i＄も大きくなっているようす．

\begin{eqnarray}
\mu_i &=& Ax_i^b \\
&=&\exp(a)x_i^b = \exp(a+b\log x_i) (\because A = \exp(a)) \\
\log\mu_i &=& a+blogx_i

\end{eqnarray}

>>> model = smf.glm('y ~ numpy.log(x)', data=d, family=sm.families.Gamma(link=sm.families.links.log))
>>> model.fit().summary()
                 Generalized Linear Model Regression Results
==============================================================================
Dep. Variable:                      y   No. Observations:                   50
Model:                            GLM   Df Residuals:                       48
Model Family:                   Gamma   Df Model:                            1
Link Function:                    log   Scale:                  0.325084605974
Method:                          IRLS   Log-Likelihood:                 58.471
Date:                Sat, 06 Jun 2015   Deviance:                       17.251
Time:                        20:38:39   Pearson chi2:                     15.6
No. Iterations:                    12
================================================================================
                   coef    std err          z      P>|z|      [95.0% Conf. Int.]
--------------------------------------------------------------------------------
Intercept       -1.0403      0.119     -8.759      0.000        -1.273    -0.808
numpy.log(x)     0.6832      0.068      9.992      0.000         0.549     0.817
================================================================================

get_y_mean = lambda b1, b2, x: numpy.exp(b1 + b2 * numpy.log(x))
model = smf.glm('y ~ numpy.log(x)', data=d, family=sm.families.Gamma(link=sm.families.links.log))
vc = model.fit().params

ax = plt.figure().add_subplot(111)
ax.plot(d.x, d.y, 'o')
ax.plot(d.x, get_y_mean(-1, 0.7, d.x),'--')
ax.plot(d.x, get_y_mean(vc[0], vc[1], d.x))


phi = model.fit().scale
m = get_y_mean(vc[0], vc[1], d.x)
scale = [(i * phi) for i in m]
shape = 1 / phi
def plot_pi(q):
    x = numpy.r_[numpy.array(d.x), numpy.array(d.x)[::-1]]
    y = numpy.r_[sct.gamma.ppf(q, a=shape, scale=scale), sct.gamma.ppf(1-q, a=shape, scale=scale)[::-1]]
    pair = [(x[i], y[i]) for i in range(len(x))]
    poly = plt.Polygon(pair, alpha=0.2, edgecolor='none')
    return poly
ax.add_patch(plot_pi(0.05))
ax.add_patch(plot_pi(0.25))

plt.show()