統計学 Advent Calendar 2025

多重検定問題とベイズ統計

Last updated at 2025-12-20Posted at 2025-12-20

はじめに

データ分析において複数の統計的仮説検定を実施することは珍しくありません。

しかし、検定を繰り返すことで生じる「多重検定問題」は、誤った結論を導く重大なリスクとなります。本記事では、多重検定問題の本質と、その対処法としてのベイズ統計の可能性について解説します。

統計的仮説検定の限界と本記事の立場

本記事で扱う多重検定問題とその対処法を理解する前に、統計的仮説検定そのものの限界を認識しておくことが重要です。

P値が意味するもの

P値は「帰無仮説が真である場合に、観測されたデータ（またはそれ以上に極端なデータ）が得られる確率」です。これは以下を意味しません：

❌ 帰無仮説が真である確率
❌ 対立仮説が真である確率
❌ 効果が実在する確率

⚠️ 重要: たとえP < 0.05であっても、それだけでは帰無仮説を「否定した」「証明した」とは言えません。P値は証拠の強さを示す指標の一つに過ぎず、効果量、信頼区間、研究の文脈などを総合的に判断する必要があります。

本記事の立場

本記事では、多重検定による「偽陽性率の増加」という技術的問題とその対処法を扱います。ただし、これらの手法を用いても：

統計的有意性 ≠ 科学的重要性
補正後のP値 < α でも、帰無仮説が偽とは限らない
すべての統計的推論には不確実性が伴う（頻度論もベイズ統計も）

これらの限界を理解した上で、適切な統計的推論を行うことを目指します。

多重検定問題とは

問題の定義

多重検定問題（multiple testing problem）とは、複数の統計的仮説検定を実施することで、偶然による偽陽性（第一種過誤）の確率が累積的に増加する現象です¹。

数学的な説明

有意水準 $ \alpha = 0.05$ で独立なm回の検定を行った場合、少なくとも1回は誤って帰無仮説を棄却する確率（Family-wise Error Rate: FWER）は以下のように計算されます：

\begin{align}
{\rm FWER} &= 1 - (1 - \alpha)^m
\end{align}

Number of tests: 1, FWER at alpha=0.05: 0.0500
Number of tests: 5, FWER at alpha=0.05: 0.2262
Number of tests: 10, FWER at alpha=0.05: 0.4013
Number of tests: 20, FWER at alpha=0.05: 0.6415
Number of tests: 50, FWER at alpha=0.05: 0.9231
Number of tests: 100, FWER at alpha=0.05: 0.9941

これは、20回検定を行えば、真の効果がなくても約64%の確率で少なくとも1つの「有意な」結果が得られることを意味します。

ここで、全く同じ内容を繰り返すわけではないことに注意してください。
例えば、薬Aと薬Bについて、複数の観点で効果を検証する場合、各観点ごとに独立した検定が行われるため、多重検定問題が発生します。

頻度論的アプローチにおける対処法

1. ボンフェローニ補正

最も単純な方法で、有意水準をα/mに調整します²。

{\rm P-value\ threshold} = \frac{\alpha}{m}

P-value: 0.001, Bonferroni threshold for m=10 at alpha=0.05: 0.0050, Significant: True
P-value: 0.01, Bonferroni threshold for m=10 at alpha=0.05: 0.0050, Significant: False
P-value: 0.02, Bonferroni threshold for m=10 at alpha=0.05: 0.0050, Significant: False
P-value: 0.03, Bonferroni threshold for m=10 at alpha=0.05: 0.0050, Significant: False
P-value: 0.04, Bonferroni threshold for m=10 at alpha=0.05: 0.0050, Significant: False
P-value: 0.05, Bonferroni threshold for m=10 at alpha=0.05: 0.0050, Significant: False
P-value: 0.06, Bonferroni threshold for m=10 at alpha=0.05: 0.0050, Significant: False
P-value: 0.07, Bonferroni threshold for m=10 at alpha=0.05: 0.0050, Significant: False
P-value: 0.08, Bonferroni threshold for m=10 at alpha=0.05: 0.0050, Significant: False
P-value: 0.09, Bonferroni threshold for m=10 at alpha=0.05: 0.0050, Significant: False

上記の例では、p値が0.001のみが有意と判定されます。

利点：実装が簡単、FWERを確実に制御
欠点：保守的すぎて検出力が低下（第二種過誤の増加）

2. Holm法

段階的に有意水準を調整する方法で、ボンフェローニ法より検出力が高い³。

def calc_holm_bonferoni_method(p_values: list, alpha: float):
    sorted_p_values = sorted(p_values)
    m = len(p_values)
    significant = []
    for i, p in enumerate(sorted_p_values):
        threshold = alpha / (m - i)
        if p < threshold:
            significant.append(p)
        else:
            break
    return significant

p_values = [0.001, 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09]
significant_holm = calc_holm_bonferoni_method(p_values, 0.05)
print(f"Significant p-values using Holm-Bonferroni method at alpha=0.05: {significant_holm}")
# Significant p-values using Holm-Bonferroni method at alpha=0.05: [0.001]

利点：FWERを制御しつつ、ボンフェローニ法より検出力が高い
欠点：依然として保守的であり、多数の検定では検出力が低下する可能性

3.Benjamini-Hochberg法

偽発見率（False Discovery Rate: FDR）を制御する方法もあります⁴。
今までは、一度でも誤って帰無仮説を棄却する確率（FWER）を制御してきましたが、FDRは「棄却された帰無仮説のうち、誤って棄却された割合」を制御します。

この手法は特に検出力を重視するため、発見を増やしたい探索的データ分析に適しています。

def benjamini_hochberg_method(p_values: list, alpha: float):
    sorted_p_values = sorted(p_values)
    m = len(p_values)
    significant = []
    for i, p in enumerate(sorted_p_values):
        threshold = (i + 1) / m * alpha
        if p < threshold:
            significant.append(p)
    return significant


significant_bh = benjamini_hochberg_method(p_values, 0.05)
print(f"Significant p-values using Benjamini-Hochberg method at alpha=0.05: {significant_bh}")
# Significant p-values using Benjamini-Hochberg method at alpha=0.05: [0.001, 0.01]

ベイズ統計における多重検定へのアプローチ

ベイズ統計では、頻度論的な「多重検定補正」という考え方が本質的に不要となる場合が多いです。なぜなら、ベイズ推論は各パラメータの事後分布を直接計算し、検定の回数や有意水準の調整に依存せず、データと事前分布から一貫した推論を行うからです。

なぜベイズ推論では多重検定問題が発生しにくいのか

頻度論では、複数の検定を繰り返すことで「偶然の有意差」が増え、第一種過誤（偽陽性）が累積します。これに対し、ベイズ推論では「パラメータごとに事後分布 $p(\theta_j|D)$ を計算」するため、検定の回数が増えても、各パラメータの推定が独立している限り、誤検出率がインフレしません。

さらに、ベイズ階層モデルを用いることで、複数パラメータ間の情報共有（shrinkage）が自動的に行われ、極端な推定値が抑制されます。これが「多重比較補正」と同等、あるいはそれ以上の効果をもたらします。

階層ベイズモデルの数式例

例えば、$J$群の平均比較問題を考えます。

観測データ $y_{ij}$（$i$番目のサンプル, $j$群）に対し、

\begin{align}
    y_{ij} &\sim \mathcal{N}(\mu_j, \sigma^2) \\
    \mu_j &\sim \mathcal{N}(\mu_0, \tau^2) \\
    \mu_0 &\sim \mathcal{N}(m_0, s_0^2) \\
    \sigma &\sim \mathrm{HalfNormal}(s_1) \\
    \tau &\sim \mathrm{HalfNormal}(s_2)
\end{align}

ここで、

$\mu_j$ : 各群の平均（パラメータ）
$\mu_0$ : 全体平均（ハイパーパラメータ）
$\tau$ : 群間分散（全体平均からのばらつき）
$\sigma$ : 観測ノイズ
$m_0, s_0, s_1, s_2$ : 事前分布のパラメータ（適宜設定）

このモデルでは、各群の平均 $\mu_j$ は全体平均 $\mu_0$ のまわりに正規分布し、$\tau$ が小さいほどが制約が強くなります。

事前分布の形

$\mu_0$ には広い正規分布（例: $\mathcal{N}(0, 10^2)$）
$\tau, \sigma$ には半正規分布（例: $\mathrm{HalfNormal}(1)$）
など、ドメイン知識や目的に応じて設定します。

事後分布の数式

事後分布は次のように表されます：

\begin{align}
    p(\{\mu_j\} | D) &= \int p(\{\mu_j\}, \mu_0, \sigma, \tau | D) d\mu_0 d\sigma d\tau \\
    &= \frac{1}{p(D)} \int p(D | \{\mu_j\}, \sigma) p(\{\mu_j\} | \mu_0, \tau) p(\mu_0) p(\sigma) p(\tau) d\mu_0 d\sigma d\tau \\
    &\propto \int p(D | \{\mu_j\}, \sigma) p(\{\mu_j\} | \mu_0, \tau) p(\mu_0) p(\sigma) p(\tau) d\mu_0 d\sigma d\tau
\end{align}

上記の内容は直接的に計算を行うのが難しいため、MCMC法などの数値的手法で近似して求めます。

階層モデルによる自動的な調整

ベイズ統計における多重比較の最も強力な対処法は、階層モデル（hierarchical model）の使用です⁵⁶。

頻度論との比較例：複数群の平均比較

頻度論的アプローチ:

from scipy import stats

# 3群のデータ
group1 = [5.2, 5.8, 6.1, 5.5, 5.9]
group2 = [5.5, 6.2, 6.4, 5.8, 6.0]
group3 = [7.1, 7.5, 7.8, 7.3, 7.6]

# 対ごとにt検定を実施
p_values = []
p_values.append(stats.ttest_ind(group1, group2)[1])  # p=0.2433
p_values.append(stats.ttest_ind(group1, group3)[1])  # p=0.0000
p_values.append(stats.ttest_ind(group2, group3)[1])  # p=0.0001

# ボンフェローニ補正
alpha = 0.05
bonferroni_threshold = alpha / len(p_values)
print(f"補正後の閾値: {bonferroni_threshold:.4f}")

for i, p in enumerate(p_values):
    print(f"Group {i+1} p-value: {p:.4f} -> {'有意' if p < bonferroni_threshold else '有意でない'}")

補正後の閾値: 0.0167
Group 1 p-value: 0.2433 -> 有意でない
Group 2 p-value: 0.0000 -> 有意
Group 3 p-value: 0.0001 -> 有意

ベイズ階層モデルアプローチ:

import pymc as pm
import arviz as az
import numpy as np

y = np.concatenate([group1, group2, group3])
group_idx = np.repeat([0, 1, 2], 5)

with pm.Model() as hierarchical_model:
    # ハイパー事前分布（全群に共通）
    mu_global = pm.Normal("mu_global", mu=6, sigma=2)
    sigma_global = pm.HalfNormal("sigma_global", sigma=1)

    # 各群の平均は全体平均から「借用」される（shrinkage）
    mu = pm.Normal("mu", mu=mu_global, sigma=sigma_global, shape=3)

    # 観測モデル
    sigma = pm.HalfNormal("sigma", sigma=1)
    y_obs = pm.Normal("y_obs", mu=mu[group_idx], sigma=sigma, observed=y)

    # 群間差の計算
    diff_1_2 = pm.Deterministic("diff_1_2", mu[0] - mu[1])
    diff_1_3 = pm.Deterministic("diff_1_3", mu[0] - mu[2])
    diff_2_3 = pm.Deterministic("diff_2_3", mu[1] - mu[2])

    trace = pm.sample(2000, tune=1000, return_inferencedata=True,
                      random_seed=RANDOM_SEED,
                      target_accept=0.95,
                      idata_kwargs={"log_likelihood": True})

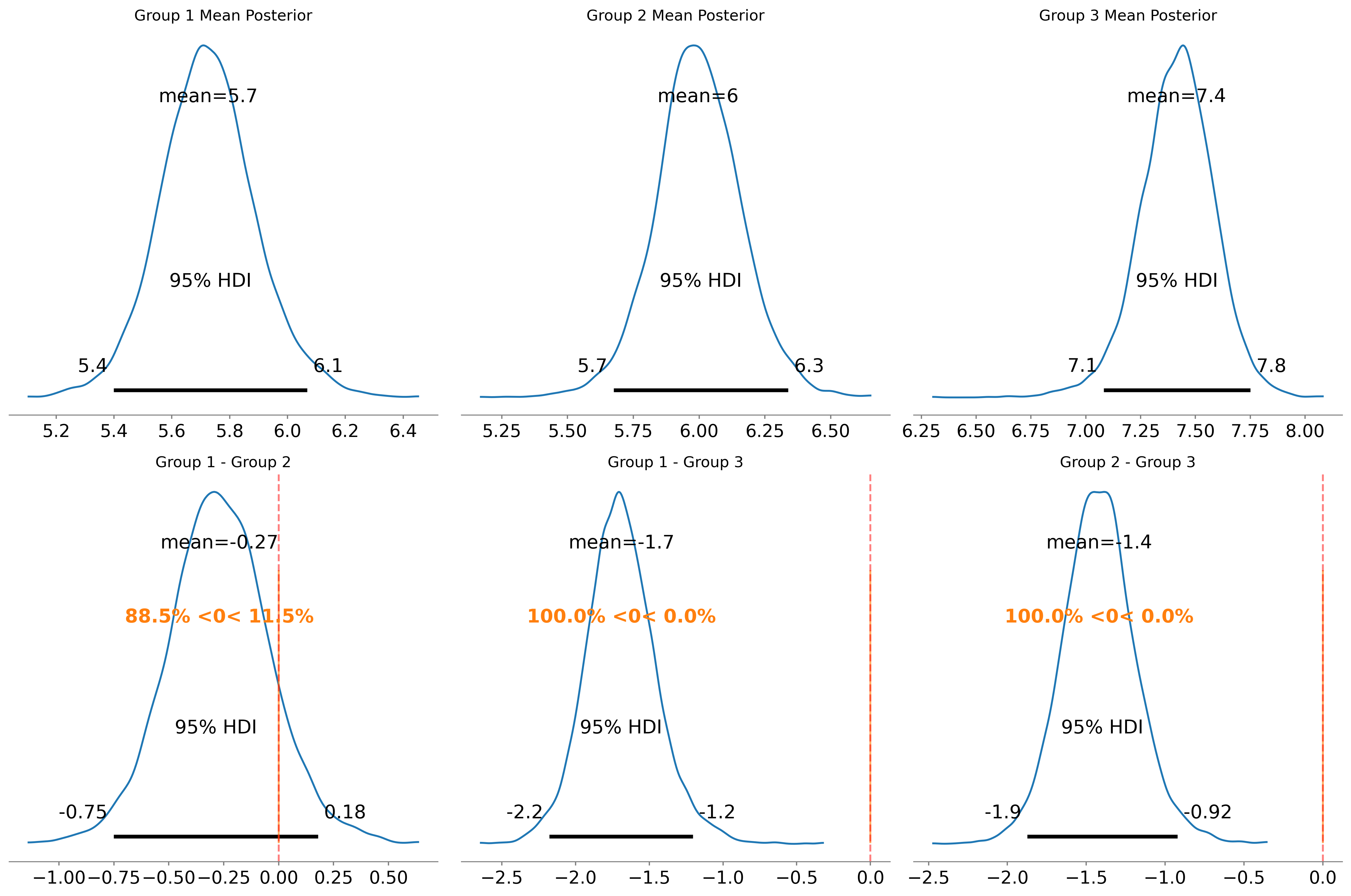
# 事後分布の要約
summary = az.summary(
    trace, var_names=["diff_1_2", "diff_1_3", "diff_2_3"],
    hdi_prob=0.95,
)
print(summary)

           mean     sd  hdi_2.5%  hdi_97.5%  mcse_mean  mcse_sd  ess_bulk  ess_tail  r_hat
diff_1_2 -0.269  0.233    -0.751      0.179      0.003    0.003    7962.0    5138.0    1.0
diff_1_3 -1.688  0.242    -2.179     -1.204      0.004    0.004    5279.0    3958.0    1.0
diff_2_3 -1.419  0.237    -1.874     -0.922      0.003    0.004    6829.0    4402.0    1.0

階層モデルの利点

階層モデルでは、各群の推定値が全体平均に向かって引き寄せられるため、自動的に極端な推定が抑制されます。これは以下の点で頻度論的補正と異なります：

観点	頻度論的補正	ベイズ階層モデル
調整の仕組み	有意水準を厳しくする	パラメータ推定値自体を調整
情報の利用	各検定は独立	全群のデータを相互に活用
検出力	保守的で低下しやすい	情報共有により維持されやすい

合わせて、95%信用区間を計算することで、多重比較の影響を考慮した推定が可能です：

# 95%同時信用区間の計算
# 各パラメータで95%信用区間を持つ確率が、全体として(1-α)になるように調整
hdi_95 = az.hdi(
    trace, var_names=["diff_1_2", "diff_1_3", "diff_2_3"],
    hdi_prob=0.95,
)
print(hdi_95)

Data variables:
    diff_1_2  (hdi) float64 16B -0.7514 0.1787
    diff_1_3  (hdi) float64 16B -2.179 -1.204
    diff_2_3  (hdi) float64 16B -1.874 -0.9221

モデルの比較の活用

複数の仮説がある場合、情報量規準を用いてモデル全体を比較することができます：

# モデル1: 全群が同じ平均
with pm.Model() as model_null:
    mu = pm.Normal("mu", mu=6, sigma=2)
    sigma = pm.HalfNormal("sigma", sigma=1)
    y_obs = pm.Normal("y_obs", mu=mu, sigma=sigma, observed=y)
    trace_null = pm.sample(2000, return_inferencedata=True,
                           random_seed=RANDOM_SEED,
                           idata_kwargs={"log_likelihood": True})

# モデル2: 各群が異なる平均（上記のhierarchical_model）
comparison = az.compare(
    {
        "null": trace_null,
        "hierarchical": trace,
    },
    ic="waic",
)
print("モデル比較結果:")
print(comparison)

              rank  elpd_waic    p_waic  elpd_diff  weight        se       dse  warning scale
hierarchical     0  -7.068889  2.921276   0.000000     1.0  1.752367  0.000000     True   log
null             1 -20.108834  1.290141  13.039946     0.0  1.736012  2.182345    False   log

頻度論的多重検定との違い：

頻度論: 各検定で帰無仮説を「棄却/非棄却」と個別に判断
ベイズ: 複数のモデル全体を同時に比較し、相対的な証拠の強さを定量化

ベイズアプローチの注意点とリスク

1. データ駆動的なモデル構築の危険性

ベイズ統計でも、データを見てから事前分布やモデル構造を決める行為は問題です⁷。

悪い例:

データを見てから、都合の良い事前分布を選ぶ
これは頻度論の p-hacking と同様の問題
最初: 弱情報事前分布で分析 → 期待した結果が出ない
次: 強情報事前分布に変更 → 都合の良い結果を報告

対策:

事前分布の選択肢を事前に定義
複数の事前分布で感度分析を実施し、結果を報告

2. "Garden of Forking Paths" 問題

Gelman & Loken (2013)⁷が指摘するように、研究者の自由度（researcher degrees of freedom）はベイズ統計でも存在します：

外れ値の扱いを変える
異なる変数変換を試す
複数のモデルを試して良い結果だけ報告

対策

多重検定問題への対策を3段階に分けて提案します。

研究設計段階

事前に仮説を絞る：理論的根拠のある仮説に限定することで、多重性を減らせます。
事前登録：解析計画を事前に公開し、HARKing（Hypothesizing After Results are Known）を避けます⁸。

解析段階

探索的分析と検証的分析を明確に区別：探索的分析ではFDR制御、検証的分析では厳格なFWER制御を検討します。
効果量と信頼区間を報告：p値だけでなく、効果の大きさと不確実性を示します。

報告段階

実施したすべての検定を報告：有意な結果だけでなく、非有意な結果も含めます。
補正方法の明示：どの多重検定補正を用いたか、または用いなかった理由を説明します。
生データと解析コードの公開：再現性を担保します。

まとめ

多重検定問題は統計的推論における重要な課題であり、適切な対処が必要です。頻度論的アプローチでは補正法が確立されていますが、ベイズ統計は以下の点で魅力的な代替手段です：

事前情報を体系的に組み込める
複数の仮説を柔軟に比較できる

ただし、ベイズ統計も万能ではなく、透明性と誠実さが依然として重要です。最終的には、研究の文脈や目的に応じて適切な手法を選択し、分析の限界を認識することが大切です。

今回使用したコードは以下のURLで公開しています：

参考文献

Multiple comparisons problem - Wikipedia ↩
ボンフェローニ補正 - Wikipedia ↩
ホルム＝ボンフェローニ法 - Wikipedia ↩
False discovery rate - Wikipedia ↩
[0907.2478v1] Why we (usually) don't have to worry about multiple comparisons ↩
階層ベイズモデル - Wikipedia ↩
Gelman, Andrew, and Eric Loken. "The garden of forking paths: Why multiple comparisons can be a problem, even when there is no “fishing expedition” or “p-hacking” and the research hypothesis was posited ahead of time." Department of Statistics, Columbia University 348.1-17 (2013): 3. ↩ ↩²
Nosek, Brian A., et al. "The preregistration revolution." Proceedings of the National Academy of Sciences 115.11 (2018): 2600-2606. ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up