More than 1 year has passed since last update.

　書籍「Pytorch&深層学習プログラミング」２章補足　sum関数で微分計算ができる理由

Last updated at 2022-05-01Posted at 2022-04-30

はじめに

書籍「Pytorch&深層学習プログラミング」の著者です。

この書籍の２章p.81-p.87にかけてPyTorchの勾配計算機能を使い、関数の導関数を計算し、グラフ表示をしてます。
そこでは、

import numpy as np
import torch

# xをnumpy配列で定義
x_np = np.arange(-2, 2.1, 0.25)

# 勾配計算用変数の定義
x = torch.tensor(x_np, requires_grad=True, 
    dtype=torch.float32)

# 2次関数の計算　裏で計算グラフが自動生成される
y = 2 * x**2 + 2

# 勾配計算のためには、最終値はスカラーの必要があるため、sum関数をかける
z = y.sum()

# 勾配計算
z.backward()

# 勾配値の取得
print(x.grad)

というコードにより、関数 $f(x)=2x^2+2$ の微分計算をしています。

読者から「なぜここでz = y.sum()と和を取ることでこの微分計算ができるのかわからない」という質問を受けました。
この質問が出るのはもっともで、書籍の中では、「なぜsum関数なのか。スカラーにしたいなら、mean関数やmax関数ではダメなのか。」という疑問に答える説明が一切されていませんでした。
一方で、このことを正確に説明しようとすると、どうしても偏微分など数学の知識が必要になります。当記事は、この疑問点を数式を使ってできるだけ正確に説明する目的で作成しました。
「sum関数の代わりにmean関数やmax関数を使うとどうなるか」という実験もやってみたので、その結果もあわせて共有することにします。

数学的な解説

z = y.sum() を数学的に書き直すと、

$z = \displaystyle \sum_{i=0}^{16} y_i$

ということになります。

ここで$z$を$y_k$で偏微分します。すると以下の結果になります。

$\dfrac{\partial z}{\partial y_k}=\dfrac{\partial}{\partial y_k}\displaystyle \sum_{i=0}^{16} y_i=1$

そこで、$z$を$x_k$で偏微分すると合成関数の微分公式(推移律)から、次の式が成り立ちます。

$\dfrac{\partial z}{\partial x_k}=\dfrac{\partial z}{\partial y_k}\cdot\dfrac{dy_k}{dx_k}=1\cdot f'(x_k)=f'(x_k)$

sum関数をmean関数に置き換える、つまりz = y.mean()とした場合、数学的に$z$は次の式で表されます。

$z = \dfrac{1}{17}\displaystyle \sum_{i=0}^{16} y_i$

なので、この場合も勾配計算により関数の微分をすることはできますが、結果はsum関数を使った場合の$\frac{1}{17}$になります。

実装コードで確認

以下の実装コードは、次のリンク　実装コードに全量をアップしています。

事前準備コード

事前準備で必要なコードを一つにまとめると以下のとおりです。

!pip install torchviz | tail -n 1
import numpy as np
import matplotlib.pyplot as plt
import torch
from torchviz import make_dot

plt.rcParams['font.size'] = 14
plt.rcParams['figure.figsize'] = (6,6)
plt.rcParams['axes.grid'] = True

x_np = np.arange(-2, 2.1, 0.25)

sum関数の場合

書籍オリジナルのコードを、1つのセルにまとめると以下になります。

# 勾配計算用変数の定義
x = torch.tensor(x_np, requires_grad=True, 
    dtype=torch.float32)

# 2次関数の計算
# 裏で計算グラフが自動生成される
y = 2 * x**2 + 2

# 勾配計算のためには、最終値はスカラーの必要があるためsum関数をかける
z = y.sum()

# 可視化関数の呼び出し
g= make_dot(z, params={'x': x})
display(g)

# 勾配計算
z.backward()

# 勾配値の取得
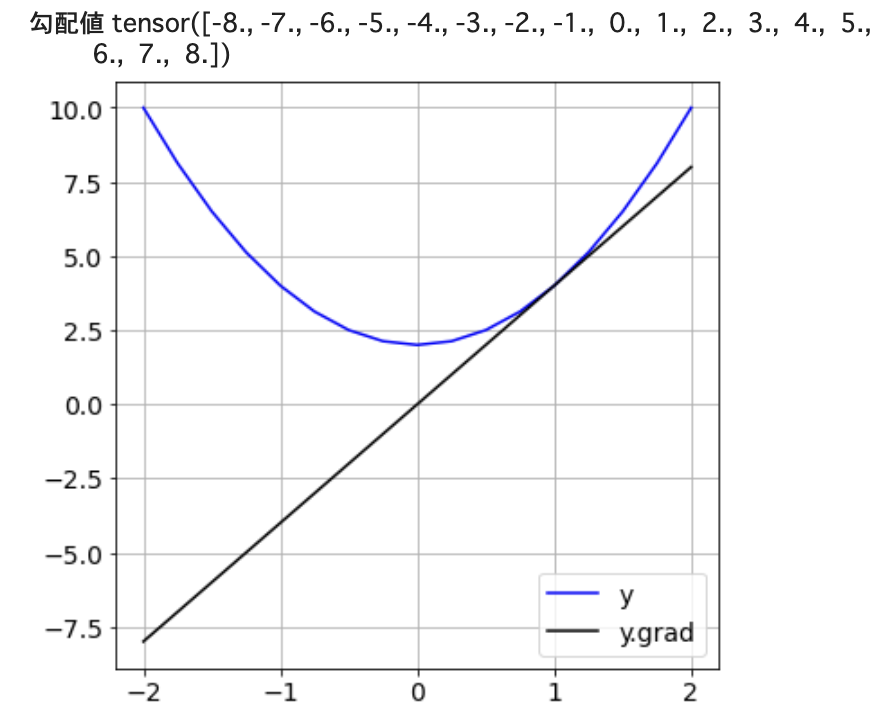
print('勾配値', x.grad)

# 元の関数と勾配のグラフ化
plt.figure(figsize=(6,6))
plt.plot(x.data, y.data, c='b', label='y')
plt.plot(x.data, x.grad.data, c='k', label='y.grad')
plt.legend()
plt.show()

結果は以下になります・

計算グラフ

勾配計算結果

sum関数を使わず、ループを回して各要素を加算した場合

sum関数を使わず、ループを回して各要素を加算した場合は以下のとおりです。
数学的に同じ計算なので、勾配計算の結果はsum関数と同じですが、計算グラフは別のものになります。

# 勾配計算用変数の定義
x = torch.tensor(x_np, requires_grad=True, 
    dtype=torch.float32)

# 2次関数の計算
# 裏で計算グラフが自動生成される
y = 2 * x**2 + 2

# 勾配計算のためには、最終値はスカラーの必要があるためsum関数をかける
z = torch.tensor(0.0)
for y1 in y:
    z += y1

# 可視化関数の呼び出し
g= make_dot(z, params={'x': x})
display(g)

# 勾配計算
z.backward()

# 勾配値の取得
print('勾配値', x.grad)

# 元の関数と勾配のグラフ化
plt.figure(figsize=(6,6))
plt.plot(x.data, y.data, c='b', label='y')
plt.plot(x.data, x.grad.data, c='k', label='y.grad')
plt.legend()
plt.show()

計算グラフ

勾配計算結果

mean関数の場合

sum関数の代わりにmean関数を使った場合のコードと、その結果を以下に示します。

# 勾配計算用変数の定義
x = torch.tensor(x_np, requires_grad=True, 
    dtype=torch.float32)

# 2次関数の計算
# 裏で計算グラフが自動生成される
y = 2 * x**2 + 2

# 勾配計算のためには、最終値はスカラーの必要があるため、関数をかける
z = y.mean()

# 可視化関数の呼び出し
g= make_dot(z, params={'x': x})
display(g)

# 勾配計算
z.backward()

# 勾配値の取得
print('勾配値', x.grad)

# 元の関数と勾配のグラフ化
plt.figure(figsize=(6,6))
plt.plot(x.data, y.data, c='b', label='y')
plt.plot(x.data, x.grad.data, c='k', label='y.grad')
plt.legend()
plt.show()