はじめに
この記事は、別記事書籍「Pytorch&深層学習プログラミング」2章補足 sum関数で微分計算ができる理由の続編です。
前の記事では、$y=f(x)$の値の1階テンソルをsum関数で集約すると微分計算ができること、mean関数だと、微分計算ができるが、値は導関数値をデータ個数で割ったものになることを示しました。
この記事のテーマは、代わりにmax関数を使うとなにがおきるかということです。
実装と結果
事前準備コード
事前準備で必要なコードを一つにまとめると以下のとおりです。
!pip install torchviz | tail -n 1
import numpy as np
import matplotlib.pyplot as plt
import torch
from torchviz import make_dot
plt.rcParams['font.size'] = 14
plt.rcParams['figure.figsize'] = (6,6)
plt.rcParams['axes.grid'] = True
x_np = np.arange(-2, 2.1, 0.25)
max関数を利用した場合
# 勾配計算用変数の定義
x = torch.tensor(x_np, requires_grad=True,
dtype=torch.float32)
# 2次関数の計算
# 裏で計算グラフが自動生成される
y = 2 * x**2 + 2
# スカラー化のためにmax関数を利用する
z = y.max()
# 可視化関数の呼び出し
g= make_dot(z, params={'x': x})
display(g)
# 勾配計算
z.backward()
# 勾配値の取得
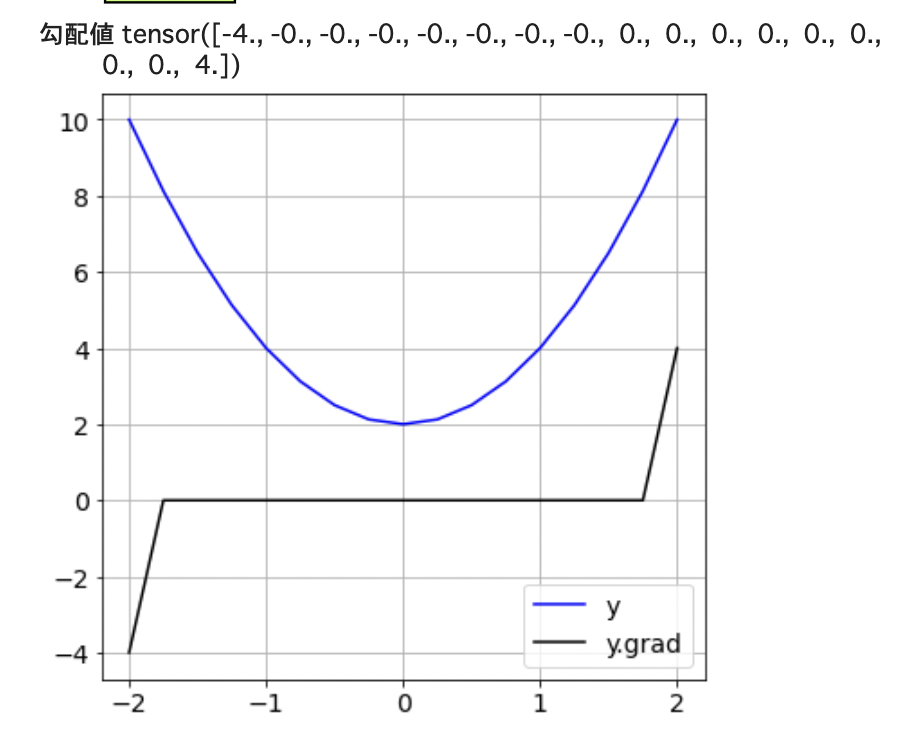
print('勾配値', x.grad)
# 元の関数と勾配のグラフ化
plt.figure(figsize=(6,6))
plt.plot(x.data, y.data, c='b', label='y')
plt.plot(x.data, x.grad.data, c='k', label='y.grad')
plt.legend()
plt.show()
結果は以下になります・
数学的な解説
上の勾配計算の結果は、次の2つであると読み取れます。
(1) 両端の点を除いた15個の点では勾配値はゼロ
(2) $x=-2.0$と$x=2.0$の両端では、勾配値は、それぞれの導関数値の1/2
(2)は、第1部のsum関数の結果と比較することでわかります。
今回の問題では、まずxとして、-2から2までの等間隔の17個の点を取りました。
具体的には
$x_0 = -2.0$
$x_1 = -1.75$
:
:
$x_{15} = 1.75$
$x_{16} = 2.0$
次に$y = f(x) = 2x^2+2$により、それぞれの点に対応するyの値を求めています。
$y_0 = f(x_0)$
$y_1 = f(x_1)$
:
:
$y_{15} = f(x_{15})$
$y_{16} = f(x_{16})$
そして、zは$y_0, y_1, ..., y_{15}, y_{16}$の最大値として定義しています。
最大値は、実際にはxの端点($x_0とx_{16}$)で決まっている点に注意して下さい。
この前提で、(1)について考えてみます。
勾配値とは、
注目している変数(今は$x_k$)を微少量変化させたとき、目的とする変数(今は$z$)がどの程度変化するかを元に計算される
という点が重要でです。
$x_1$のような端点でない点を微少量変化させたとしても、最大値zは変化しません。
このことはつまり端点以外の$x_k$では勾配値はゼロであることを意味します。
では、(2)についてはどうでしょうか?
端点の一つである$x_{16}=2.0$に注目し、この値を微少量増やしたとき、zがどう変化するか考えてみます。
現在は、$x_0とx_{16}$で同時に最大値10.0を取っていますが、 値を微少量増やすと、$x_{16}$だけで最大値を取るようになります。その増え方は、値の増分をhとすると、およそ$f'(x)\cdot h$になります。
今度は値を微少量減らすことを考えます。すると、面白いことが起きます。$f(x_{16})$の値は微少量減るのですが、最大値zということで考えると、$f(x_0)$の値は変化しないので、変化なしになります。
ここで、書籍でも示している以下の数値微分を考えてみます。
hを微少量としたとき、
$f'(x)=\dfrac{f(x+h)-f(x-h)}{2h}$
で計算しています。
$f(x+h)-f(x-h) = (f(x+h)-f(x)) + (f(x)-f(x-h))$
と分解して考えてみると、前半の
$f(x+h)-f(x)$の部分は普通通りの微少量の変化があり、その大きさはおよそ$f'(x)\cdot h$であるのに対して、後半の$f(x)-f(x-h))$の部分は、変化量がゼロということになります。
そのため、全体としての勾配値は通常の導関数値の1/2になるのです。
左側の端点である$x_0$に関しても、zの値が変化しない領域が逆になるだけで、あとは同じ考え方で、勾配値が通常の1/2になることが説明できます。
以上で、今回の事象の説明は100%できたことになります。
あわせて、著者として確認できたことがあります。数値微分の公式が上で示したものであることは、知識としては持っていたのですが、実はPyTorchで本当にこの実装をしているかは、ソースレベルで裏取りはしていなかったです。
今回の検証により、間接的ではありますが、PyTorchの勾配計算の実装で上の公式を使っていることがわかったことになり、著者としても一安心した次第です。