潜在変数モデルの詳細な解説

はじめに

書籍『Pythonでスラスラわかる ベイズ推論「超」入門』著者です。
本書は「超」入門といっておきながら、一部、やや複雑な確率モデルの話にも踏み込んでいます。その中でも最も難しい話が5.4節の「潜在変数モデル」です。
そのため、出版後に読者からいただく質問も、この節を対象にしたものに集中しています。
今回、GithubのIssueでいただいた質問は、かなり本質をついたものだと思っており、この質問に当記事を通じて丁寧に回答していきたいと考えています。
今回、ご質問いただいた読者の方にはこの場を借りて厚く御礼いたします。
なお、以下の記事は、本書の読者向けのものであり、書籍の中で説明済みの前提概念はすべて省略しています。不明点がある場合は、本書をお読みいただければと思いますので、そのようにご理解ください。

質問内容

次の2つの質問をいただいています。

---

Q1. 各サンプルがversicolorに属するのかvirginicaに属するのかをベルヌーイ分布からサンプリングされた値から判断できることを示唆していました。ここでベルヌーイ分布の母数pをサンプルの数だけ個別に用意していないのにも関わらず、サンプルごとに0か1か大まかに分類できていたのはなぜでしょうか。pがエポック毎に一様分布から1つサンプリングされるのであれば0、1のラベルはサンプルに関係なくランダムに付与されるのではないかと思いました。

 Q2. 本節ではsigmaの代わりにtauを使って分布の広がり具合を表していましたがsigmaを使うと失敗する原因は何でしょうか?

---

説明用実習コード

この2つの疑問点を解説するため、次のような実習コードを準備しました。

5_4_潜在変数モデル_簡略版.ipynb

(Q1)への回答

書籍の実習コードとの本質的な違いは、以下の確率モデル定義の部分です。

# 変数の初期設定

# 何種類の正規分布モデルがあるか
n_components = 2

# 観測データ件数
N = X.shape

model1 = pm.Model()

with model1:
    # Xの観測値をConstantDataとして定義
    X_data = pm.ConstantData('X_data', X)

    # pを確率変数でなく定数にした
    p = 0.5

    # s: 潜在変数pの確率値をもとに0, 1のいずれかの値を返す
    s = pm.Bernoulli('s', p=p, shape=N)

    # mus: ２つの花の種類毎の平均値
    mus = pm.Normal('mus', mu=0.0, sigma=10.0, shape=n_components)

    # taus: 2つの花の種類毎のバラツキ
    # 標準偏差sigmasとの間にはtaus = 1/(sigmas*sigmas)の関係がある
    taus = pm.HalfNormal('taus', sigma=10.0, shape=n_components)

    # グラフ描画など分析でsigmasが必要なため、tausからsigmasを求めておく
    sigmas = pm.Deterministic('sigmas', 1/pm.math.sqrt(taus))

    # 各観測値ごとに潜在変数からmuとtauを求める
    mu = pm.Deterministic('mu', mus[s])
    tau = pm.Deterministic('tau', taus[s])

    # 正規分布に従う確率変数X_obsの定義
    X_obs = pm.Normal('X_obs', mu=mu, tau=tau, observed=X_data)

実習コードと比較していただければわかるとおり、書籍コードで

    # p: 潜在変数が1の値をとる確率
    p = pm.Uniform('p', lower=0.0, upper=1.0)

となっている部分が

    # pを確率変数でなく定数にした
    p = 0.5

に変わっています。確率変数であったpを固定値0.5にしています。
これは、「2つのクラスの件数比が0.5ずつである」ということが事前情報としてわかっている」ことに対応していて、オリジナルの問題と比較して場合、よりやさしい問題になっています。
しかし、このように問題設定を変更をしても「潜在変数モデル」としては成り立ちます。
そのことを説明していきます。

まず、この場合、いつも書籍で作っていた確率モデル可視化結果がどうなるかです。
以下のような形になります。

p=0.5のベルヌーイ分布に従う確率変数がs[0]からs[99]まで計100個作られます。
注意いただきたいのは、これら100個の確率変数は、事前分布は「p=0.5のベルヌーイ分布」という共通のものですが、観測値が異なるので事後分布はそれぞれ別々のものになるということです。
これが、いただいたご質問(Q1)に対する本質的な回答ということになります。

書籍の確率モデルと、ここで説明に使った確率モデルの違いは、今までの説明でご理解いただけたかと思います。
潜在変数モデルという意味においては、この簡易版でも実現している訳ですが、書籍の確率モデルは、より難易度を上げて、「2つのクラスタの比率も確率変数化し、この比率も個別の潜在変数の確率分布と同時に当てにいく」ということをやっています。
私自身も、この確率モデルの仕組みを理解したとき、ベイズモデルの凄さを実感した部分となります。

(Q2)への回答

いただいたご質問は非常に難しいものであり、私自身も100%説明ができる形にはなっていないという認識です。
ただし、この疑問を解決するヒントになるコードを説明用実習Notebookに含めました。
具体的には、以下の確率モデルを作ることをしてみます。

model2 = pm.Model()

with model2:
    # Xの観測値をConstantDataとして定義
    X_data = pm.ConstantData('X_data', X)

    # pを確率変数でなく定数にした
    p = 0.5

    # s: 潜在変数　pの確率値をもとに0, 1のいずれかの値を返す
    s = pm.Bernoulli('s', p=p, shape=N)

    # mus: ２つの花の種類毎の平均値
    mus = pm.Normal('mus', mu=0.0, sigma=10.0, shape=n_components)

    # sigmas: 2つの花の種類毎のバラツキ
    sigmas = pm.HalfNormal('sigmas', sigma=10.0, shape=n_components)

    # 各観測値ごとに潜在変数から平均値と標準偏差を求める
    mu = pm.Deterministic('mu', mus[s])
    sigma = pm.Deterministic('sigma', sigmas[s])

    # 正規分布によりxの値を求める
    X_obs = pm.Normal('X_obs', mu=mu, sigma=sigma, observed=X_data)

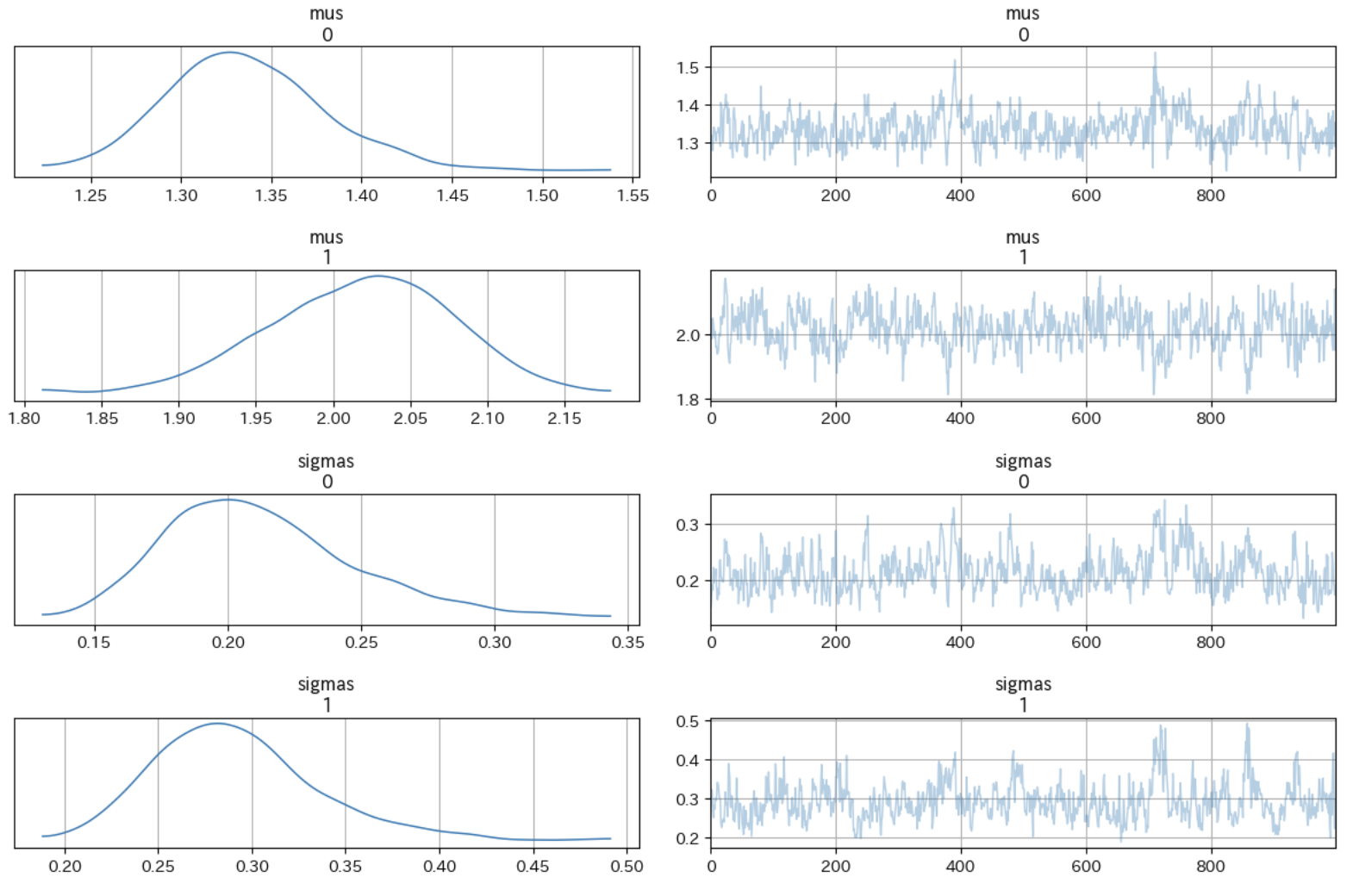
今度はpを0.5の固定値にした上で、pm.Normalをtauでなくsigmaの形で与えています。

サンプリング結果は次のようなきれいな形になりました。

この実験から一つわかることは、p=0.5固定値の簡略版潜在変数モデルであれば、通常のsigmaをパラメータにする形で問題なくベイス推論することは可能という話です。

では、なぜ書籍の難しい設定の確率モデルだとtauをパラメータにしないと安定した結果が得られないのか。
この点は完全に説明することはできないですが、一つの仮説として、sigmaを使った分布の場合、sigma=0に近づくと確率密度関数としては、特定の値に集中した不安定な分布になります。このような分布関数になってしまう可能性が高いからということが考えられます。