書籍「ディープラーニングの数学」10章のDLモデルをGPUで動かす

はじめに

書籍「ディープラーニングの数学」の著者です。

 Amazonリンク

この書籍は、ディープラーニングを含めた機械学習のアルゴリズムを数学的に定式化し、Pythonのプログラムをスクラッチで組み立てて(使っているライブラリはほぼNumPyとMayplotlibだけです)、実習コードで動作を確認する立て付けの本です。

10章の実習プログラムはディープラーニングのプログラムになっているのですが、他の章の実習コードと比べて恐ろしく処理に時間がかかります(1つの繰り返し処理で30分から1時間)。ここをなんとかできないかと前から思っていて、先日、ふと、生成AIに問いかけてみました。彼から返ってきた答えが、「PyTorchで組めばできます」というもの。

なるほど、私は PyTorchの入門書の書いているくらいで、基礎的なことはわかっているつもりですが、数値微分の仕組みを一切使わず、単に行列演算のエンジンとして使うことはできるわけで、そうすれば自分のやりたいことができることに気付きました。ありがとう、AIさんという感じです。

ということで、この記事は、「ディープラーニングの数学10章の実習プログラムをPytorchにより高速化したプログラム」のご紹介ということになります。

結論からいうと、この改修はうまくいきました。同じ条件で改修前のプログラムを動かした場合と比較して、処理時間は格段にあがりました。あとで説明するようにバッチサイズを小さくした関係で、より多くの繰り返し回数が必要になったのですが、12分で2000エポックの処理ができました。
精度も約98%まであがりました。これは、バッチサイズを変えた効果なのですが、書籍では隠れ層2階層のモデルでも実現できなかった精度です。

プログラムのリンク

最初にプログラムのリンクをご紹介します。

(実行結果付き)
https://github.com/makaishi2/math_dl_book_info/blob/master/sample-notebook/ch10_new_w_result.ipynb

(実行結果なし)
https://github.com/makaishi2/math_dl_book_info/blob/master/sample-notebook/ch10_new.ipynb

実は、本書の他の実習コードにも見直しをかけています。
全体のプログラム一覧のリンクはこちら
https://github.com/makaishi2/math_dl_book_info/tree/master/sample-notebook

7章の実習は、ボストンデータセットを使っているのですが、ご時世で、今やこのデータはデータ入手から難しくなっています。上のリンク先の7章の実習は、ボストンデータセットの代わりにカリフォルニアデータセットを使ったものになっています。

プログラム見直しにおける変更点

これから、ご紹介する実習プログラムは、元の書籍の実習コードと比べて、次の点に変更を加えています。

重み行列の初期値
書籍ではすべての要素に1を設定して、うまくいかないところから初めているのですが、検証コードではこの回りくどいことをスキップして、最初から乱数による初期設定をしています、

バッチサイズ
書籍では、512で実装しているのでは、今回は128に変更しました。これは、Pytorchの本を書いているときにこの方が精度が高くなることに気付いたからです。

繰り返し回数
書籍では100だったのですが、2000に増やしています。上のパラメータの場合、この値が最適になりそうだったからです。

この他、データ取得のコードなど、何カ所か見やすく直したところがあります。

Google ColabでのGPU利用

Google Colabでは、追加ライセンスなしに一定の制約の下でGPUが利用できます(あまり長い処理をすると時間切れになってしまう点が制約ですが、今回ご紹介したプログラムを動かす分には問題ないです)。
具体的な手順は下記ですが、上で紹介したnotebookを使う場合、notebook側の設定でGPUを選ぶようになっているので、下記の手順をマニュアルで設定する必要はないです。

ランタイムのタイプの変更

次の画面のように、Google Colabのnotebook画面から「ランタイム」「ランタイムのタイプを変更」を選択します。

次の画面になったら、「T4 GPU」を選択し、右下の「保存」をクリックします。

動作確認

次のコードで、動作を確認します。

import torch

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)

「cuda:0」と返ってきたら、設定が正しくできています。「cpu」の場合は、設定がおかしいので手順を再確認して下さい。

コード解説

ここからは、今回の実装でポイントになるコードを解説します。
要は今までNumPyでやっていた繰り返し計算をすべてPytorchのTensor型データを対象とし、torch.xxの関数だけを使って行うという話になります。

データ変更

NumPyからTensorへの変換

例えば、x_test_npがNumPyの変数だったとすると、次のコードで対応するTensor変数を作れます。

x_test = torch.Tensor(x_test_np).float()

cpuからgpuへの送付

cpu上のTensor変数をgpuに送付するためのコードは下記になります。
変数deviceは、上の動作確認のコードで'cuda:0'に値を設定済みであることに注意して下さい。

x_test_gpu = x_test.to(device)

GPU計算の方法

次の2つに注意します。

• 対象の2つのデータはともにGPU上にあること(片方しかないとランタイムエラーになります)
• 演算はすべてtorch.xxの関数と基本的な演算子のみから構成されていること

notebookのプログラム解説

ここからは、notenook上のプログラムを題材に解説します。

訓練データ・テストデータへの分割

from sklearn.model_selection import train_test_split
x_train_np, x_test_np,y_train_np, y_test_np,y_train_ohe_np, y_test_ohe_np = train_test_split(
    x_all, y_org, y_all_ohe, train_size=60000, test_size=10000, shuffle=False)

# 結果確認
print('訓練データ', x_train_np.shape, y_train_np.shape, y_train_ohe_np.shape)
print('テストデータ', x_test_np.shape, y_test_np.shape, y_test_ohe_np.shape)

オリジナルのnotebookとほぼ同じなのですが、変数名をx_test_npなど、_npのサフィックスを付けました。計算のメインの箇所ではすべての変数はTensorになるので、NumPyであることが区別付くようにとの理由からです。

データ変換

x_train = torch.Tensor(x_train_np).float()
y_train = torch.Tensor(y_train_np).float()
y_train_ohe = torch.Tensor(y_train_ohe_np).float()
x_test = torch.Tensor(x_test_np).float()
y_test = torch.Tensor(y_test_np).float()
y_test_ohe = torch.Tensor(y_test_ohe_np).float()

x_test_gpu = x_test.to(device)
y_test_gpu = y_test.to(device)
y_test_ohe_gpu = y_test_ohe.to(device)

上で説明したルールに従って、NumPy変数をTensor変数に変換します。
学習データに関しては、ここでGPUに送付してしまうとデータ量が大きくなってしまうので、繰り返し処理でバッチサイズ分の小さなデータに分割したタイミングで送付することにします。
逆にテストデータに関しては、同じデータを常に使い続けるので、この段階でGPUに送付してしまいます。

学習データの内容確認

N = 20
np.random.seed(12)
indexes = np.random.choice(y_test.shape[0], N, replace=False)
x_selected = x_test[indexes,1:]
y_selected = y_test[indexes]
plt.figure(figsize=(10, 3))
for i in range(N):
    ax = plt.subplot(2, int(N/2), i + 1)
    plt.imshow(x_selected[i].reshape(28, 28),cmap='gray_r')
    ax.set_title('%d' %y_selected[i], fontsize=16)
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
plt.show()

ここで、表示対象になっているx_testはTensor 型の変数なのですが、この状態でimshowによる画面表示はできるので(Pytorch本の実装コードで確認済み)、そのことを利用しています。

汎用関数

import torch.nn as nn
sigmoid = nn.Sigmoid()
softmax = nn.Softmax(dim=1)

def step(x):
    return ( x > 0).float()

def relu(x):
    return torch.where(x > 0, x, torch.tensor(0.0))

sigmoid関数とsoftmax関数はPyTorchの関数を利用します。
活性化関数にrelu関数も使いたくて、この関数定義もしているのですが、うまくいかなくて、これから紹介する実習コードでは結局使っていません。原因は今のところ不明です。

予測関数

def pred(x, W):
    return softmax(x @ W)

書籍の実習コードで、内積計算を演算子@で実装していることが自慢？でした。
PyTorch化でここは直す必要があるかと思ったのですが、結果的にそのままでOKでした。
同じことは、元の実装コードで何カ所か使っている「.T」(転置行列)にも言えて、最新版のPyTorchではそのままでOKです。

損失関数(交差エントロピー関数)

def cross_entropy(yt_ohe, yp_ohe):
    return -torch.mean(torch.sum(yt_ohe * torch.log(yp_ohe), dim=1))

PyTorchにも交差エントロピー関数はあるのですが、ちょっとクセがあり使いにくいので、単純な関数の組み合わせでスクラッチで定義しています。使っているtorch関数は、mean関数、sum関数、log関数と名前から動作が想像できるものばかりです。

evaluate関数(損失と精度を計算)

from sklearn.metrics import accuracy_score

def evaluate(x_test, y_test, y_test_ohe, x_dum, V, W):

    # テストデータに対して隠れ層の値を計算
    b_test = sigmoid(x_test @ V)

    # ダミー変数追加
    b1_test = torch.cat((x_dum, b_test), dim=1)

    # 予測値算出
    yp_test_ohe = softmax(b1_test @ W)

    # ラベル値算出
    yp_test = torch.argmax(yp_test_ohe, dim=1)

    # 損失計算(item関数でスカラー化)
    loss = cross_entropy(y_test_ohe, yp_test_ohe).item()

    # 精度計算()
    score = (y_test == yp_test).float().mean().item()

    return score, loss

ここが一番ややこしいところでした。
b_testの計算の後で実施しているb1_testの計算では、もともとnumpyのinsert関数を使ってダミー変数の追加をしています。PyTrochには該当する関数がなさそうなので、事前に

x_dum2 = torch.ones((len(x_test),1)).float().to(device)

というすべての要素が1の配列を準備し、GPUに送付しておきます。(この後で説明する初期化コードに含まれている)
この変数を引数で受け取った後、

b1_test = torch.cat((x_dum, b_test), dim=1)

とすることでnp.insert関数と同じ結果を得るようにしました。
この後の処理はコメントどおりのことをやっているので、コメント文を見ることで処理概要が理解できると思います。
1点だけ補足すると、損失計算と精度計算の最後で呼び出しているitem関数で、スカラー値をtensor型から、通常のflaot型に変更し、グラフ描画などができる形にしています。

初期化処理

# 隠れ層のノード数
H = 128
H1 = H + 1
# M: 訓練用系列データ総数
M  = x_train.shape[0]
# D: 入力データ次元数
D = x_train.shape[1]
# N: 分類クラス数
N = y_train_ohe.shape[1]

# 繰り返し回数
nb_epoch = 2000
# ミニバッチサイズ
batch_size = 128
B = batch_size
# 学習率
alpha_np = 0.01

# 重み行列の初期設定
np.random.seed(123)
V_np = np.random.randn(D, H) / np.sqrt(D / 2)
W_np = np.random.randn(H1, N) / np.sqrt(H1 / 2)

# 評価結果記録用 (損失関数値と精度)
history1 = np.zeros((0, 3))

# ミニバッチ用関数初期化
indexes = Indexes(M, batch_size)

# 繰り返し回数カウンタ初期化
epoch = 0

# GPU転送
alpha = torch.tensor(alpha_np).float().to(device)
V = torch.tensor(V_np).float().to(device)
W = torch.tensor(W_np).float().to(device)
x_dum = torch.ones((batch_size,1)).float().to(device)
x_dum2 = torch.ones((len(x_test),1)).float().to(device)

コードの前半部分は書籍のコードとまったく同一です。ただ、ミニバッチサイズは512から128に、繰り返し回数は100から2000に変更しています。

最後のGPU転送以下が、今回新たに追加したコードで、それぞれの変数をGPUに送付している部分となります。
x_dumとx_dum2は、上で説明したダミー変数用で、学習時と、精度評価時で、データサイズが異なるので、2種類準備しています。

繰り返し処理

%%time
while epoch < nb_epoch:

    # 学習対象の選択(ミニバッチ学習法)
    index, next_flag = indexes.next_index()

    # 学習対象選択時にGPU転送を行う
    x, yt = x_train[index].to(device), y_train_ohe[index].to(device)

    # 予測値計算 (順伝播)
    a = x @ V
    b = sigmoid(a)
    b1 = torch.cat((x_dum, b), dim=1)
    u = b1 @ W
    yp = softmax(u)

    # 誤差計算
    yd = yp - yt
    bd = b * (1-b) * (yd @ W[1:].T)

    # 勾配計算
    W = W - alpha * (b1.T @ yd) / B
    V = V - alpha * (x.T @ bd) / B

    if next_flag : # 1epoch 終了後の処理
        score, loss = evaluate(x_test_gpu, y_test_gpu, y_test_ohe_gpu, x_dum2, V, W)
        history1 = np.vstack((history1, np.array([epoch, loss, score])))
        epoch = epoch + 1
        if (epoch-1) % 10 == 0:
            print(f'epoch = {epoch-1} loss = {loss:.04f} score = {score:.04f}')

ポイントになるところを順番に説明します。

%%time

処理時間がわかるように冒頭に入れておきました。
手元の環境での実測値としては12分弱(繰り返し2000回)となっています。

x, yt = x_train[index].to(device), y_train_ohe[index].to(device)

学習データに関しては、ミニバッチ学習法で学習対象が決まるたびに、都度GPUに送付しています。

b1 = torch.cat((x_dum, b), dim=1)

精度評価の時と同じで、学習時もダミー変数はcat関数で追加するようにしています。

score, loss = evaluate(x_test_gpu, y_test_gpu, y_test_ohe_gpu, x_dum2, V, W)

評価関数呼び出し時のコードです。引数はすべてGPU上の変数となっています。

損失・精度確認

print(f'初期状態: 損失関数:{history1[0,1]:.04f} 精度:{history1[0,2]:.04f}')
print(f'最終状態: 損失関数:{history1[-1,1]:.04f} 精度:{history1[-1,2]:.04f}')

次のような結果で、最終精度は98%にやや届かない形でした。
しかし、書籍の結果と比べると、隠れ層2層のモデルよりいい精度です。

初期状態: 損失関数:2.4922 精度:0.1119
最終状態: 損失関数:0.0645 精度:0.9791

学習曲線(損失)

plt.figure(figsize=(6,6))
plt.plot(history1[:,0], history1[:,1], 'b')
plt.xlabel('繰り返し回数')
plt.ylabel('損失')
plt.title('学習曲線(損失)')
plt.grid()
plt.show()

次のような美しい学習曲線でした。

学習曲線(精度)

plt.figure(figsize=(6,6))
plt.plot(history1[:,0], history1[:,2], 'b')
plt.xlabel('繰り返し回数')
plt.ylabel('損失')
plt.title('学習曲線(精度)')
plt.grid()
plt.show()

こちらも美しい学習曲線です。

個別イメージ別の精度確認

N = 20
np.random.seed(12)
x_dum3 = torch.ones((N,1)).float().to(device)
indexes = np.random.choice(y_test.shape[0], N, replace=False)

# x_orgの選択結果表示 (白黒反転)
x_selected = x_test[indexes].to(device)
y_selected = y_test[indexes].to(device)

# 予測値の計算

# テストデータに対して隠れ層の値を計算
b_test = sigmoid(x_selected @ V)

# ダミー変数追加
b1_test = torch.cat((x_dum3, b_test), dim=1)

# 予測値算出
yp_test_ohe = softmax(b1_test @ W)

# ラベル値算出
yp_test = torch.argmax(yp_test_ohe, dim=1)

# グラフ表示
plt.figure(figsize=(10, 3))
for i in range(N):
    ax = plt.subplot(2, int(N/2), i + 1)
    plt.imshow(x_selected[i,1:].cpu().reshape(28, 28),cmap='gray_r')
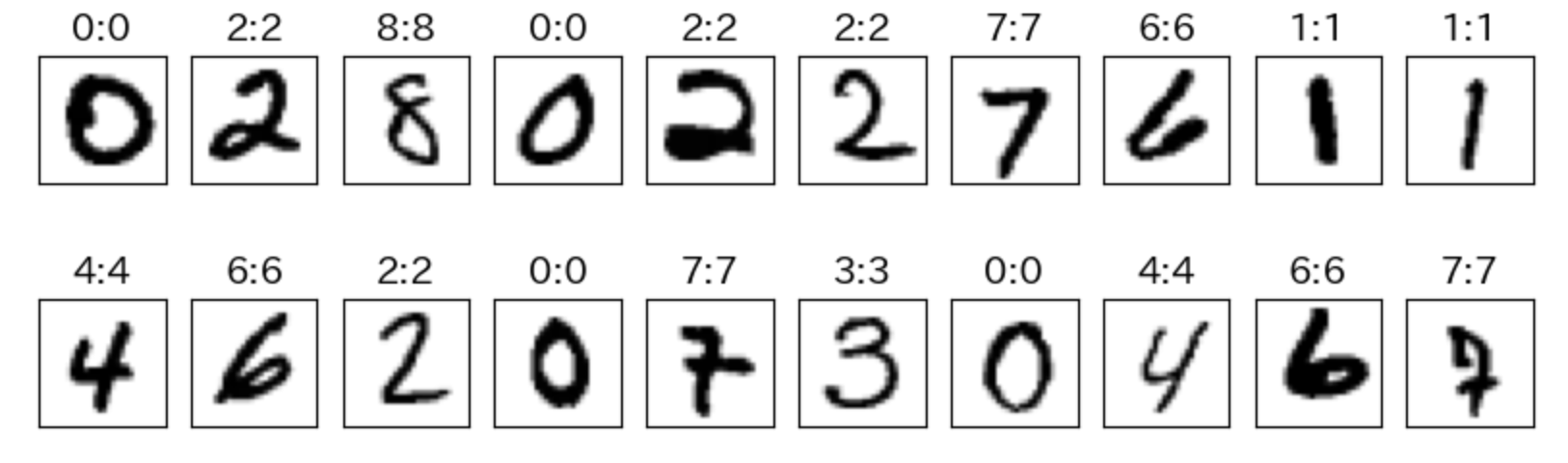
    ax.set_title('%d:%d' % (y_selected[i], yp_test[i]),fontsize=14 )
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
plt.show()

冒頭に20行分のダミー変数追加用のコードを足しています。それ以外のところは今まで説明したとおりです。
結果は下にあるとおりで、20文字すべて「正解」でした。