0. はじめに
ハフマン符号を学んだとき、実装には様々なデータ構造やアルゴリズムが必要だと思い、この記事にまとめました。できるだけたくさんのデータ構造やアルゴリズムを入れることを目標にしたので、コンパクトなものにはなっていませんので、その点はご承知ください。
以下のデータ構造とアルゴリズムを用いています。
- 可変長配列 std::vector
- 連想配列 std::map
- 2つの異なる型の値を保持する std::pair
- 複数の型の値を保持する std::tuple
- 優先度つきキュー std::priority_queue
- 深さ優先探索(depth first search : DFS)
1. ハフマン符号とは
ハフマン符号とは、文字をビット列(0と1の列)に変換する方法の一つです。
文字の出現頻度に応じて、出現頻度が大きいものは短いビット列、出現頻度が小さいものは長いビット列を当てはめることでデータ量を圧縮できる符号です。また、一度先頭からビット列を読むだけで一意に復号できる符号(接頭符号)です。
2. 符号化の方法
符号化は以下の手順で行います。
① 文字の出現頻度を求める
② ハフマン木を構成する
③ ハフマン木の各エッジに0と1を当てはめていく
④ ハフマン木の根から文字までのノードを辿ってできたビット列が符号語となる
また、ハフマン木は
②.① 各文字に対応するノードを1つずつ作る
②.② 親を持たないノードのうち、出現頻度が小さい2つのノードを選ぶ
②.③ その2つの出現頻度を足し合わせたノードを新たに作る
②.④ 新たなノードをその2つのノードの親とする
②.⑤ 2-4の手順を全てのノードがつながれるまで繰り返す
という手順で構成します。具体例を見てみましょう。
3. 符号化の具体例
文字列 "aaaabbbccd" を符号化してみましょう。
① 文字の出現頻度を求める
文字の種類は4種類で、その出現頻度は
- a は4回
- b は3回
- c は2回
- d は1回
となっています。
② ハフマン木を構成する
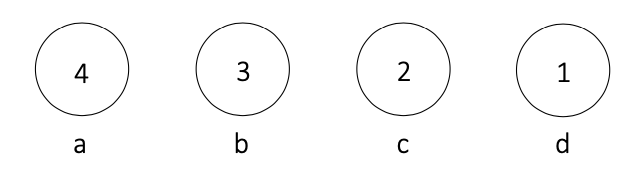
②.① 各文字に対応するノードを1つずつ作る
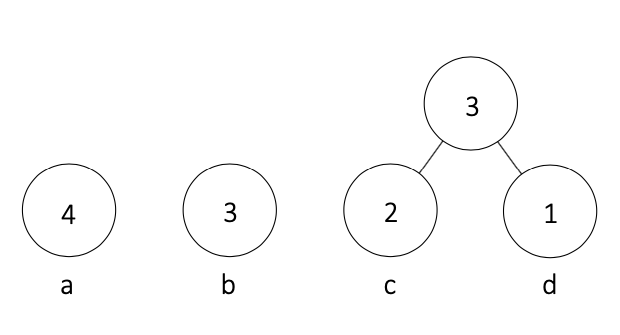
②.② 親を持たないノードのうち、出現頻度が小さい2つのノードを選ぶ
②.③ その2つの出現頻度を足し合わせたノードを新たに作る
②.④ 新たなノードをその2つのノードの親とする
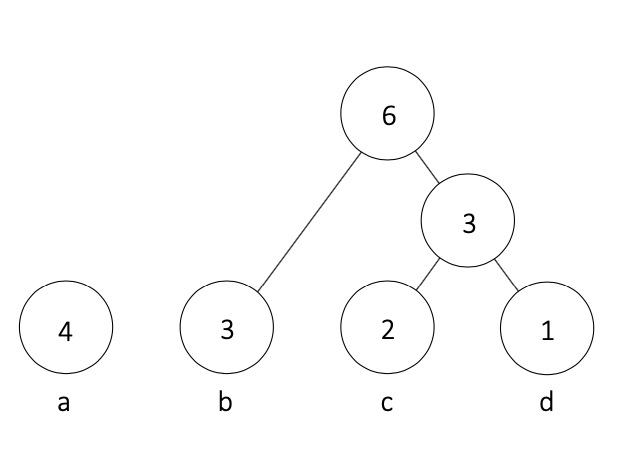
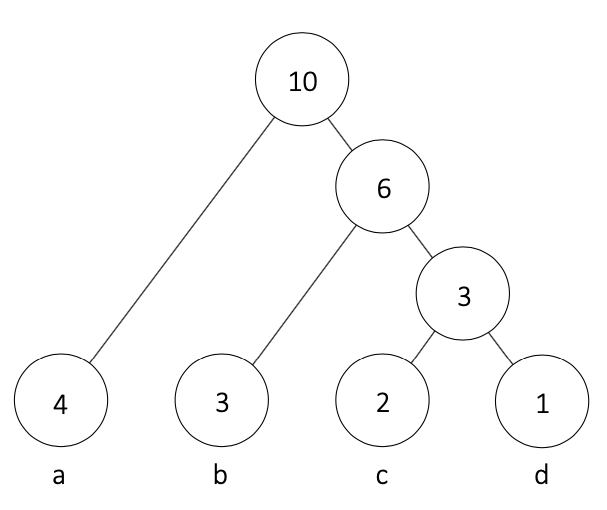
②.⑤ ②.②-②.④の手順を全てのノードがつながれるまで繰り返す
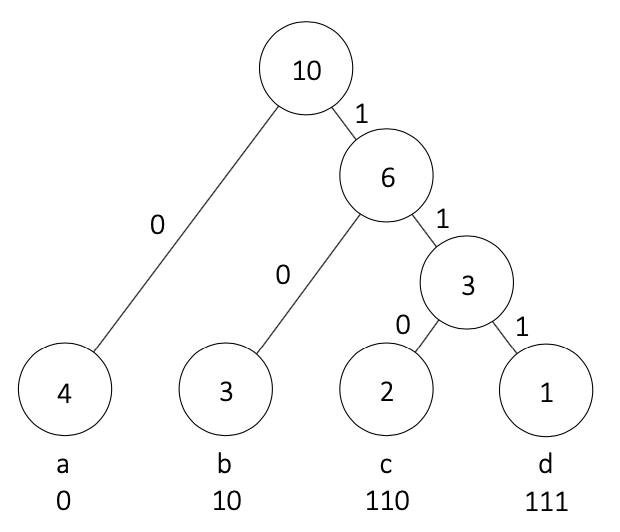
③ ハフマン木の各エッジに0と1を当てはめていく
④ ハフマン木の根から文字までのノードを辿ってできたビット列が符号語となる
以上のように、
- a は 0
- b は 10
- c は 110
- d は 111
が符号語となります。
これを用いると、
"aaaabbbccd" は、"0000101010110110111"
と符号化されました。
どのくらいデータが圧縮されたのか考えてみましょう。'a' や 'b' などはASCIIコードを用いて表されます。ASCIIコードは通常7bitで表されます。そのため変換前の文字列は、
10(文字)×7(bit/文字)=70(bit)
が必要です。一方、変換された後は、19bitとなっています。変換表を考慮してもかなり圧縮できています。
4. ハフマン符号の実装
ここからはハフマン符号を実装していきましょう。プログラミング言語はC++とします。
次のような問題を考えます。
【問題文】
文字列 $S$ が入力として与えられます。
ハフマン符号化を行ったとき、その変換表と変換後のビット列を出力するプログラムを作成してください。
【制約】
$S$ はアルファベットと数字、ピリオド
.、カンマ,、アンダーバー_からなる半角文字列である。
【入力】
入力は以下の形式で標準入力から与えられる。
$S$
【出力】
以下の形式で出力せよ。ただし、$N$は文字の種類の数、$A_i\ (0\leq i \leq M-1)\ $は文字、$B_i$は$A_i$に対応する符号語(ビット列)、$T$は$S$を変換した符号文字列である。また、$A_i$は辞書順に出力せよ。
$N$
$A_0$ $B_0$
$\vdots$
$A_{N-1}$ $B_{N-1}$
$T$
【入力例】
aaaabbbccd
【出力例】
4
a 0
b 10
c 110
d 111
0000101010110110111
4.1 「① 文字の出現頻度を求める」の実装
この実装にはC++のSTLである、連想配列 std::map というデータ構造を用いると簡単に実装できます。通常の配列では、数字のインデックス $i$ に対して1つの値が定まりますが、連想配列は数字だけでなく、文字や文字列、std::pair などあらゆる型に対して1つの値を定めることができます。std::mapでは、第1要素によって常にソートされています。そのため、出力の際にソートし直す必要がありません。
例えば、char型に対してint型の値が定められている連想配列distでは、アルファベット'a'の出現頻度が4回であることは、dist['a'] = 4と表すことができます。
これを実装に用いると、以下のようになります。関数の#include部とusing namespace stdは省略しています。
void get_distribution(string S, map<char, int> &dist){
for (int i = 0; i < (int) S.length(); i++) {
dist[S[i]]++;
}
}
4.2 「② ハフマン木を構成する」の実装
4.2.1 「②.① 各文字に対応するノードを1つずつ作る」の実装
ハフマン木はC++のSTLであるstd::vectorとstd::tupleを用いて実装できます。また、C言語からある構造体structでも実装できます。
std::vectorは、通常の配列std::arrayと異なり長さを変えることのできる可変長配列であり、std::tupleは、複数の型をまとめて格納できます。std::tupleに似た概念として、2つの型を同時に格納できるstd::pairもあります。
ハフマン木には、vector<tuple<int, vector<int>, string> > T(2*N-1)を用います。tupleの第1要素にそのノードを根とする部分木の出現頻度の和、第2要素には子ノードの番号、第3要素には対応するビット列を格納します。
void initialize_huffman_tree(map<char, int> &dist, vector<tuple<int, vector<int>, string> > &T){
int i = 0;
vector<int> temp = {};
for (auto itr : dist){
T[i] = make_tuple(dist[itr.first], temp, "");
i++;
}
}
4.2.2 「②.② 親を持たないノードのうち、出現頻度が小さい2つのノードを選ぶ」の実装
これは、C++のSTLであるstd::priority_queueを用いると簡単に実装できます。priority_queueは、優先度つきキュー(常にソートされており、簡単に取り出したい条件にあう要素を取り出せる)となっています。
priority_queueに第1要素が先程求めた出現頻度、第2要素がアルファベットのインデックスであるpairを入れておきます。priority_queueはデフォルトでは値が降順に取り出されるので、昇順に取り出されるようにします。
void initialize_priority_queue(map<char, int> &dist, priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > &pque){
int i = 0;
for (auto itr : dist){
pque.push(make_pair(itr.second, i));
i++;
}
}
4.2.3 「②.③-②.⑤ ハフマン木の構成」の実装
priority_queueから最初の2要素を取り出し、新たなノードとしてハフマン木に追加する手順を繰り返します。
void make_huffman_tree(map<char, int> &dist, vector<tuple<int, vector<int>, string> > &T, priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > &pque){
for (int i = (int) dist.size(); i < 2*dist.size()-1; i++){
pair<int, int> temp1 = pque.top();
pque.pop();
pair<int, int> temp2 = pque.top();
pque.pop();
pair<int, int> temp3 = make_pair(temp1.first+temp2.first, i);
pque.push(temp3);
vector<int> temp4 = {temp1.second, temp2.second};
T[i] = make_tuple(temp3.first, temp4, "");
}
}
4.3 「③・④ ハフマン木からの符号語の構成」の実装
ここまでで構成してきたハフマン木を用いて符号語の作成を行います。2つの子のうち出現頻度が大きいものに1を、小さいものに0を割り当てていきます。ここでは、グラフ理論における重要なアルゴリズムである深さ優先探索(width first search : DFS)を用います。DFSは、その名の通り、ノードが子を持たなくなるまで深く探索していくアルゴリズムである。実装にはよく再帰が用いられます。ここではDFSを用いていますが、幅優先探索(Breadth First Search : BFS)を使っても同じ結果が得られます。
void huffman_tree_dfs(vector<tuple<int, vector<int>, string> > &T, int v) {
vector<int> temp1 = {};
if (get<1>(T[v]) != temp1){
for (int i = 0; i < 2; i++) {
string temp2 = get<2>(T[v]) + (char) (i+'0');
int idx = get<1>(T[v])[i];
T[idx] = make_tuple(get<0>(T[idx]), get<1>(T[idx]), temp2);
huffman_tree_dfs(T, idx); //再帰
}
}
}
5. 解答例
最後に出力部を完成させます。N == 1 すなわち、文字の種類数が1種類のときは、ダミーの文字を入れてあげないとハフマン木を正しく構成することができません。その処理をこのコードでは入れています。また、tupleを用いたことで、構造体を用いた場合よりも少し複雑になってしまいました。
ここまでで実装したものをまとめると以下のようになります。
#include <iostream>
#include <string>
#include <vector>
#include <map>
#include <algorithm>
#include <queue>
#include "get_distribution.hpp"
#include "initialize_huffman_tree.hpp"
#include "initialize_priority_queue.hpp"
#include "make_huffman_tree.hpp"
#include "huffman_tree_dfs.hpp"
using namespace std;
int main(){
//入力
string S;
cin >> S;
//① 文字の出現頻度を求める
map<char, int> dist;
get_distribution(S, dist);
int N = dist.size();
//種類数が1の場合はダミーの文字を入れる必要がある
bool dummy_flag = false;
if (N == 1){
dummy_flag = true;
N++;
char dummy = (char) (S[0]+1);
dist[dummy] = 0;
}
//②.① 各文字に対応するノードを1つずつ作る
vector<tuple<int, vector<int>, string> > T(2*N-1);
initialize_huffman_tree(dist, T);
//②.② 親を持たないノードのうち、出現頻度が小さい2つのノードを選ぶ
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > pque;
initialize_priority_queue(dist, pque);
//②.③ その2つの出現頻度を足し合わせたノードを新たに作る
//②.④ 新たなノードをその2つのノードの親とする
//②.⑤ 2-4の手順を全てのノードがつながれるまで繰り返す
make_huffman_tree(dist, T, pque);
//③ ハフマン木の各エッジに0と1を当てはめていく
//④ ハフマン木の根から文字までのノードを辿ってできたビット列が符号語となる
huffman_tree_dfs(T, 2*N-2);
//出力
if (dummy_flag) N--;
cout << N << endl;
map<char, string> codeword;//符号語
int i = 0;
for (auto itr : dist){
if (i < N){
cout << itr.first << " " << get<2>(T[i]) << endl;
codeword[itr.first] = get<2>(T[i]);
i++;
}
}
for (int i = 0; i < (int) S.length(); i++){
cout << codeword[S[i]];
}
cout << endl;
return 0;
}
6. q元ハフマン符号について
「0」と「1」のみでなく「2」以上の文字を使う $q$ 元ハフマン符号の実装についての記事を書きました。こちらも読んでみてください。
q元ハフマン符号の実装
7. 参考にさせていただいたページ
本記事を書く際に参考にさせていただきました。本当にありがとうございました。
- [C++] STLの型の使い分け
- 厳選！C++ アルゴリズム実装に使える 25 の STL 機能【前編】
- レッドコーダーが教える、競プロ・AtCoder上達のガイドライン【中級編：目指せ水色コーダー！】
- DFS (深さ優先探索) 超入門！ 〜 グラフ・アルゴリズムの世界への入口 〜【前編】