0. はじめに
前回の記事でハフマン符号を取りあげたのですが、「0」と「1」のみでなく「2」以上の文字を使う $q$ 元ハフマン符号 $(2\leq q \leq 10)$ を実装したいと思い、試してみました。
$q > 10$ でも文字を用意すれば実装可能ですが、実装が煩雑だったためこの制約を付けました。
1. q元ハフマン符号とは?
ハフマン符号の符号化の手順の詳細については、
情報理論で学ぶアルゴリズムとデータ構造(ハフマン符号)
をご覧ください。
(2元)ハフマン符号では、出現頻度が低い2個のノードをまとめて新たなノードを1つ作っていましたが、 $q$ 元ハフマン符号 $(2\leq q \leq 10)$ は、出現頻度が低い $q$ 個のノードをまとめて新たなノードを1つ作ります。
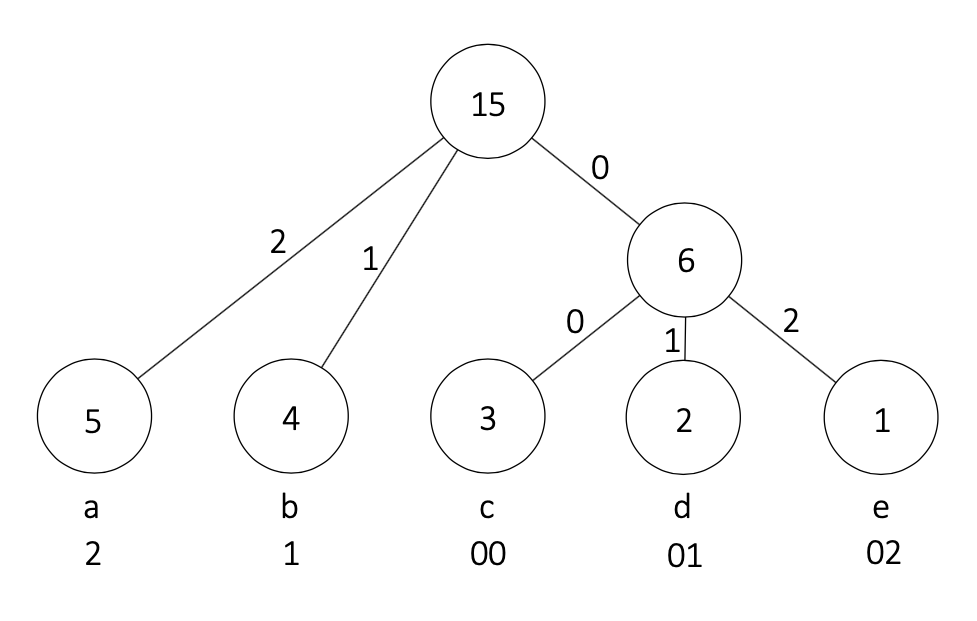
$q = 3$, $S = $"aaaaabbbbcccdde"の例で考えてみましょう。以下の図のようになります。ここでは、ノードの出現頻度が大きい順に0,1,2の順に数字を当てはめています。
2. ハフマン符号のダミー
実装は2元ハフマン符号を元に行いますが、2つの注意点があります。いずれもダミーのノードを追加する必要があります。詳しくは以下の章で説明していきます。
2.1. 文字種類数 N が q より小さいとき
この場合、$q$ 個をまとめることができないため、$q$ 元ハフマン木を構成することができません。
例として、 $q = 3, S = $"aab" ($N = 2$) のときが挙げられます。
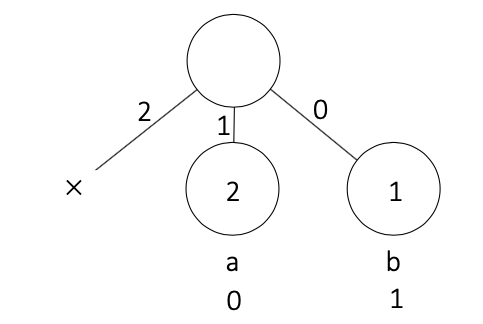
この場合は、出現頻度0のノード(ダミーのノード)を q - N 個追加すれば良いです。
2.2. 文字種類数 N を q-1 で割ったあまりが1ではないとき
これはどのような場合かというと、$q$ 個ずつノードをまとめていったとき、最後にノードが1つにまとまらない場合です。
例として、 $q = 3, S = $"aaaabbbccd" ($N = 4$) のときが挙げられます。$N=4$ を $q-1=2$ で割ったあまりは0であり、1ではありません。
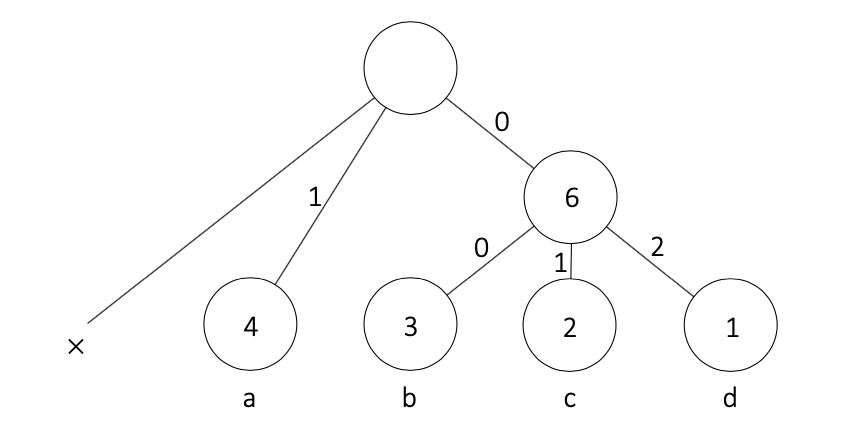
これはどのように導出されるかというと、「$q$ 個のノードをまとめて1つのノードにする」という操作を1回実行すると、ノードは $q$ 個減って1つ増えるので、合わせて $q-1$ 個減ることになります。$n$ 回 ($n \in \mathbb{N}$) 操作を行った後にノードが1つになって欲しいので、条件「ある自然数 $n$ に対して $N = (q-1) n + 1$」が必要になります。これを言い換えたものが2.2の条件「文字種類数 N を q-1 で割ったあまりが1である」となります。(2.2は2.1.の条件も含有していますが、あとで実装する際に $N=1$ での例外処理が必要になってしまうので分けています。)
この場合は、出現頻度0のノード(ダミーのノード)を (q-1) - (N-1)%(q-1) 個追加する必要があります。
3. q元ハフマン符号の実装
以上をもとに実装していきます。簡単のため、以下の問題で考えることにします。
【問題文】
整数 $q$ と文字列 $S$ が入力として与えられます。
$q$ 元ハフマン符号化を行ったとき、その変換表と変換後のビット列を出力するプログラムを作成してください。
【制約】
$q$ は $2\leq q \leq 10$をみたす。
$S$ はアルファベットと数字、ピリオド.、カンマ,、アンダーバー_からなる半角文字列である。
【入力】
入力は以下の形式で標準入力から与えられる。
$q\ \ \ S$
【出力】
以下の形式で出力せよ。ただし、$N$は文字の種類の数、$A_i\ (0\leq i \leq M-1)\ $は文字、$B_i$は$A_i$に対応する符号語(ビット列)、$T$は$S$を変換した符号文字列である。また、$A_i$は辞書順に出力せよ。
$N$
$A_0$ $B_0$
$\vdots$
$A_{N-1}$ $B_{N-1}$
$T$
【入力例】
3 aaaabbbccd
【出力例】
4 a 0 b 2 c 10 d 11 0000222101011
(2元)ハフマン符号と共通する部分が多いため、変更点だけを取りあげていきたいと思います。2元ハフマン符号の実装については、情報理論で学ぶアルゴリズムとデータ構造(ハフマン符号)
をご覧ください。
3.1. 全体の変更点
「① 文字の出現頻度を求める」に使ったdistや、符号語の保存に使ったcodewordのクラスである連想配列std::mapの第1要素をcharからstringへ変更しています。ダミーのノードを追加する際に、制約の範囲の文字のASCIIコードの最大値であるzよりも大きい文字である|を連ねたもの(例えば"||"など)を使うため、string型にする必要がありました。それに伴い、char型のS[i]をstring型のS.substr(i,1)に変更しています。また、関数の引数も少し変更しています。
3.2. ダミーのノードを追加する関数
2.1.と2.2.のダミーのノードの追加する操作を追加します。
int add_dummy_node(int &N, int q, map<string, int> &dist){
//2.1
int dummy_flag = (q-N > 0 ? q-N : 0);
//2.2
if (dummy_flag == 0) dummy_flag = ((N-1)%(q-1) ? (q-1) - ((N-1)%(q-1)) : 0);
if (dummy_flag){
N += dummy_flag;
string dummy;
for (int i = 0; i < dummy_flag; i++) {
dummy += '|';
dist[dummy] = 0;
}
}
return dummy_flag;
}
また、2元ハフマン符号では、合計ノード数は $2N-1$ 個でしたが、$q$ 元ハフマン符号では、$\frac{qN-1}{q-1}$ 個となります。そのため、ハフマン木を
vector<tuple<int, vector<int>, string> > T((q*N-1)/(q-1));に変更します。それに伴い、DFSで必要となるハフマン木の根のインデックスは(q*N-1)/(q-1)-1となります。
3.3. ハフマン木の構成・深さ優先探索の変更点
2元ハフマン符号ではforループは0...2を範囲としていましたが、$q$ 元では0...qを範囲にしています。
4. 実装例
# include <iostream>
# include <string>
# include <vector>
# include <map>
# include <algorithm>
# include <queue>
using namespace std;
void get_distribution(string S, map<string, int> &dist){
for (int i = 0; i < (int) S.length(); i++) {
dist[S.substr(i,1)]++;
}
}
int add_dummy_node(int &N, int q, map<string, int> &dist){
//2.1
int dummy_flag = (q-N > 0 ? q-N : 0);
//2.2
if (dummy_flag == 0) dummy_flag = ((N-1)%(q-1) ? (q-1) - ((N-1)%(q-1)) : 0);
if (dummy_flag){
N += dummy_flag;
string dummy;
for (int i = 0; i < dummy_flag; i++) {
dummy += '|';
dist[dummy] = 0;
}
}
return dummy_flag;
}
void initialize_huffman_tree(map<string, int> &dist, vector<tuple<int, vector<int>, string> > &T){
int i = 0;
vector<int> temp = {};
for (auto itr : dist){
T[i] = make_tuple(dist[itr.first], temp, "");
i++;
}
}
void initialize_priority_queue(map<string, int> &dist, priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > &pque){
int i = 0;
for (auto itr : dist){
pque.push(make_pair(itr.second, i));
i++;
}
}
void q_make_huffman_tree(int q, map<string, int> &dist, vector<tuple<int, vector<int>, string> > &T, priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > &pque){
unsigned long n = (q*dist.size()-1)/(q-1);
for (int i = (int) dist.size(); i < n; i++){
pair<int, int> temp1 = make_pair(0, i);
vector<int> temp2;
for (int j = 0; j < q; j++){
temp1.first += pque.top().first;
temp2.insert(temp2.begin(),pque.top().second);
pque.pop();
}
pque.push(temp1);
T[i] = make_tuple(temp1.first, temp2, "");
}
}
void q_huffman_tree_dfs(int q, vector<tuple<int, vector<int>, string> > &T, int v) {
vector<int> temp1 = {};
if (get<1>(T[v]) != temp1){
for (int i = 0; i < q; i++) {
string temp2 = get<2>(T[v]) + (char) (i+'0');
int idx = get<1>(T[v])[i];
T[idx] = make_tuple(get<0>(T[idx]), get<1>(T[idx]), temp2);
q_huffman_tree_dfs(q, T, idx); //再帰
}
}
}
int main(){
//入力
int q;
string S;
cin >> q >> S;
//① 文字の出現頻度を求める
map<string, int> dist;
get_distribution(S, dist);
int N = (int) dist.size();
//ダミーの文字を入れる
int dummy_flag = add_dummy_node(N, q, dist);
//②.① 各文字に対応するノードを1つずつ作る
vector<tuple<int, vector<int>, string> > T((q*N-1)/(q-1));
initialize_huffman_tree(dist, T);
//②.② 親を持たないノードのうち、出現頻度が小さい2つのノードを選ぶ
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > pque;
initialize_priority_queue(dist, pque);
//②.③ その2つの出現頻度を足し合わせたノードを新たに作る
//②.④ 新たなノードをその2つのノードの親とする
//②.⑤ 2-4の手順を全てのノードがつながれるまで繰り返す
q_make_huffman_tree(q, dist, T, pque);
//③ ハフマン木の各エッジに数字を当てはめていく
//④ ハフマン木の根から文字までのノードを辿ってできたビット列が符号語となる
q_huffman_tree_dfs(q, T, (q*N-1)/(q-1)-1);
//出力
if (dummy_flag) N -= dummy_flag;
cout << N << endl;
map<string, string> codeword;
int i = 0;
for (auto itr : dist){
if (i < N){
cout << itr.first << " " << get<2>(T[i]) << endl;
codeword[itr.first] = get<2>(T[i]);
i++;
}
}
for (int i = 0; i < (int) S.length(); i++){
cout << codeword[S.substr(i,1)];
}
cout << endl;
return 0;
}
5. 参考にさせていただいたページ
本記事を書く際に参考にさせていただきました。本当にありがとうございました。