問題:2つの円の交点を数値計算で求める
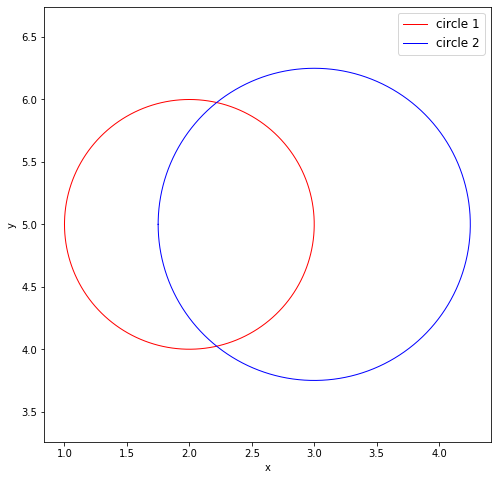
下図のように2つの円とその交点がある場合、交点を2次元のニュートン法で求める方法をご紹介します。
半径$r$、x軸方向オフセット$a$、y軸方向オフセット$b$の円は、媒介変数$\theta$を用いて次式で表せます。
$$
円の方程式\begin{cases}
x = r cos(\theta) + a \
y = r sin(\theta) + b
\end{cases}
$$
考える円は2つありますので、円1と円2の係数をそれぞれ添字の1と2、媒介変数を$\theta$と$\phi$で区別することにします。
$$
円1の方程式\begin{cases}
x_1 = r_1 cos(\theta) + a_1 \
y_1 = r_1 sin(\theta) + b_1
\end{cases}
$$
$$
円2の方程式\begin{cases}
x_2 = r_2 cos(\phi) + a_2 \
y_2 = r_2 sin(\phi) + b_2
\end{cases}
$$
よくあるニュートン法の計算例は1次元(1変数関数)ですが、この場合ですと、$\theta$と$\phi$の2つの変数がありますので2次元ニュートン法の計算を行います。
2つの円をプロットする
円の関数circleを定義して、円の軌跡データを作成し、matplotlibでプロットするPythonコードです。
import numpy as np
import matplotlib.pyplot as plt
def circle(theta, coeffs):
r = coeffs[0] # 半径r
a = coeffs[1] # x軸方向のオフセットa
b = coeffs[2] # y軸方向のオフセットb
x = r * np.cos(theta) + a
y = r * np.sin(theta) + b
return x, y
def plot_two_circle(circle_traj1, circle_traj2):
plt.figure(figsize=(8,8))
plt.axes().set_aspect('equal', 'datalim')
plt.plot(circle_traj1[0], circle_traj1[1], c='red', linewidth=1, label='circle 1')
plt.plot(circle_traj2[0], circle_traj2[1], c='blue', linewidth=1, label='circle 2')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='upper right', fontsize=12)
coeffs1 = (1.0, 2.0, 5.0) # 円1の係数 r=1.0 a=2.0 b=5.0
coeffs2 = (1.25, 3.0, 5.0) # 円1の係数 r=1.25 a=3.0 b=5.0
angle_range = np.linspace(-np.pi, np.pi, 501) # 501点の-pi ~ piの等間隔な配列を作る
circle_traj1 = circle(angle_range, coeffs1)
circle_traj2 = circle(angle_range, coeffs2)
plot_two_circle(circle_traj1, circle_traj2)
plt.show()
このコードを実行すると冒頭でお見せした2つの円の図が描画できます。
媒介変数の範囲は$-\pi~\pi$、円の半径$r$とオフセット$a,b$は適当な値を代入しました。
2次元ニュートン法のアルゴリズムフロー
2次元ニュートン法の計算手順をSTEP 1 ~ STEP 4に分けて説明します。
STEP 1. fxとfyを定義する
2つの円の交点は$x_1 = x_2$かつ$y_1 = y_2$を満たす点ですので、次式を満たす$x$と$y$が求める解になります。
$$
\begin{cases}
x_1 - x_2 = 0 \
y_1 - y_2 = 0
\end{cases}
$$
よって次のように新たな関数$f_x$と$f_y$を定義します。$f_x$と$f_y$は$\theta$と$\phi$の2変数で決定しますので、$f_x = f_x(\theta, \phi)$、$f_y = f_y(\theta, \phi)$で表せます。
$$
\begin{cases}
f_x(\theta, \phi) = x_1 - x_2 \
f_y(\theta, \phi) = y_1 - y_2
\end{cases}
$$
添字を区別して先ほど定義した円1の方程式と円2の方程式を代入すると次式となります。
$$
\begin{cases}
f_x(\theta, \phi) = r_1 cos(\theta) + a_1 - (r_2 cos(\phi) + a_2) \
f_y(\theta, \phi) = r_1 sin(\theta) + b_1 - (r_2 sin(\phi) + b_2)
\end{cases}
$$
STEP 2. fxとfyをベクトルで表現する
さらに、$f_x$と$f_y$をベクトル表記にします。
$$ \mathbf{f}(\boldsymbol{\psi}) =
\begin{bmatrix}
f_x(\theta, \phi) \
f_y(\theta, \phi)
\end{bmatrix}
$$
ここで、媒介変数$\theta, \phi$の2つを合わせてベクトル$\boldsymbol \psi = (\theta, \phi)$とします。
STEP 3. ψの変化が目標精度に達成するまで繰り返し計算する
媒介変数$\theta, \phi$に適当な初期値$\theta_0,\phi_0$を与えて、次式を繰り返し計算します。
$$
\boldsymbol \psi_0 =
\begin{bmatrix}
\theta_0 \
\phi_0
\end{bmatrix}, \
\boldsymbol \psi_{k+1} = \boldsymbol \psi_k - J(\boldsymbol \psi_k)^{-1} \mathbf{f}(\boldsymbol \psi_k)
$$
ここで、$k$は繰り返し計算の連番で$k = 0, 1, 2, ...$です。
$J(\boldsymbol \psi_k)^{-1}$は逆ヤコビアンでして、次式で定義されます。
$$
J(\boldsymbol \psi_k)^{-1} =
\begin{bmatrix}
J_{11} & J_{12} \
J_{21} & J_{22}
\end{bmatrix} ^{-1}
$$
$$
\begin{cases}
J_{11} = \frac{\partial f_x(\theta, \phi)}{\partial \theta} \
J_{12} = \frac{\partial f_x(\theta, \phi)}{\partial \phi} \
J_{21} = \frac{\partial f_y(\theta, \phi)}{\partial \theta} \
J_{22} = \frac{\partial f_y(\theta, \phi)}{\partial \phi}
\end{cases}
$$
今回の問題ですと、$f_x$と$f_y$を偏微分して$J$は次のようになります。
$$
\begin{cases}
J_{11} = \frac{\partial f_x(\theta, \phi)}{\partial \theta} = -r_1 sin(\theta) \
J_{12} = \frac{\partial f_x(\theta, \phi)}{\partial \phi} = r_2 sin(\phi) \
J_{21} = \frac{\partial f_y(\theta, \phi)}{\partial \theta} = \ r_1 cos(\theta) \
J_{22} = \frac{\partial f_y(\theta, \phi)}{\partial \phi} = -r_2 cos(\phi)
\end{cases}
$$
初期値の$\boldsymbol \psi_0$から$J(\boldsymbol \psi_0)^{-1} \mathbf{f}(\boldsymbol \psi_0)(=\Delta)$を計算し、$\boldsymbol \psi_1 = \boldsymbol \psi_0 - \Delta$を計算します。
同様に、$\boldsymbol \psi_1$から$\boldsymbol \psi_2$を計算します。
$\Delta$が目標精度$\epsilon [rad]$より小さくなるまで繰り返し計算します。
$\epsilon$は1e-3(=0.001)や1e-6(=0.000001)など求めたい精度に応じて決めておきます。
STEP 4. 解x, yを計算する
$k = n$で繰り返し計算が終了したとして、得られた解$\boldsymbol \psi_n = (\theta_n, \phi_n)$から$x, y$を計算します。円の方程式1を使用する場合は$\theta_n$のみ使用します。
$$
円の方程式1より求める解\begin{cases}
x = r_1 cos(\theta_n) + a_1 \
y = r_1 sin(\theta_n) + b_1
\end{cases}
$$
2次元ニュートン法の実装
媒介変数をベクトル表記した$\mathbf{f}(\boldsymbol{\psi})$をfxfy関数に定義します。
また、ヤコビアン$J$をjacobian関数に定義します。
def fxfy(psi, coeffs1, coeffs2):
theta, phi = psi
x1, y1 = circle(theta, coeffs1)
x2, y2 = circle(phi, coeffs2)
fx = x1 - x2
fy = y1 - y2
return np.array([fx, fy])
def jacobian(psi, coeffs1, coeffs2):
theta, phi = psi
r1 = coeffs1[0]
r2 = coeffs2[0]
J11 = -r1 * np.sin(theta)
J12 = r2 * np.sin(phi)
J21 = r1 * np.cos(theta)
J22 = -r2 * np.cos(phi)
return np.array([[J11, J12], [J21, J22]])
どちらも、上述しましたアルゴリズムフローの内容をそのまま実装しています。
続いて、ニュートン法の繰り返し計算部分を実装します。
# newton method
psi = np.array([0.25*np.pi, 0.5*np.pi]) # initial value of psi
eps = 1e-3 # convergence precision
delta = np.array([1e9, 1e9]) # initial value of inv(J)*f
k = 0 # index of loop
points = [] # store the solution
while (abs(delta[0]) > eps and abs(delta[1]) > eps):
try:
J = jacobian(psi, coeffs1, coeffs2)
invJ = np.linalg.inv(J)
f = fxfy(psi, coeffs1, coeffs2)
delta = np.dot(invJ, f)
psi = psi - delta
except:
print('could not calculate inverse J')
print('J = ')
print(J)
break
p = circle(psi[0], coeffs1)
points.append(p)
print('k = %s:' % k)
print(' (dtheta, dphi) = (%f, %f)' % (delta[0], delta[1]))
print(' (theta, phi) = (%f, %f)' % (psi[0], psi[1]))
print(' (x, y) = (%f, %f)' % (p[0], p[1]))
k += 1
if (k > 30):
print('could not convergence')
break
初期値$\boldsymbol \psi_0$、目標精度$\epsilon$の定義から始まり(それぞれpsiとeps)、目標精度に達するまで$\Delta$(delta)を繰り返し計算しています。計算結果の$x,y$をpointsに蓄積します。
$\boldsymbol \psi_0$の設定次第で、numpy.linalg.invがExceptionとなりますので、その場合はループを抜けて終了します。例えば$\theta_0 = \phi_0$の場合は逆行列が計算できません。
$k = 30$を超えても収束しない場合もループを抜けて終了します。
計算がうまく収束する場合は、$\epsilon = 1e-6$でしたら$k = 4,5$ほどで計算が終了します。
計算結果
繰り返し計算した解$x,y$をプロットします。
# plot solution
def draw_solution(solution):
px = np.array(solution).transpose()[0]
py = np.array(solution).transpose()[1]
plt.scatter(px, py, s=50, marker='+', c='limegreen', label='solution')
plt.legend(loc='upper right', fontsize=12)
for i in range(len(px)):
plt.text(px[i], py[i], 'k=' + str(i), size=12, c='black')
plot_two_circle(circle_traj1, circle_traj2)
draw_solution(points)
plt.show()
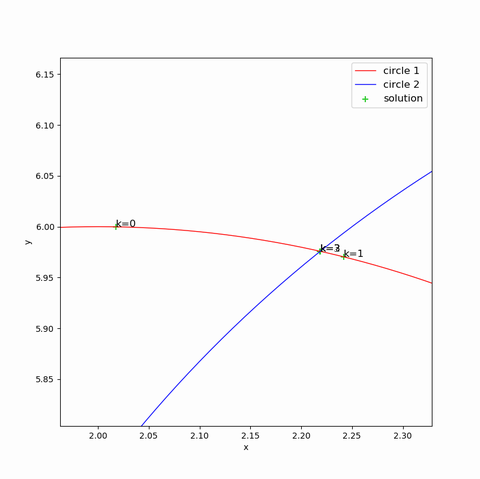
これまでのPythonスクリプトを実行すると次のグラフを得ます。
交点を緑色の十字マークで表しています。
この計算例では、4回の繰り返しで計算が終了しており、$k=0,1,2,3$の各交点を描画しています。
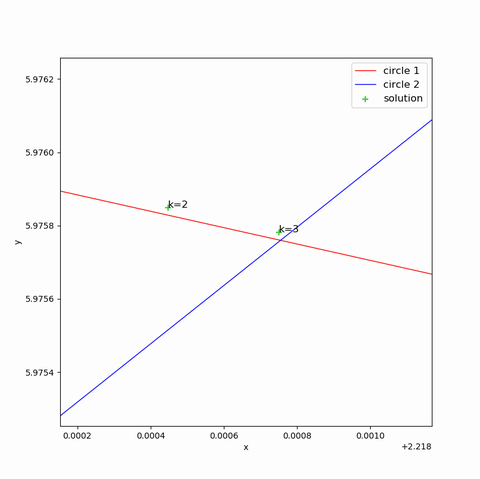
交点周辺を拡大すると下図のようになります。
$k=0,1,2,3$と計算が進むにつれて、数値計算解(緑色の十字マーク)が真の解(赤い線と青い線の交点)に近づく様子がおわかりになると思います。
計算過程で出力する記録は次のようになりました。
k = 0:
(dtheta, dphi) = (-0.767767, -0.668629)
(theta, phi) = (1.553165, 2.239425)
(x, y) = (2.017630, 5.999845)
k = 1:
(dtheta, dphi) = (0.226517, 0.019372)
(theta, phi) = (1.326648, 2.220054)
(x, y) = (2.241730, 5.970344)
k = 2:
(dtheta, dphi) = (-0.023925, -0.025854)
(theta, phi) = (1.350574, 2.245908)
(x, y) = (2.218447, 5.975849)
k = 3:
(dtheta, dphi) = (0.000311, -0.000020)
(theta, phi) = (1.350263, 2.245928)
(x, y) = (2.218750, 5.975781)
$k=0,1,2,3$と進むごとに$\Delta$(= delta = (dtheta, dphi))が小さくなり、$\epsilon = 1e-3 [rad]$より小さくなり繰り返し計算を終了しています。
おわりに
2次元ニュートン法による2つの円の交点の計算例をご紹介しました。
初期値を変えることでもう一方の交点も求めることができます。
また、円に関わらず大抵の2変数関数は2次元ニュートン法で求めることができます。うまく収束しない場合もありますのでご注意ください。
最後にこれまでのコードをまとめて終わりにします。
Pythonスクリプトまとめ
import numpy as np
import matplotlib.pyplot as plt
def circle(theta, coeffs):
r = coeffs[0] # 半径r
a = coeffs[1] # x軸方向のオフセットa
b = coeffs[2] # y軸方向のオフセットb
x = r * np.cos(theta) + a
y = r * np.sin(theta) + b
return x, y
def plot_two_circle(circle_traj1, circle_traj2):
plt.figure(figsize=(8,8))
plt.axes().set_aspect('equal', 'datalim')
plt.plot(circle_traj1[0], circle_traj1[1], c='red', linewidth=1, label='circle 1')
plt.plot(circle_traj2[0], circle_traj2[1], c='blue', linewidth=1, label='circle 2')
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc='upper right', fontsize=12)
def fxfy(psi, coeffs1, coeffs2):
theta, phi = psi
x1, y1 = circle(theta, coeffs1)
x2, y2 = circle(phi, coeffs2)
fx = x1 - x2
fy = y1 - y2
return np.array([fx, fy])
def jacobian(psi, coeffs1, coeffs2):
theta, phi = psi
r1 = coeffs1[0]
r2 = coeffs2[0]
J11 = -r1 * np.sin(theta)
J12 = r2 * np.sin(phi)
J21 = r1 * np.cos(theta)
J22 = -r2 * np.cos(phi)
return np.array([[J11, J12], [J21, J22]])
def draw_solution(solution):
px = np.array(solution).transpose()[0]
py = np.array(solution).transpose()[1]
plt.scatter(px, py, s=50, marker='+', c='limegreen', label='solution')
plt.legend(loc='upper right', fontsize=12)
for i in range(len(px)):
plt.text(px[i], py[i], 'k=' + str(i), size=12, c='black')
# make dataset
coeffs1 = (1.0, 2.0, 5.0) # 円1の係数 r=1.0 a=2.0 b=5.0
coeffs2 = (1.25, 3.0, 5.0) # 円1の係数 r=1.25 a=3.0 b=5.0
angle_range = np.linspace(-np.pi, np.pi, 501) # 501点の-pi ~ piの等間隔な配列を作る
circle_traj1 = circle(angle_range, coeffs1)
circle_traj2 = circle(angle_range, coeffs2)
# 2d newton method
psi = np.array([0.25*np.pi, 0.5*np.pi]) # initial value of psi
eps = 1e-3 # convergence precision
delta = np.array([1e9, 1e9]) # initial value of inv(J)*f
k = 0 # index of loop
points = [] # store the solution
while (abs(delta[0]) > eps and abs(delta[1]) > eps):
try:
J = jacobian(psi, coeffs1, coeffs2)
invJ = np.linalg.inv(J)
f = fxfy(psi, coeffs1, coeffs2)
delta = np.dot(invJ, f)
psi = psi - delta
except:
print('could not calculate inverse J')
print('J = ')
print(J)
break
p = circle(psi[0], coeffs1)
points.append(p)
print('k = %s:' % k)
print(' (dtheta, dphi) = (%f, %f)' % (delta[0], delta[1]))
print(' (theta, phi) = (%f, %f)' % (psi[0], psi[1]))
print(' (x, y) = (%f, %f)' % (p[0], p[1]))
k += 1
if (k > 30):
print('could not convergence')
break
# plot solution
plot_two_circle(circle_traj1, circle_traj2)
draw_solution(points)
plt.show()
![]() Happy Advent Calendar 2020
Happy Advent Calendar 2020![]()