【ポケポケ】ダークライとギラティナが揃う確率求めてみた！

背景

『Pokémon Trading Card Game Pocket（ポケポケ）』において、ダークライ・ギラティナデッキは、再現性、火力、耐久力の高さから長らく環境に居座り続けています。ギラティナが登場した2025/3/27（A2b「シャイニングハイ」）以降、記事投稿日の2025/9/21（A4a「未知なる水域」）においても、ランクマッチで安定して見かけるデッキの1つです。

このデッキの理想的な動きは、

• 1ターン目までにギラティナを場に出し、ターンの終了時に特性「はくうのさけび」を使うこと
• 後攻1ターン目または先行2ターン目までにダークライを場に出し、エネルギーを貼って特性「ナイトメアオーラ」を発動させること

で、この2つを満たせばかなり勝ちに近づきます。
では実際に、両方揃う確率はどのくらいなのでしょうか？

確率計算の方法

@ねぼすけAIさんの記事のように、カード効果を既存の確率分布（幾何分布・二項分布・多項分布・超幾何分布など）に対応づけることができれば、特定の場面での発生確率を数式で厳密に計算できます。しかし、「初期手札の5枚に加え、ターン開始時に1枚引き、さらに博士の研究やモンスターボールを複数回使用した後」となると、状況の分岐が爆発的に増加し、単純な数式で解くことは非常に困難になります。

このような複雑な確率を計算する手法として、主に以下の2つが挙げられます。

1. モンテカルロシミュレーション
   　乱数を用いて何万回も試行し、その結果から確率を推定する方法です。
   　概算を早く得られる反面、試行回数に依存して誤差が生じます。
2. 確率分布の全探索シミュレーション
   　初期手札・山札の組み合わせごとの確率を保持し、
   　カード効果を使うたびに状態を分岐させて確率を逐次更新していく方法です。
   　理論的に正確な確率が得られる一方で、計算量が膨大になりがちです。

今回は、この2つ目の確率分布の全探索シミュレーションを用いて、理想の盤面を作れる確率を厳密に計算します。プログラムの全体は記事末尾の使用したプログラムに掲載しています。

シミュレーションの条件

今回計算に用いるデッキは、以下の20枚です。（図1は該当するデッキの一例です）

• ダークライ：2枚
• ギラティナ：2枚
• 博士の研究：2枚
• モンスターボール：2枚
• その他（たねポケ以外）：12枚

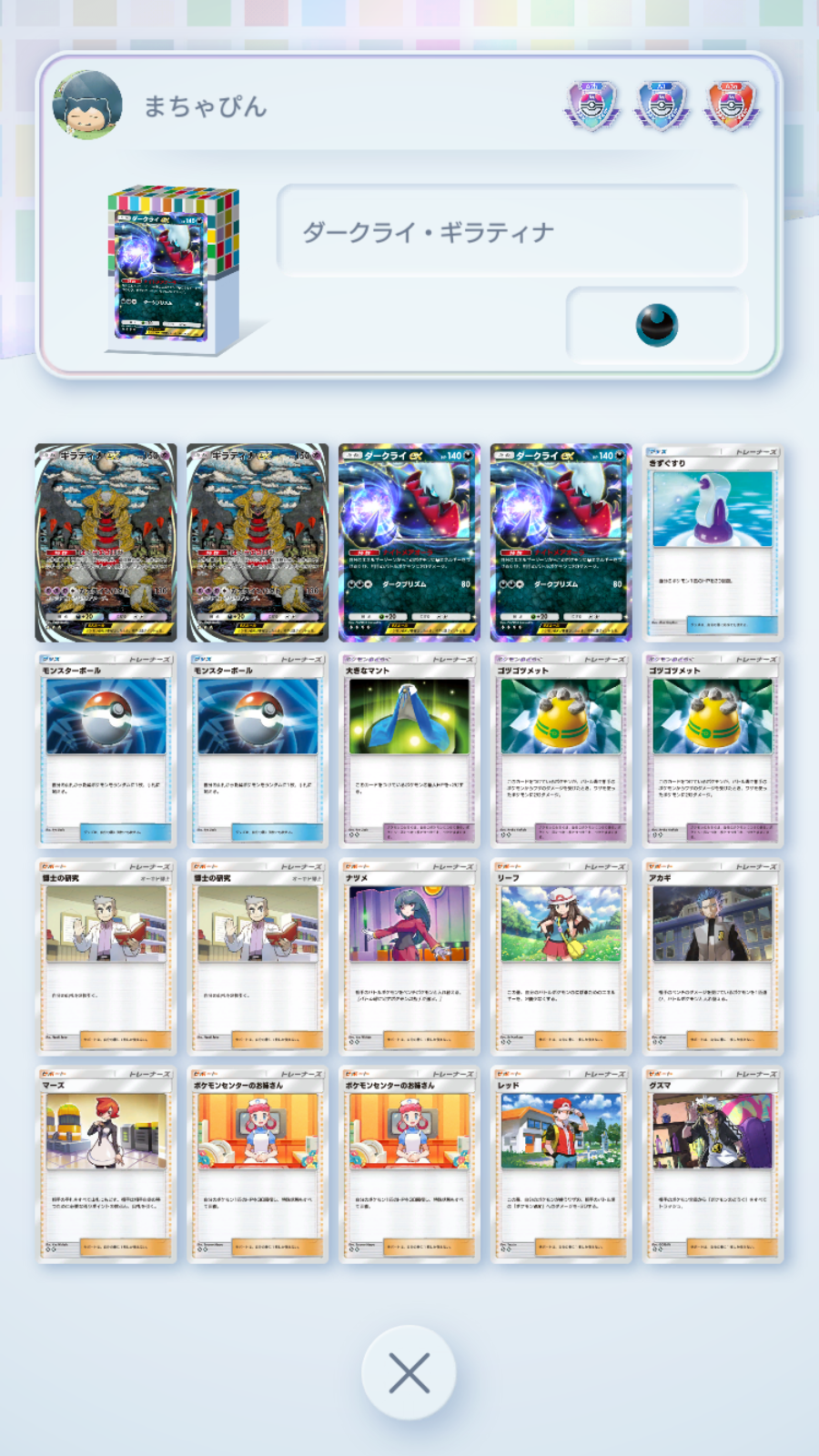
図1. 今回計算に用いるデッキの一例（ダークライ2枚、ギラティナ2枚、モンボ2枚、博士2枚、その他（たねポケ以外）12枚）

求める確率

以下の3つの状況における、手札の揃い方の確率を求めます。

状況	ダークライのみ	ギラティナのみ	ダークライ + ギラティナ
初期手札	➀	➁	➂
1T目終了時	➃	➄	➅
2T目終了時	➆	➇	➈

この表が示す確率は、それぞれ以下に対応します。

• ➂：バトル開始時に、ダークライとギラティナのどちらをバトル場に出すか選べる確率
• ➄+➅：1ターン目に、ギラティナの「はくうのさけび」を使える確率
• ➃+➅：後攻1ターン目に、ダークライの「ナイトメアオーラ」を発動できる確率
• ➆+➈：先行2ターン目に、ダークライの「ナイトメアオーラ」を発動できる確率
• ➅：後攻1ターン目に、ギラティナの「はくうのさけび」を使い、かつダークライの「ナイトメアオーラ」を発動できる確率
• ➄+➅-➇：先行1ターン目に、ギラティナの「はくうのさけび」を、先行2ターン目にダークライの「ナイトメアオーラ」を発動できる確率

なお、各行の確率を横方向に足すと、すべて100%になります。

初期手札における確率

@前回の記事より、初期手札のたねポケが1枚以上含まれるロジックは、山札から引いた5枚の中にたねポケが含まれなかった場合、手札の1枚を山札のたねポケ1枚と入れ替えることが仮説検定により明らかとなったため、このロジックを実装し計算を行います。

初期手札における確率は以下のようになりました。

状況	ダークライのみ	ギラティナのみ	ダークライ + ギラティナ
初期手札	41.18 %	41.18 %	17.65 %

注目すべきは、初期手札の5枚でダークライとギラティナが両方揃う確率は、わずか17.65%しかないという点です。ほとんどの場合はどちらか片方だけでスタートすることになり、相手のエネルギーの種類によってバトル場に出す方を選択できる場合は稀です。
しかし、この結果から、「初動がどちらからでも強い」ことがこのデッキの強さの所以であると考えることもできます。

1ターン目終了時における確率

1ターン目に「博士の研究」と「モンスターボール」をどちらを先に使うかで確率が変わるため、以下の2パターンで計算します。

1. 「博士の研究」を先に使う場合
2. 「モンスターボール」を先に使う場合

「博士の研究」を先に使う場合

1ターンの処理は、以下のように行います。

dist = apply_draw(dist)          # ドロー
dist = apply_professor(dist)     # 博士
dist = apply_monster_ball(dist)  # モンボ1枚目
dist = apply_monster_ball(dist)  # モンボ2枚目

それぞれの状況における確率は以下のようになりました。

状況	ダークライのみ	ギラティナのみ	ダークライ + ギラティナ
初期手札	41.18 %	41.18 %	17.65 %
1T目 ドロー後	35.69 %	35.69 %	28.63 %
1T目 博士後	30.52 %	30.52 %	38.96 %
1T目 モンボ1枚目後	16.83 %	16.83 %	66.34 %
1T目 モンボ2枚目後	15.84 %	15.84 %	68.32 %

初期手札でダークライとギラティナが揃う確率はわずか17.65%でしたが、1ターン目終了時に両方のポケモンが揃う確率は68.32%と急上昇します。特にこのデッキは、たねポケがダークライとギラティナの4枚しかないため、手札にたねポケが1枚しかない場合でも、「モンスターボール」を使用することでもう片方のたねポケを$2/3$で引くことが可能です。
この、たねポケの枚数が少ないことによる「再現性の高さ」が、このデッキの強さの所以であると考えることができます。

「モンスターボール」を先に使う場合

1ターンの処理は、以下のように行います。「博士の研究」により「モンスターボール」を2枚引く可能性があるため、再度apply_monster_ballを2回適用しています。

dist = apply_draw(dist)          # ドロー
dist = apply_monster_ball(dist)  # モンボ1枚目
dist = apply_monster_ball(dist)  # モンボ2枚目
dist = apply_professor(dist)     # 博士
dist = apply_monster_ball(dist)  # モンボ1枚目（博士で引いたモンボを使用）
dist = apply_monster_ball(dist)  # モンボ2枚目（博士で引いたモンボを使用）

それぞれの状況における確率は以下のようになりました。

状況	ダークライのみ	ギラティナのみ	ダークライ + ギラティナ
初期手札	41.18 %	41.18 %	17.65 %
1T目 ドロー後	35.69 %	35.69 %	28.63 %
1T目 モンボ1枚目後	22.30 %	22.30 %	55.40 %
1T目 モンボ2枚目後	21.46 %	21.46 %	57.07 %
1T目 博士後	18.06 %	18.06 %	63.88 %
1T目 モンボ1枚目後	16.06 %	16.06 %	67.88 %
1T目 モンボ2枚目後	16.03 %	16.03 %	67.94 %

1ターン目終了時に両方揃う確率は、「博士の研究」を先に使った方が、0.38%高いという結果になりました。しかし、その差は微々たるものであり、思っていたほど大きな変化はないというのが正直な感想です。
このプレイングの差が出る状況は、1ターン目ドロー後、「博士の研究」が1枚以上、「モンスターボール」が1枚のみ、たねポケが1枚のみとなる場合のみであり、その確率は13.92%です。さらに、その条件下で、「博士の研究」を先に使ったときに「博士の研究」によりたねポケを引く確率から、「モンスターボール」を先に使ったときに「モンスターボール」で同じたねポケが出てかつ「博士の研究」でたねポケが引けなくなった確率を引く必要があります。つまり、たねポケがダークライとギラティナの4枚しかないことによる「モンスターボール」の強さが、この差がわずかとなる直接的な原因であると考えられます。

2ターン目終了時における確率

それぞれの状況における確率は以下のようになりました。ただし、「博士の研究」を先に使う場合を考えます。

状況	ダークライのみ	ギラティナのみ	ダークライ + ギラティナ
1T目 終了時	15.84 %	15.84 %	68.32 %
2T目 ドロー後	13.37 %	13.37 %	73.26 %
2T目 博士後	12.20 %	12.20 %	75.60 %
2T目 モンボ1枚目後	9.97 %	9.97 %	80.07 %
2T目 モンボ2枚目後	9.95 %	9.95 %	80.10 %

先行のとき、エネルギーを貼れるのは2ターン目からなので、1ターン目終了時にダークライを引けていなくても、2ターン目終了時までにダークライを引けばよいです。そのときの確率は、15.84 - 9.95 = 5.89%です。つまり、ダークライとギラティナの両方の特性が発動可能な理想的な盤面となる確率は、後攻のとき68.32%、先行のとき68.32 + 5.89 = 74.21%となります。

まとめ

確率分布の全探索シミュレーションにより、「博士の研究」を先に使う場合、それぞれの状況における確率は以下のようになりました。

状況	ダークライのみ	ギラティナのみ	ダークライ + ギラティナ
初期手札	41.18 %	41.18 %	17.65 %
1T目 終了時	15.84 %	15.84 %	68.32 %
2T目 終了時	9.95 %	9.95 %	80.10 %

この表から、ダークライとギラティナの両方の特性が発動可能な理想的な盤面となる確率は、後攻のとき68.32%、先行のとき74.21%と計算できます。

今回紹介した確率は、あくまでバトル開始時を基準とした確率です。実際の対戦では、ハンデスを警戒して「博士の研究」を温存したり、2ターン目にダークライを引く確率を少しでも上げるため1ターン目に「モンスターボール」を使わなかったりと、状況やプレイスタイルによって展開は無限に分岐していきます。また、ある行動を選んだ時点で、その後の確率はその行動を前提とした条件付きの確率へと更新され、その確率は、開始時に計算した確率とは別の値に変わっていきます。

---

使用したプログラム

今回作成したシミュレーターのコード全文です。

コード全文をコピーしてAIに「○○のデッキで、△△の条件における□□の確率を求めてください。」と伝えると、AIが計算結果を返してくれます！ぜひ試してください！

【プロンプト例】
以下のコードを用いて、種ポケをスイクン2枚、ケロマツ2枚、ギラティナ1枚、オドリドリ1枚の計6枚、博士の研究を2枚、モンスターボールを2枚とするとき、1ターン目終了までにギラティナを引ける確率を求めてください。
（ここにコードをペースト）

import itertools
from collections import defaultdict, Counter
from math import comb

# ===== パラメータ =====
total_cards = 20
hand_size = 5

# ===== ユーティリティ =====
def is_seed(card_id):
    return "Seed" in card_id

# ========== 初期手札 ==========
def build_initial_hand(ids):
    # デッキから初期手札を引く組み合わせの総数
    C = comb(total_cards, hand_size)
    out = defaultdict(float)
    ALL = range(total_cards)

    # 全ての初期手札の組み合わせを列挙
    for combh in itertools.combinations(ALL, hand_size):
        # 現在の組み合わせにおける手札と山札を生成
        hand = [ids[i] for i in combh]
        rest = [ids[i] for i in ALL if i not in combh]
        w0 = 1.0 / C

        if any(is_seed(i) for i in hand):
            # (1) 手札に種がある場合、その状態を保存
            # 状態を一意に識別するため、手札と山札をソートしてタプルに変換
            out[(tuple(sorted(hand)), tuple(sorted(rest)))] += w0
        else:
            # (2) 手札に種が無い場合、山札中の種から等確率で1枚を手札へ
            # https://qiita.com/machapin/items/a4d3b09d1b369c123e85
            seeds_idx_in_rest = [i for i, v in enumerate(rest) if is_seed(v)]  # 山札の種の位置
            S = len(seeds_idx_in_rest)
            if S == 0:
                raise ValueError("手札にも山札にも種ポケがありません。")
            else:
                # 山札の種を一つ選ぶ (確率 1/S)
                for s_idx in seeds_idx_in_rest:
                    # 手札の戻すカードを一つ選ぶ (確率 1/hand_size)
                    for r_idx in range(len(hand)):
                        hand2 = hand.copy()
                        rest2 = rest.copy()
                        hand2[r_idx], rest2[s_idx] = rest2[s_idx], hand2[r_idx]
                        out[(tuple(sorted(hand2)), tuple(sorted(rest2)))] += w0 * (1.0 / S) * (1.0 / hand_size)

    print("初期手札 状態数:", len(out))
    return out

# ========== 通常ドロー ==========
def apply_draw(dist):
    out = defaultdict(float)
    # 現在の分布の各状態についてループ
    for (hand_key, rest_key), w in dist.items():
        hand = list(hand_key)
        rest = list(rest_key)
        N = len(rest)
        if N == 0:
            # 山札が0枚ならドローできず、状態は変化しない
            out[(tuple(sorted(hand)), tuple(sorted(rest)))] += w
        else:
            # 山札の各カードを引く確率は等しく 1/N
            for i in range(N):
                hand2 = hand.copy()
                rest2 = rest.copy()
                drawn = rest2.pop(i)  # i番目のカードを引く
                hand2.append(drawn)  # 手札に加える
                out[(tuple(sorted(hand2)), tuple(sorted(rest2)))] += w * (1.0 / N)

    print(f"ドロー後 状態数: {len(out)}")
    return out

# ========== モンスターボール（MD） ==========
def apply_monster_ball(dist):
    out = defaultdict(float)
    # 現在の分布の各状態についてループ
    for (hand_key, rest_key), w in dist.items():
        hand = list(hand_key)
        rest = list(rest_key)

        # 手札に MD があるか探す
        mb_idx = next((i for i, v in enumerate(hand) if v == "MD"), None)
        # MDがない場合、状態は変化しない
        if mb_idx is None:
            out[(tuple(sorted(hand)), tuple(sorted(rest)))] += w
            continue
        
        # MDを1枚消費した手札を作成
        hand_wo_mb = hand.copy()
        hand_wo_mb.pop(mb_idx)

        # 山札にある種の位置をリストアップ
        seed_idx = [i for i, v in enumerate(rest) if is_seed(v)]
        N = len(seed_idx)
        if N == 0:
            # 山札に種が無ければ、MDは消費されるだけ
            out[(tuple(sorted(hand_wo_mb)), tuple(sorted(rest)))] += w
        else:
            # 山札の種を等確率 (1/N) で手札に加える
            for i in seed_idx:
                hand2 = hand_wo_mb.copy()
                rest2 = rest.copy()
                chosen = rest2.pop(i)  # 選ばれた種を山札から除く
                hand2.append(chosen)  # 手札に加える
                out[(tuple(sorted(hand2)), tuple(sorted(rest2)))] += w * (1.0 / N)

    print("モンボ後 状態数:", len(out))
    return out

# ========== 博士（PR） ==========
def apply_professor(dist):
    out = defaultdict(float)
    # 現在の分布の各状態についてループ
    for (hand_key, rest_key), w in dist.items():
        hand = list(hand_key)
        rest = list(rest_key)

        # 手札に PR があるか探す
        pr_idx = next((i for i, v in enumerate(hand) if v == "PR"), None)
        # PRがない、または山札が0枚なら、状態は変化しない
        if pr_idx is None or len(rest) == 0:
            out[(tuple(sorted(hand)), tuple(sorted(rest)))] += w
            continue
        
        # PRを1枚消費した手札を作成
        hand_wo_pr = hand.copy()
        hand_wo_pr.pop(pr_idx)
        N = len(rest)

        if N == 1:
            # 山札が1枚しかない場合、その1枚だけを引く
            hand2 = hand_wo_pr.copy()
            rest2 = rest.copy()
            drawn = rest2.pop(0)
            hand2.append(drawn)
            out[(tuple(sorted(hand2)), tuple(sorted(rest2)))] += w
        else:
            # 山札から2枚引く組み合わせの総数
            C2 = comb(N, 2)
            # 全ての2枚ドローの組み合わせを列挙
            for a, b in itertools.combinations(range(N), 2):
                # インデックスがずれないように、大きい方のインデックスからpopする
                i1, i2 = (a, b) if a < b else (b, a)
                hand2 = hand_wo_pr.copy()
                rest2 = rest.copy()
                card2 = rest2.pop(i2)
                card1 = rest2.pop(i1)
                hand2.append(card1)
                hand2.append(card2)
                out[(tuple(sorted(hand2)), tuple(sorted(rest2)))] += w * (1.0 / C2)

    print("博士後   状態数:", len(out))
    return out

# ========== 確率の計算 ==========
def prob_target(dist, require=None):  # require = {カードID: 許容される枚数の集合のタプル}
    out = defaultdict(float)
    prob = 0.0
    # 確率分布の各状態についてループ
    for (hand, rest), w in dist.items():
        hc = Counter(hand)
        # 条件を満たすか
        if all(hc.get(cid, 0) in allowed for cid, allowed in require.items()):
            out[(hand, rest)] += w
            prob += w

    # ラベル生成
    conds = [f"{cid} ∈ {allowed}" for cid, allowed in require.items()]
    label = " and ".join(conds) if conds else "no filters"

    print(f"{label} の確率: {prob*100:.6f} %  状態数: {len(out)}")
    return out


# ========== メイン関数 ==========
def main():
    # --- デッキの構築 ---
    # 各カードの枚数を指定
    ids = ["Seed1"]*2 + ["Seed2"]*2 + ["PR"]*2 + ["MD"]*2
    # 残りのカードを "Other" で埋める
    remain = total_cards - len(ids)
    ids.extend(["Other"]*remain)
    print(f"デッキ: {ids}")
    """
    デッキ構成（20枚）
    - Seed1: ダークライ 2枚
    - Seed2: ギラティナ 2枚
    - PR: 博士の研究 2枚
    - MD: モンスターボール 2枚
    - Other: その他（種以外） 12枚
    """

    # --- ゲーム開始時 ---
    dist = build_initial_hand(ids)
    # 初期手札で確率を計算
    prob_target(dist, require={"Seed1":(1, 2), "Seed2":(0,)})    # ダークライのみの確率
    prob_target(dist, require={"Seed1":(1, 2), "Seed2":(1, 2)})  # ダークライとギラティナが揃う確率

    # --- 1ターン目のアクション ---
    print("\n--- 1T目 ---")
    dist = apply_draw(dist)          # ドロー
    dist = apply_professor(dist)     # 博士
    dist = apply_monster_ball(dist)  # モンボ1枚目
    dist = apply_monster_ball(dist)  # モンボ2枚目
    # 1ターン目終了時点での確率を計算
    prob_target(dist, require={"Seed1":(1, 2), "Seed2":(0,)})    # ダークライのみの確率
    prob_target(dist, require={"Seed1":(1, 2), "Seed2":(1, 2)})  # ダークライとギラティナが揃う確率

    # --- 2ターン目のアクション ---
    print("\n--- 2T目 ---")
    dist = apply_draw(dist)          # ドロー
    dist = apply_professor(dist)     # 博士
    dist = apply_monster_ball(dist)  # モンボ1枚目
    dist = apply_monster_ball(dist)  # モンボ2枚目
    # 2ターン目終了時点での確率を計算
    prob_target(dist, require={"Seed1":(1, 2), "Seed2":(0,)})    # ダークライのみの確率
    prob_target(dist, require={"Seed1":(1, 2), "Seed2":(1, 2)})  # ダークライとギラティナが揃う確率

if __name__ == "__main__":
    main()

実行環境

Python：3.10.12

おわりに

ここまで読んでいただきありがとうございました。
お気づきの点やご指摘などがございましたら、ぜひコメントで教えていただけると幸いです！

前回の記事