🔰 活性化関数とは
-
活性化関数（Activation Function）は、ニューラルネットワークにおいて、複雑なパターンを学習可能にするための関数。
-
活性化関数の主な役割は次の3つ：
- 非線形性の導入：線形結合だけでは表現できない複雑な関数を近似
- 勾配の制御：逆伝播時の勾配の大きさを調整
- 出力の正規化：適切な範囲に出力値を制限
-
E資格では主要な活性化関数の数式・特徴・用途を理解しておく必要がある。
✅ 主要な活性化関数
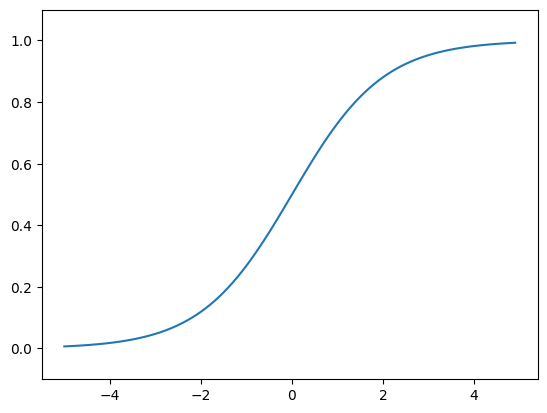
🔸 シグモイド関数（Sigmoid Function）
グラフと数式
- グラフ
- 活性化関数の式 $h(x)$・微分式 $h'(x)$
h(x) = \frac{1}{1 + e^{-x}}
h'(x) = h(x)(1 - h(x))
特徴
-
使用場面
- 二値分類の出力層（確率として解釈が可能）
- 従来のニューラルネットワークの隠れ層（最近ではあまり使われない）
-
利点
- 出力が0〜1の範囲で確率として解釈できる
- 計算が単純で実装しやすい
-
問題点
- 勾配消失問題：深い層で勾配が0に近づく
- 学習の収束が遅い：出力が0中心ではないため
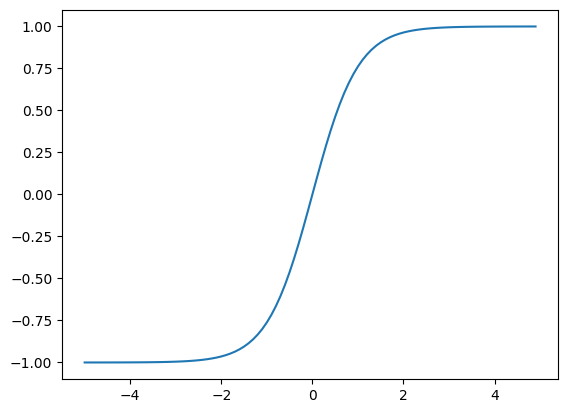
🔸 双曲線正接関数（Tanh Function）
グラフと数式
-
グラフ
-
活性化関数の式 $h(x)$・微分式 $h'(x)$
h(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = \frac{2}{1 + e^{-2x}} - 1
h'(x) = 1 - h^2(x)
特徴
-
使用場面
- LSTM・GRUのゲート機能
- 従来のニューラルネットワークの隠れ層
-
利点
- 0中心：シグモイドより学習が安定
-
問題点
- 勾配消失問題：シグモイド関数と同様に勾配が0に近づく
🔸 Softmax関数
グラフと数式
- グラフ
-
活性化関数の式 $h(x)$・微分式 $h'(x)$
nクラス分類の場合、入力ベクトル $\mathbf{x} = [x_1, x_2, ..., x_n]$ の各要素 $x_i$ に対して、次のように計算される：
h(x_i) = \frac{exp({x_i})}{\underset{j}{\sum} exp({x_j})}h'(x_i) = \sum_{j} \frac{\partial h(x_i)}{\partial x_j} \\\begin{align} \frac{\partial h(x_i)}{\partial x_j} &= h(x_i) \left( \delta_{ij} - h(x_j) \right) \\ &= \begin{cases} h(x_i) - h(x_i)^2 & (i = j) \\ -h(x_i)h(x_j) & (i \neq j) \end{cases} \end{align}- $\delta_{ij}$：クロネッカーのデルタといい、$i=j$ のとき $1$、それ以外のとき $0$ となる。
特徴
-
使用場面
- 多クラス分類の出力層では必須
- Attention機構
-
利点
- 多クラス分類に特化： 各出力値は0〜1の範囲で、全体の合計が1になるため、各値を「そのクラスである確率」として解釈できる（確率分布として扱える）
- ソフトマックス関数は入力ベクトルの要素間の差のみに依存するため、入力のスケールに対して不変である
- 入力の各要素に同じスカラー値を加えても、出力が変わらないという性質があり、$h(x) = h(x - \underset{i}{\max} x_i)$ で置き換えることができるため、結果として最大でも $exp(0) = 1$ となりオーバーフローの問題を回避できる。
-
問題点
- 計算コスト：出力の数が多い場合、計算が重くなる
- 勾配消失問題：入力値が大きいと勾配が0に近づく
🔸 恒等関数
グラフと数式
-
グラフ
-
活性化関数の式 $h(x)$・微分式 $h'(x)$
h(x) = x
h'(x) = 1
特徴
-
使用場面
- 回帰問題の出力層
- 特徴量の変換が不要な場合
-
利点
- 計算が高速：単純な関数で計算コストが低い
- 線形性：入力をそのまま出力するため、特に変換が不要な場合に有効
-
問題点
- 特徴量の変換が不要な場合には不向き
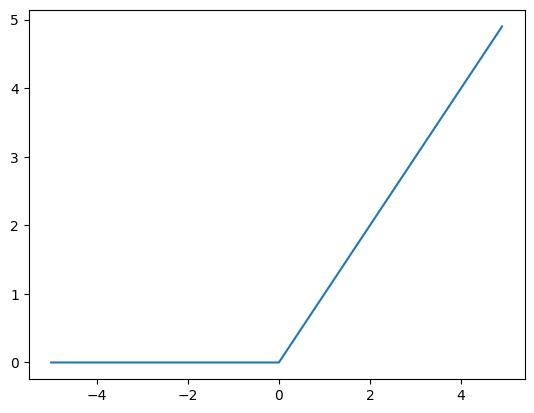
🔸 ReLU関数（Rectified Linear Unit）
グラフと数式
-
グラフ
-
活性化関数の式 $h(x)$・微分式 $h'(x)$
h(x) = \max(0, x) = \begin{cases}
x & \text{if } x > 0 \\
0 & \text{if } x \leq 0
\end{cases}
h'(x) = \begin{cases}
1 & \text{if } x > 0 \\
0 & \text{if } x \leq 0
\end{cases}
特徴
-
使用場面
- 深層ニューラルネットワークの隠れ層で最も一般的
- CNN（畳み込みニューラルネットワーク）
-
利点
- 勾配消失問題の軽減
- 計算が高速
- スパース性：一部のニューロンが0になりネットワーク全体の活性化が部分的になる現象。計算効率が向上し、不要な情報の伝播を抑制できる。
-
問題点
- Dying ReLU問題：入力が負の値の場合、勾配が0となるため、ニューロンが死ぬ
✅ 発展的な活性化関数
🔸 Leaky ReLU
グラフと数式
-
グラフ
-
活性化関数の式 $h(x)$・微分式 $h'(x)$
h(x) =
\begin{cases}
x & \text{if } x > 0 \\
\alpha x & \text{if } x \leq 0
\end{cases}
h'(x) =
\begin{cases}
1 & \text{if } x > 0 \\
\alpha & \text{if } x \leq 0
\end{cases}
ただし、$\alpha$ は正の定数で通常 $\alpha = 0.01$。
特徴
-
使用場面
- Dying ReLU問題を回避したい場合
- 一般的な深層学習モデル
-
利点
- ReLUの改良版：負の値でも小さな勾配を持つため、Dying ReLU問題を軽減
-
問題点
- 勾配が小さくなる可能性：負の値に対しても小さな勾配を持つが、0に近づくことがある
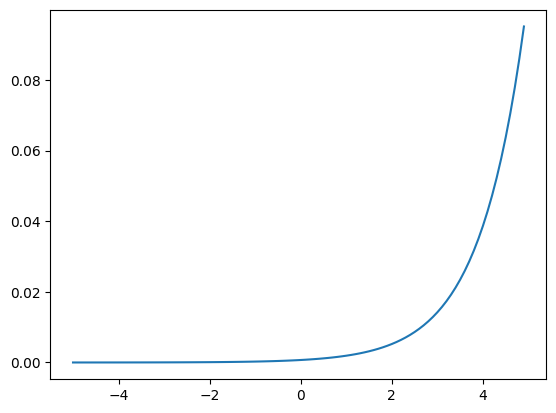
🔸 ELU（Exponential Linear Unit）
グラフと数式
-
グラフ
-
活性化関数の式 $h(x)$・微分式 $h'(x)$
h(x) = \begin{cases}
x & \text{if } x > 0 \\
\alpha(e^x - 1) & \text{if } x \leq 0
\end{cases}
h'(x) = \begin{cases}
1 & \text{if } x > 0 \\
\alpha e^x & \text{if } x \leq 0
\end{cases}
特徴
-
使用場面
- より安定した学習が必要な場合
-
利点
- ReLUの改良版：Leaky ReLUと同様、負の値でも小さな勾配を持つため、Dying ReLU問題を軽減
- 0中心に近い出力：負の値に対しても出力が0に近づくため、学習が安定しやすい
-
問題点
- 計算コストが高い：負の値に対しても指数関数を計算するため、計算コストが高くなる
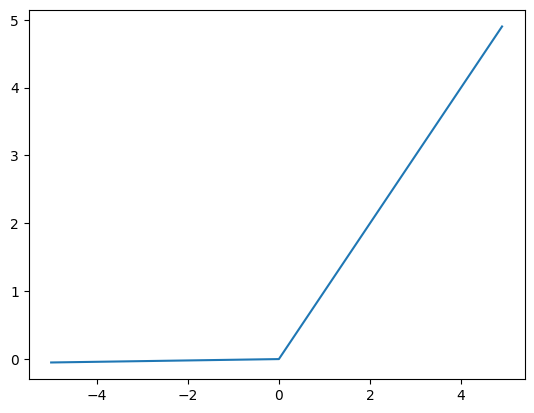
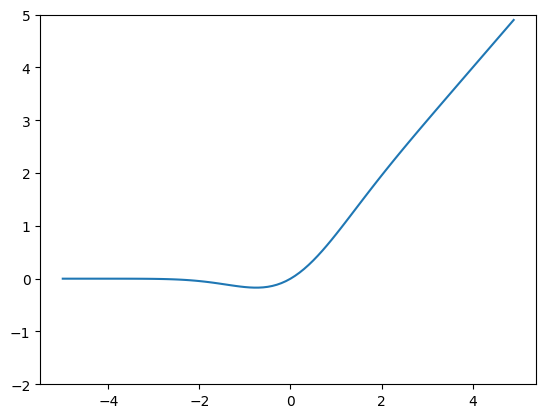
🔸 GELU
グラフと数式
-
グラフ
-
数式
h(x) = x \cdot \Phi(x)- $\Phi(x)$ ：標準正規分布の累積分布関数
特徴
-
使用場面
- Transformer系モデル（BERT、GPT） などで標準的に使用
- 高性能な自然言語処理や画像認識タスクにおけるデフォルトの活性化関数
-
利点
- ReLUとシグモイドの「いいとこ取り」
- 入力の値に応じてスムーズに非線形変換されるため、学習の安定性が高い
- 滑らかなS字曲線で微分可能かつ非線形性を保持
-
問題点
- 計算が複雑：近似式を用いても、ReLUよりは計算コストが高い
- 直感的にわかりづらい：ReLUのような「0かx」の単純な構造ではない
☝️ まとめ
それぞれの活性化関数の数式と微分
| 活性化関数 | 数式 | 微分 |
|---|---|---|
| シグモイド | $h(x) = \frac{1}{1 + e^{-x}}$ | $h'(x) = h(x)(1 - h(x))$ |
| 双曲線正接 | $h(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$ | $h'(x) = 1 - h^2(x)$ |
| Softmax | $h(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{K} e^{x_j}}$ | $h'(x) = h(x)(1 - h(x))$ |
| 恒等関数 | $h(x) = x$ | $h'(x) = 1$ |
| ReLU | $h(x) = \max(0, x) = \begin{cases} x & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases}$ | $h'(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases}$ |
| Leaky ReLU | $h(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases}$ | $h'(x) = \begin{cases} 1 & \text{if } x > 0 \\ \alpha & \text{if } x \leq 0 \end{cases}$ |
| ELU | $h(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha(e^x - 1) & \text{if } x \leq 0 \end{cases}$ | $h'(x) = \begin{cases} 1 & \text{if } x > 0 \\ \alpha e^x & \text{if } x \leq 0 \end{cases}$ |
それぞれの活性化関数の特徴
| 活性化関数 | 利点 | 問題点 |
|---|---|---|
| シグモイド | 出力が0〜1の範囲で解釈しやすい | 勾配消失問題 |
| 双曲線正接 | 0中心で学習が安定しやすい | 勾配消失問題 |
| Softmax | 多クラス分類に特化 | 計算コストが高い |
| 恒等関数 | 線形性があり解釈が容易 | 特徴量の変換が必要な場合に不向き |
| ReLU | 計算が高速で勾配消失問題を軽減 | Dying ReLU問題 |
| Leaky ReLU | Dying ReLU問題を回避 | 勾配が小さくなる可能性 |
| ELU | 学習が安定しやすい | 計算コストが高い |
活性化関数の選択指針
| 用途 | 推奨活性化関数 | 理由 |
|---|---|---|
| 二値分類出力 | Sigmoid | 確率として解釈可能 |
| 多クラス分類出力 | Softmax | 確率分布として解釈可能 |
| 回帰出力 | 恒等関数 | 出力値をそのまま実数として解釈可能 |
| 隠れ層 | ReLU | 計算効率、勾配消失問題の軽減 |
| LSTM/GRUゲート | Sigmoid/Tanh | ゲート機能に適した出力範囲 |
🎯 よく出題される内容
- ReLUとSigmoidの数式と特徴の比較
- Softmaxの数式と多クラス分類での役割
- 勾配消失問題と活性化関数の関係
- 各活性化関数の使用場面と選択理由