量子のQの字も知らない人間が3量子ビットでのGHZ状態を計算してみた
続編です
紛らわしくなりそうなのでタイトル変えました。(依然、Qの字も知らないです😭)
行列計算にチャレンジ
線形代数は学部1年目以来なので、下手すると高校生より計算できません。
とはいえ計算が楽になるならと、これを機にチャレンジです。
3量子ビットGHZ状態 (おさらい)
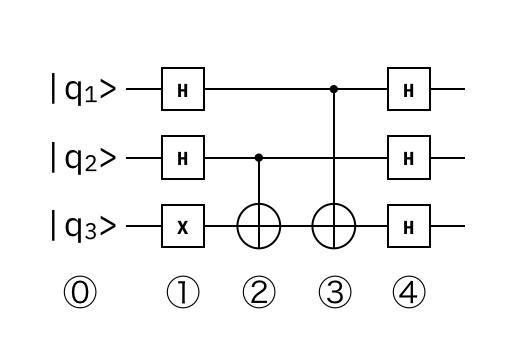
以下の図が、3量子ビットにおけるGHZ状態をつくりだす回路になります。
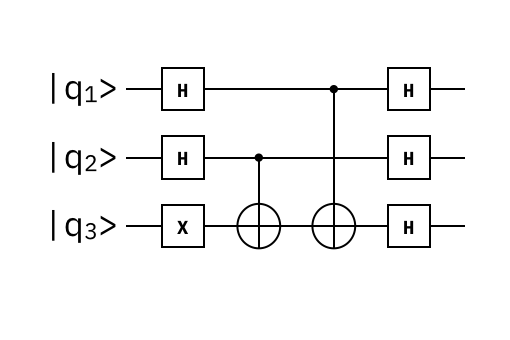
計算の番号付
各フェーズにおける行列計算
$CNOT_{c,t}$ で $c$量子ビット目が$\left|1\right>$のときに$t$量子ビット目を反転させます。
\begin{align}
&⓪ \quad q_{1} \otimes q_{2} \otimes q_{3} \\
&① \quad H \otimes H \otimes X \\
&② \quad CNOT_{2,3} \\
&③ \quad CNOT_{1,3} \\
&④ \quad H \otimes H \otimes H
\end{align}
ゲート毎の行列式
このとき、各ゲートの行列式は以下の通りです。
\begin{align}
H =
\frac{1}{\sqrt{2}}
\left[
\begin{array}{r}
1 & 1 \\
1 & -1 \\
\end{array}
\right] &, \quad
X =
\left[
\begin{array}{r}
0 & 1 \\
1 & 0 \\
\end{array}
\right] \\ \\
CNOT_{2,3} = I \otimes CNOT
=
\left[
\begin{array}{r}
1 & 0 \\
0 & 1 \\
\end{array}
\right]
\left[
\begin{array}{r}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0 \\
\end{array}
\right]
&=
\left[
\begin{array}{r}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\
\end{array}
\right], \\ \\
CNOT_{1,3}
&=
\left[
\begin{array}{r}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\
\end{array}
\right] \\
\end{align}
$CNOT_{1,3}$は気合で書いてみました、多分これであってるはず…
これを全てつなげて$GHZ_{3}$としましょう
GHZ_{3} = \bigl( H \otimes H \otimes H \bigr) \bullet CNOT_{1,3} \bullet CNOT_{2,3} \bullet \bigl( H \otimes H \otimes X \bigr) \bullet \bigl( q_{1} \otimes q_{2} \otimes q_{3} \bigr)
いざ計算
さすがに手計算だと死にそうなので、無難にNumpy使っていきたいと思います…
|000>でGHZ
# !/usr/bin/python
# -*- Coding: utf-8 -*-
import numpy as np
# calcs:行列積とテンソル積を行う高階関数
def calcs(func, *datas) :
if len(datas) != 1 :
return func(datas[0], calcs(func, *datas[1:]))
else :
return datas[0]
# 三項以上のテンソル積を求める関数
def krons(*datas) : return calcs(np.kron, *datas)
# 三項以上の行列積を求める関数
def prods(*datas) : return calcs(np.dot, *datas)
q1 = np.array([1,0])
q2 = np.array([1,0])
q3 = np.array([1,0])
H = 1 / np.sqrt(2) * np.array([[1,1],[1,-1]])
X = np.array([[0,1],[1,0]])
CNOT23 = np.array([ [1,0,0,0,0,0,0,0],
[0,1,0,0,0,0,0,0],
[0,0,0,1,0,0,0,0],
[0,0,1,0,0,0,0,0],
[0,0,0,0,1,0,0,0],
[0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1],
[0,0,0,0,0,0,1,0]])
CNOT13 = np.array([ [1,0,0,0,0,0,0,0],
[0,1,0,0,0,0,0,0],
[0,0,1,0,0,0,0,0],
[0,0,0,1,0,0,0,0],
[0,0,0,0,0,1,0,0],
[0,0,0,0,1,0,0,0],
[0,0,0,0,0,0,0,1],
[0,0,0,0,0,0,1,0]])
GHZ3 = prods(krons(H, H, H), CNOT13, CNOT23, krons(H, H, X), krons(q1, q2, q3))
print(GHZ3)
出力結果
[ 0.70710678 0. 0. 0. 0. 0.
0. -0.70710678]
もつれた!
終わりに
PythonライブラリのNumpyを使って、行列式で3量子ビットのGHZ計算できました。
ひたすらGHZをやってますが、ここが量子ビットの本質ではないことも重々承知なので、今後も勉強を続けて量子エンジニア目指していきます!