ニッセイ情報テクノロジー　PS事業推進室 Advent Calendar 2025

量子アニーリング入門：jaxで量子アニーリングを書いてGPU上で動かしてみた

Last updated at 2025-12-09Posted at 2025-12-09

この記事はニッセイ情報テクノロジーPS事業推進室アドベントカレンダー2025の10日目の記事になります。

導入

社内でも「量子コンピューティング」という言葉を耳にする機会が増えてきました。話についていくためにその概念くらいはおさえておきたいなと思いアドベントカレンダーを機に簡単に整理、実装してみようと思います。
量子コンピューティングの応用は多岐に渡りますが、今回は組合せ最適化と相性が良いとされる量子アニーリングに焦点を当て、そのシミュレーション実装に必要な事項をかいつまんで整理しつつ、古典的な手法（焼きなまし法など）とのちがいも実験を通じて雰囲気をつかんでみます。

構成

記事は下記構成です。

焼きなまし法(SA)と疑似量子アニーリング(SQA)の概観
「量子らしさ」が活きやすいToy Modelを使った挙動比較

焼きなまし法(SA)と疑似量子アニーリング(SQA)の概観

長さ$n$のビット列$x_i \in \lbrace 0,1 \rbrace$、または線形変換$s_i=2x_i-1$でIsing変数$s_i \in \lbrace -1 ,1 \rbrace$のスピン列に移して

E(s)=-\sum_ih_is_i-\sum_{i<j} J_{ij} s_i s_j

というエネルギー関数を最小化する形で問題、すなわちこのエネルギーをなるべく小さくするスピン配置$s$を見つける問題を見ていきます。

焼きなまし法（SA）によるエネルギー最小化

エネルギー最小化を愚直に行う方法はスピンの配置$s$($2^N$通り)の全探索で一番エネルギーの低い解を見つけるというものですが、$N$が大きくなると総当りは現実ではありません。
そこで完全でなくともより良い解を探索する方法の一つとして焼きなまし法がよく利用されます。

ここでは代表的な焼きなまし法として

ボルツマン分布を目標分布としたメトロポリス-ヘイスティング型のマルコフ連鎖モンテカルロ法（MCMC）を温度を徐々に下げながら実行する

という最適化アルゴリズムをSQAの比較対象として考えます。すなわち状態$s$に対してエネルギー関数$E(s)$とボルツマン分布$\pi(s) \propto \exp (-E(s)/T)$が与えられているとき、次のように動きます。

初期化
1. 初期状態 $s \leftarrow s_0$ をランダムに生成する
2. $E \leftarrow E(s)$ を計算する
3. $s_{\mathrm{best}} \leftarrow s,\quad E_{\mathrm{best}} \leftarrow E$
4. 温度を $T \leftarrow T_0$ とする
温度ループ
while T > T_min かつ規定ステップ数に達していない間:
1. MCMCステップ（その温度での反復）
  for i = 1, 2, ..., N_iter:
  1. 現在の状態を (s) とする
  2. 提案分布 $q(s \rightarrow s')$ に従って候補状態 $s'$ をサンプリングする
  3. エネルギー差$\Delta E \leftarrow E(s') - E(s)$を計算する
  4. 遷移の受理確率
    A(s \rightarrow s') = \min\left(1, \exp(-\Delta E / T)\frac{q(s' \rightarrow s)}{q(s \rightarrow s')}\right)
    を計算する
    ※提案分布が対称 $q(s \rightarrow s') = q(s' \rightarrow s)$ のときは
    A(s \rightarrow s') = \min\left(1, \exp(-\Delta E / T)\right)
    に簡略化される
  5. 一様乱数 $u \sim \mathrm{Uniform}(0,1)$ を生成する
  6. もし $u \le A(s \rightarrow s')$ なら:
    - 状態とエネルギーを更新$s \leftarrow s',\quad E \leftarrow E(s')$
  7. もし $E < E_{\mathrm{best}}$ なら:
    - 最良解を更新$s_{\mathrm{best}} \leftarrow s,\quad E_{\mathrm{best}} \leftarrow E$
2. 温度の更新
  - 冷却スケジュールに従って温度を更新$T \leftarrow \text{UpdateTemperature}(T)$
終了
- ループを抜けた時点での $s_{\mathrm{best}}$ を解として返す

高温では解が悪化する$\Delta E>0$ の遷移も受理されやすく，多様な状態を探索できます。温度を下げるにつれて悪化する遷移が受理されにくくなり，最終的には低エネルギーの谷に留まることを狙う，というのが焼きなまし法の直感的な振る舞いです。
ただ途中で非常に高いエネルギー障壁を超える必要がある問題設定では、確率的にその障壁をこえることができず良い解に至らないケースもあり、これが焼きなまし法を適用するときの課題の一つとなります。

疑似量子アニーリング(SQA)によるエネルギー最小化

量子アニーリングは量子揺らぎを利用して最適化問題の正解を見つける汎用アルゴリズムです。ここでは量子力学の現象が計算できるアルゴリズムにどのように変換されるのか、その雰囲気を簡単に追ってみます。¹

今回の問題設定のように状態としてスピンをとり，古典Isingモデルのエネルギー

E_{class}(s)=-\sum_ih_is_i-\sum_{i<j} J_{ij} s_i s_j

を量子アニーリングでQUBO を表す場合，これを問題ハミルトニアンとして量子化します。

ここで少しだけ量子ビットの表現に切り替えます。
古典ビット0,1に対応する1ビットを
\ket{\uparrow}=\begin{pmatrix}1\\0\end{pmatrix},\ket{\downarrow}=\begin{pmatrix}0\\1\end{pmatrix}
と書きます。また１ビットの均等な重ね合わせ状態として
\ket{+} = \frac{\ket{\uparrow}+\ket{\downarrow}}{\sqrt{2}}
という状態を考えます。この$\ket{+}$は測定すると、0,1がそれぞれ50%の確率で出てくるという「１ビットの均等な重ね合わせ状態」とみなせます。Nビットすべてを$\ket{+}$にした状態
\ket{\Phi(0)}=\frac{1}{2^{N/2}} \prod_i(\ket{\uparrow}_i+\ket{\downarrow}_i)
はすべてのビット列の一様重ね合わせになっていて、量子アニーリングではこれを「自明だが都合のいい初期状態」として扱います。

QUBOのエネルギー関数はz方向スピン演算子$\sigma^z_i$を使って

H_0=-\sum_i h_i \sigma^z_i-\sum_{i<j} J_{ij} \sigma^z_i \sigma^z_j

として量子化できます。目的はこのハミルトニアンの基底状態（最低のエネルギーを得られる状態）を見つけることです。
ここに、すべてのスピンが$\ket{+}$になる状態$\ket{\Phi(0)}$を基底状態に持つ横磁場ハミルトニアン

H_1 = - \sum_i\sigma^x_i

を足し合わせ

H(t) = A(t)H_0 + \Gamma(t)H_1

のようなハミルトニアンを考えます。ここで

第1項: 問題のハミルトニアン(古典QUBOに対応)
第2項: 横磁場(量子揺らぎ)

です。「時間とともに係数$A(t), \Gamma(t)$を変化させていきます。このように最初に$H_1$の基底状態$\ket{\Phi(0)}$からはじめて十分ゆっくり$H_0$へ変形すれば、系はその瞬間の基底状態を連続的にたどって、最終的に目的のハミルトニアンの基底状態（=QUBOの最適解）に到達してくれるはず。」というのが基底状態を効率的に求める断熱量子計算のアイデアです。

しかしこの時間依存の量子ダイナミクスをそのまま古典計算機で解くのは困難です。そこで SQA では、時間発展ではなく熱平衡分布に注目し、横磁場付き Isingモデルを「空間 × トロッター方向」に拡張した以下のような分配関数、ボルツマン分布を持つ古典 Isingモデルに近似します。

Z(\Gamma, T)
  \simeq \sum_{\boldsymbol\sigma}
          \exp\bigl(-E_{\mathrm{SQA}}(\boldsymbol\sigma; \Gamma)/T\bigr),

\pi(\boldsymbol\sigma; \Gamma)
  \propto \exp\bigl(-E_{\mathrm{SQA}}(\boldsymbol\sigma; \Gamma)/T\bigr)

この近似のもとでスピン配位$\boldsymbol\sigma$に対して古典エネルギーは下記のようにかけます。

E_{\mathrm{SQA}}(\boldsymbol\sigma; \Gamma)
= \sum_{k=1}^{M}
  \Bigl[
    - \sum_{i<j} J_{ij}\, s_i^{(k)} s_j^{(k)}
    - \sum_i h_i\, s_i^{(k)}
  \Bigr]
  - J_\perp(\Gamma)\sum_{i,k} s_i^{(k)} s_i^{(k+1)}

ここで

\boldsymbol\sigma
= (s_i^{(k)})_{i=1,\dots,N;\,k=1,\dots,M}
\in \{-1,+1\}^{N\times M},

J_\perp(\Gamma)
  = -\frac{1}{2\beta}\,\ln\!\bigl[\tanh(\beta \Gamma / M)\bigr],\qquad
s_i^{(k)} \in \{-1,+1\},

であり、トロッター方向には周期境界条件$s_i^{(M+1)} \equiv s_i^{(1)}$を設けます(平衡状態)。
つまり、元の Ising エネルギー

E_{\mathrm{class}}(s)
 = -\sum_i h_i s_i - \sum_{i<j} J_{ij} s_i s_j

をトロッター方向にM層コピーし、横磁場 $\Gamma$ に対応する縦方向結合 $J_\perp(\Gamma)$ で各層のスピンを結びつけた、いわゆる「量子揺らぎの効果を織り込んだ」拡張 Ising モデルになっています。

このようにして得たボルツマン分布をMCMCでサンプリングすることで、古典計算機上で量子アニーリングをシミュレートすることができます。このときアルゴリズムは次のような動きになります。

初期化
1. 逆温度（または温度）を設定する: $ T \leftarrow T_0 \quad (\beta = 1/T_0)$
2. 横磁場を強い値に設定する: $ \Gamma \leftarrow \Gamma_{\mathrm{init}}$
3. 初期スピン配位 $\boldsymbol\sigma = (s_i^{(k)})$ をランダムに生成する
  （全てのサイト $(i,k)$ について $s_i^{(k)} \in \lbrace-1,+1\rbrace$ を一様ランダムに選ぶ）
4. 有効古典エネルギーを計算する: $
  E_{\mathrm{SQA}} \leftarrow E_{\mathrm{SQA}}(\boldsymbol\sigma; \Gamma)
  $
5. トロッター方向を潰して元のスピングラスの候補解 $s$ を作る
  （例：多数決）
```
s_i = \mathrm{sign}\left(\sum_{k=1}^M s_i^{(k)}\right)
```
6. 元の Ising / QUBO のエネルギー $E_{\mathrm{class}}(s)$ を計算し，
```
s_{\mathrm{best}} \leftarrow s,\quad
E_{\mathrm{best}} \leftarrow E_{\mathrm{class}}(s)
```
  として最良解を初期化する。
アニーリング（横磁場）ループ
while Γ > Γ_final かつ規定ステップ数に達していない間:
1. MCMC ステップ（その Γ での反復）
  for i = 1, 2, ..., N_iter:
  1. 現在のスピン配位を $\boldsymbol\sigma$ とする
  2. 近傍構造と提案分布 $q(\boldsymbol\sigma \rightarrow \boldsymbol\sigma')$ に従い，
    候補状態 $\boldsymbol\sigma'$ をサンプリングする
    例：
    - 単一スピン反転：ランダムな $(i,k)$ を選び $s_i^{(k)} \rightarrow -s_i^{(k)}$ とする
  3. 有効古典エネルギー差
    \Delta E \leftarrow E_{\mathrm{SQA}}(\boldsymbol\sigma'; \Gamma) - E_{\mathrm{SQA}}(\boldsymbol\sigma; \Gamma)
    を計算する。
  4. 遷移の受理確率
    A(\boldsymbol\sigma \rightarrow \boldsymbol\sigma') = \min\left( 1,\, \exp(-\Delta E/T)\, \frac{q(\boldsymbol\sigma' \rightarrow \boldsymbol\sigma)} {q(\boldsymbol\sigma \rightarrow \boldsymbol\sigma')} \right)
    を計算する。
    ※提案分布が対称 $q(\boldsymbol\sigma \rightarrow \boldsymbol\sigma')
    = q(\boldsymbol\sigma' \rightarrow \boldsymbol\sigma)$ のときは
    A(\boldsymbol\sigma \rightarrow \boldsymbol\sigma') = \min\left(1, \exp(-\Delta E/T)\right)
    に簡略化される。
  5. 一様乱数 $u \sim \mathrm{Uniform}(0,1)$ を生成する
  6. もし $u \le A(\boldsymbol\sigma \rightarrow \boldsymbol\sigma')$ なら:
    - 配位とエネルギーを更新する
      \boldsymbol\sigma \leftarrow \boldsymbol\sigma',\quad E_{\mathrm{SQA}} \leftarrow E_{\mathrm{SQA}}(\boldsymbol\sigma'; \Gamma)
  7. 更新後の $\boldsymbol\sigma$ から，元の問題のスピン列 $s$ を再構成する
    （例：多数決）
    s_i = \mathrm{sign}\left(\sum_{k=1}^M s_i^{(k)}\right)
  8. 元のエネルギー $E_{\mathrm{class}}(s)$ を計算し，
    もし $E_{\mathrm{class}}(s) < E_{\mathrm{best}}$ なら:
    - 最良解を更新する
      s_{\mathrm{best}} \leftarrow s,\quad E_{\mathrm{best}} \leftarrow E_{\mathrm{class}}(s)
2. 横磁場の更新
  - アニーリングスケジュールに従って横磁場を弱める
    \Gamma \leftarrow \text{UpdateGamma}(\Gamma)
  - 新しい $\Gamma$ に対して結合定数
    J_\perp(\Gamma) = -\frac{1}{2\beta}\,\ln\!\bigl[\tanh(\beta \Gamma / M)\bigr]
    を再計算し，それに応じて
    E_{\mathrm{SQA}}(\boldsymbol\sigma; \Gamma)
    のパラメータも更新する。
終了
- ループを抜けた時点での $s_{\mathrm{best}}$ を，
  スピングラス（元の QUBO/Ising）の近似解として採用する。

SA・SQAさっくり比較表

ここまで実装に必要な要素をながめてきたので、表で比較をしてみます。

項目	焼きなまし法 (SA)	疑似量子アニーリング (SQA)
エネルギー関数	$E_{\mathrm{class}}(s)$	$E_{\mathrm{SQA}}(\boldsymbol\sigma; \Gamma)$
状態変数	スピン列 $s = (s_i)_{i=1}^N,\ s_i \in \lbrace-1,+1\rbrace$	トロッター方向も含むスピン配位 $\boldsymbol\sigma = (s_i^{(k)}) \in \lbrace-1,+1\rbrace^{N\times M}$
分布	$\pi(s) \propto \exp(-E_{\mathrm{class}}(s)/T)$	$\pi(\boldsymbol\sigma; \Gamma) \propto \exp(-E_{\mathrm{SQA}}(\boldsymbol\sigma; \Gamma)/T)$
近傍の例	単一スピン反転、2-opt など	単一スピン反転、ワールドライン更新、クラスタ更新など
受理確率	$A(s \to s') = \min\bigl(1, \exp(-\Delta E/T)\bigr)$	$A(\boldsymbol\sigma \to \boldsymbol\sigma') = \min\bigl(1, \exp(-\Delta E_{\mathrm{SQA}}/T)\bigr)$（対称提案分布の場合）
アニーリングパラメータ	温度 $T$（高温 $\to$ 低温）	横磁場の強さ $\Gamma$（大きい $\Gamma \to$ 小さい $\Gamma$）＋必要なら温度スケジュール
探索メカニズムの直感	熱ゆらぎでエネルギー障壁を飛び越えつつ、温度を下げて谷に落ち着く	量子揺らぎ（トロッター方向の結合）を$\Gamma$で束ねて古典問題に収束
古典 Ising との対応	そのまま	各トロッター層の多数決などで $\boldsymbol\sigma \mapsto s$ に射影して評価
計算コスト	1 本のスピン列を更新	トロッター数M本のスピン列を同時に持つため、メモリ・計算量ともにおよそM 倍

「量子らしさ」が活きやすいToy Modelを使った挙動比較

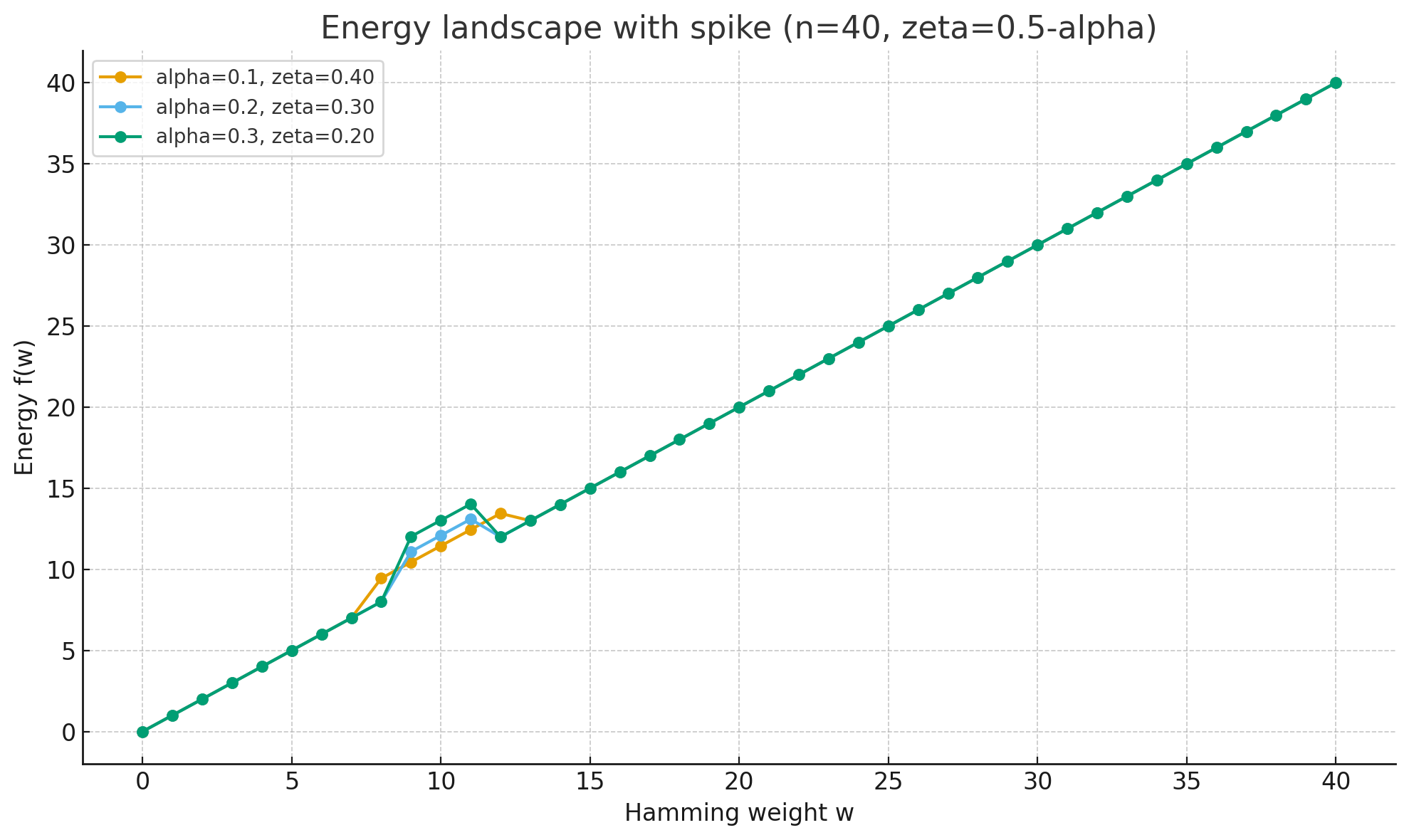
以上の比較をもとに、量子らしさが効きやすいスパイク付きHamming関数をエネルギーとした最適化をしてみます。²

モデルの概要

長さ (n) のビット列 $ x \in \lbrace 0,1 \rbrace^n $ の Hamming 重み

w(x)=\sum_i x_i

に基づいてコストを定義します。

基礎となるコストは

E_{base}(x)=w(x),

つまり「1 の個数が少ないほど良い」という単調な地形です。

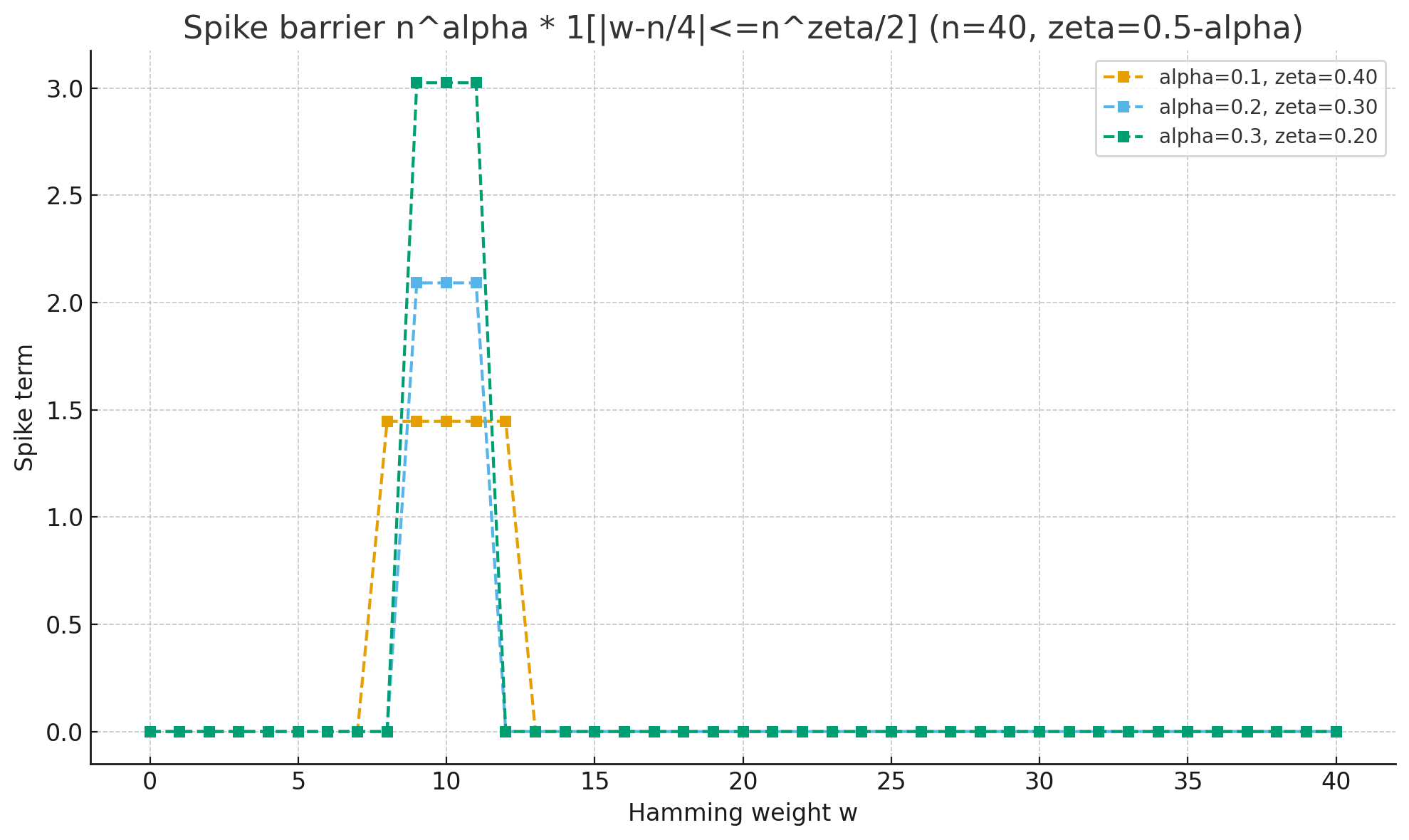
ここに「人工的なエネルギー障壁 (spike)」を加えます：

E(x) = w(x) + n^\alpha \cdot
  \mathbf{1}\Bigl(\bigl|w(x)-\tfrac{n}{4}\bigr|\le \tfrac{n^\zeta}{2}\Bigr)

spike の中心：(w \approx n/4)
spike の幅：(n^\zeta)
spike の高さ：(n^\alpha)

つまり 坂道の途中に、細くて高い障壁をわざと置いた地形 になります。

焼きなましの観点では、ランダムな初期状態ではだいたい$w(x)=n/2$`あたりから始まり、ビット反転によって$w(x)=0$側に近づいていくことが期待できますが、その途中で一時的にエネルギーが増加する領域を通らなければならない、というような問題設定になります。

SA/SQAの比較において何が嬉しいのか？

SA（焼きなまし）
単ビット反転で少しずつ移動するため、spike が高いと 壁の手前で詰まりやすい
SQA（疑似量子アニーリング）
トロッター方向の複数レイヤを束ねた更新により、壁を越えやすい（量子トンネル的） 挙動が期待できる

実験

MCMCを並列で効率的に実行するため、SA, SQAをjaxで実装して結果を比較してみます。
スパイクが高くなるよう$\alpha=0.4, \zeta=0.1$、500としてビット列の長さnを変えながら挙動を確認します。

実験結果

実験プログラム

import jax
import jax.numpy as jnp
from jax import random, lax
from functools import partial

jax.config.update("jax_enable_x64", True)

# =========================================
# Hamming spike cost
# =========================================

def cost_from_w(w, n, alpha=0.4, zeta=0.2):
    spike_center = n / 4.0
    spike_width  = n ** zeta
    spike_height = n ** alpha
    in_spike = jnp.abs(w - spike_center) <= (spike_width / 2.0)
    return w + spike_height * in_spike.astype(w.dtype)


def cost_from_spins(spins, alpha=0.4, zeta=0.2):
    """
    spins: (batch, n) in {-1,+1}
    """
    n = spins.shape[-1]
    w = 0.5 * (n + spins.sum(axis=-1, dtype=jnp.float64))
    return cost_from_w(w, n, alpha, zeta)


# =========================================
# SA
# =========================================

@partial(jax.jit, static_argnames=("n_spins", "batch_size", "n_steps"))
def run_sa(
    key,
    n_spins=64,
    batch_size=512,
    n_steps=5000,
    T_start=2.0,
    T_end=0.2,
    alpha=0.39,
    zeta=0.2,
):
    n = n_spins

    # 初期スピン (batch, n_spins) in {-1,+1}
    key, sub = random.split(key)
    spins = 2 * random.bernoulli(sub, 0.5, (batch_size, n_spins)) - 1
    spins = spins.astype(jnp.int8)

    # 初期エネルギー
    w = 0.5 * (n + spins.sum(axis=-1, dtype=jnp.float64))
    E = cost_from_w(w, n, alpha, zeta)

    best_E = E
    best_spins = spins

    T_sched = jnp.linspace(T_start, T_end, n_steps)
    batch_idx = jnp.arange(batch_size)

    def body(step, carry):
        spins, w, E, best_E, best_spins, key = carry
        key, k_idx, k_u = random.split(key, 3)

        T = T_sched[step]
        beta = 1.0 / T

        # 各バッチで 1 スピンを候補
        flip_idx = random.randint(k_idx, (batch_size,), 0, n_spins)
        s = spins[batch_idx, flip_idx].astype(jnp.int8)

        new_w = w - s.astype(jnp.float64)
        E_old = E
        E_new = cost_from_w(new_w, n, alpha, zeta)
        dE = E_new - E_old

        accept_prob = jnp.exp(-beta * dE)
        accept = (dE <= 0.0) | (random.uniform(k_u, (batch_size,)) < accept_prob)

        # 更新
        new_spins_val = jnp.where(accept, -s, s)
        spins_new = spins.at[batch_idx, flip_idx].set(new_spins_val)

        w_new = jnp.where(accept, new_w, w)
        E_new2 = jnp.where(accept, E_new, E_old)

        better = E_new2 < best_E
        best_E_new = jnp.where(better, E_new2, best_E)
        best_spins_new = jnp.where(better[:, None], spins_new, best_spins)

        return (spins_new, w_new, E_new2, best_E_new, best_spins_new, key)

    spins, w, E, best_E, best_spins, key = lax.fori_loop(
        0, n_steps, body, (spins, w, E, best_E, best_spins, key)
    )

    return best_E, best_spins


# =========================================
# SQA
# =========================================

@partial(
    jax.jit,
    static_argnames=(
        "n_spins",
        "batch_size",
        "n_trotter",
        "n_steps",
        "updates_per_step",
    ),
)
def run_sqa(
    key,
    n_spins=64,
    batch_size=512,
    beta=4.0,
    n_trotter=16,
    n_steps=5000,
    Gamma_start=2.0,
    Gamma_end=0.05,
    alpha=0.39,
    zeta=0.1,
    updates_per_step=1,
):
    """
    途中経過ログなしの高効率版 SQA。
    返り値:
      best_E:   (batch,)
      best_spins: (batch, n_spins)
    """
    M = n_trotter
    n = n_spins
    B = batch_size

    key, sub = random.split(key)
    # spins: (B, M, n) in {-1,+1}
    spins = 2 * random.bernoulli(sub, 0.5, (B, M, n)) - 1
    spins = spins.astype(jnp.int8)

    # w: (B, M)
    w = 0.5 * (n + spins.sum(axis=-1, dtype=jnp.float64))
    batch_idx = jnp.arange(B)

    def one_step(step, carry):
        spins, w, key = carry

        # Annealing schedule
        Gamma = Gamma_start + (Gamma_end - Gamma_start) * (
            step / (n_steps - 1)
        )
        x = beta * Gamma / M
        t = jnp.tanh(x)
        t = jnp.maximum(t, 1e-6)
        J_tau = 0.5 * jnp.log(1.0 / t)

        def inner_update(c, _):
            spins_i, w_i, key_i = c
            key_i, k_trot, k_spin, k_u = random.split(key_i, 4)

            k_idx = random.randint(k_trot, (B,), 0, M)
            i_idx = random.randint(k_spin, (B,), 0, n)

            s = spins_i[batch_idx, k_idx, i_idx].astype(jnp.int8)

            k_prev = (k_idx - 1) % M
            k_next = (k_idx + 1) % M
            s_prev = spins_i[batch_idx, k_prev, i_idx].astype(jnp.int8)
            s_next = spins_i[batch_idx, k_next, i_idx].astype(jnp.int8)

            w_old = w_i[batch_idx, k_idx]
            w_new = w_old - s.astype(jnp.float64)

            E_old_z = cost_from_w(w_old, n, alpha, zeta)
            E_new_z = cost_from_w(w_new, n, alpha, zeta)
            dE_z = (beta / M) * (E_new_z - E_old_z)

            dE_tau = 2.0 * J_tau * s.astype(jnp.float64) * (
                s_prev.astype(jnp.float64) + s_next.astype(jnp.float64)
            )

            dE = dE_z + dE_tau
            accept_prob = jnp.exp(-dE)
            accept = (dE <= 0.0) | (random.uniform(k_u, (B,)) < accept_prob)

            new_spin_val = jnp.where(accept, -s, s)
            spins_new = spins_i.at[batch_idx, k_idx, i_idx].set(new_spin_val)

            w_layer_new = jnp.where(accept, w_new, w_old)
            w_new_full = w_i.at[batch_idx, k_idx].set(w_layer_new)

            return (spins_new, w_new_full, key_i), None

        (spins, w, key), _ = lax.scan(
            inner_update, (spins, w, key), None, length=updates_per_step
        )
        return (spins, w, key)

    spins, w, key = lax.fori_loop(
        0, n_steps, one_step, (spins, w, key)
    )

    # バッチごとの best layer を選択
    def select_best(spins_b):
        # spins_b: (M, n)
        n_local = spins_b.shape[-1]
        w_b = 0.5 * (n_local + spins_b.sum(axis=-1, dtype=jnp.float64))  # (M,)
        E_b = cost_from_w(w_b, n_local, alpha, zeta)
        k_best = jnp.argmin(E_b)
        return E_b[k_best], spins_b[k_best]

    best_E, best_spins = jax.vmap(select_best)(spins)  # (B,), (B,n)
    return best_E, best_spins


# =========================================
# main
# =========================================

def main():
    key = random.PRNGKey(0)

    # 対象とする n
    n_list = [64, 128, 256, 512, 1024]
    sa_steps_list  = [100_000, 200_000, 400_000, 800_000, 1_600_000]
    sqa_steps_list = [100_000, 200_000, 400_000, 800_000, 1_600_000]
    batch_size = 512

    # Hamming spike
    alpha = 0.45
    zeta  = 0.05

    for n_spins, sa_steps, sqa_steps in zip(n_list, sa_steps_list, sqa_steps_list):
        print("=" * 50)
        print(f"n_spins = {n_spins}, alpha = {alpha}, zeta = {zeta}")
        print(f"SA  steps = {sa_steps}, SQA steps = {sqa_steps} (updates_per_step=1)")

        key, key_sa, key_sqa = random.split(key, 3)

        # --- SA ---
        best_E_sa, _ = run_sa(
            key_sa,
            n_spins=n_spins,
            batch_size=batch_size,
            n_steps=sa_steps,
            T_start=2.0,
            T_end=0.2,
            alpha=alpha,
            zeta=zeta,
        )
        sa_mean = float(best_E_sa.mean())
        sa_min = float(best_E_sa.min())
        print(f"[SA ] mean_best_E = {sa_mean:.6f}, min_best_E = {sa_min:.6f}")

        # --- SQA ---
        best_E_sqa, _ = run_sqa(
            key_sqa,
            n_spins=n_spins,
            batch_size=batch_size,
            beta=4.0,
            n_trotter=8,
            n_steps=sqa_steps,
            Gamma_start=2.0,
            Gamma_end=0.05,
            alpha=alpha,
            zeta=zeta,
            updates_per_step=1,  
        )
        sqa_mean = float(best_E_sqa.mean())
        sqa_min = float(best_E_sqa.min())
        print(f"[SQA] mean_best_E = {sqa_mean:.6f}, min_best_E = {sqa_min:.6f}")


if __name__ == "__main__":
    main()

スピン数を変えながら実験した結果をテーブルにまとめます。$\Delta E$ は spike の高さの目安です。

スピン数が増えてスパイクが高くなるほどSQAのほうが良い結果を得られる傾向が見られました。
min(全バッチでの最良の結果)からn=512以降でSAは初期値から改善できていない一方でSQAでは改善が見られています。
またmean_best(バッチ内での最良値の平均)の比較からSAでは障壁を飛び越えられていないバッチが多い一方で、SQAは全体的に障壁を飛び越えられているものが多いことが読み取れます。
ただn=1024の結果から障壁が高すぎるとSQAといえど良い結果にたどり着きにくいことも見えています。

n_spins	steps	SA mean_best	SA min	SQA mean_best	SQA min	ΔE	p = exp(-ΔE) @ T=1
64	1x10^5	4.1	0.0	1.6	0.0	7.50	5.5e-04
128	2x10^5	26.4	0.0	3.7	0.0	9.87	5.2e-05
256	4x10^5	64.5	0.0	9.8	2.0	13.12	2.0e-06
512	8x10^5	129.0	129.0	104.5	25.0	17.56	2.4e-08
1024	16x10^5	257.0	257.0	254.5	233.0	23.63	5.5e-11

まとめ

SQAの実装に必要な理論を概観した後、高くて薄い障壁を持つモデルに対してSA/SQAをJAXで実装することで、量子効果を模したシミュレーションが有効なケースがあることを確認できました。TSPやナーススケジュールなど現実によくあるケースではどのような振る舞いになるかは時間があればまた検証してみたいと思います。

参考資料

導出に関してはこちらが大変わかりやすかったです(https://qiita.com/ground0state/items/0f61c3efc7f12fd96d05) ↩
Simulated Quantum Annealing Can Be Exponentially Faster than Classical Simulated Annealing
(https://arxiv.org/abs/1601.03030) ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up