はじめに
Kuwaharaフィルタは画像処理フィルタの一種で、物体の輪郭を残したまま画像のノイズを除去することが可能です。また、少し前に写真を絵画っぽく変換できる画像処理フィルタとして話題になりました。
今回はこのKuwaharaフィルタの処理を、クライアントサイドのブラウザで実行可能なようにJavascriptで実装してみました。こちらのWebアプリで実際に処理を試すことが出来ます。
アルゴリズム
Kuwaharaフィルタのアルゴリズムの紹介です。(Wikipedia参照)
あるピクセルの輝度値$I(x,y)$を決めるにあたり、まずは周辺$2a+1 $の正方形を4つの領域に分割し$Q_i(x,y)$を定義します。
※$a$はフィルタ大きさ、$\times$はデカルト積を意味する
Q_i(x,y) =
\left\{
\begin{array}{ll}
[x,x+a] \times [y,y+a] & if \; i = 1 \\
[x-a,x] \times [y,y+a] & if \; i = 2 \\
[x-a,x] \times [y-a,y] & if \; i = 3 \\
[x,x+a] \times [y-a,y] & if \; i = 4 \\
\end{array}
\right.
図で表すとこんな感じです。
図から分かるように各領域は重複しています。
そして、フィルタ適用後の輝度値は、各領域の平均値$m_i(x,y)$と標準偏差$\sigma_i(x,y)$を使って、標準偏差が最も大きい領域の平均値として与えられます。
\Phi(x,y) = m_i(x, y) where \: i=arg \: min_j \: \sigma_j(x,y)
つまり、あるピクセルの値を、周辺の4つの領域の中で最も均質な領域の平均値で置き換えるということです。基本的にフィルタ大きさ$a$が大きいほどより抽象的な画像となります。
計算量
上記のアルゴリズムを愚直に実装しようとした場合、各ピクセルに対する計算量が$2\times4(a+1)^2$ですので、画像一辺のピクセル数を$n$とすると、画像1枚で$8n^2(a+1)^2$の計算量となります。
フィルタサイズ$a$が大きい場合は$O(n^4)$の計算量になります。仮に画像サイズが$1000\times1000$だとすると$10^{12}$回ほどの演算が必要で、Intel Core i5の動作周波数が3.50GHzとかなので、計算に数分かかってしまいます。
そこで、計算量を削減するために2次元累積和を利用します。
累積和とは、配列に対して前処理を行うことで高速に区間和を求めることができるアルゴリズムです。
2次元の場合は、ある位置より左上にある全ての要素の和を算出した配列を事前に求めておいて、これを使って領域の和を算出します。
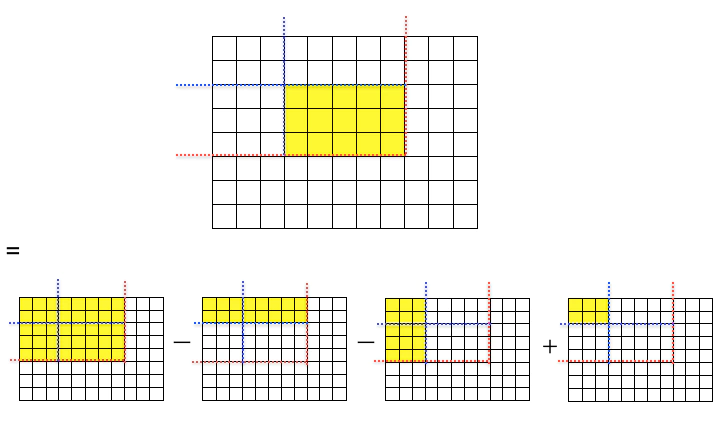
こちらの記事が非常に分かりやすいので引用させて頂きますが、以下の図のように二次元累積和を利用することで、画像内の黄色区間の和を$O(1)$で算出できます。
一方でKuwaharaフィルタでは、領域内の輝度値の平均値だけでなく標準偏差も算出する必要があります。ですが、標準偏差は以下のように式変形できるので、二乗和と和の累積和の配列さえ事前に用意しておけば標準偏差も同様に計算量$O(1)$で算出できます。
※画像の各ピクセルの輝度値(0~255)は非負で、$\sigma$が最小のとき$\sigma^2$も最小です
\sigma= \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x} )^2\\
=\frac{1}{n} \sum_{i=1}^{n} x_i^2 - \frac{1}{n} \sum_{i=1}^{n} 2x_i \bar{x} + \frac{1}{n} \sum_{i=1}^{n} (\bar{x})^2\\
=\frac{1}{n} \sum_{i=1}^{n} x_i^2 - 2(\bar{x})^2 + (\bar{x})^2\\
=\frac{1}{n} \sum_{i=1}^{n} x_i^2 - \frac{1}{n^2}\Bigl(\sum_{i=1}^{n}x\Bigr)^2
以上より、二次元累積を利用することでKuwaharaフィルタの計算量は、事前計算を含めても$O(n^2)$となり、$1000\times1000$の画像でも計算量が$10^6$回程度で1秒以内で計算することが可能です。
実装コード
実装コードを以下はGithubレポジトリにあります。
※処理に時間がかかる場合はリサイズするか、Web Workerでマルチスレッド化が推奨
参考
・Kuwahara filterとかいう明らかに日本人の名前な画像フィルターに出会い、試してみたらすごかったので紹介する。
・累積和を何も考えずに書けるようにする!