前回のブログでは、手書き文字データの速度改善を行うにあたって、誤差逆伝播法に触れました。
その中では計算グラフや連鎖率のお話、また加算ノードや乗算ノードでの逆伝播がどのようなオペレーションになるのか確認しました。
今回はその続きで、ニューラルネットワークでの以下の演算ノードが、逆伝播でどのような処理になるのかを確認します。
・シグモイド関数（活性化関数）
・Softmax関数
・交差エントロピー誤差（損失関数）
・Affine変換（行列の内積とバイアスの和）
\def\textlarge#1{%
{\rm\Large #1}
}
\def\textsmall#1{%
{\rm\scriptsize #1}
}
シグモイド関数の逆伝播
シグモイド関数は以下のような形の関数でした。
y = \frac{1}{1+e^{-x}}
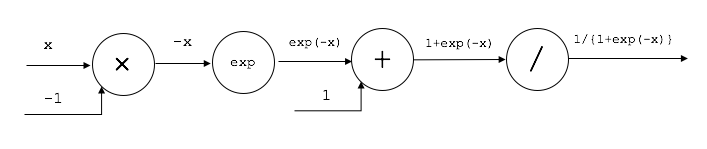
これを計算グラフで表現してみます。
シグモイド関数自体が、加算、除算、指数計算の複合計算なので、計算ノードが複数組み合わさったものになります。
順伝播は以下のような形です。
逆伝播ですが、まずは最後の除算ノードに着目します。
除算は、y=1/x という演算処理なので、偏微分は以下の計算になります。
\frac{\partial y}{\partial x} = -\frac{1}{x^2} = -y^2
その手間の3つめの加算ノードは前回お話ししたとおり、そのまま値を流すだけです。
その次の指数計算「exp」ノードについては、偏微分計算は以下の通りです。
\frac{\partial y}{\partial x} = e^x
つまり、この場合はexp(-x)をかけて逆伝播します。
最後の逆伝播は一番手前の乗算ノードになりますが、前回お話しした通り、
入力ノードをひっくり返して掛ければ良いので、この場合は-1をかけてやれば良いことになります。
整理すると以下のような計算グラフになります。
逆伝播の最後の出力は、以下のように表現を変えることができます。
y^2e^{-x}\frac{\partial E}{\partial y}=y\frac{e^{-x}}{1+e^{-x}}\frac{\partial E}{\partial y}= y(1-y)\frac{\partial E}{\partial y}
なので、シグモイド関数のノードでは、順伝播で出力された値yに対して、y（1-y）倍した値を
逆伝播で渡してやれば良いことになります。
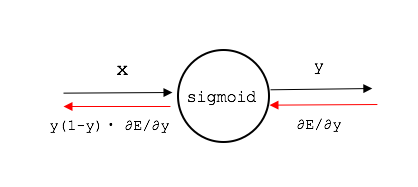
Softmax関数の逆伝播
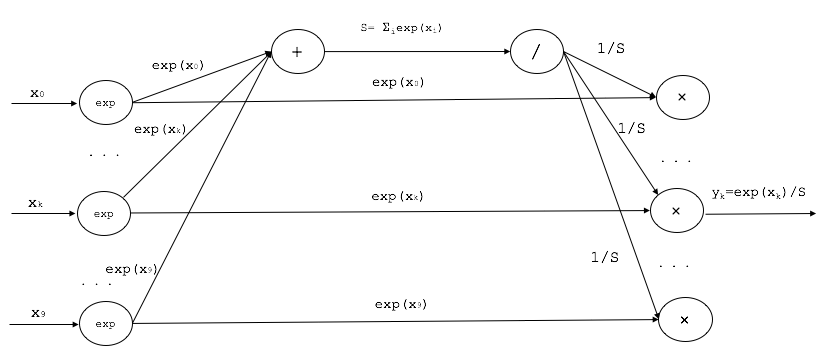
Softmax関数はこのような形をしていました。
y_{k}=σ(k)=\frac{e^{x_{k}}}{\sum_{i=0}^9(e^{x_{i}})}
計算グラフは、このような形になります。
逆伝播については、若干複雑です。
今まで出てきた加算/乗算/除算/指数のノードを組み合わせるとできるわけですが、結果から先に記載すると、インデックスk番目に着目した計算結果は以下の通りです。
y_{k}(\frac{\partial E}{\partial y_{k}}-{\sum_{i=0}^9 y_{i}\frac{\partial E}{\partial y_{i}}})
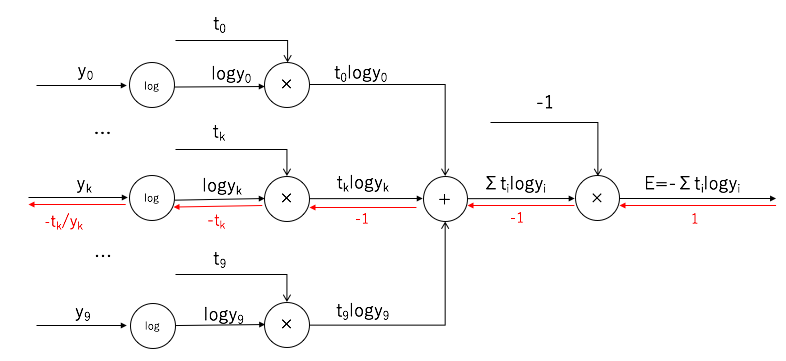
逆伝播のフローを赤線で記載すると以下のような計算結果になります。
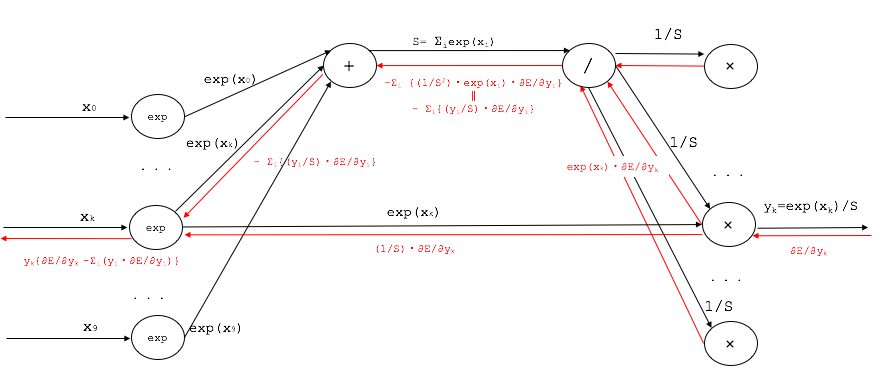
入出力だけに着目して表現するとSoftmaxノードは以下のような表現になります。
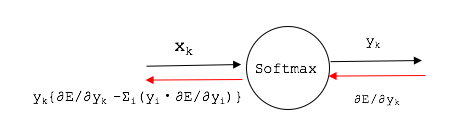
Softmaxの逆伝播の形は、この後に説明する「交差エントロピー誤差」の逆伝播と組み合わせると、実は非常にスッキリした形になります。
話を進めていきます。
交差エントロピー誤差関数の逆伝播
交差エントロピー誤差の関数はこのような形をしていました。
E=\sum_{n=1}^N(-log(y_{n,t_n}))
この表現は、n番目の入力データをx$\textsmall{n}$とし、それに対する正解データをt$\textsmall{n}$（=0,1,2,...,9）、
そしてその時に出力層からの10個の数値y$\textsmall{n,k}$（k=0,1,2,...9）で定義したときの形でした。
上記はN個のバッチデータを扱う表現ですが、逆伝播を考えるときは、1つの入力データを入力したケースを考えます。
つまり、入力データをx（ベクトル）、 出力データをy（ベクトル）、正解データをt（スカラー）としたときの表現は以下のようになります。
E=-log(y_{t})
ここでの正解データtはスカラー値ですが、正解のインデックスが1で他は0という「one-hot表現」ベクトルを用いてみます。
たとえば、正解が3である場合には、正解データtは以下のようなベクトル値で表現します。
t=(0,0,0,1,0,0,0,0,0,0)
one-hot表現を用いた場合の、交差エントロピー誤差は以下のような表現となります。
E=\sum_{k=0}^9(-t_{k}log(y_{k}))
対数関数の微分は以下の通りです。
\frac{d}{d x} ({log(x)}) = \frac{1}{x}
計算グラフは以下のようなフローになります。
つまり、インデックスkでの逆伝播の出力は以下の通りです。
-\frac{t_{k}}{y_{k}}
「交差エントロピー誤差」ノードという括りで見たときには、インデックスkの入出力は以下のような表現になります。
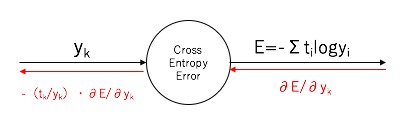
「Softmaxノード」と「交差エントロピー誤差ノード」の逆伝播結合
上記で計算した、「Softmaxノード」と「交差エントロピー誤差ノード」の逆伝播を結合してみます。
つまり、計算としては「Softmaxノード」の逆伝播の以下の結果に対して、
y_{k}(\frac{\partial E}{\partial y_{k}}-{\sum_{i=0}^9 y_{i}\frac{\partial E}{\partial y_{i}}})
これを以下の置換を行うことで計算できます。
\frac{\partial E}{\partial y_{k}} → -(\frac{t_{k}}{y_{k}})\frac{\partial E}{\partial y_{k}}\\
\frac{\partial E}{\partial y_{i}} → -(\frac{t_{i}}{y_{i}})\frac{\partial E}{\partial y_{i}}
つまり、「交差エントロピー誤差ノード」の逆伝播の出力を、「Softmaxノード」の入力値に与えてやります。
あと、one-hot表現している正解データtについては、k番目の要素が1で他は
0であることを注意して、計算してみると以下のようになります。
y_{k}\bigl((-\frac{t_{k}}{y_{k}})\frac{\partial E}{\partial y_{k}}-{\sum_{i=0}^9 y_{i}(-\frac{t_{i}}{y_{i}})\frac{\partial E}{\partial y_{i}}}\bigl) \\
=-t_{k}\frac{\partial E}{\partial y_{k}}+y_{k}\sum_{i=0}^9 t_{i}\frac{\partial E}{\partial y_{i}} \\
=-t_{k}\frac{\partial E}{\partial y_{k}}+y_{k}\frac{\partial E}{\partial y_{k}} \\
=(y_{k}-t_{k})\frac{\partial E}{\partial y_{k}}
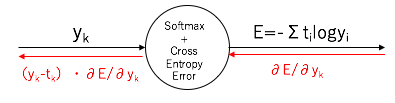
上記の結果のとおり、「Softmaxノード」と「交差エントロピー誤差ノード」を結合した場合の、逆伝播は(y$\textsmall{k}$-t$\textsmall{k}$)倍して渡してやるだけという非常にシンプルな結果になりました。
実は、このような逆伝播の結果がシンプルな形になるように、Softmax関数、交差エントロピー誤差関数は設計されています。
プログラムを組む際のアルゴリズムも、この2つを1つのノードとして扱った方がシンプルになります。
ノードのイメージはこのような形になります。
Affine変換の逆伝播
最後にAffine変換（行列の内積とバイアスの和）のノードの逆伝播を紹介します。
入力層をX、重み付けパラメータをW、バイアスをBとしたとき、出力Yは以下のような
演算であることを以前のブログで説明いたしました。
Y=X・W+B
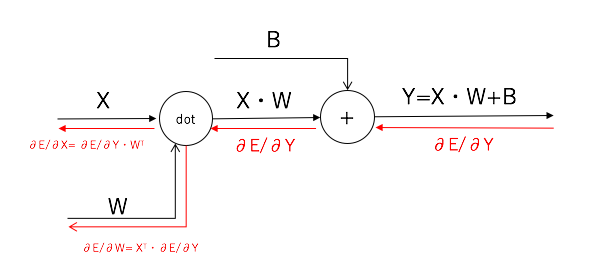
上記のような行列の内積と和から成る演算がAffine変換ですが、これを計算グラフで表すと以下のようになります。
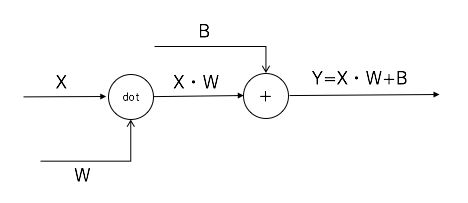
内積計算は「dot」ノードで表現しています。
入力層X、重み付けパラメータWに対応する逆伝播の計算ですが、計算の詳細は割愛しますが、
結果は以下のような形となります。
\frac{\partial E}{\partial X} = \frac{\partial E}{\partial Y}・W^T \\
\frac{\partial E}{\partial W} = X^T・\frac{\partial E}{\partial Y}
形としてはこちらも非常にシンプルな演算式となっています。
XとWの右上の「T」は転置行列であることを意味しています。
また、ここで∂E/∂X、∂E/∂W、∂E/∂Yなどは要素での偏微分の行列を表しています。
たとえば、∂E/∂Xについては以下のような形の勾配ベクトルになります。
\frac{\partial E}{\partial X}=(\frac{\partial E}{\partial X_{0}},\frac{\partial E}{\partial X_{1}},...)
逆伝播を加筆した計算グラフは以下の通りです。
前回と今回のブログで、計算グラフという考えかたを導入して、
ニューラルネットワークの入力層から損失関数計算までの
各フェーズでの逆伝播を確認しました。
この議論の最初に、アルゴリズムの速度改善のためには、損失関数Eの最小値を、如何に早く計算するかが肝になってとお話ししましたが、
実は、損失関数として導入している「交差エントロピー誤差」自体が、
逆伝播で最小値を早く計算するために設計されています。
また、各計算ノードでの逆伝播はシンプルな局所計算で実現でき、
それらを組み合わせることで、速度改善につながるところも垣間見えます。