前回のブログでは、scikit-learnのdatasetsにある手書き文字データを用いて、シンプルなニューラルネットワークの実装と、認識精度の向上の推移を可視化してみました。
ただ、前回のような数式主体のアルゴリズムは、プログラム的にはシンプルなものになりますが、時間的なコストもかかってしまう問題がありました。
今回から数回に分けて、誤差逆伝播法(バックプロバケーション)を用いた、速度改善を進めていきます。
速度改善が求められるところ
ニューラルネットワークのアルゴリズムは、損失関数の交差エントロピー誤差Eを最小にするパラメータωを、勾配法で求めるものです。
ω \Leftarrow ω-\eta\frac{\partial E}{\partial ω}
速度改善が求められるのは、上記の∂E/∂ω の勾配計算の部分です。
この勾配計算の処理速度を改善していきます。
計算グラフ
誤差逆伝播法の話をする前に、計算グラフという考え方に触れておきます。
簡単な例として以下のような例題をあげてみます。
100円(税抜)のりんごを5個購入したときの支払金額を求めなさい。
ただし消費税は8%とする。
計算グラフではノードと矢印で計算過程を表現します。
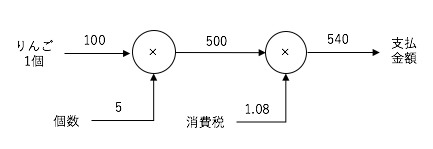
上記の例は以下のような表現になります。
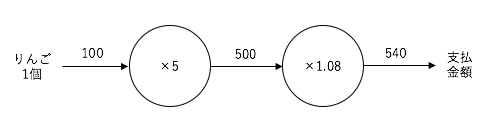
りんご100円の金額が、5個購入の「×5」のノードに流れ、さらに消費税の「×1.08」のノードに流れる、局所的な計算の伝播が行われる表現が「計算グラフ」です。
上記の表現では、入力パラメータはりんご1個でしたが、個数や消費税も入力パラメータと考えると、以下のような計算グラフで表現されます。
この表現ではノードが汎用的な乗算ノード「×」に変化しています。
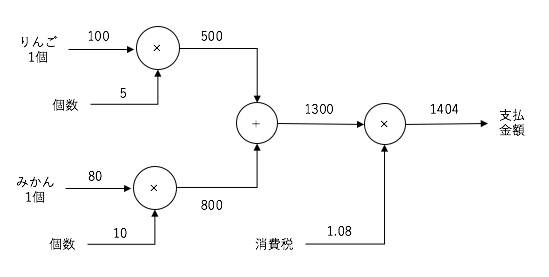
また、追加で80円のみかんを3個買うような場合、以下のような表現になります。
このように、局所的な単純計算のノードで、計算結果を伝播していくモデルが
計算グラフという表現です。
計算グラフには、複雑な計算を単純な計算に紐解く効果と、各計算段階を保持できるメリットがあります。
ただそれだけだと、計算グラフを導入するメリットの実感は薄いかもしれません。
計算グラフの実際の大きなメリットは、これからお話する逆伝播を用いることで、勾配計算∂E/∂ωの効率的に行える部分にあります。
話を進めていきます。
計算グラフでの逆伝播
先ほどの計算グラフでは、各ノードで計算を行いながら、計算結果を左から右へ伝播していく流れとなっていました。
この左から右への前方向の計算伝播を順伝播(forward probacation)と呼びます。
それに対して、右から左への計算伝播があります。
これが、逆伝播(backward probacation)と呼ばれる計算フローです。
具体的にどんな計算を行うのでしょうか?
たとえば、先ほどの買い物の例でいうと、りんごの1個の価格が1円上がったときに、支払い金額はどのくらい変動するかを計算します。
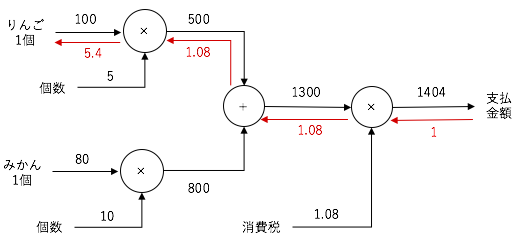
先に、逆伝播で渡される数値だけ赤線/赤字で記載してみます。
右末端の数字「5.4」がりんごが1円上がったときの、支払金額の変動値です。
言い換えれば、りんごの値段に対する支払金額の勾配値(微分値)です。
なぜ、赤線のような数値で計算伝播されていくのかを次に説明します。
連鎖律(Chain Rule)
計算グラフを眺めると、各ノードに対して入力変数があり、また計算した結果を次のノードに伝播しています。
りんごの部分に着目して、支払金額までの順伝播の計算をみてみます。
まずは、りんごをx, 個数をyとしたときの結果をsとすると、最初の乗算ノードの関数は以下のような形になります。
s(x,y)= xy
次に、みかんの10個分の金額をtとすると、りんご5個分の金額sとの合算値をuとすると、加算ノードの計算は以下のようになります。
u(s,t) =s+t
最後に、消費税をvとしたときの、最終的な支払金額をEとすると、乗算ノードの形は以下のようになります。
E(u,v) =uv
つまり、支払金額の計算はs(x,y)、u(s,t)、E(u,v)の合成関数となっています。
ここで、りんごの金額xに対する支払金額Eの値上値は、以下の計算(偏微分)を行うことになります。
\frac{\partial E(u,v)}{\partial x}
ここで、合成関数Eの偏微分は、次のような表現で偏微分の積に分解できます。
\frac{\partial E(u,v)}{\partial x}=\frac{\partial s(x,y)}{\partial x}×\frac{\partial u(s,t)}{\partial s}×\frac{\partial E(u,v)}{\partial u}
3つの偏微分に分解された各項目を見てみると、以下の計算グラフとの対応は以下の通りです。
∂s/∂x ⇒ 乗算ノード(りんご5個分の金額計算)
∂u/∂s ⇒ 加算ノード(りんご5個とみかん10個の金額加算)
∂E/∂u ⇒ 乗算ノード(消費税の金額計算)
各ノードで実行する局所関数の偏微分を掛け合わせたものになっていることが、わかるかと思います。
次に、加算ノードと乗算ノードの偏微分が具体的にどんな値をとるのかを見てみます。
加算ノードの偏微分
加算ノードでは、以下のような計算をしますが、
z=x+y
x, yのそれぞれの偏微分は以下の通りです。
\frac{\partial z(x,y)}{\partial x} = 1 \\
\frac{\partial z(x,y)}{\partial y} = 1
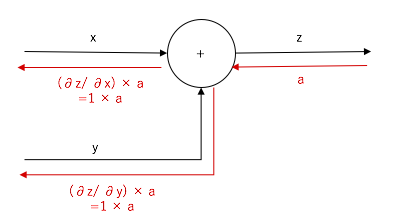
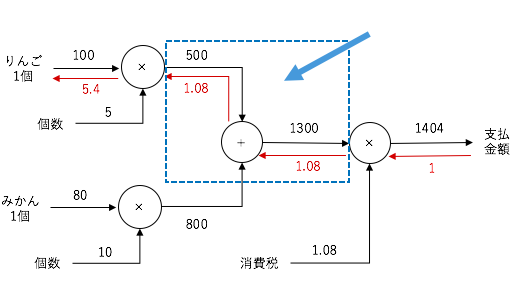
つまり、右からの伝播に関しては、値をそのまま伝播してやれば良いことになります。
先ほどの、りんごとみかんの支払金額のグラフでは以下の箇所に該当します。
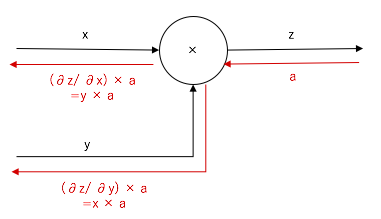
乗算ノードの偏微分
乗算ノードでは、以下のような計算をしますが、
z=xy
x, yのそれぞれの偏微分は以下の通りです。
\frac{\partial z(x,y)}{\partial x} = y \\
\frac{\partial z(x,y)}{\partial y} = x
つまり、右からの伝播に関しては、順伝播の入力の反対側の値を掛けてあげるだけです。
先ほどの、りんごの支払金額のグラフでは以下の箇所に該当します。
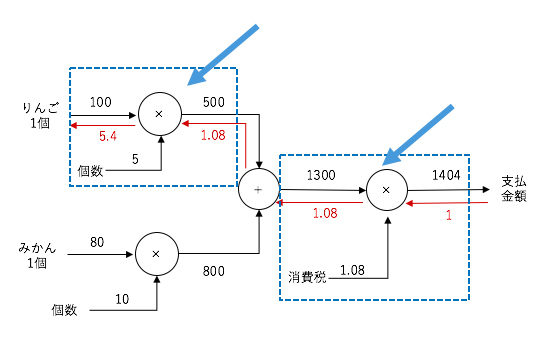
今後の流れ
今回はりんごの買い物の例で、計算グラフを用いた逆伝播(backward probacation)を説明しました。
このように、計算グラフの逆伝播処理で、微分演算をしなくても、各ノードへの入力値の単純演算の繰り返しで、りんごの値段に対する支払金額の値上率(勾配)を求めることができます。
加算ノードと乗算ノードを組み合わせれば、もちろんこれよりも複雑な勾配計算も対応することもできます。
ただ、今回は加算と乗算の2種類のパターンのみの紹介でした。
ニューラルネットワークでは、今後以下の関数に対しての演算ノードが必要になります。
・シグモイド関数(活性化関数)
・Softmax関数
・交差エントロピー誤差(損失関数)
・Affine変換(行列の内積とバイアスの和)
上記の演算ノードに対応することで、誤差逆伝播法が完成します。
計算自体は指数演算や対数演算が入るなど、少々複雑な形をしているものもありましたが、逆伝播での各ノード演算結果(偏微分)はシンプルな形になります。
上記の詳細については、次回にお話ししたいと思います。
Softmax関数や交差エントロピー誤差のような特殊な関数は、
実は逆伝播を簡易に行うために、意図的に用意されたものであることが、
次回で垣間見えて来るかと思います。