前回のブログでは、scikit-learnのdatasetsにある手書き文字データで分類器のパフォーマンスチェックを行いました。
今回は同じ手書き文字データを用いて、ニューラルネットワークで学習させるサンプルプログラムを作ってみます。
\def\textlarge#1{%
{\rm\Large #1}
}
\def\textsmall#1{%
{\rm\scriptsize #1}
}
ニューラルネットワークについて
言わずと知れた、脳神経のモデルになります。
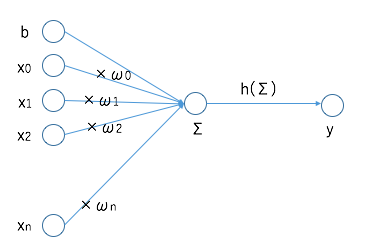
例えば、n個のノードから信号xを受け取り、信号に対して係数ωでの重み付け、バイアスbでの加算の重み付けをした総和を、活性化関数hに与えます。
活性化関数hでは出力判定を行います。
数式ではこのような表現をします。
y=h(\sum_{i=0}^n(ω_{i}x_{i})+b)
ニューラルネットワークは例えば、2つの入力信号、1つの出力に対するものは以下のような、数式表現をします。
y = h(ω_{0}x_{0}+ω_{1}x_{1}+b)
活性化関数は以下のような、ステップ関数、ランプ関数、シグモイド関数があります。
今回、活性化関数はシグモイド関数を用いることにします。
h(x) = \frac{1}{1+e^{-x}}
今回のニューラルネットワークモデル
手書き文字は8×8のイメージデータでした。
各イメージは64個の数値のアレイです。
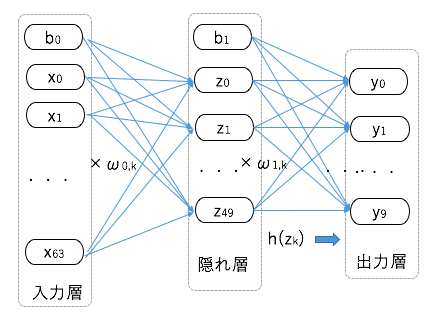
このことから、入力層のノードは64個。
0〜9の数値に分類するので、出力層には10個の出力ニューロンを設けます。
また、今回は50個のニューロンを持つ隠れ層を設ける形をとります。
入力層/隠れ層にはバイアスb$\textsmall{0}$,b$\textsmall{1}$を与えます。
イメージは以下の通りです。
バッチ入力
入力層のノード数はバイアスを除くと64個ありますが、イメージデータは複数ありますので、行列演算でまとめて処理した方が効率的です。
例えばイメージデータがN個ある場合は、入力データXは N行×64列のデータ。
バイアスb$\textsmall{0}$はN行×1列のデータ。
重み付けパラメータω$\textsmall{0}$は、64行×50列の行列パラメータ。
隠れ層はN行×50列のデータ。出力層はN行×10列のデータとなります。
また、例えば入力層(X)から隠れ層(Z)への行列演算は、
内積演算「・」で、以下のように表現できます。
Z = X・ω_{0}+b_{0}
SoftMax関数
出力層にはニューロンが10個ありますので、当然ながら10個のアウトプットがあります。
このモデルでは入力されたイメージが、0~9の数字のどれに該当するかを分類するので、
出力数値も0〜1までの値の比率的な値にした方が扱いやすくなります。
このとき導入するのが、SoftMax関数です。
k番目の出力に対しては以下のような値を計算します。
σ(k)=\frac{e^{y_{k}}}{\sum_{i=1}^⒑(e^{y_{i}})}
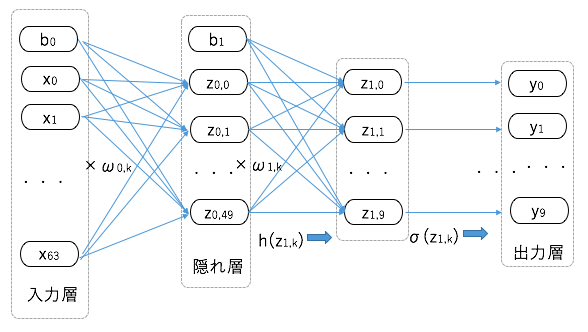
SoftMax演算σを作用させるところを層で表現する場合は、
ネットワークは以下のようなイメージになります。
損失関数
ニューラルネットワークでは、各層の間に作用させる重み付けパラメータのωを最適化する計算を行います。
その上で指標となるのが損失関数（Loss Funtion）です。
最適化は損失関数が最小値になるようにωを調整する処理を行います。
損失関数の種類はいくつかありますが、ニューラルネットワークで分類を行う場合は、「交差エントロビー誤差」を用います。
今回のケースに関しては、手書き文字データには、その文字が何の数字なのかの正解データが用意されていました。
n番目の入力データをx$\textsmall{n}$とし、それに対する正解データをt$\textsmall{n}$（=0,1,2,...,9）とします。
また、その時に出力層からの10個の数値をy$\textsmall{n,k}$（k=0,1,2,...9）で表現すると、交差エントロピー誤差は以下の計算式になります。
E=\sum_{n=1}^N(-log(y_{n,t_n}))
y$\textsmall{n,k}$は、0~1の値をとるので、その対数をとった値は負の数になります。
そして、その対数にマイナスをかけて総和しているので、全体の値は正になります。
この交差エントロピー誤差の値が最小になるように、各層の重みパラメータω$\textsmall{0,k}$, ω$\textsmall{1,k}$の最適化計算を行います。
勾配法
交差エントロピー誤差の最小値を求める場合には勾配法を用います。
最小値のような極値を持つと想定される関数f(x)に対して、xを以下のように順繰りに変化させて最小値を求める方法です。
x \Leftarrow x-\eta\frac{df}{dx}
ηは学習率と呼ばれる正の値です。
関数の傾き df/dx に対して、逆方向にxを動かしていくので、関数の凹みに到達するとイメージしてもらえればと思います。
今回は交差エントロピー誤差Eは、複数の重み付けパラメータω$\textsmall{n,k}$の関数になっています。
なので、今回は各ω$\textsmall{n,k}$について、以下のような処理を行います。
ω_{n,k} \Leftarrow ω_{n,k}-\eta\frac{\partial E}{\partial ω_{n,k}}
ちなみに、∂E/∂ω$\textsmall{n,k}$ は偏微分を行った値です。
また、これらの要素が並んだベクトル（∂E/∂ω$\textsmall{n,0}$, ∂E/∂ω$\textsmall{n,1}$, ..., ∂E/∂ω$\textsmall{n,M}$）を勾配ベクトルと呼びます。
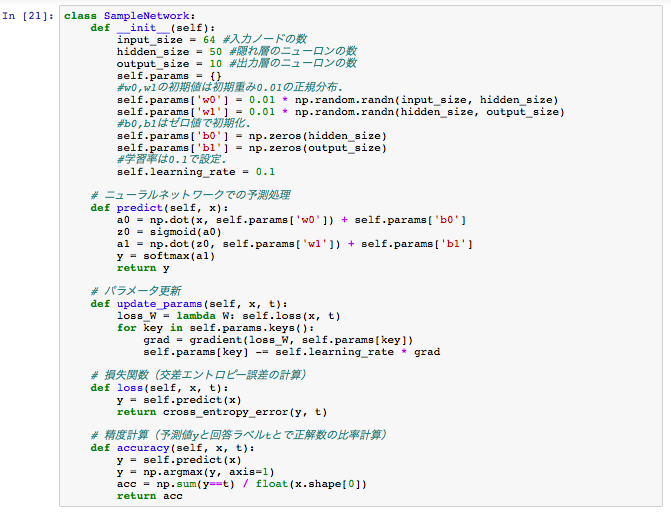
プログラム
今回のニューラルネットワークのモデルと、必要とするアルゴリズムのポイントを上記で簡単に説明しました。
実際にプログラムで、ニューラルネットワークが繰り返しのデータ入力で、交差エントロピー誤差が減少し、認識精度が上がっていく様子をグラフで表示してみます。
まずは、必要なライブラリをインポートします。
今回、解析で使用する関数群を用意します。
次にニューラルネットワークのクラスを用意します。
手書き文字データをロードします。
訓練データとテストデータに分割します。
今回は、訓練データからランダムで100個のデータをピックアップしてバッチ入力し、それを300回繰り返した場合の、損失関数（交差エントロピー誤差：cross entropy error）と認識精度（accuracy）の推移を確認します。
また同時に、テストデータでの認識精度（accuracy）も確認して、精度のブレや過学習が起きていないかも確認します。
ニューラルネットワークを作成します。
繰り返し処理のための各種変数を準備します。
認識精度の計算については、毎回の繰り返し処理では行わず、訓練データの数をバッチ数100で割った頻度（エポック単位）で計測します。
繰り返し学習処理を行います。
バッチデータを作成し、ニューラルネットワークに投入し、内部パラメータを更新していきます。その際に損失関数の値の計測と、認識精度の計測を行っています。
記録した損失関数値と、認識精度値（訓練データ/テストデータ）をグラフで表示します。
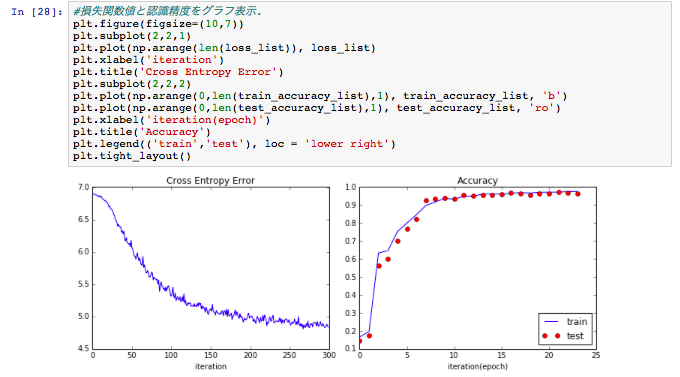
繰り返し頻度が増えるごとに、損失関数の交差エントロピー誤差（Cross Entropy Error）の減少と、認識精度（Accuracy）のアップが確認できるかと思います。
また、認識精度については、青線の訓練データの値と、赤点のテストデータの値も近い値になっており、ニューラルネットワークが適切な学習がなされていることも確認できます。
今回のサンプルコードは300回の繰り返し処理ですが、MacBook Airで10分〜15分程度の時間がかかりました。
微分などの数式を用いたアルゴリズムは比較的シンプルなものになりますが、時間的なコストもかかってしまいます。
これについては、誤差逆伝播法（バックプロバケーション）を用いることで、速度改善ができます。
今回はここまで！