はじめに
前回に引き続き、ハワイで開かれた国際会議(AAAI2019)で発表した論文を宣伝します！
(写真は、学会会場から歩いて5分のビーチで撮った夕日です)
元論文は
Liyuan Xu, Junya Honda, Masashi Sugiyama, "Dueling Bandits with Qualitative Feedback", Proceeding of the 23rd AAAI Conference on Artificial Intelligence (AAAI2019), 2019.
[PDF]
この論文では、「質的フィードバックを用いた比較バンディット」という新しい問題を提案したのですが、この記事では「比較バンディット」について紹介したいと思います。論文はこの「比較バンディット」を外部情報を用いて効率的に行う手法を提案しました。
ざっくりとした説明
「比較バンディット」（Dueling Bandit）とは、バンディット問題において、具体的な報酬は得られないものの、二本の腕を比較できるときに、その比較において最も良い腕をできるだけ多くプレイするにはどうすればよいか、という問題です。ここでは「街で一番のラーメン屋を見つける」という問題を題材に、比較バンディットがどういうものかを説明します。
通常の多腕バンディット
比較バンディットに入る前に、通常のバンディットについて少し話させてください。前回の記事でも書いたとおり、バンディット問題では「腕」と呼ばれるスロットマシンたちを考えます。
この$K$本の腕をagentと呼ばれるプレイヤーが順次プレイし、報酬を得ていくのが一般にバンディットと呼ばれる問題です。前回は$K$本の中から最も期待報酬の大きい腕を見つけるという最適腕識別問題を考えたのですが、今回はリグレット最小化問題と呼ばれる別の問題を考えてみましょう。
リグレット最小化問題というは以下のような問題です。
今、みなさんがカジノのオーナーと仲良くなって「カジノにあるスロットマシン、なんでも好きなもの合わせて100回プレイしていいよ」と大変太っ腹な提案をされたとします。こんな時には、いくら友達が経営しているカジノであったとしてもできるだけ稼ごうとするのが礼儀だと僕は信じています。（太っ腹な提案、いつでもお待ちしています。）もちろん、どのスロットマシンが当たりやすいかは最初わからないですが、その中でも予め決められたプレイ回数での報酬の合計を最大化するというのがリグレット最小化問題です。
リグレット最小化問題
「一番稼ぐ」といっても、選択肢が限られている以上無限に稼げるわけではありません。実際、「常に最も期待報酬の高い腕をプレイし続ける」以上に稼ぐことは不可能なことは明らかでしょう。そのため、我々の目標は常に最も期待報酬の高い腕をプレイし続けたときの合計報酬に可能な限り近づく、ということになります。この**理想的な場合での報酬の合計と、現実に得られた成績の差をリグレットと呼びます。
リグレットの具体的な定義は以下のとおりです。
$$\large \text{Regret} = \color{blue}{T\mu^*} - \color{red}{\sum_{t=1}^T r_t}$$
いま、$T$を総プレイ回数、$\mu^*$を最も期待報酬の高い腕の高い腕の期待報酬、$r_t$を$t$回目のプレイで得た報酬であるとしています。この時に青い部分$T\mu^*$が最も良い腕をプレイし続けた時の期待報酬であり、赤い部分$\sum_{t=1}^T r_t$が実際に$T$回のプレイで得られた報酬になります。この差がRegretと呼ばれるもので、これを最小化するのが目的です。つまり、 あとになってオーナーに実は あの腕が一番良かったんだよと聞かされた時の「後悔」を最小化するというのが目的となっています。有名なアルゴリズム（UCB、Thompson Samplingなど[解説記事]）はこのリグレット最小化を目的としていてすべて$\text{Regret} = O(\log T)$を達成するアルゴリズムであることが知られています。
ラーメン屋の「報酬」ってなんだ？
では一番いいラーメン屋見つける問題をバンディット問題として定式化しましょう。
いま、$K$軒のラーメン屋に合計$T$回通うとします。最初はどのラーメン屋が美味しいかわからないですが、その中でもできるだけ美味しいラーメンを食べたいとします。そのため、いろいろなラーメン屋に通いながらどれが美味しいか探索していく必要があります。ここまでは「スロットマシン ＝ ラーメン屋」、「プレイする = ラーメンを注文する」とすれば完全にバンディット問題となります。しかし、ここで問題なのが「美味しさ」の数値化がとても難しいということです。また、ラーメン屋の魅力はひとえにラーメンの美味しさで決まるものではありません。「コスパ」「接客の良さ」「雰囲気」などなど色々なもので決まります。このようなことを考えるとスロットマシンで明らかだった「報酬」の定義が難しいということがわかります。
比較バンディット (Dueling Bandit)
この「報酬」の定義の難しさを解消したのが比較バンディット (Dueling Bandits)です。ここでは、各腕の報酬ではなく、２つの腕の比較によりリグレットを定義しそれを最小化します。
実際、ラーメン屋を決めるときにはラーメン屋単体で考えるよりも、「あそこのラーメンより美味しい」「近所のラーメンのほうが安い」というように常に比較で考える事が多いですよね。このように、具体的に数値で評価しにくいことも、他の選択肢との比較は容易にできる、というのがアイデアの味噌です。そのため、比較バンディットでは毎回２つの腕を選び、どちらの腕がよかったかというフィードバックを元に最も「良い」腕を選び取るというアルゴリズムです。
質的フィードバックをもとにした比較バンディット
比較バンディットにおいては、同じ人に「２つのラーメン屋でどちらが良かったか」と聞いていました。
しかし、実際僕らはラーメン屋を点数で評価しています。例えば食べログでは、五点満点のスコアでラーメン屋を評価します。 このとき、点数はなにかの「量」を表しているわけではありません。 4点のラーメンが2点のラーメンよりも倍美味しいということはないのです。このスコアはあくまで、ラーメン屋が「4点」と言われたときに、それが「2点」のものよりも良い、ということしか情報として含みません。このように数字が量ではなく、順序が大事なフィードバックのことを質的なフィードバックといいます。この質的フィードバックをもとにした比較バンディットについてはじめて議論したのが、自分の論文です。
比較バンディットの応用例：検索アルゴリズムの最適化
この比較バンディット、最も成功した応用例は、下の論文で提案された検索アルゴリズムの最適化です。
Filip Radlinski, Madhu Kurup, Thorsten Joachims. "How does clickthrough data reflect retrieval quality?". Proceedings of the 17th ACM conference on Information and knowledge management (CIKM2008). 2008
[PDF]
ここでは検索アルゴリズムの最適化を比較バンディットにより行う手法が提案されています。ユーザー$u$がクエリ$q$で検索した時、下図のように検索アルゴリズムが２つ$f_1(u,q), f_2(u,q)$選ばれ、それぞれが検索結果$r_1$と$r_2$を返します。システムはこの$r_1$と$r_2$を混ぜてユーザーに表示し、ユーザーがクリックしたページを元にどちらのアルゴリズムが良かったかを評価します。このようにして得られた比較情報から、$K$個の検索アルゴリズムのうち最も良いものを見つけ出すことができます。
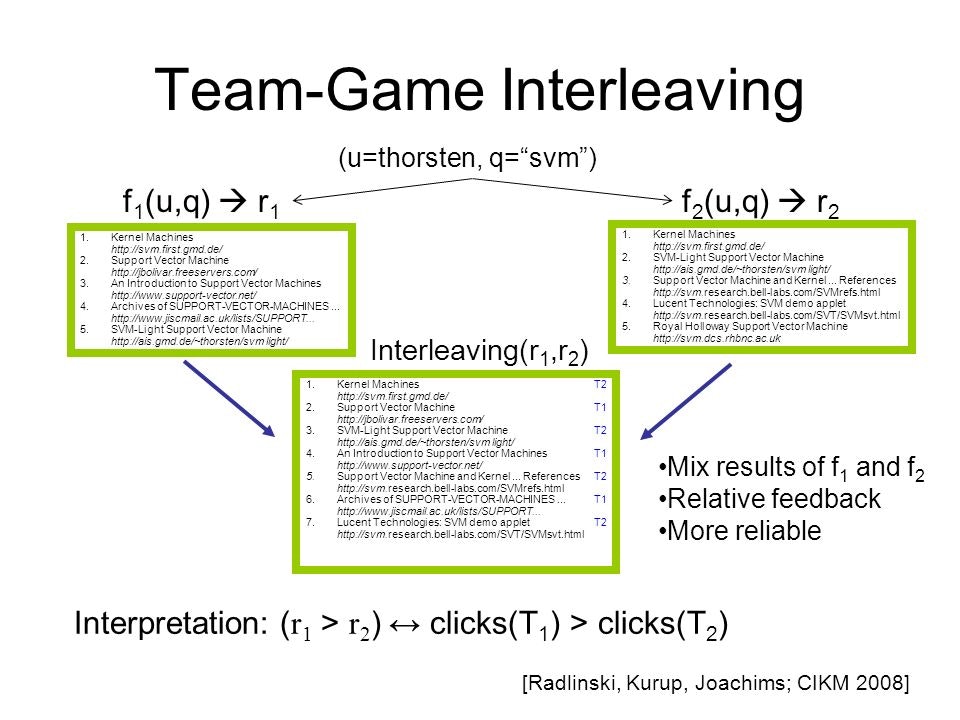(図は https://slideplayer.com/slide/678318/1/images/5/Team-Game+Interleaving.jpg より引用)
もっとくわしく！
ここでは、上のざっくりした説明では物足りない人のためにちゃんと数式を使って問題の定義と目的を述べます。
比較バンディットの定式化
比較バンディットでは$K$本の腕から、各時刻$t$で二つ$(i_t,j_t)$を選択します。すると、選んだ腕の間での確率的な比較の結果$r_t$を観測することができます。ここで、この比較は
$$ \large
r_t = \begin{cases}
1 & (\text{確率}: \mu_{i_t, j_t})\\
0 & (\text{確率}: 1-\mu_{i_t, j_t} )
\end{cases}
$$
として得られるとします。ただし$\mu_{i,j}$は腕$i$が腕$j$に「勝つ」確率で以下を満たすとします
$$\large \mu_{i,i} = \frac12\quad \mu_{i,j} = 1-\mu_{j,i}$$
上の条件は自分に対する勝率は0.5であることと、腕$i$と腕$j$の勝率が足して1となるということを意味します。このもとで、比較で勝つ確率の高い腕「勝者」をなるべく多く選ぶことが目的となります。
比較バンディットにおける勝者
通常のバンディットは期待報酬最大の腕というのが「最も良い腕」でそれをたくさんプレイするのが目的でした。しかし、比較バンディットではそのような「最も良い腕」というのがいつもうまく定義されるとは限りません。具体的には以下腕が３つあり、勝率が下の様になっている例を考えてみましょう。
| 腕１ | 腕２ | 腕３ | |
|---|---|---|---|
| 腕１ | 0.5 | 1.0 | 0.0 |
| 腕２ | 0.0 | 0.5 | 1.0 |
| 腕３ | 1.0 | 0.0 | 0.5 |
このとき、腕１は腕２に常に勝ち、腕２は腕３に常に勝つものの、腕３は腕１に常に勝ってしまいます。比較バンディットにおいては、このような「じゃんけん」のような事が起こってしまうため、どの腕をもっとも良い腕（「勝者」と呼びます）とするのか難しく、実はいろいろな定義があります。今回はその中でもコンドルセ勝者とボルダ勝者を考えます。
コンドルセ勝者
コンドルセ勝者の定義は、すべての他の腕に対して確率1/2以上で勝つ腕です。数式で書くと
$$\large \text{腕}i\text{はコンドルセ勝者} \Leftrightarrow \forall j\neq i \quad \mu_{i,j} \geq \frac12$$
となっています。この定義は直感的ですが、常に存在するとは限りません。特に前の「じゃんけん」の例だと存在しない事がわかります。このコンドルセ勝者を考えた場合、リグレットは、コンドルセ勝者を$a^*_{\text{CW}}$としたとき、
$$\large \text{Regret}_{\text{CW}} = \sum_{t=1}^T \left(\mu_{a^*_{\text{CW}},i_t}-\frac12\right) + \left(\mu_{a^*_{\text{CW}},j_t}-\frac12\right)$$
と定義され、これを最小化するのが目的となります。
ボルダ勝者
ボルダ勝者の定義は、他の腕に対する平均勝率が最も高い腕です。数式で書くと、腕$i$の平均勝率を
$$\large B_i = \frac{1}{K-1} \sum_{k=1}^K \mu_{i,k}$$とおいた時に
$$\large \text{腕}i\text{はボルダ勝者} \Leftrightarrow \forall j\neq i \quad B_i \geq B_j$$
となることです。これはコンドルセ勝者と違い常に存在します。前の「じゃんけん」の例だとすべての腕がボルダ勝者となります。このようなボルダ勝者を考えた時、リグレットはボルダ勝者を$a^*_{\text{BO}}$としたとき、
$$\large \text{Regret}_{\text{BO}} = \sum_{t=1}^T (B_{a^*_\text{BO}} - B_{i_t}) + (B_{a^*_\text{BO}} - B_{j_t})$$
と定義され、これを最小化するのが目的となります。
コンドルセ勝者とボルダ勝者の違い
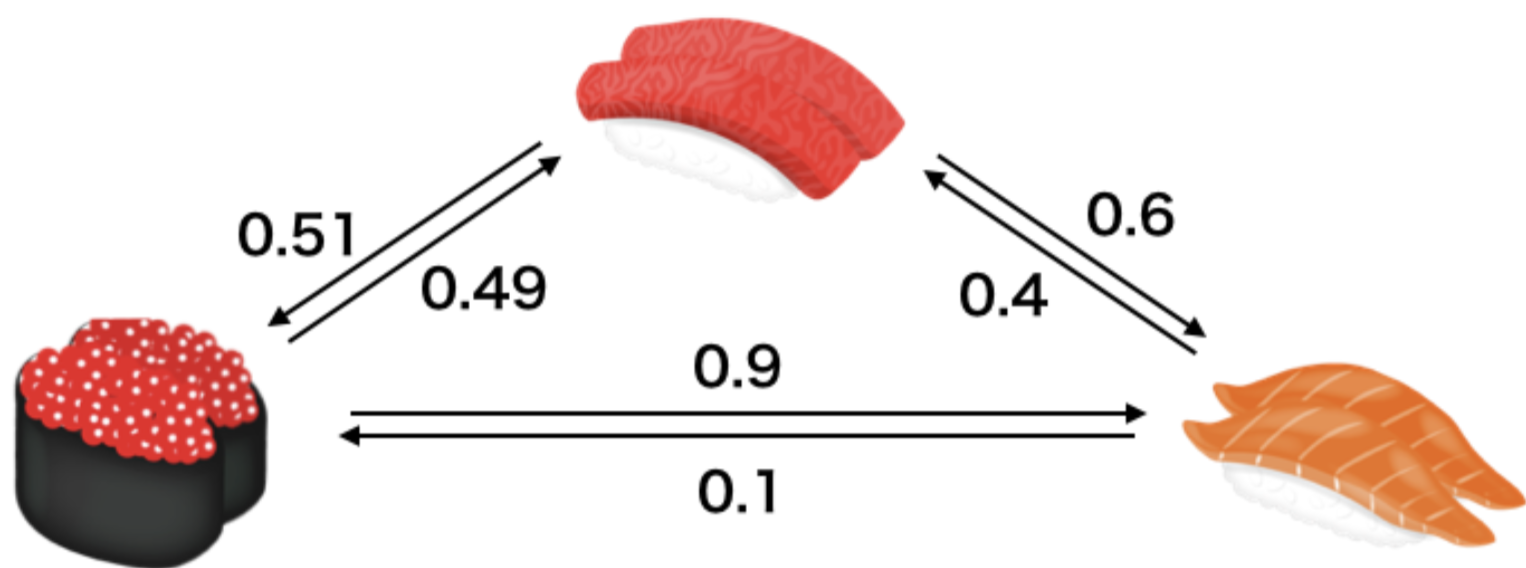
コンドルセ勝者とボルダ勝者の性質の違いを見るために上の例を見てみましょう。今、「寿司のネタでどちらが好きか」という質問をいくら、マグロ、サーモンについて様々な人に聞いてみたとします。その結果上図のような結果になったとしましょう。上では数字は「矢印の根本の方が伸びている先よりも好き」と答えた人の割合です。たとえば「いくらよりサーモンのほうが好きと答えた人は0.1の割合」である事がわかります。
このとき、コンドルセ勝者は「マグロ」です。実際、マグロはいくらとサーモンに対し勝率が0.5を上回っています。しかし、平均勝率を計算してみると、
- 「マグロ」：0.555
- 「いくら」：0.595
- 「サーモン」：0.25
となるため、「いくら」がボルダ勝者となります。
比較バンディットのアルゴリズムについて
ここでは、アルゴリズムについては触れませんがいくつか、参考になるページや論文を紹介します。
コンドルセ勝者を考えたときのアルゴリズム
比較バンディットではコンドルセ勝者を考える設定が最も古く、様々なアルゴリズムが提案されています。自分がこの研究をしていたときには下のレポジトリで公開されているライブラリを使っていました。
C++実装で速く、様々なアルゴリズムが実装されているため、とても便利でした。
ボルダ勝者を考えたときのアルゴリズム
こちらに関しては下の論文を既存手法として扱っていました
Robert Busa-Fekete, Balazs Szorenyi, Weiwei Cheng, Paul Weng, Eyke Huellermeier. "Top-k Selection based on Adaptive Sampling of Noisy Preferences". Proceedings of the 30th International Conference on Machine Learning (ICML2013). 2013
自分で実装したのですが、コード公開は例によって要求があったらで・・・