はじめに
四分位数はデータの分布をおおまかに調べたいときに便利な値です。
この記事では、多量の数値からなるデータからデータの四分位数を求める関数を作ってみて、そのときに考えたことをまとめました。なお、既存のライブラリは使わずに関数を自作することを目標とします。
1. 四分位数とは
四分位数 とは、データを小さい順に並び替えてデータの個数で$4$等分したときの、区切りの位置にある値のことです。
3つの四分位数にはそれぞれ名前がついており、小さいほうから$\displaystyle\frac{1}{4}$の場所にある値を 第1四分位数、$\displaystyle\frac{2}{4}$の場所にある値を 第2四分位数、$\displaystyle\frac{3}{4}$の場所にある値を 第3四分位数 と言い、順に$Q_1,Q_2,Q_3$で表します。なお、第2四分位数はデータの真ん中の値なので、これはデータの 中央値 と同じです。
四分位数の決め方には複数の方法がありますが、今回は数学Ⅰの教科書で採用されている方法を使います。
他の方法も知りたい方は、こちらのサイトを読んでみてください。
以降、小さい順に並んだ$N$個のデータについて、先頭のデータを$0$番目として、先頭から$i$番目のデータを$A[i]$で表します。
第2四分位数(中央値)の求め方
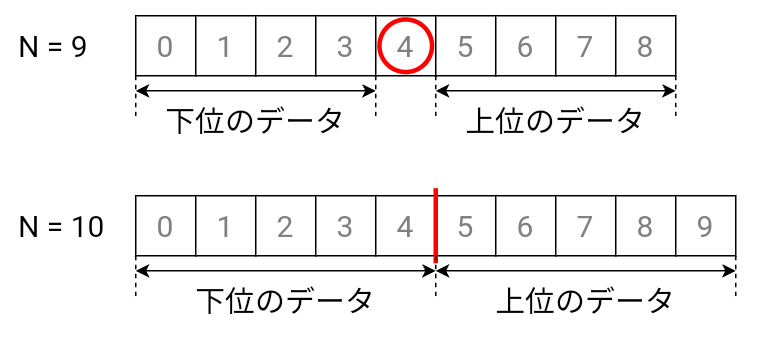
データの個数が奇数の場合は、中央のデータが存在するのでその値が$Q_2$となります。一方、データの個数が偶数の場合は、中央のデータが存在しないので、中央にもっとも近い2個のデータの平均値が$Q_2$となります。
第1四分位数,第3四分位数の求め方
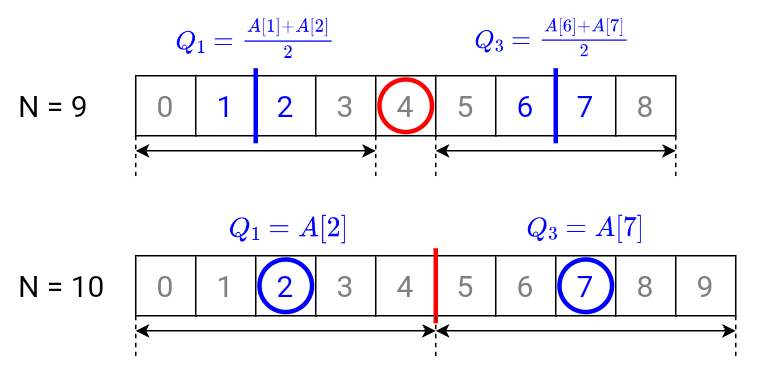
まずは、中央を境にデータを下位のデータと上位のデータに分けます。このとき、真ん中のデータが存在する場合(データが奇数個の場合)はそのデータを除外しますが、存在しない場合(データが偶数個の場合)はそのまま分けます。
そして、下位と上位それぞれのデータの中央値を$Q_2$と同様に求めると、下位のデータの中央値が第1四分位数$Q_1$、上位のデータの中央値が第3四分位数$Q_3$となります。
2. 四分位数の計算に必要なデータの位置を求める
1. で紹介した方法では、データの個数によって「1個のデータの値そのものが四分位数になる」場合と「隣り合う2個のデータの平均値が四分位数になる」場合があります。
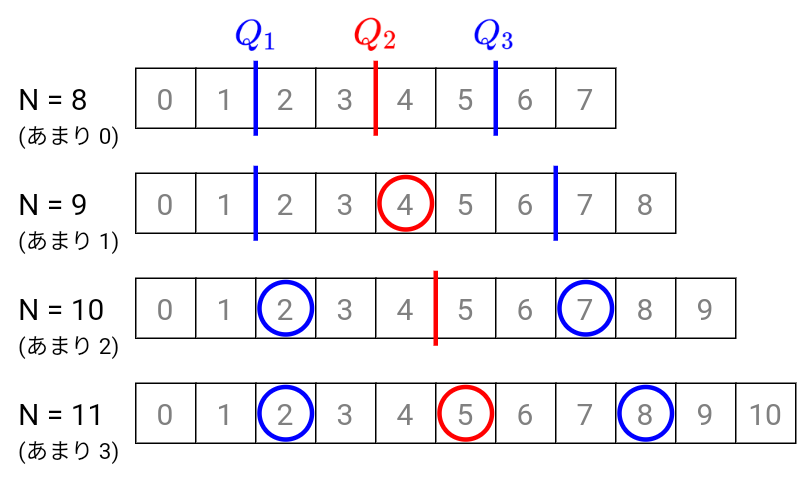
そのため、データの個数を$N$個とおくと、四分位数の求め方は$N$を$4$で割ったあまりによって$4$通りに場合分けされます。
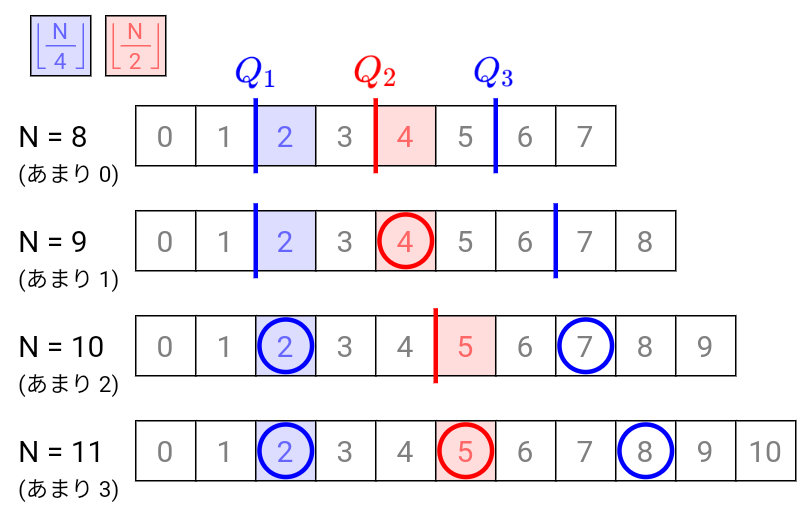
そこで、$\displaystyle\frac{N}{4},\frac{N}{2}$をそれぞれ小数点以下で切り捨てた値(以降は$\displaystyle\biggl\lfloor\frac{N}{4}\biggr\rfloor,\biggl\lfloor\frac{N}{2}\biggr\rfloor$で表します)を基準にして、それぞれの場合について四分位数の計算に必要なデータの位置を求めます。
第2四分位数(中央値)
$Q_2$は$\displaystyle\biggl\lfloor\frac{N}{2}\biggr\rfloor$の位置を基準にして求めます。
- $4$で割ったあまりが$0,2$のとき
$\displaystyle Q_2=\frac{A\bigl[\lfloor\frac{N}{2}\rfloor-1\bigr]+A\bigl[\lfloor\frac{N}{2}\rfloor\bigr]}{2}$ - $4$で割ったあまりが$1,3$のとき
$Q_2=A\bigl[\lfloor\frac{N}{2}\rfloor\bigr]$
第1四分位数
$Q_1$は$\displaystyle\biggl\lfloor\frac{N}{4}\biggr\rfloor$の位置を基準にして求めます。
- $4$で割ったあまりが$0,1$のとき
$\displaystyle Q_1=\frac{A\bigl[\lfloor\frac{N}{4}\rfloor-1\bigr]+A\bigl[\lfloor\frac{N}{4}\rfloor\bigr]}{2}$ - $4$で割ったあまりが$2,3$のとき
$Q_1=A\bigl[\lfloor\frac{N}{4}\rfloor\bigr]$
第3四分位数
$Q_3$は$Q_1$と左右対称な位置にあります。そこで、$Q_3$を求めるために必要なデータの位置は、データの末尾、つまり$(N-1)$番目のデータから$Q_1$で求めた分だけ戻った場所にあると考えます。
- $4$で割ったあまりが$0,1$のとき
$\displaystyle Q_1=\frac{A\bigl[(N-1)-(\lfloor\frac{N}{4}\rfloor-1\bigr)]+A\bigl[(N-1)-\lfloor\frac{N}{4}\rfloor\bigr]}{2}$
$\displaystyle\quad=\frac{A\bigl[N-\lfloor\frac{N}{4}\rfloor\bigr]+A\bigl[N-\lfloor\frac{N}{4}\rfloor-1\bigr]}{2}$ - $4$で割ったあまりが$2,3$のとき
$Q_1=A\bigl[(N-1)-\lfloor\frac{N}{4}\rfloor\bigr]=A\bigl[N-\lfloor\frac{N}{4}\rfloor-1\bigr]$
3. 関数を実装する
2. の場合分けをもとにして、四分位数を返す関数を実装します。せっかくなので、データの最小値と最大値も一緒に返すことにします。
#include <vector>
#include <algorithm>
//{最小値、第1四分位数、第2四分位数(中央値)、第3四分位数、最大値}をまとめた配列を返す
std::vector<double> quartile(std::vector<int> array)
{
int n = (int)array.size();
std::vector<double> q(5);
//データを小さい順にソート
sort(array.begin(), array.end());
//最小値と最大値
q[0] = (double)array[0], q[4] = (double)array[n - 1];
//四分位数
int n4 = n / 4, n2 = n / 2;
switch(n % 4)
{
case 0:
q[1] = (double)(array[n4 - 1] + array[n4]) / 2.0;
q[2] = (double)(array[n2 - 1] + array[n2]) / 2.0;
q[3] = (double)(array[n - n4 - 1] + array[n - n4]) / 2.0;
break;
case 1:
q[1] = (double)(array[n4 - 1] + array[n4]) / 2.0;
q[2] = (double)array[n2];
q[3] = (double)(array[n - n4 - 1] + array[n - n4]) / 2.0;
break;
case 2:
q[1] = (double)array[n4];
q[2] = (double)(array[n2 - 1] + array[n2]) / 2.0;
q[3] = (double)array[n - n4 - 1];
break;
case 3:
q[1] = (double)array[n4];
q[2] = (double)array[n2];
q[3] = (double)array[n - n4 - 1];
break;
}
return q;
}
動作確認
関数が正しく動くことを確認するために、$A[i]=i$を満たすデータについて四分位数を求めてみます。
//前略
#include <iostream>
using namespace std;
int main(void)
{
int n;
cin >> n;
vector<int> a(n);
for(int i = 0; i < n; ++i) a[i] = i;
vector<double> q = quartile(a);
for(int k = 0; k < 5; ++k) cout << q[k] << " ";
cout << endl;
return 0;
}
入力例1: 8
出力例1: 0 1.5 3.5 5.5 7
入力例2: 9
出力例2: 0 1.5 4 6.5 8
入力例3: 10
出力例3: 0 2 4.5 7 9
入力例4: 11
出力例4: 0 2 5 8 10
正しく四分位数を求めることができました。
4. 場合分けをせずに四分位数を求める
3. で四分位数を求める関数を作るという目標は一応達成しましたが、改めてコードを見返してみると、場合分けのせいでコードがごちゃごちゃしていてなんだかしっくり来ません。
そこで、場合分けをせずに四分位数を求められないか考えてみます。
四分位数の求め方を統一する
四分位数の求め方には「1個のデータの値が四分位数になる」場合と「隣り合う2個のデータの平均値が四分位数になる」場合の2通りがありましたが、これらは1通りにまとめることができます。
例えば、$N=9$個のデータにおいて中央値は$Q_2=A[4]$ですが、これは$\displaystyle A[4]=\frac{A[4]+A[4]}{2}$(同じ値のデータ2個の平均値)に書き換えることができます。つまり、前述の2通りの場合分けは、ともに 「2個のデータの平均値が四分位数になる」場合にまとめることができる わけです。
第2四分位数(中央値)
2. では以下のように場合分けしました。
- $4$で割ったあまりが$0,2$のとき($2$で割ったあまりが$0$のとき)
$\displaystyle Q_2=\frac{A\bigl[\lfloor\frac{N}{2}\rfloor-1\bigr]+A\bigl[\lfloor\frac{N}{2}\rfloor\bigr]}{2}$- $4$で割ったあまりが$1,3$のとき($2$で割ったあまりが$1$のとき)
$Q_2=A\bigl[\lfloor\frac{N}{2}\rfloor\bigr]$
これを$\displaystyle Q_2=\frac{A[i]+A[j]}{2}$の形でまとめて表せないか考えます。
まず、どちらの場合にも$A\bigl[\lfloor\frac{N}{2}\rfloor\bigr]$が登場しているので$\displaystyle j=\biggl\lfloor\frac{N}{2}\biggr\rfloor$でよいでしょう。
次に$i$について考えると、$2$で割ったあまりによって場合分けしていたので、こちらも$\displaystyle\biggl\lfloor\frac{N}{2}\biggr\rfloor$と似た形で表せそうです。そこで、仮に$\displaystyle i=\biggl\lfloor\frac{N-k}{2}\biggr\rfloor$とおいて$k$に当てはまる適切な整数を考えます。
2. の場合分けをもとに考えると、$i$の満たすべき条件は次のとおりです。
- $2$で割ったあまりが$0$のとき $\displaystyle\biggl\lfloor\frac{N-k}{2}\biggr\rfloor=\biggl\lfloor\frac{N}{2}\biggr\rfloor-1$
- $2$で割ったあまりが$1$のとき $\displaystyle\biggl\lfloor\frac{N-k}{2}\biggr\rfloor=\biggl\lfloor\frac{N}{2}\biggr\rfloor$
これを満たす$k$の値を考えると、$k=1$のときに条件を満たすことがわかります。よって、$\displaystyle i=\biggl\lfloor\frac{N-1}{2}\biggr\rfloor$と表せることがわかりました。
したがって、第2四分位数(中央値)は$\displaystyle Q_2=\frac{A\bigl[\lfloor\frac{N-1}{2}\rfloor\bigr]+A\bigl[\lfloor\frac{N}{2}\rfloor\bigr]}{2}$となります。
第1四分位数
2. では以下のように場合分けしました。
- $4$で割ったあまりが$0,1$のとき
$\displaystyle Q_1=\frac{A\bigl[\lfloor\frac{N}{4}\rfloor-1\bigr]+A\bigl[\lfloor\frac{N}{4}\rfloor\bigr]}{2}$- $4$で割ったあまりが$2,3$のとき
$Q_1=A\bigl[\lfloor\frac{N}{4}\rfloor\bigr]$
これも$Q_2$と同様に$\displaystyle Q_1=\frac{A[i]+A[j]}{2}$の形でまとめて表せないか考えます。
まず、どちらの場合にも$A\bigl[\lfloor\frac{N}{4}\rfloor\bigr]$が登場しているので$\displaystyle j=\biggl\lfloor\frac{N}{4}\biggr\rfloor$です。
次に$i$について考えると、$4$で割ったあまりによって場合分けしていたので、$Q_2$と同様に$\displaystyle i=\biggl\lfloor\frac{N-k}{4}\biggr\rfloor$とおいて$k$に当てはまる適切な整数を考えます。
2. の場合分けをもとに考えると、$i$の満たすべき条件は次のとおりです。
- $4$で割ったあまりが$0,1$のとき $\displaystyle\biggl\lfloor\frac{N-k}{4}\biggr\rfloor=\biggl\lfloor\frac{N}{4}\biggr\rfloor-1$
- $4$で割ったあまりが$2,3$のとき $\displaystyle\biggl\lfloor\frac{N-k}{4}\biggr\rfloor=\biggl\lfloor\frac{N}{4}\biggr\rfloor$
これを満たす$k$の値を考えると、$k=2$のときに条件を満たすことがわかります。よって、$\displaystyle i=\biggl\lfloor\frac{N-2}{4}\biggr\rfloor$と表せることがわかりました。
したがって、第1四分位数は$\displaystyle Q_1=\frac{A\bigl[\lfloor\frac{N-2}{4}\rfloor\bigr]+A\bigl[\lfloor\frac{N}{4}\rfloor\bigr]}{2}$となります。
第3四分位数
$Q_3$は$Q_1$と左右対称な位置にあるので、2. と同様に$(N-1)$番目のデータから$Q_1$で求めた分だけ戻った場所にあると考えます。
したがって、第3四分位数は$\displaystyle Q_3=\frac{A\bigl[(N-1)-\lfloor\frac{N-2}{4}\rfloor\bigr]+A\bigl[(N-1)-\lfloor\frac{N}{4}\rfloor\bigr]}{2}$$\displaystyle=\frac{A\bigl[\lfloor\frac{3N+1}{4}\rfloor\bigr]+A\bigl[\lfloor\frac{3N-1}{4}\rfloor\bigr]}{2}$となります。
本題からそれるので計算過程は割愛しますが、切り捨てと整数の計算については以下の記事で紹介しています。
5. 関数を実装する(改良版)
4. の結果をもとに関数を実装します。
- 第1四分位数
$\displaystyle Q_1=\frac{A\bigl[\lfloor\frac{N-2}{4}\rfloor\bigr]+A\bigl[\lfloor\frac{N}{4}\rfloor\bigr]}{2}$ - 第2四分位数(中央値)
$\displaystyle Q_2=\frac{A\bigl[\lfloor\frac{N-1}{2}\rfloor\bigr]+A\bigl[\lfloor\frac{N}{2}\rfloor\bigr]}{2}$ - 第3四分位数
$\displaystyle Q_3=\frac{A\bigl[\lfloor\frac{3N-1}{4}\rfloor\bigr]+A\bigl[\lfloor\frac{3N+1}{4}\rfloor\bigr]}{2}$
#include <vector>
#include <algorithm>
//{最小値、第1四分位数、第2四分位数(中央値)、第3四分位数、最大値}をまとめた配列を返す
std::vector<double> quartile(std::vector<int> array)
{
int n = (int)array.size();
std::vector<double> q(5);
sort(array.begin(), array.end());
q[0] = (double)array[0];
q[1] = (double)(array[(n - 2) / 4] + array[n / 4]) / 2.0;
q[2] = (double)(array[(n - 1) / 2] + array[n / 2]) / 2.0;
q[3] = (double)(array[(3 * n - 1) / 4] + array[(3 * n + 1) / 4]) / 2.0;
q[4] = (double)array[n - 1];
return q;
}
かなりシンプルに実装できました。
おわりに
色々と考える必要があってすこし大変でしたが、関数を作ってみるのは結構面白かったです。おおまかなデータの分布を手早く調べたいときにこの関数が役に立つと思います。