はじめに
競プロでは、整数同士を割り算した値を小数点以下で切り捨て・切り上げた値を使うときがよくあります。
そこで、ふと「切り捨て・切り上げを使った計算をしたいときや、切り捨てと切り上げを変換したいときに使える公式みたいなのがあればいいな」と思い、考えたことを書いてみました。
1. 切り捨て・切り上げ とは
切り捨て・切り上げについて知らない人はいないと思いますが、一応確認しておきます。
「$x$の小数点以下を切り捨てる」とは、「$x$以下の最大の整数 を求める」ことです。例えば$2.9$を小数点以下で切り捨てると$2$、$-1.4$を小数点以下で切り捨てると$-2$になります。
一方、「$x$の小数点以下を切り上げる」とは、「$x$以上の最小の整数 を求める」ことです。例えば$2.9$を小数点以下で切り上げると$3$、$-1.4$を小数点以下で切り上げると$-1$になります。
数学では、「$x$以下の最大の整数」のことを$\lfloor x\rfloor$で表し、これを 床関数 と呼びます。一方、「$x$以上の最小の整数」のことを$\lceil x\rceil$で表し、これを 天井関数 と呼びます。
$\lfloor x\rfloor$は小さい横棒 - が縦棒の下についているので床関数(=切り捨て)、$\lceil x\rceil$は上についているので天井関数(=切り上げ)です。分かりやすいですね。この記号は便利なので、以降は切り捨てを$\lfloor x\rfloor$、切り上げを$\lceil x\rceil$で表すことにします。
2. 公式を考えてみる
競プロで一番よく使うのは整数同士の割り算の切り捨てです。そこで、整数$N$を自然数$d$で割った値$\displaystyle\frac{N}{d}$の切り捨て・切り上げについて考えてみます。
公式①
-\lfloor x\rfloor=\lceil -x\rceil
これは整数同士の割り算に限らず実数全体に言える話ですが、実数を切り捨てた値にマイナスをつけたものは、マイナスをつけて切り上げた値に等しいです。
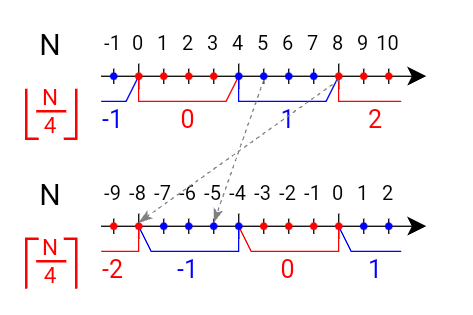
数直線で考えてみると、$0$を中心として数直線の左右をひっくり返す($+$と$-$を逆にする)ことで、切り捨てが切り上げに変わります。(図は$d=4$の場合を示しています)
公式②
\biggl\lfloor\frac{N\pm Ad}{d}\biggr\rfloor=\biggl\lfloor\frac{N}{d}\pm A\biggr\rfloor=\biggl\lfloor\frac{N}{d}\biggr\rfloor\pm A
$N$に$d$の倍数$Ad$を足し引きしてから$d$で割って切り捨てた値、つまり$\displaystyle\frac{N}{d}$に$A$を足し引きしてから切り捨てた値は、切り捨ててから$A$を足し引きした値に等しいです。
下の図では、$N$に$d$を足したとき($A=1$のとき)の変化を示しています。
これは切り上げの場合も同じです。
\biggl\lceil\frac{N\pm Ad}{d}\biggr\rceil=\biggl\lceil\frac{N}{d}\pm A\biggr\rceil=\biggl\lceil\frac{N}{d}\biggr\rceil\pm A
公式③
\biggl\lceil\frac{N}{d}\biggr\rceil=\biggl\lfloor\frac{N+d-1}{d}\biggr\rfloor\biggl(=\biggl\lfloor\frac{N-1}{d}\biggr\rfloor+1\biggr)
これは競プロ界では有名(?)な、切り上げを切り捨てで表す公式ですね。説明は面倒なので割愛しますが、図を見れば$+\ d-1$の意味がなんとなく分かると思います。
なお、この公式を変形すると切り捨てを切り上げで表すこともできます。この式は後で使うので 公式③' としておきます。
\biggl\lfloor\frac{N}{d}\biggr\rfloor=\biggl\lceil\frac{N-d+1}{d}\biggr\rceil\biggl(=\biggl\lceil\frac{N+1}{d}\biggr\rceil-1\biggr)
3. 切り捨て・切り上げをプログラムに実装する
C++では、整数$N$を自然数$d$で割った N / d を計算した値は、$N\ge 0$のとき$\displaystyle\biggl\lfloor\frac{N}{d}\biggr\rfloor$(切り捨て)、$N\lt 0$のとき$\displaystyle\biggl\lceil\frac{N}{d}\biggr\rceil$(切り上げ)になります。
言い換えると、$N$が$d$の倍数でないときの N / d の値は、数直線上での$\displaystyle\frac{N}{d}$の両隣の整数のうち$0$に近いほうの値になります。
そこで、$\displaystyle\biggl\lfloor\frac{N}{d}\biggr\rfloor$および$\displaystyle\biggl\lceil\frac{N}{d}\biggr\rceil$をプログラムに実装するには、$N$の正負による場合分けが必要です。公式③ および 公式③' を使うことで、これを実装することができます。
切り捨て(床関数)
- $N\ge 0$のとき
そのまま N / d を計算すればよいです。
- $N\lt 0$のとき
公式③' より (N - d + 1) / d を計算すればよいです。
$N\lt 0$かつ$d\gt 0$なので$N-d+1<0$ですから、(N - d + 1) / d $\displaystyle=\biggl\lceil\frac{N-d+1}{d}\biggr\rceil=\biggl\lfloor\frac{N}{d}\biggr\rfloor$となります。
なお、関数に実装する際は$d\lt 0$の場合もあり得るので、その場合はあらかじめ$N$および$d$の符号を反対にする必要があります。
また、(N - d + 1) / d をそのまま計算するとオーバーフローする可能性があるので、代わりに 公式② を使って式変形した (N + 1) / d - 1 を使います。
//切り捨て
int floor(int N, int d)
{
if(d < 0)
N *= -1, d *= -1;
if(N < 0)
return (N + 1) / d - 1;
else
return N / d;
}
切り上げ(天井関数)
- $N\ge 0$のとき
公式③ より (N + d - 1) / d を計算すればよいです。
$N\ge 0$かつ$d\gt 0$なので$N+d-1\ge 0$ですから、(N + d - 1) / d $\displaystyle=\biggl\lfloor\frac{N+d-1}{d}\biggr\rfloor=\biggl\lceil\frac{N}{d}\biggr\rceil$となります。
- $N\lt 0$のとき
そのまま N / d を計算すればよいです。
こちらも同様に、オーバーフローを防ぐために (N + d - 1) / d を式変形した (N - 1) / d + 1 を使います。ただしこの式だと$N=0$のときだけ$N-1\lt 0$となってしまうため、条件式を$N\ge 0$から$N\gt 0$に変える必要があります。
//切り上げ
int ceil(int N, int d)
{
if(d < 0)
N *= -1, d *= -1;
if(N > 0)
return (N - 1) / d + 1;
else
return N / d;
}
4. 公式を使った計算
公式①〜③を使うことで、切り捨て・切り上げと整数の足し算・引き算もできるようになります。(複数の切り捨て・切り上げが出てくる式の計算はできませんが…)
試しに、次の問題を公式を使って解いてみましょう。
$\displaystyle(N-1)-\biggl\lfloor\frac{N-2}{4}\biggr\rfloor$ を計算して、$\displaystyle\biggl\lfloor\frac{(Nの一次式)}{4}\biggr\rfloor$ の形で表せ。
まずは 公式② を使いたくなりますが、$\displaystyle(N-1)-\biggl\lfloor\frac{N-2}{4}\biggr\rfloor=\biggl\lfloor(N-1)-\frac{N-2}{4}\biggr\rfloor$としてはいけません。なぜなら、公式② は切り捨て・切り上げの前が$+$のときにしか使えないからです。
そこで、最初は 公式① を使って切り捨ての前の$-$を$+$に変えます。このとき切り捨ては切り上げに変わります。
(N-1)-\biggl\lfloor\frac{N-2}{4}\biggr\rfloor=(N-1)+\biggl\lceil-\frac{N-2}{4}\biggr\rceil
次に 公式② を使って$(N-1)$を切り上げの中に入れて計算します。
\begin{align}
&(N-1)+\biggl\lceil-\frac{N-2}{4}\biggr\rceil \\
=&\biggl\lceil(N-1)-\frac{N-2}{4}\biggr\rceil \\
=&\biggl\lceil\frac{4(N-1)-(N-2)}{4}\biggr\rceil \\
=&\biggl\lceil\frac{4N-4-N+2}{4}\biggr\rceil \\
=&\biggl\lceil\frac{3N-2}{4}\biggr\rceil
\end{align}
最後に 公式③ を使って切り上げを切り捨てに変換します。
\begin{align}
&\biggl\lceil\frac{3N-2}{4}\biggr\rceil \\
=&\biggl\lfloor\frac{(3N-2)+4-1}{4}\biggr\rfloor \\
=&\biggl\lfloor\frac{3N+1}{4}\biggr\rfloor
\end{align}
したがって、$\displaystyle(N-1)-\biggl\lfloor\frac{N-2}{4}\biggr\rfloor$を計算した答えは$\displaystyle\biggl\lfloor\frac{3N+1}{4}\biggr\rfloor$となります。
計算が正しいか確認するために、先程実装した関数を使ってコードを書いてみましょう。
コード
#include <iostream>
using namespace std;
//切り捨て
int floor(int N, int d)
{
if(d < 0)
N *= -1, d *= -1;
if(N < 0)
return (N + 1) / d - 1;
else
return N / d;
}
int main(void)
{
for(int N = -10; N <= 10; ++N)
{
cout << (N - 1) - floor(N - 2, 4) << " ";
}
cout << "\n";
for(int N = -10; N <= 10; ++N)
{
cout << floor(3 * N + 1, 4) << " ";
}
cout << "\n";
return 0;
}
標準出力
-8 -7 -6 -5 -5 -4 -3 -2 -2 -1 0 1 1 2 3 4 4 5 6 7 7
-8 -7 -6 -5 -5 -4 -3 -2 -2 -1 0 1 1 2 3 4 4 5 6 7 7
ちゃんと同じ値になっていますね。
おわりに
このように、公式を使うことで切り捨て・切り上げをプログラムに実装したり、切り捨て・切り上げと整数の足し算・引き算をしたりできます。これらの公式を使う場面はあまりないかもしれませんが、頭の片隅にでも置いておくとどこかで役立つかもしれません。