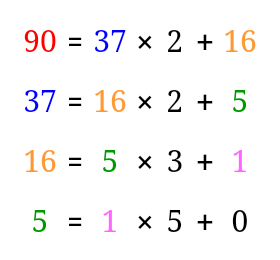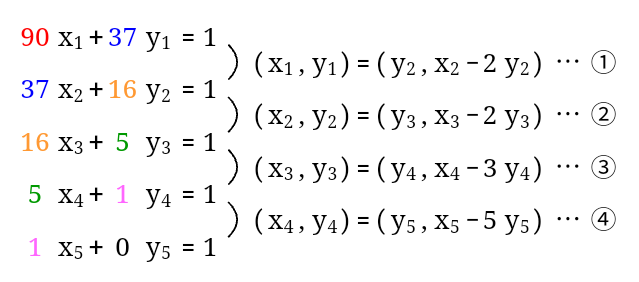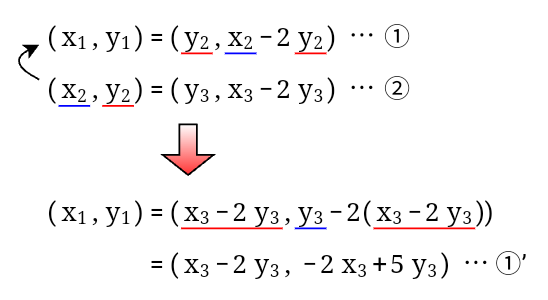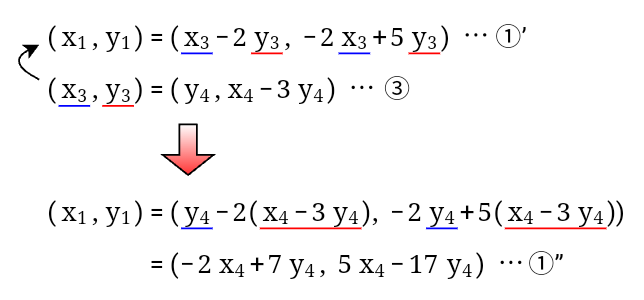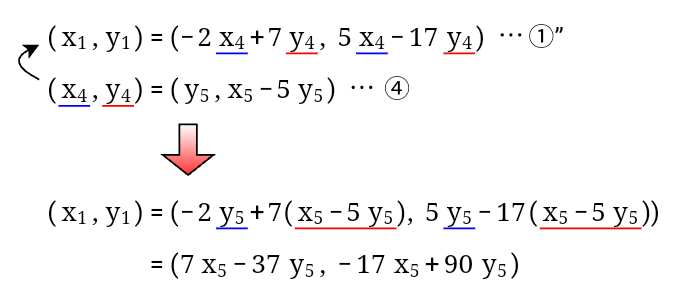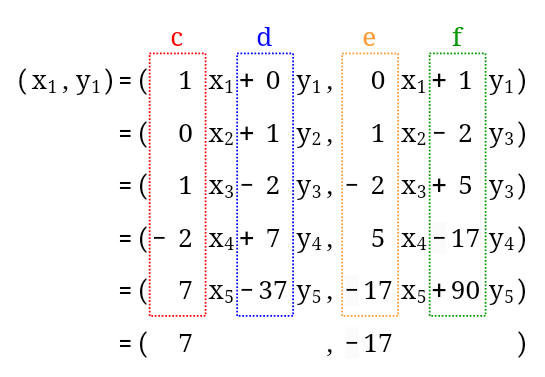Go to Qiita Advent Calendar 2024 Top
LoginSignup
4
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@luuguas

拡張ユークリッドの互除法を実装しよう

Last updated at Posted at 2023-08-29

はじめに

この記事は、主に競技プログラミングをする人に向けて、拡張ユークリッドの互除法の仕組みおよび、拡張ユークリッドの互除法を実装する際の考え方をまとめたものです。

拡張ユークリッドの互除法は競技プログラミングのとある場面で使われるテクニックですが、いざそれを自分で実装しようとすると複雑さゆえに苦戦する人もいるのではないかと思います。(というか私自身がかなり手こずりました)

そこでこの記事では、そんな人でも理解しやすいように、アルゴリズムがどのように動いているか、どうすればうまくプログラムに実装できるかを丁寧に解説しました。
この記事が皆さんの理解の助けになれば幸いです。

目次

はじめに
　目次

1. ユークリッドの互除法
　1-1. 原理
　1-2. 再帰関数による実装
　1-3. 非再帰関数による実装

2. 拡張ユークリッドの互除法
　2-1. 一次不定方程式
　2-2. 拡張ユークリッドの互除法を使った特殊解の求め方
　2-3. 再帰関数による実装
　2-4. 非再帰関数による実装

3. 拡張ユークリッドの互除法の別解法
　3-1. 原理
　3-2. 非再帰関数による実装

4. 拡張ユークリッドの互除法の応用 - mod p における逆元

おわりに
　参考

1. ユークリッドの互除法

本題に入る前に、まずは拡張ユークリッドの互除法の考え方のもととなる、ユークリッドの互除法について解説します。

ユークリッドの互除法を既に理解している方は、この章を読み飛ばしてもらってもかまいません。

1-1. 原理

ユークリッドの互除法は、2つの自然数の 最大公約数 を求めるための有名なアルゴリズムです。
このアルゴリズムでは、次の定理を使うことで、最大公約数を高速に求めることができます。

2つの自然数$a,b$について、$a$を$b$で割ったあまりを$r$とすると、「$a$と$b$の最大公約数」は「$b$と$r$の最大公約数」に等しい。

試しに、ユークリッドの互除法を使って最大公約数を求めてみましょう。

例題1: $513$と$399$の最大公約数を求めよ。

まず、$513$を$399$で割ったあまりを求めます。
$513=399\times 1+114$なので、あまりは$114$です。
すると、上記の性質より 「$513$と$399$の最大公約数」は「$319$と$114$の最大公約数」に等しい と分かります。

まだ数が大きいので、「$319$と$114$の最大公約数」について、もう一度同じことをします。
$319=114\times 2+57$なので、$319$を$114$で割ったあまりは$57$です。
よって「$319$と$114$の最大公約数」は「$114$と$57$の最大公約数」に等しいです。

さらにもう一度同じことをすると、$114=57\times 2+0$なので、$114$はちょうど$57$の倍数です。
したがって、「$114$と$57$の最大公約数」は$57$と分かりました。

最後に、今までした計算を逆にたどります。
$57$ =「$114$と$57$の最大公約数」=「$399$と$114$の最大公約数」=「$513$と$399$の最大公約数」 なので、$513$と$399$の最大公約数は$57$であると分かり、答えを求めることができました。

このように、$a$が$b$の倍数となるまで計算を繰り返すことで、大きな数であっても少ない計算量で最大公約数を求めることができます。

Euclid_1.drawio.png

ところで、例題1 では2つの自然数$a,b$が$a\ge b$である場合を考えましたが、$a\lt b$である場合はどうなるのでしょうか。

試しに、例題1 の$a,b$の値を入れ替えて、$a=399,b=513$について考えてみます。
$399=513\times 0+399$なので、あまりは$r=399$です。
すると、上記の性質より「『$399$と$513$の最大公約数』は『$513$と$399$の最大公約数』に等しい」となり、値が元に戻りました。

このように、$a\lt b$である場合は、1回計算をすることで$a,b$の値がそのまま入れ替わって$a\ge b$となります。
したがって、ユークリッドの互除法は$a,b$の大小関係にかかわらず使うことができます。

1-2. 再帰関数による実装

では、2つの自然数 a, b の最大公約数を返す関数 gcd(a, b)1 を、ユークリッドの互除法を使って実装してみましょう。

例題1 では、以下の考え方を繰り返し使うことで最大公約数を求めました。

「$a$と$b$の最大公約数」について、

  • $a$が$b$の倍数、つまり$r=0$ならば、最大公約数は$b$である
  • $r\neq 0$ならば、最大公約数は「$b$と$r$の最大公約数」に等しい

これをプログラムの処理に置き換えてみると、次のようになります。
3行目を再帰関数を使った処理に置き換えるところがポイントです。

gcd(a, b) は、

  • $r=0$ならば、$b$の値を返す
  • $r\neq 0$ならば、gcd(b, a % b) を呼び出して、その返り値を返す

(a % b は$a$を$b$で割ったあまり$r$を表します)

ただし、ユークリッドの互除法をプログラムに実装するときは、条件を単純化するために$r=0$の代わりに$b=0$を使うことが多いです2。(もちろん$r=0$を使ってもかまいません)

$b=0$を条件としてよい理由は、例題1 で考えてみるとすぐに分かります。
gcd(114, 57) が呼び出されたときに、あえて$b$の値を返さずに gcd(b, a % b) を呼び出すと、$r=0$なので、呼び出されるのは gcd(57, 0) です。
すると、これが$b=0$の条件にあてはまり、このときの$a$の値が求める最大公約数となります。

条件を$b=0$に直した上で、もう一度関数の処理を考えてみると、次のようになります。

gcd(a, b) は、

  • $b=0$ならば、$a$の値を返す
  • $b\neq 0$ならば、gcd(b, a % b) を呼び出して、その返り値を返す

あとは、これをそのままコードにすれば完成です。

コード例

C++

long long gcd(long long a, long long b) {
    if (b == 0)
        return a;
    else
        return gcd(b, a % b);
}

Python

def gcd(a, b):
    if b == 0:
        return a
    else:
        return gcd(b, a % b)

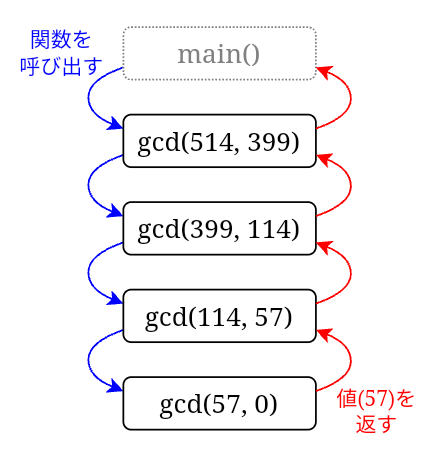
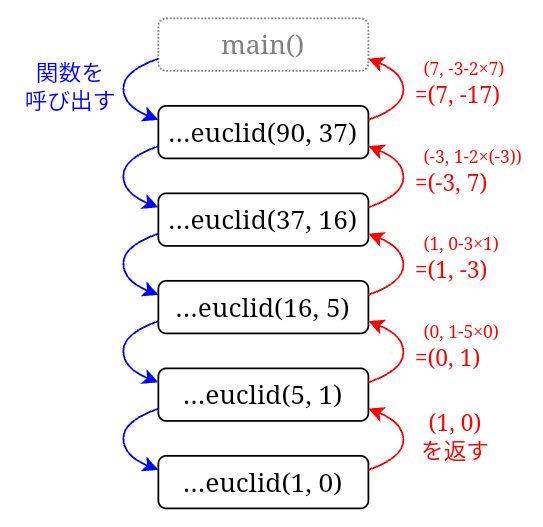
例題1 をこの関数を使って解くときの関数の動作は、以下の図のようになります。
まず、関数の呼び出しが繰り返しおこなわれます(青矢印)。
そして、gcd(57, 0) で最大公約数が求まると、呼び出し元にその値が順々に返されます(赤矢印)。

Euclid_2.drawio.png

1-3. 非再帰関数による実装

1-2. では、gcd(a, b) を関数内で関数自身を呼び出す再帰関数として実装しました。
再帰関数は便利ですが、関数の動きが直感的に理解しづらいという人もいるかと思います。
そこで、この節では再帰関数を使わずに実装する方法を解説します。

といっても、具体的には「gcd(b, a % b) を呼び出す」という処理を 「変数$a$に$b$を、変数$b$に$r$を代入する」 という処理に置き換えるだけです。
1-2. で書いた処理をこれに置き換えると、次のようになります。

手順1: $b$の値を調べる。
手順2: $b=0$ならば、$a$の値を返す。
手順3: $b\neq 0$ならば、変数$a$に$b$を、変数$b$に$r$を代入して、手順1に戻る。

これを実装しましょう。
「$b=0$になるまで計算を繰り返す」、つまり「$b\neq 0$である限り計算を繰り返す」という処理は、while文を使うことで簡単に実装できます。

コード例

C++

C++では、変数$r$を用意して a % b を一旦代入しておき、それから変数$a$に$b$を、変数$b$に$r$を代入します。

long long gcd(long long a, long long b) {
    long long r;
    while (b != 0) {
        r = a % b;
        a = b;
        b = r;
    }
    return a;
}

Python

Pythonでは、複数の変数に異なる値を同時に代入できるので、変数$r$を使わずに実装できます。

def gcd(a, b):
    while b != 0:
        a, b = b, a % b
    return a

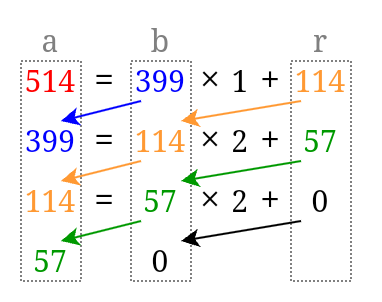
例題1 をこの関数を使って解くときの関数の動作は、以下の図のようになります。
矢印が変数への代入を表します。

Euclid_3.drawio.png

2. 拡張ユークリッドの互除法

ユークリッドの互除法の説明が終わったので、いよいよ本題である拡張ユークリッドの互除法について解説します。

2-1. 一次不定方程式

拡張ユークリッドの互除法は、一次不定方程式 の解を求めるためのアルゴリズムです。

一次不定方程式とは

まずは、一次不定方程式がどのようなものなのかを理解するために、具体例を見てみましょう。

例題2: $3x+5y=1$を満たす整数$(x,y)$の組を1つ求めよ。

一次不定方程式とは、$ax+by=c$ ($a,b,c$は整数) の形で表される方程式のことです。
そして、方程式を満たす整数3の組$(x,y)$を求めることを「一次不定方程式を解く」といい、求めた整数の組$(x,y)$のことを「一次不定方程式の(整数)解」といいます。

では、例題2 の答え、つまり一次不定方程式$3x+5y=1$の整数解の1つを求めてみましょう。

この例では数が小さいので、$x,y$に色々な値を代入してみるだけで解が求められそうです。
試しにやってみると、$x=2,y=-1$のときに (左辺)$=3\times 2+5\times(-1)=6-5=1$ となり、等式が成り立ちます。
したがって、この方程式の解の1つは$(x,y)=(2,-1)$です。

特殊解と一般解

わざわざ「解の1つ」と書いたのでお分かりかと思いますが、例題2 の答えは$(x,y)=(2,-1)$以外にも存在します。
例えば、$(x,y)=(7,-4),(-3,2)$は、どちらもこの方程式の解です。

実は、一次不定方程式の整数解は(1つ解が見つかったならば)無数に存在することが分かっています。
そして、それらの無数の解は、1つの式でまとめて表すことができます。

例えば 例題2 では、方程式のすべての整数解を、整数$k$を使って$(x,y)=(-5k+2,3k-1)$と表すことができます。
試しに、この式に$k=0,1,-1$をそれぞれ代入してみると、順に$(x,y)=(2,-1),(7,-4),(-3,2)$となり、どれも方程式の解となることが分かります。

一次不定方程式において、$(x,y)=(2,-1)$のような具体的な1つの解のことを 特殊解 といいます。
一方、$(x,y)=(-5k+2,3k-1)$のように無数の解を1つの式で表したもののことを 一般解 と言います。

そして、特殊解を1つ求めることができれば、それを使って一般解を表すことができます。
具体的には、$ax+by=c$の特殊解の1つを$(x,y)=(X,Y)$とすると、一般解は整数$k$を用いて$(x,y)=(-bk+X,ak+Y)$と表されます。

少し長くなりましたが、要するに一次不定方程式で重要なのは、どのようにして特殊解を求めるか ということです。
例題2 では$x,y$に色々な値を代入して当てずっぽうで特殊解を求めましたが、数が大きい場合はそう簡単には求められません。
この特殊解を数学的にきちんと求めるためのアルゴリズムが、拡張ユークリッドの互除法です。

一次不定方程式には、整数解が存在しない場合もあります。

  • $c$が$\gcd (a,b)$の倍数であるならば、解は無数に存在する。
  • そうでないならば、解は存在しない。

証明はここでは割愛しますが、一般解の導出方法なども含めて詳しく知りたいという人は、以下のサイトを読んでみてください。

2-2. 拡張ユークリッドの互除法を使った特殊解の求め方

では、一次不定方程式の特殊解を拡張ユークリッドの互除法を使って求める方法を、次の例題を使って解説します。

例題3: $90x+37y=4$を満たす整数$(x,y)$の組を1つ求めよ。

まずは、$90$と$37$の最大公約数を求めるときのユークリッドの互除法の計算をそのままおこないます。

ExtendedEuclid_1.drawio.png

次に、式の形を$a=bq+r$から$r=a-bq$に移項します。($q$は$a$を$b$で割った商を表します)
なお、最終行は以降の計算で使わないので省きます。
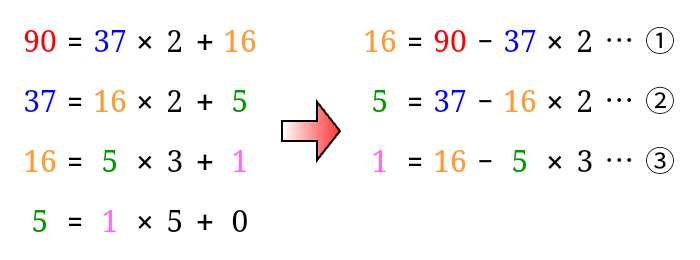
そして、変形した式に上から順に①〜③の番号をつけます。

ExtendedEuclid_2.drawio.png

そして、互除法の計算を逆にたどるようにして、③に②,①を順に代入していきます。

  • ②の左辺は$5$なので、③の右辺の$5$に②を代入して、$5$を消去します。
    そして、式の形が$1=37x+16y$となるように式を整理します。(整理したあとの式を③’とします)

ExtendedEuclid_3.drawio.png

  • ①の左辺は$16$なので、③’の右辺の$16$に①を代入して、$16$を消去します。
    そして、式の形が$1=90x+37y$となるように式を整理します。

ExtendedEuclid_4.drawio.png

すると、$90\times 7+37\times(-17)=1$という式が得られました。
例題3 の右辺は$4$なので、最後にこの式の両辺を$4$倍すると、$90\times(7\times 4)+37\times(-17\times 4)=4$、つまり$90\times 28+37\times(-68)=4$となります。
したがって、この式と元の方程式を比較して、解は$(x,y)=(28,-68)$と求まりました。

このような計算をおこなうことで、一次不定方程式の特殊解を求めることができます。

2-3. 再帰関数による実装

では、一次不定方程式$ax+by=\gcd(a,b)$の特殊解$(x,y)$を返す関数 extended_euclid(a, b) を、拡張ユークリッドの互除法を使って実装してみましょう。

ここからは、$ax+by=1$($a,b$は互いに素4) の場合だけを考えることにします。

なぜなら、$\gcd(a,b)\gt 1$の場合は両辺を$\gcd(a,b)$で割ることで、特殊解$(x,y)$を変えずに$a^\prime x+b^\prime y=1$の形にすることができるからです。
また、右辺が$1$でない場合も 例題3 と同様に特殊解を整数倍すればよいので、これも無視します。

互除法の計算を関係式で表す

拡張ユークリッドの互除法の計算は少し複雑ですが、分かりやすく言い換えると、次の計算を繰り返していることが分かります。

  • $bx^\prime+ry^\prime=1$の特殊解$(x^\prime,y^\prime)$が求まったら、方程式に$r=a-bq$を代入して、$ax+by=1$の特殊解$(x,y)$を求める

例題3 の場合で考えてみましょう。

まず、③を書き換えると$16\times 1+5\times(-3)=1$となるので、$16x^\prime+5y^\prime=1$の特殊解は$(x^\prime,y^\prime)=(1,-3)$と分かります。
すると、この式に$5=37-16\times 2$ …② を代入して整理することで$37\times(-3)+16\times 7=1$となり、$37x+16y=1$の特殊解が$(x,y)=(-3,7)$と求まります。

次の計算でも、$37x^\prime+16y^\prime=1$の特殊解が$(x^\prime,y^\prime)=(-3,7)$と分かっているので、この式に$16=90-37\times 2$ …① を代入して整理することで、$90x+37y=1$の特殊解が$(x,y)=(7,-17)$と求まります。

この計算を一般化して、特殊解$(x,y)$を$x^\prime,y^\prime$を使った式で表してみましょう。

  • $bx^\prime+ry^\prime=1$に$r=a-bq$を代入すると、$bx^\prime+(a-bq)\times y^\prime=1$
    式を整理すると、$bx^\prime+ay^\prime-bqy^\prime=1\Leftrightarrow ay^\prime+b(x^\prime-qy^\prime)=1$

したがって、$(x,y)=(y^\prime,x^\prime-qy^\prime)$という関係式が求まりました。

条件分岐と特殊解を考える

前項で関係式は求まったので、次は条件分岐について考えます。
1-2. では$b=0$を条件にしたので、今回もそれに合わせましょう。

これも 例題3 の場合で考えてみます。
例題3 では、③の時点で既に$16x+5y=1$の特殊解が求まりますが、あえて$b=0$となるまで計算を進めてみましょう。

すると、$16x+5y=1$の特殊解を求めるには$5x+1y=1$の特殊解が必要で、$5x+1y=1$の特殊解を求めるには$1x+0y=1$の特殊解が必要… となり、$b=0$のときの方程式の形は必ず$1\times x+0\times y=1$になります。
したがって、この式を満たす$(x,y)$を考えると、$b=0$のときの特殊解は$(x,y)=(1,0)$5とすればよいことが分かりました。

係数が負のときの特殊解を考える

例題3 では、$x,y$の係数がともに正の場合を考えました。
ですが、$90x-37y=1$のように、係数のいずれか、または両方が負の場合の特殊解を求めたい場合もあります。
このときは注意が必要です。

プログラミング言語における$a\div b$の商と余りは、数学におけるそれとは異なります。(さらに、C++とPythonでも挙動が異なります)
よって、例えば$90x-37y=1$の特殊解を求めようとして直接 extended_euclid(90, -37) を呼び出すと、正しい特殊解を得られない可能性があります。
そのため、係数が負の場合は符号を正に変えてから関数を呼び出し、関数の外側で特殊解の正負を逆にする とよいです。

例えば、$90x-37y=1$の特殊解を求めるには、まず$90x+37y=1$の特殊解を extended_euclid(90, 37) で求めます。
すると、$(x,y)=(7,-17)$が得られるので、$y$の正負を逆にすれば、$90x-37y=1$の特殊解が$(x,y)=(7,17)$と求まります。

実装

以上から、1-2. と同様に再帰関数を使った処理を考えると、関数の処理は次のようになります。

extended_euclid(a, b) ($a,b$は非負整数) は、

  • $b=0$ならば、$(1,0)$を返す
  • $b\neq 0$ならば、extended_euclid(b, a % b) を呼び出し、その返り値を変数$(x^\prime, y^\prime)$に代入したうえで、$(y^\prime,x^\prime-qy^\prime)$を返す

なお、拡張ユークリッドの互除法は、ユークリッドの互除法と同様に$a\lt b$のときも正しく動作します。
$a\lt b$のときは、$a$を$b$で割った商は$q=0$、あまりは$r=a$です。
よって、呼び出す関数は extended_euclid(b, a) となり、さらに$(x,y)=(y^\prime,x^\prime-0\times y^\prime)=(y^\prime,x^\prime)$なので、$a,b$の値が入れ替わると同時に$x,y$の値も入れ替わります。

コード例

C++

C++では、2つの値の組を返すには構造体や pair を使う必要がありますが、わざわざ新しい要素を追加するのは面倒なので、変数$x,y$を参照渡しする方法を使うことにします。(あまり良くない方法ですが)
関数の引数に変数$x,y$を渡して関数を呼び出すと、変数$x,y$に解が代入されます。

void extended_euclid(long long a, long long b, long long& x, long long& y) {
    if(b == 0) {
        x = 1;
        y = 0;
    }
    else {
        long long xd, yd; //x', y'
        extended_euclid(b, a % b, xd, yd);
        x = yd;
        y = xd - a / b * yd;
    }
}

なお、処理を少し工夫すると、変数$x^\prime,y^\prime$を使わずに実装することができます。
extended_euclid(b, a % b, xd, yd) の代わりに extended_euclid(b, a % b, y, x) を呼び出すと、変数$x,y$にはそれぞれ$y^\prime,x^\prime$が代入されます。
したがって、さらに変数$y$の値を$qx(=qy^\prime)$だけ減らせば、$(x,y)=(y^\prime,x^\prime-qy^\prime)$となります。

void extended_euclid(long long a, long long b, long long& x, long long& y) {
    if(b == 0) {
        x = 1;
        y = 0;
    }
    else {
        extended_euclid(b, a % b, y, x);
        y -= a / b * x;
    }
}

Python

Pythonでは、タプルを使って解を返すことができます。

def extended_euclid(a, b):
    if b == 0:
        return (1, 0)
    else:
        xd, yd = extended_euclid(b, a % b)
        return (yd, xd - a // b * yd)

例題3 の$90x+37y=1$をこの関数を使って解くときの関数の動作は、以下の図のようになります。(関数名が長いので少し省略しています)

ExtendedEuclid_5.drawio.png

2-4. 非再帰関数による実装

拡張ユークリッドの互除法についても、再帰関数を使わずに実装する方法について解説します。

関係式を活用して特殊解を求める

2-3. では互除法の計算を逆にたどって特殊解を求めましたが、今回は計算の順序通りに特殊解を求める方法について考えます。
これも例題3を使って考えましょう。

まずは、$90x_1+37y_1=1,\ 37x_2+16y_2=1,\ \cdots,\ 1x_5+0y_5=1$のように、特殊解に順に番号をつけます。
すると、2-3. で求めた関係式を使って、隣り合う番号の特殊解同士の関係式を作ることができます。
これらの式に①〜④の番号をつけておきます。

ExtendedEuclid_6.drawio.png

そして、①に②,③,④をこの順に代入していきます。

  • ①の右辺の$x_2,y_2$に②を代入して、式を整理します。(代入した後の式を①’とします)

ExtendedEuclid_7.drawio.png

  • 同様にして、①’に③を代入して整理し、さらに④を代入して整理します。

ExtendedEuclid_8.drawio.png
ExtendedEuclid_9.drawio.png

すると、$(x_1,y_1)$を$x_5,y_5$を使った式で表すことができました。
最後に$(x_5,y_5)=(1,0)$を代入すれば、特殊解が$(x_1,y_1)=(7,-17)$と求まります。

処理を一般化する

上記の計算では、次の処理を繰り返しおこないました。

  • $(x_1,y_1)$と$(x_k,y_k)$の関係式が求まったら、$(x_k,y_k)$と$(x_{k+1},y_{k+1})$の関係式を代入して、$(x_1,y_1)$と$(x_{k+1},y_{k+1})$の関係式を求める

上記の計算からも分かるように、$(x_1,y_1)$と$(x_k,y_k)$の関係式は$x_k,y_k$に関する一次式となります。
ですから、関係式における$x_k,y_k$の係数を変数で管理する ことで、この処理をプログラムに実装することができそうです。

$(x_1,y_1)$と$(x_k,y_k)$の関係式は、文字を使って$(x_1,y_1)=(c^\prime x_k+d^\prime y_k,e^\prime x_k+f^\prime y_k)$と表せます。
同様に、$(x_1,y_1)$と$(x_{k+1},y_{k+1})$の関係式も$(x_1,y_1)=(cx_{k+1}+dy_{k+1},ex_{k+1}+fy_{k+1})$と表せます。

すると、前者に$(x_k,y_k)$と$(x_{k+1},y_{k+1})$の関係式を代入することで、係数$c,d,e,f$をそれぞれ$c^\prime,d^\prime,e^\prime,f^\prime$を使った式で表すことができます。

  • $(x_1,y_1)=(c^\prime x_k+d^\prime y_k,e^\prime x_k+f^\prime y_k)$に$(x_k,y_k)=(y_{k+1},x_{k+1}-q_k y_{k+1})$を代入すると、$(x_1,y_1)=(c^\prime y_{k+1}+d^\prime(x_{k+1}-q_k y_{k+1}),e^\prime y_{k+1}+f^\prime(x_{k+1}-q_k y_{k+1}))$
  • 式を整理すると、$(x_1,y_1)=(d^\prime x_{k+1}+(c^\prime-q_kd^\prime)y_{k+1},f^\prime x_{k+1}+(e^\prime-q_kf^\prime)y_{k+1})$
    ($q_k$は$k$番目の方程式における$a$を$b$で割った商を表します)

したがって、各係数の関係式は次のようになります。

  • $c=d^\prime$
  • $d=c^\prime-q_kd^\prime$
  • $e=f^\prime$
  • $f=e^\prime-q_kf^\prime$

初期値と計算終了時の特殊解の求め方を考える

続いて、互除法の計算を始めるときの係数$c,d,e,f$の初期値と、計算が終わったときの特殊解の求め方も一般化してみましょう。

まずは、各係数の初期値について考えます。
上記の計算では$k=2$から始めましたが、キリが悪いので$k=1$から始めることにします。
このとき、$(x_1,y_1)$と$(x_k,y_k)$の関係式は$(x_1,y_1)$そのものですね。
これを係数に注目して書き直すと$(1\times x_1+0\times y_1,0\times x_1+1\times y_1)$ですから、各係数の初期値は$(c,d,e,f)=(1,0,0,1)$となります。

次に、計算が終わったときの特殊解の求め方について考えます。
前述の$90x+37y=1$の特殊解を求める例では、$n$番目の方程式で$b=0$となったら、$(x_n,y_n)=(1,0)$を代入することで特殊解を求めました。
これを一般化すると、$(x_1,y_1)=(cx_n+dy_n,ex_n+fy_n)$に$(x_n,y_n)=(1,0)$を代入するので、$(x_1,y_1)=(c,e)$が求める特殊解となります。

実装

以上から、拡張ユークリッドの互除法を再帰関数を使わずに実装する方法は次のようになります。

extended_euclid(a, b) ($a,b$は非負整数) は、
手順1: 変数$c,d,e,f$をそれぞれ$1,0,0,1$で初期化する。
手順2: $b$の値を調べる。
手順3: $b=0$ならば、$(c,e)$を返す。
手順4: $b\neq 0$ならば、変数$c,d,e,f$にそれぞれ$d,c-qd,f,e-qf$を代入する。その後、変数$a,b$にそれぞれ$b,r$を代入して、手順2に戻る。

コード例

C++

C++では、計算した値を一時的に格納しておくための変数$g$も用意します。
例えば、変数$c,d$にそれぞれ$d,c-qd$を代入する処理は、まず変数$g$に$c-qd$を代入しておき、それから変数$c$に$d$を、変数$d$に$g$を代入します。

void extended_euclid(long long a, long long b, long long& x, long long& y) {
    long long c = 1, d = 0, e = 0, f = 1, g;
    while (b != 0) {
        g = c - a / b * d, c = d, d = g;
        g = e - a / b * f, e = f, f = g;
        g = a % b, a = b, b = g;
    }
    x = c, y = e;
}

Python

def extended_euclid(a, b):
    c, d, e, f = 1, 0, 0, 1
    while b != 0:
        c, d = d, c - a // b * d
        e, f = f, e - a // b * f
        a, b = b, a % b
    return (c, e)

例題3 の$90x+37y=1$をこの関数を使って解くときの関数の動作は、以下の図のようになります。

ExtendedEuclid_10.drawio.png

本題からはそれますが、特殊解が求まる直前($k=5$のとき)の$d,f$の値は、驚いたことに最初の$-b,a$とそれぞれ等しくなります。
また、$(x_5,y_5)=(1,0)$の代わりに$(x_5,y_5)=(1,k)$($k$は整数) を代入すると、一般解$(x_1,y_1)=(7-37k,-17+90k)$が求まります。

3. 拡張ユークリッドの互除法の別解法

2. では、拡張ユークリッドの互除法の原理と実装方法について解説しました。
ですが、計算が複雑で直感的に理解しにくいという人もいるかと思います。

そこで、この章では、合同式 を使った拡張ユークリッドの互除法の別解法について解説します。
これを使うと、2-4. で解説した非再帰的な処理をより直感的に実装できるようになります。

合同式が分からない方は、まずこちらのサイトを読んでみてください。

3-1. 原理

例題3 に再登場してもらいます。

例題3’: $90x+37y=1$を満たす整数$(x,y)$の組を1つ求めよ。

まずは、方程式の両辺を$37$で割ったあまりを考えます。
$37y$は$37$の倍数なので、あまりは$0$です。
すると、$90x+37y=1$は合同式を使って次のように表せます。

  • $90x\equiv 1\pmod{37}\ \cdots$①

次に、$37x$を$37$で割ったあまりを考えます。
もちろんあまりは$0$なので、これは合同式を使って次のように表せます。

  • $37x\equiv 0\pmod{37}\ \cdots$②

すると、①の両辺から②の両辺を2回引くことで、$x$の係数がより小さい式を作ることができます。

  • $(90-37\times 2)x\equiv 1-0\times 2\ \pmod{37}$
    $\Leftrightarrow 16x\equiv 1\pmod{37}\ \cdots$③

$x$の係数が$16$になりました。
同様にして、②,③を使えば$x$の係数をさらに小さくすることができ、これを繰り返せば最終的には$x$の係数が$1$になって、解を求めることができそうです。

さて、ここまでくればお分かりかと思いますが、①,②,③の$x$の係数は順に$90,37,16$となっており、これは ユークリッドの互除法の計算そのもの ですね。
つまり、左辺が互除法の計算になるように式を足し引きすればよいのです。

始めから通して計算してみると、次のようになります。

ExtendedEuclid_Another_1.drawio.png

したがって、⑤より$x$の特殊解の1つは$7$であると分かりました。
対応する$y$の特殊解は、$90x+37y=1$に$x=7$を代入すると$37y=1-90\times 7=-629\Leftrightarrow y=-17$と求まります。
また、⑤より$x$を$37$で割ったあまりが$7$なので、一般解も$x=37k+7$($k$は整数) と求めることができます。($k$を$-k$に置き換えると 2-1. の公式と一致します)

いかがでしょうか。
2. の解法と比べると、計算を逆にたどる必要がない分、より直感的で分かりやすくなったと思います。

yの特殊解を求める

先程は$y$の特殊解を方程式に$x$を代入して求めました。
普通に求める場合はこれでもよいですが、プログラムでは$a\times x$の計算でオーバーフローする可能性があります。
そこで、例題3’ の$y$の特殊解も拡張ユークリッドの互除法で求めてみましょう。

まずは、$90x+37y=1$の両辺を$90$で割ったあまりを考えます。
$90x$を$90$で割ったあまりは$0$なので、この方程式は合同式を使って次のように表せます。

  • $37y\equiv 1\pmod{90}\ \cdots$②’

次に、$90y$を$90$で割ったあまりは$0$なので、これは合同式を使って次のように表せます。

  • $90y\equiv 0\pmod{90}\ \cdots$①’

なお、式の番号は$x$の係数と合うようにあえて逆につけています。

そして、これを$x$の特殊解と同様に計算すると、次のようになります。

ExtendedEuclid_Another_2.drawio.png

したがって、⑤’より$y$の特殊解の1つは$-17$と求まりました。
また、⑤’より$y$を$90$で割ったあまりが$-17(\equiv 73)$なので、一般解も$y=90k-17$($k$は整数) と求めることができます。

3-2. 非再帰関数による実装

3-1. でおこなった計算を一般化してみましょう。
なお、以降は$\mathrm{mod}$を省略します。

処理を一般化する

  • $ax\equiv s\ \cdots(A)$
  • $bx\equiv t\ \cdots(B)$
  • $rx\equiv u\ \cdots(C)$

まずは、$(A),(B)$の2式から$(C)$を求める処理を考えます。
左辺の関係式は$r=a-bq$ですから、これを式全体に当てはめると$(C)=(A)-(B)\times q$です。
したがって、右辺の関係式は$u=s-qt$となります。

次に、これをユークリッドの互除法の処理に合うように言い換えます。
ユークリッドの互除法では「$a$と$b$の最大公約数」から「$b$と$r$の最大公約数」を求めたので、これに合うように 3-1. の計算を言い換えてみましょう。

  • $ax\equiv c^\prime\ \cdots(A)^\prime,\ bx\equiv d^\prime\ \cdots(B)^\prime$ の2式から、
    $bx\equiv c\ \cdots(C)^\prime,\ rx\equiv d\ \cdots(D)^\prime$ の2式を求める

$(B)^\prime$と$(C)^\prime$は同じ式なので、$c=d^\prime$です。
また、先程求めた$u=s-qt$を$(D)^\prime$に当てはめれば、$d=c^\prime-qd^\prime$となります。
これで右辺の関係式が求まりました。

$y$の特殊解についても考えましょう。

  • $ay\equiv e^\prime,\ by\equiv f^\prime$ の2式から、
    $by\equiv e,\ ry\equiv f$ の2式を求める

$x$の特殊解を求めるときと同じですね。
同様に求めると、$e=f^\prime,f=e^\prime-qf^\prime$となります。

初期値と計算終了時の特殊解の求め方を考える

2-4. と同様に、$c,d,e,f$の初期値と、計算が終わったときの特殊解の求め方を考えます。

$c,d,e,f$の初期値は、3-1. を見ればすぐに分かります。
$x$の特殊解については、$90x\equiv 1\ \cdots$① と$37x\equiv 0\ \cdots$② より$(c,d)=(1,0)$ですね。
$y$の特殊解については、$90y\equiv 0\ \cdots$①’ と$37y\equiv 1\ \cdots$②’ より$(e,f)=(0,1)$です。

計算が終わったときの特殊解の求め方は、$b=0$のとき$a=1$なので、$ax\equiv c$の右辺の$c$が$x$の特殊解、$ay\equiv e$の右辺の$e$が$y$の特殊解となります。

実装

以上から、拡張ユークリッドの互除法の別解法を実装する方法は次のようになります。

extended_euclid(a, b) ($a,b$は非負整数) は、
手順1: 変数$c,d,e,f$をそれぞれ$1,0,0,1$で初期化する。
手順2: $b$の値を調べる。
手順3: $b=0$ならば、$(c,e)$を返す。
手順4: $b\neq 0$ならば、変数$c,d,e,f$にそれぞれ$d,c-qd,f,e-qf$を代入する。その後、変数$a,b$にそれぞれ$b,r$を代入して、手順2に戻る。

これは 2-4. で求めた方法と全く同じですね。
このように、メジャーな解法と別解法のどちらからも、この実装方法を求めることができます。
とはいえ、2-4. と比べると別解法のほうが直感的に実装できるかと思います。

コード例

コードは 2-4. と同じですが、再度載せておきます。

C++

void extended_euclid(long long a, long long b, long long& x, long long& y) {
    long long c = 1, d = 0, e = 0, f = 1, g;
    while (b != 0) {
        g = c - a / b * d, c = d, d = g;
        g = e - a / b * f, e = f, f = g;
        g = a % b, a = b, b = g;
    }
    x = c, y = e;
}

Python

def extended_euclid(a, b):
    c, d, e, f = 1, 0, 0, 1
    while b != 0:
        c, d = d, c - a // b * d
        e, f = f, e - a // b * f
        a, b = b, a % b
    return (c, e)

例題3’ をこの関数を使って解くときの関数の動作は、以下の図のようになります。

ExtendedEuclid_Another_3.drawio.png

4. 拡張ユークリッドの互除法の応用 - mod p における逆元

ここまで、拡張ユークリッドの互除法を実装する方法を解説してきました。
最後に、拡張ユークリッドの互除法を応用する場面を紹介します。

それは、$\mathrm{mod}\ p$における逆元 を求めるときです。
$\mathrm{mod}\ p$における逆元って何?という方は、まずは @drken さん著のこちらの記事を読んでみてください。めっちゃ分かりやすいです

簡単に説明すると、$a$にある数を掛けた値が$1$となるとき、その数を「$a$の逆元」と言います。

例として、普通の実数の計算における$a(\neq 0)$の逆元を考えます。
すると、$\displaystyle a\times\frac{1}{a}=1$なので、$a$の逆元は$\displaystyle \frac{1}{a}$です。
普通の実数の計算では、自然数$a$の逆元は分数ですね。

一方、$\mathrm{mod}\ p$における計算では、自然数$a$の逆元は自然数になります。
例えば、$\mathrm{mod}\ 13$における$5$の逆元を考えてみます。
すると、$5\times 8=40\equiv 1\pmod{13}$なので、$\mathrm{mod}\ 13$における$5$の逆元は$8$です。

では、$\mathrm{mod}\ m$($m$は素数) における自然数$a$の逆元$x$を求める方法を考えます。(便宜上$p$を$m$に変えました)

「$a$に$x$を掛けると$1$になる」ですから、合同式で表すと$ax\equiv 1\pmod{m}$です。
これは 3-1. で出てきた式とほとんど同じですね。
つまり、$ax+my=1$における$x$の特殊解を拡張ユークリッドの互除法で求めればよいです。

逆元を求めるにあたって必要なのは$x$の値だけですので、$y$の値を求める計算は省いてよいです。
2-4. および 3-2. の非再帰関数を使った方法では$x$と$y$の値を別々に求めることができるので、こちらを使いましょう。
また、拡張ユークリッドの互除法では$x$の値が負になることもあり得ますが、今回は正の値が欲しいので、負の場合は$x$に$m$を足すことにします。

以上から、$\mathrm{mod}\ m$における$a$の逆元を求める関数 mod_inv(a, m) は次のように実装できます。

mod_inv(a, m) ($0\lt a\lt m$,$m$は素数) は、
手順1: 変数$b$を$m$で初期化する。
手順2: 変数$c,d$をそれぞれ$1,0$で初期化する。
手順3: $b$の値を調べる。
手順4: $b=0$ならば、$c$を正の値に直して返す。
手順5: $b\neq 0$ならば、変数$c,d$にそれぞれ$d,c-qd$を代入する。その後、変数$a,b$にそれぞれ$b,r$を代入して、手順3に戻る。

コード例

C++

long long mod_inv(long long a, long long m) {
    long long b = m, c = 1, d = 0, g;
    while (b != 0) {
        g = c - a / b * d, c = d, d = g;
        g = a % b, a = b, b = g;
    }
    return (c + m) % m;
}

Python

def mod_inv(a, m):
    b, c, d = m, 1, 0
    while b != 0:
        c, d = d, c - a // b * d
        a, b = b, a % b
    return (c + m) % m

おわりに

ここまで、拡張ユークリッドの互除法の実装方法とその応用について解説しました。
拡張ユークリッドの互除法の実装は少し複雑なので、この記事で紹介した方法を実際に紙に書いて実験してみると、さらに理解が深まると思います。

この記事で誤りや表現を改善したほうがよい箇所などがありましたら、コメント欄で教えていただけると嬉しいです。
最後まで記事をご覧いただきありがとうございました。

参考

この記事を書くにあたって参考にしたサイトなどを載せました。
興味のある方はこちらも読んでみてください。

1. ユークリッドの互除法

2. 拡張ユークリッドの互除法

3. 拡張ユークリッドの互除法の別解法

  • 合同式(mod)の意味とよく使う６つの性質 | 高校数学の美しい物語
    https://manabitimes.jp/math/683
  • (書籍) 増補改訂版 チャート式基礎からの数学I+A | チャート研究所 | p.509

4. 拡張ユークリッドの互除法の応用 - mod p における逆元

  1. GCD は最大公約数を表す英語 "Greatest Common Divisor" の略称です。 ↩

  2. ユークリッドの互除法を実装する方法を紹介しているサイトを調べたところ、その多くがどういうわけか$b=0$のほうを採用しています。
    理由は分かりません。 ↩

  3. $x,y$の範囲を実数にしてしまうと、$x$にどんな値を代入してもそれに対応する$y$の解が存在してしまうので、方程式を解く意味がなくなってしまいます。
    そのため、$x,y$の範囲を整数に制限しています。 ↩

  4. $a$と$b$の最大公約数が$1$のとき、「$a$と$b$は互いに素である」といいます。 ↩

  5. 方程式の$y$の係数が$0$なので、$y$がどんな整数でも特殊解は求まりますが、$y=0$とすると最終的に求まる特殊解の$x,y$の絶対値の和が最小になります。 ↩

4
3
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
3

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?