週末、2018年の数学系アドベントカレンダーを読もうと思って日曜数学 Advent Calendar 2018を眺めていたら1日目から早速tsujimotterさんの面白い記事を見つけました。
パスカルの三角形にたくさん出てくる数: 3003 - tsujimotterのノートブック
まずは上の記事をぜひ読んでいただきたいのですが、途中に出てくるSingmaster予想は特に面白い予想だなと思いました。
# Singmaster予想
N(a)をaがパスカルの三角形の中に出現する回数を表すとすると、
aが1より大きい正の整数であるときN(a)には上限値が存在する。
https://en.wikipedia.org/wiki/Singmaster%27s_conjecture
パスカルの三角形は二項展開における係数を三角形状に並べたものです。二項展開は$x+y$のような二つの項からなる式のべき乗を展開したもので、その係数は二項係数と呼ばれます。
\begin{matrix}
(x + y)^0 &=& 1 \\
(x + y)^1 &=& x + y \\
(x + y)^2 &=& x^2 + 2xy + y^2 \\
(x + y)^3 &=& x^3 + 3x^2y + 3xy^2 + y^3 \\
&\cdots&
\end{matrix}
二項係数を順番に並べると
\begin{matrix}
&&&1&&& \\
&&1&&1&& \\
&1&&2&&1& \\
1 & & 3 & & 3 & & 1 \\
&&& \cdots &&&
\end{matrix}
このような三角形を作ることができます。これがパスカルの三角形です。
ある数がパスカルの三角形に出現する回数を数える
Singmaster予想はある数$a$がパスカルの三角形の中に出現する回数$N(a)$に関する予想でした。となると実際に$N(a)$を計算してみたくなるのが人間というものです。tsujimotterさんの記事によれば現在知られている$N(a)$の最大値は8で、$N(a)=8$となる最小の$a$は3003だそうです。なのでここでは$N(3003)$まで計算することを目標にしてみましょう。
まずはパスカルの三角形を用意します。二項展開をいちいち計算するのは手間がかかりますが、パスカルの三角形のn段k番目の値は${}_n{\rm C}_k$で計算できることが知られているのでこれを使いましょう。組み合わせの数は階乗を用いて
{}_n{\rm C}_k = \frac{n!}{(n-k)!k!}
と計算することができます。
以上の概念をプログラムで実装していきましょう。まずは階乗計算です。
fact :: Int -> Integer
fact 0 = 1
fact n = fromIntegral n * fact (n-1)
階乗計算は再帰を使って簡単に書くことができます。引数の型はIntですが階乗の計算結果はとても大きくなる可能性があるため多倍長整数の型であるIntegerを返り値の型に使用しています(fromIntegralを使ってるのはそのためです)。組み合わせの数は
combination :: Int -> Int -> Integer
n `combination` k = fact n `div` (fact (n-k) * fact k)
のように実装できます。最後にパスカルの三角形は
pascal :: [Integer]
pascal = [n `combination` k | n <- [0..], k <- [0..n]]
と実装できます。これはパスカルの三角形の無限リストになっていますが、遅延評価のおかげで必要な分だけ取り出して使うことができます。試しに最初の10個だけ取り出してみましょう。
$ take 10 pascal
[1,1,1,1,2,1,1,3,3,1]
パスカルの三角形は1を除けば下の段に行くほどどんどん大きい数しか出てこなくことがわかります。特に1より大きい正の数$a$は$a$段目までにしか出てきません(1番上を0段目と数えていることに注意)。なのでaの出現回数を数えるためにはpascalの有限個の要素を評価すれば十分です。この評価する要素の数はa+1番目の三角数として計算することができます。
tri :: Int -> Int
tri n = n * (n+1) `div` 2
あとは出現する回数を数えるだけです。
countInPascal :: Int -> Int
countInPascal a = length . filter (== fromIntegral a) $ take (tri (a+1)) pascal
以上をまとめて3003までの数がパスカルの三角形に出現する回数を数えてみましょう。
main :: IO ()
main = for_ [2..3003] $ \a ->
let n = countInPascal a
in putStrLn $ "N(" ++ show a ++ ") = " ++ show n
Repl.itにコードを載せておいたので実際に実行してみてください。
https://repl.it/repls/BlindExtrasmallSpof
$ runhaskell Main.hs
N(2) = 1
N(3) = 2
N(4) = 2
N(5) = 2
N(6) = 3
N(7) = 2
N(8) = 2
N(9) = 2
N(10) = 4
N(11) = 2
N(12) = 2
...
実行すると軽快に計算が開始されると思います。しかしどんどん遅くなってとても待てる時間内に3003まで計算できる気配がありません。試しに簡単なコードを書いて実行時間を測ってみましょう。
-- | 与えられたアクションの実行に掛かった時間を表示する
showElapsedTime :: IO a -> IO a
showElapsedTime action = do
start <- getCurrentTime
a <- action
end <- getCurrentTime
print $ end `diffUTCTime` start
pure a
main :: IO ()
main = showElapsedTime $
for_ [2..500] $ \a ->
let n = countInPascal a
in putStrLn $ "N(" ++ show a ++ ") = " ++ show n
3003まではとても終わらなさそうなのでとりあえず500まで計算してみます。Repl.it上で実行してみると、

なんと8分43秒もかかってしまいました!これでは3003に到達するまで途方もない時間がかかってしまいます…
プロファイリング
なぜこんなに遅くなってしまったのでしょうか。無邪気にコードを書いていたので思い当たる節は色々ありますが、何はともあれまずはプロファイリングをしてみましょう。Repl.itからローカルのstackプロジェクトにコードを持ってきます(ちなみにローカルのMacBookProだとN(500)までの計算は約0.75秒で終わりました)。stackで管理しているコードのプロファイルを行うには
$ stack build --profile
のようにビルド時に--profileオプションを渡してやればOKです1。そして実行時にプロファイルを行いたい項目に対応するオプションを渡します。時間プロファイルを行いたい場合は-pを渡して実行してやればOKです2。
$ stack exec -- pascal-exe +RTS -p
実行すると.profファイルが生成されていてプロファイルの実行結果が出力されています。
Mon Jan 14 00:30 2019 Time and Allocation Profiling Report (Final)
pascal-exe +RTS -N -p -RTS
total time = 0.76 secs (2597 ticks @ 1000 us, 12 processors)
total alloc = 7,225,801,320 bytes (excludes profiling overheads)
COST CENTRE MODULE SRC %time %alloc
fact Main app/Main.hs:(306,1)-(307,23) 84.8 99.0
countInPascal Main app/Main.hs:327:1-81 9.6 0.0
combination Main app/Main.hs:312:1-54 4.7 0.8
...
これを見るとどうやらfactの計算に85%近くの時間を費やしているようです。
fact のメモ化
factは再帰で定義されているのでfact nを計算するにはfact 0に到達するまでn回計算しないといけません。パスカルの三角形の計算が進むにつれ計算する階乗の値も大きくなっていくため、これが負担になっているのでしょう。そこでfactをメモ化して一度計算した値を再計算しないようにしましょう。factは純粋な関数なので気軽に副作用を起こすことができません。なのでまずは遅延評価を利用したメモ化を実装してみましょう3。
-- | 関数をメモ化する関数
memoize :: (Int -> a) -> Int -> a
memoize f = (map f [0..] !!)
fact :: Int -> Integer
fact = memoize fact'
where
fact' 0 = 1
fact' n = fromIntegral n * fact' (n-1)
メモ化を実装してローカルで$N(500)$までの計算を実行してみると約0.4秒で計算が終わりました。最適化が成功しましたね ![]() 今度は$N(3003)$まで計算してみましょう。
今度は$N(3003)$まで計算してみましょう。
...
N(3002) = 2
N(3003) = 8
236.503356s
約3分56秒と時間はかかりましたが確かに3003がパスカルの三角形の中に8回登場することを確認することができました ![]()
Mapを使った数え上げ
当初の目標であった$N(3003)$までの計算は達成しましたが、まだまだ計算時間は縮められそうです。$N(3003)$を計算したプログラムのプロファイルは
COST CENTRE MODULE SRC %time %alloc
countInPascal Main app/Main.hs:334:1-81 55.8 0.0
memoize Main app/Main.hs:307:1-28 25.1 0.0
combination Main app/Main.hs:319:1-54 18.3 63.0
fact.fact' Main app/Main.hs:(313,5)-(314,42) 0.6 33.8
pascal Main app/Main.hs:324:1-54 0.1 3.2
となっていて、次はcountInPascalに手を加えるのが良さそうです。countInPascalでは与えられた数が出現する回数をpascalを線形に走査することで計算していますが、3003までのすべての数でこれを繰り返すのは無駄が多いです。なので1回の走査である数以下の数の出現回数をすべて計算するような関数を実装してみます。
-- | パスカルの三角形の中に与えられた数以下の数が出現する回数の辞書を計算する
occurrence :: Int -> Map Integer Int
occurrence 1 = error "occurrence can't take 1"
occurrence a = foldr go Map.empty (take (tri (a + 1)) pascal)
where
a' = fromIntegral a
go x = if x <= a' then Map.insertWith (+) x 1 else id
main :: IO ()
main = showElapsedTime $ do
let result = occurrence 3003
for_ [2..3003] $ \a ->
let n = result Map.! a
in putStrLn $ "N(" ++ show a ++ ") = " ++ show n
実行してみると約1分43秒で$N(3003)$まで計算することができました ![]()
木を使ったメモ化
再びプロファイルを見てみると
COST CENTRE MODULE SRC %time %alloc
memoize Main app/Main.hs:310:1-28 55.7 0.0
combination Main app/Main.hs:323:1-54 42.4 62.3
fact.fact' Main app/Main.hs:(317,5)-(318,42) 1.4 33.3
occurrence Main app/Main.hs:(342,1)-(346,57) 0.2 1.2
pascal Main app/Main.hs:328:1-54 0.2 3.1
メモ化の実装であるmemoizeが律速になっているようです。memoizeはリストの遅延評価を利用してメモ化を行う関数でしたがメモ化した値を参照するために(!!)を使っていました。リストの要素に対するアクセスはO(n)の時間がかかってしまうため時間的には不利です。なので今回はメモ化のためにO(log n)で要素にアクセスできる木を自分で作ってメモ化を改良してみることにします。実装はtanakhさんの
Haskellでメモ化を行うもう一つの方法 - 純粋関数型雑記帳
という記事を参考に行いました。
-- | メモ化する関数の引数となれる型
-- インスタンスとなる型は非負のIntegerと同型になる必要がある
class MemoIx a where
index :: a -> Integer
unindex :: Integer -> a
-- | 整数を非負整数に埋め込む
instance MemoIx Integer where
index n | n >= 0 = n * 2
| otherwise = -n * 2 - 1
unindex n | n `mod` 2 == 0 = n `div` 2
| otherwise = -((n+1) `div` 2)
-- | 木
data Tree a = Tree (Tree a) a (Tree a)
-- | メモ化する関数の返り値を保持する木を生成する
genTree :: MemoIx a => (a -> b) -> Tree b
genTree f = gen 0
where
gen i = Tree (gen $ i * 2 + 1) (f $ unindex i) (gen $ i * 2 + 2)
-- | メモ化した木が保持する情報を検索する
findTree :: MemoIx a => Tree b -> a -> b
findTree tree i = go (bits $ index i + 1) tree
where
go [] (Tree _ v _) = v
go (0:bs) (Tree l _ _) = go bs l
go (_:bs) (Tree _ _ r) = go bs r
bits = tail . reverse . map (`mod` 2) . takeWhile (>0) . iterate (`div` 2)
-- | 関数をメモ化する関数
memoize :: MemoIx a => (a -> b) -> a -> b
memoize f = findTree (genTree f)
実行してみると約1分22秒で$N(3003)$まで計算することができました。少しずつ早くなってきています。
数学的な性質を利用する
再びプロファイルを見てみると
COST CENTRE MODULE SRC %time %alloc
combination Main app/Main.hs:356:1-54 77.5 36.5
findTree.bits Main app/Main.hs:339:5-78 12.2 39.4
findTree.go Main app/Main.hs:(335,5)-(337,36) 4.9 0.0
fact.fact' Main app/Main.hs:(350,5)-(351,42) 2.2 19.5
findTree Main app/Main.hs:(333,1)-(339,78) 0.7 1.1
pascal Main app/Main.hs:361:1-54 0.4 1.8
どうやら今度はcombinationの計算がボトルネックになっているようです。combinationの計算を早くするために組み合わせの数の数学的な性質を利用してみましょう。
{}_n{\rm C}_k = {}_{n-1}{\rm C}_{k-1} + {}_{n-1}{\rm C}_k
この性質はパスカルの三角形の要素の値が左上の値と右上の値を足し合わせることで計算できることを示しています。これを見るとcombinationは階乗を直接計算しなくても再帰的なアルゴリズムで計算できることがわかります。
combination :: Int -> Int -> Integer
n `combination` 0 = 1
n `combination` k =
| n == k = 1
| otherwise = (n-1) `combination` (k-1) + (n-1) `combination` k
しかしこのままではまた再帰計算がボトルネックになってしまうことは目に見えてるので、メモ化も行いましょう。
instance (MemoIx a, MemoIx b) => MemoIx (a, b) where
index (a, b) =
let ia = index a
ib = index b
in (ia + ib) * (ia + ib + 1) `div` 2 + ib
unindex i =
let w = floor $ (sqrt (8 * fromIntegral i + 1) - 1) / 2
t = w * (w + 1) `div` 2
ib = i - t
ia = w - ib
in (unindex ia, unindex ib)
-- | 組み合わせの数
combination :: Int -> Int -> Integer
n `combination` k = memoize c (n, k)
where
c (_, 0) = 1
c (n, k)
| n == k = 1
| otherwise = (n-1) `combination` (k-1) + (n-1) `combination` k
タプルの引数の関数をメモ化するために自然数のペアと自然数の間の全単射写像 ${\mathbb N}\times{\mathbb N}\rightarrow{\mathbb N}$である対関数と呼ばれるものを使用しています。実行してみると約49秒で$N(3003)$まで計算することができました。ついに1分を切りました ![]()
メモ化、そしてState
再びプロファイルを見てみると
COST CENTRE MODULE SRC %time %alloc
findTree.bits Main app/Main.hs:339:5-78 49.7 83.8
findTree.go Main app/Main.hs:(335,5)-(337,36) 24.1 0.0
genTree.gen Main app/Main.hs:329:5-68 4.1 3.6
index Main app/Main.hs:(355,3)-(358,46) 3.6 2.6
combination.c Main app/Main.hs:(372,5)-(375,69) 2.6 2.5
...
findTreeが約74%の計算時間を占めていることがわかります。やはり自作ではなく枯れているライブラリのデータ構造を使うのが良さそうなので、既に出現回数のカウントに使用しているMapを使ってメモ化を行いたいと思います。しかしMapは遅延評価の仕組みを使って要素を後から組み立てることができません。そこでStateモナドを使ってcombinationの入出力を保持するMapを管理しようと思います。それに伴って関連するすべての関数をStateに対応させていきます。
type Memo = Map (Int, Int) Integer
combination :: Int -> Int -> State Memo Integer
_ `combination` 0 = pure 1
n `combination` k
| n == k = pure 1
| otherwise = do
m <- get
case Map.lookup (n, k) m of
Just a -> pure a
Nothing -> do
a1 <- combination (n-1) (k-1)
a2 <- combination (n-1) k
let a = a1 + a2
modify $ Map.insert (n, k) a
pure a
-- | パスカルの三角形
pascal :: Int -> State Memo [Integer]
pascal upper = sequence [combination n k | n <- [0..upper], k <- [0..n]]
-- | パスカルの三角形の中に与えられた数以下の数が出現する回数の辞書を計算する
occurrence :: Int -> Map Integer Int
occurrence 1 = error "occurrence can't take 1"
occurrence a = foldr go Map.empty $ evalState (pascal a) Map.empty
where
a' = fromIntegral a
go x = if x <= a' then Map.insertWith (+) x 1 else id
実行してみると約11秒で$N(3003)$まで計算することができました。だいぶ速くなりましたね!
SCC
さてプロファイルを見てみると
COST CENTRE MODULE SRC %time %alloc
combination Main app/Main.hs:(312,1)-(324,16) 85.4 78.0
pascal Main app/Main.hs:328:1-74 5.9 11.2
combination.a Main app/Main.hs:322:15-25 5.1 9.6
occurrence.go Main app/Main.hs:337:5-57 2.3 0.1
このようにcombinationが約85%の計算時間を占めていることがわかります。しかしcombinationはコード量が多く、どこが本当のボトルネックになっているのかがわかりません。そんなときはSCC(Set Cost Centre)と呼ばれるものを使ってより詳細なプロファイルを取ることができます4。SCCを挿入したcombinationは以下のようになります。
combination :: Int -> Int -> State CombinationMemo Integer
_ `combination` 0 = pure 1
n `combination` k
| n == k = pure 1
| otherwise = do
m <- get
case {-# SCC "combination:Map.lookup" #-} Map.lookup (n, k) m of
Just a -> pure a
Nothing -> do
a1 <- combination (n-1) (k-1)
a2 <- combination (n-1) k
let a = a1 + a2
modify $ {-# SCC "combination:Map.insert" #-} Map.insert (n, k) a
pure a
Mapの探索と挿入の処理がボトルネックになっているとあたりをつけに行っています。この状態でプロファイルを取ってみると
COST CENTRE MODULE SRC %time %alloc
combination:Map.lookup Main app/Main.hs:317:49-67 41.3 1.3
combination:Map.insert Main app/Main.hs:323:57-75 36.8 63.5
combination Main app/Main.hs:(312,1)-(324,16) 7.8 13.2
pascal Main app/Main.hs:328:1-74 5.5 11.2
combination.a Main app/Main.hs:322:15-25 4.8 9.6
occurrence.go Main app/Main.hs:337:5-57 2.5 0.1
となり、やはりMapの処理に時間がかかっていることがわかりました。
探索空間を減らす
プロファイルを見るとMap.lookupが律速になっているようです。とはいえこれはライブラリの関数なので手を加えることができません。そこでMap.lookupが必要になる探索空間を減らすというアプローチで攻めて見ることにしましょう。実際パスカルの三角形に無数に現れる1は考える必要がありませんし、パスカルの三角形は左右対称な形をしているので探索空間も半分に減らせるはずです。
-- | パスカルの三角形の半分
pascalHalf :: Int -> State Memo [Integer]
pascalHalf upper = sequence [combination n k | n <- [1..upper], k <- [1..n `div` 2]]
-- | パスカルの三角形の真ん中
pascalCenter :: Int -> State Memo [Integer]
pascalCenter upper = sequence [combination n (n `div` 2 + 1) | n <- [1..upper], n `mod` 2 == 1]
-- | パスカルの三角形の中に与えられた数以下の数が出現する回数の辞書を計算する
occurrence :: Int -> Map Integer Int
occurrence 1 = error "occurrence can't take 1"
occurrence a = flip evalState Map.empty $ do
half <- pascalHalf a
center <- pascalCenter a
let halfMap = foldr go Map.empty half
centerMap = foldr go Map.empty center
result = Map.unionWith (+) centerMap $ Map.map (*2) halfMap
pure result
where
a' = fromIntegral a
go x = if x <= a' then Map.insertWith (+) x 1 else id
実行してみると約10秒とそこまで大きな改善にはなりませんでした。プロファイルは
COST CENTRE MODULE SRC %time %alloc
combination:Map.insert Main app/Main.hs:325:57-75 42.3 65.0
combination:Map.lookup Main app/Main.hs:319:49-67 42.2 1.2
combination Main app/Main.hs:(314,1)-(326,16) 6.4 14.4
combination.a Main app/Main.hs:324:15-25 3.7 10.2
pascalHalf Main app/Main.hs:331:1-84 3.1 8.4
occurrence.go Main app/Main.hs:350:5-57 1.4 0.0
のようになっており、わずかにMap.insertのほうが律速となったようです。だったら次にMap.insertを減らせないかと考えるわけですが、組み合わせの数には
{}_n{\rm C}_k = {}_n{\rm C}_{n-k}
という性質があるので、これを使えばMapに挿入する数もだいたい半分に減らせそうです。
combination :: Int -> Int -> State Memo Integer
_ `combination` 0 = pure 1
n `combination` k
| n == k = pure 1
| n `div` 2 < k = combination n (n - k) -- ここを新たに実装!
| otherwise = ...
これを実行すると約4.8秒となりました。実行時間が半分になり大きな進歩です!プロファイルは
COST CENTRE MODULE SRC %time %alloc
combination:Map.lookup Main app/Main.hs:320:49-67 38.7 1.4
combination:Map.insert Main app/Main.hs:326:57-75 36.8 62.1
combination Main app/Main.hs:(314,1)-(327,16) 8.3 13.5
pascalHalf Main app/Main.hs:332:1-84 6.6 11.9
combination.a Main app/Main.hs:325:15-25 5.3 9.9
...
のようになり依然とMapの処理がボトルネックとなってしまっていますが、もはや為す術はなさそうです。
最終的に出来上がったコードをRepl.itに置いておきます。
https://repl.it/repls/UnwelcomeLightblueUnix
Repl.it上で $N(500)$ まで計算すると、
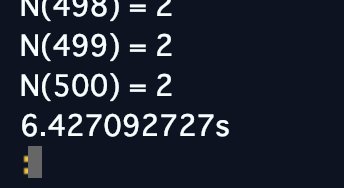
約6.4秒にまで縮めることができていました!最初の8分43秒に比べると約80倍の高速化ができたことになります ![]()
まとめ
最後のボトルネックはMapということになってしまいましたが、これ以上の改善案を思いつかないので今回はこれまでとしましょう。最終的には途方もなく時間がかかりそうだった$N(3003)$までの計算を5秒以内で終わるようにまで改善することができました![]() 。また何か思いついて改善できたらアウトプットしたいと思いますし、最終的にはRepl.it上で動作させるぐらい軽いものにしたいと思っています。もし何か改善のアイデアを思いつく人がいて教えていただけたりするととても嬉しいです。
。また何か思いついて改善できたらアウトプットしたいと思いますし、最終的にはRepl.it上で動作させるぐらい軽いものにしたいと思っています。もし何か改善のアイデアを思いつく人がいて教えていただけたりするととても嬉しいです。
追記: 2019/1/15
@mod_poppo さんからコメント頂き、$N(3003)$の計算が1秒未満にまで短くなりました ![]()
パスカルの三角形自体の計算を再帰的に行うことで組み合わせの数を直接計算することを避けるのがポイントのようです。
追記: 2019/1/16
@kan0u @youmil_rain さんからコメントいただき、パスカルの三角形を斜めに探索することで、Repl.it上でも1秒程度で $N(3003)$ まで計算できるようになりました ![]()
これなら次の $N(a) = 8$ となる数である61218182743304701891431482520まで計算するのも夢ではないかもしれません!
https://qiita.com/lotz/items/b9ca3dfdbe97ad42bd12#comment-c0d9a3134d35a8b7bd6b
https://qiita.com/lotz/items/b9ca3dfdbe97ad42bd12#comment-ed8c6cbcd6f4aa14f2e6
追記: 2019/1/17
上記プログラムを使ってローカルで$a = 200000000$(=2億)まで調べたところ、 $N(a) \geq 5$を満たすものは
N(120) = 6
N(210) = 6
N(1540) = 6
N(3003) = 8
N(7140) = 6
N(11628) = 6
N(24310) = 6
3155.443005s
となりました。24310以降全く現れないのは不思議ですね。
ただこれ以上の数まで計算しようとするとプログラムがkillされてしまったので、次に進むには新たな工夫が必要かもしれません。