Lorenz96モデルのデータ同化:準備編

はじめに

データ同化(Data Assimilation)をJulia言語を用いて行ってみよう、
というのが趣旨です。

一口にデータ同化と言ってもたくさんの手法があるので、
それらのなかで主要なものを紹介していきたいと思います。

この記事では、データ同化の概念を紹介したのち、
扱うモデル(40変数Lorenz96モデル)の性質をJuliaで計算して描画します。

実際にデータ同化をするのは次回以降の記事になります。

これ以降の数値計算はJupyter NotebookにJulia1.1を導入して行っています。¹
Juliaを使う部分だけ興味がある人は、
Lorenz96モデルの計算のところから読んでもらって大丈夫です。

データ同化の考え方

データ同化の概念を簡単に説明します。

まず、時刻$i=1,2,\ldots,N$において、知りたい真のデータ$x_i^t$があったとします。²
真のデータの並び方について、ある程度の規則性が分かっていて、
時間発展させるモデル$M$によって$x_i^t=M(x_{i-1}^t)$と表されているとしましょう。

真のデータは基本的にどこにあるのか分からないので、
代わりに観測データ$y_i$があったとします。
観測データとは知りたい真のデータ$x_i^t$に何らかの確率的な誤差が加わったものです。

$M$と$y_i$を組み合わせて真値$x_i^t$の良い推定をするのがデータ同化です。
図で説明します。

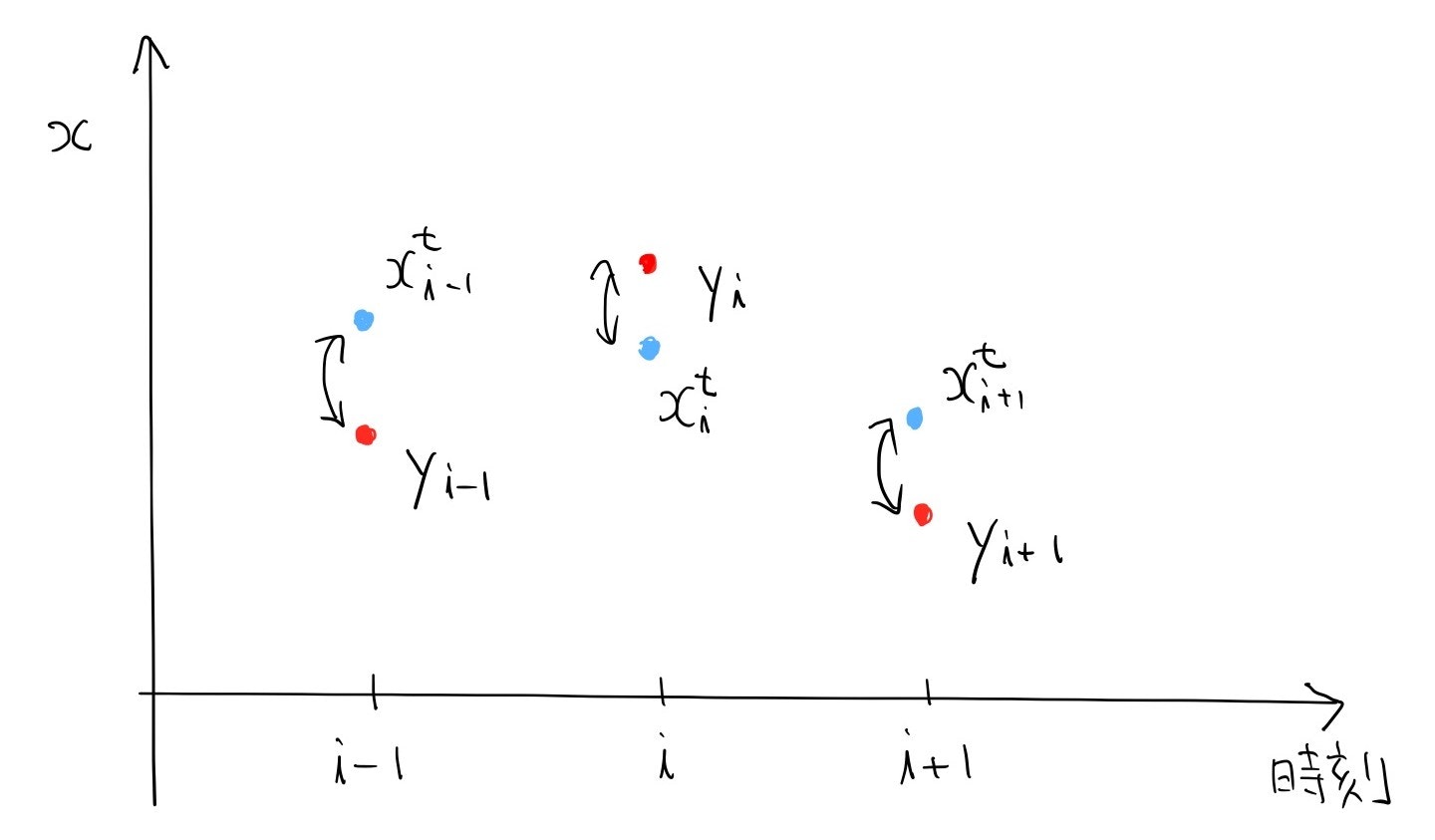
こんな感じに、青い真のデータに誤差が加わった赤い観測データがあります。
真のデータは便宜上描いただけで、本当はどこにあるのかはわかりません。
このままでは各時刻にデータが一つしかないので、推定しようがないです。
そこでモデル$M$の出番です。

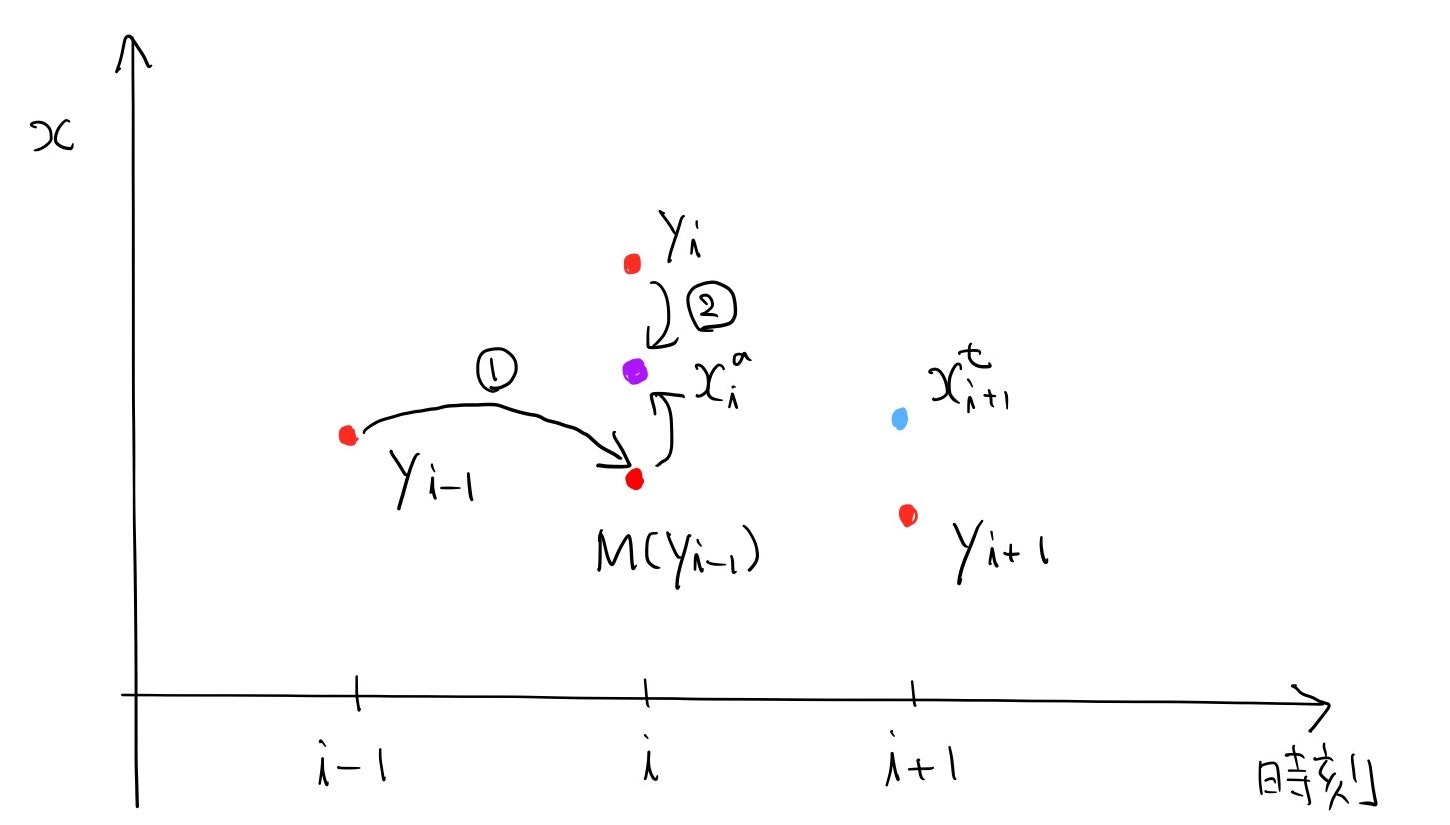
時刻$i-1$の観測データをモデルで時間発展させると、時刻$i$にデータが二つできます。
$M$は短期間ならそれほど誤差を発達させないので、
$M(y_{i-1})$の誤差の大きさは$y_{i-1}$より少し大きい程度です。
すると、観測をそのまま使うよりは良い推定値$x_i^a$を、尤度推定なり最小分散推定なりで
求めることができます。もう一つ分時刻を進めます。

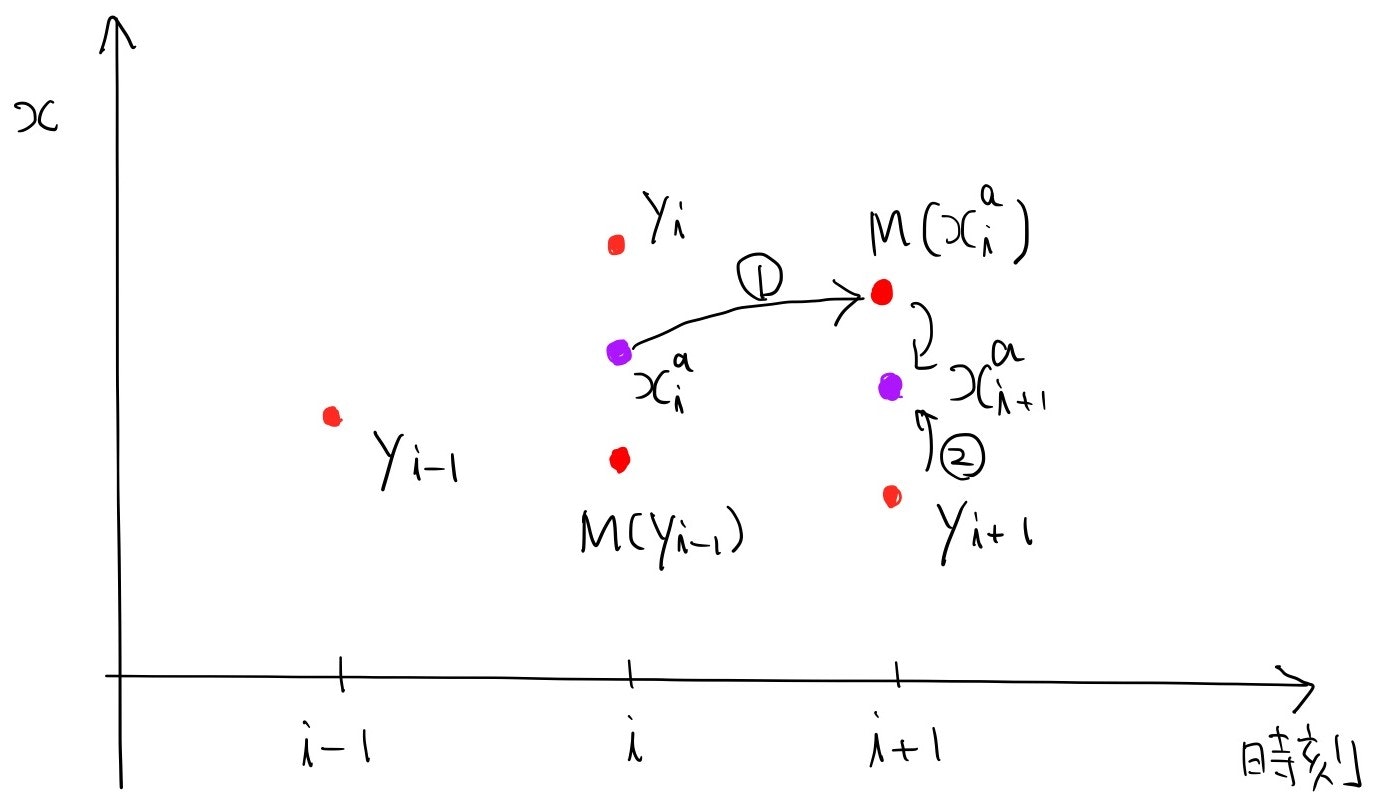
$y_i$ではなく先ほど得られた推定値$x_i^a$をモデルで時間発展させます。
$M(x_i^a)$の誤差の大きさは$x_i^a$より少し大きい程度です。
すると、推定値$x_{i+1}^a$の誤差は、$x_i^a$よりも小さくなるはずです。
これを繰り返していくと、誤差がどんどん小さくなって、ある値付近で飽和することが期待されます(片方のデータは誤差の大きさが決まった観測データなので、0に収束する事はありません)。

飽和した状態になれば、モデルによって時間発展させることで、
観測データを使うよりも良い少し未来の予報が得られます。
これがデータ同化の基本的な考え方です。

実際にデータ同化をする上でまず必要で重要なのは、
モデル$M$が誤差を発達させないような時間の幅を求める(スケーリングをする)ことです。
Lorenz96モデルでそれをするのが、この記事の目標です。

スケーリングの大切さ

スケーリングの重要さを見るために、前節のお気持ちを数式にしてみます。

y_i = x_i^t + \varepsilon_i^o ,\quad \varepsilon_i^o \sim N(0,r) \\
x_i^a = x_i^t + \varepsilon_i^a,\quad \varepsilon_i^a \sim N(0,r_i^a) \\
M(x_{i-1}^a) = x_i^t + \varepsilon_i^f, \quad \varepsilon_i^f \sim N(0,p\times r_{i-1}^a)

という形を仮定します。³

ここで$r>0$は観測データの分散で時間によらず一定、$r_i^a$は推定値の分散、
$\varepsilon_i^o,\varepsilon_i^f$は互いに相関がない確率変数とし、
$p>1$はモデルによる一ステップ当たりの誤差の拡大率としました。

$r_i^a$の漸化式を導出し、極限が$p$にどう依存するかを見ます。

x_i^a = t y_i + (1-t) M(x_{i-1}^a), \quad t \in (0,1)

という形を仮定し、最初の式を代入して分散を計算すると

r_i^a = t^2 r + (1-t)^2 pr_{i-1}^a

となります。これを$t$の関数とみて最小化する(最小分散推定)と、

r_i^a = \frac{rpr_{i-1}^a}{r+pr_{i-1}^a}

という漸化式を得ます。分散を重みとする重み付き平均ですね。
非負単調減少であることはすぐに分かるので、極限は存在し、
上の式で$r^a=r_i^a=r_{i-1}^a$として解くと、極限値$r^a=\lim_{i\to\infty}r_i^a$が

r^a = r \times \frac{p-1}{p}

として求まります。$p=1.2$なら観測誤差の$1/6$倍、$p=2$なら$1/2$倍、
$p=4$なら$3/4$倍です。

データ同化の手法を工夫しても$p=1.2$と$p=2$の差を埋めるのは難しく、
いかに観測誤差の増大率$p$に結果が依存するのかが分かると思います。
$p$は時間間隔に対して指数的に増大するので、スケーリングは重要です。

L96モデル

L96モデルは1996年にLorenzが提唱した気象のモデルで、⁴

\frac{\mathrm{d}u_i}{\mathrm{d}t} = (u_{i+1} - u_{i-2})u_{i-1} - u_{i} + F,\quad i=1,\ldots,N

で与えられます。ただし、
$u_i = u_{N+i}(i\leq 0),u_j=u_{j-N}(j>N)$として周期的にしています。

方程式右辺第1項は移流項、第2項は減衰項、第3項$F$は外力項です。
$u_i = F,i=1,\ldots,N$は右辺の関数の零点すなわち平衡点で、$F$の値によって
安定か不安定かが変わります。早速計算してみましょう。

解の様子

4段4次Runge-Kutta法で数値的に解きます。

using DifferentialEquations
using Plots;gr()

##パラメータ
##Fの大きさで挙動が変わる
F=8.0
N=40

##右辺の関数
function L96!(du,u,p,t)
    for i=3:N-1
        du[i] = (u[i+1]-u[i-2])u[i-1] - u[i] + p
    end
    du[1] = (u[2]-u[N-1])u[N] - u[1] + p
    du[2] = (u[3]-u[N])u[1] - u[2] + p
    du[N] = (u[1]-u[N-2])u[N-1] - u[N] + p
end

##初期条件は全要素がFのベクトルに標準正規分布に従う乱数を載せたもの
u0 = fill(F,N)+randn(N)
##時間積分の区間
tspan = (0.0,20.0)
##方程式の定義
prob = ODEProblem(L96!,u0,tspan,F)

##4段4次Runge-Kuttaで解く
##adaptive=false,dt=0.01で刻み幅を固定
##adaptive=false無しだと動的に刻み幅を変える
##dense=falseで0.01毎の値のみ保存
sol = solve(prob,RK4(),dense=false,adaptive=false,dt=0.01)

##結果をプロット
##1，2，3成分だけ見る
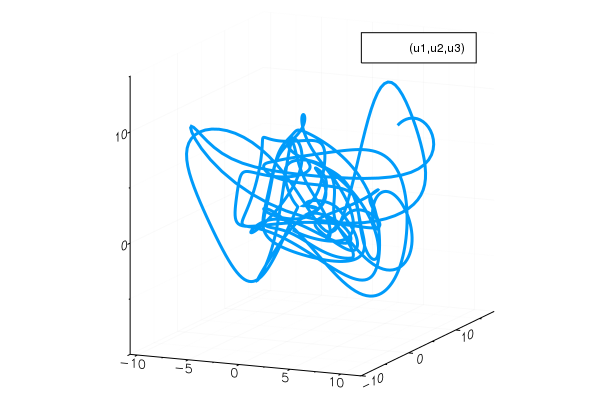
plot(sol,vars=(1,2,3), fmt =:png)

なんとなく3変数のローレンツ方程式と似た雰囲気を感じます。
ある程度の時間発展の後に、
解は崩れた周期軌道(アトラクター)に載ることが分かります。

解くだけなら簡単にできました。
本当は横軸に各成分、縦軸に時刻を取ってheatmapを描きたかったのですが、
調べても良くわからず。
外部ファイルへの出力を経由せず、直接solから描きたいのですが、
方法が分かったら追記します。

スケーリング

誤差の発達率を調べます。
ここではリアプノフ指数を数値的に計算するようにします。

アトラクター上の点を取り、少しだけずらします。⁵
それぞれを時間発展させ、ずらした誤差の成長を記録します。
この操作を何回か繰り返し、平均を取って、誤差の発達率をグラフにします。

using DifferentialEquations
using Plots;gr()
using Statistics

## Fは外力項、Nは成分の数
F=8.0
N=40
##epsilonは摂動の大きさ
epsilon=1e-3
##サンプルの数
sample=40

function L96!(du,u,p,t)
    for i=3:N-1
        du[i] = (u[i+1]-u[i-2])u[i-1] - u[i] + p
    end
    du[1] = (u[2]-u[N-1])u[N] - u[1] + p
    du[2] = (u[3]-u[N])u[1] - u[2] + p
    du[N] = (u[1]-u[N-2])u[N-1] - u[N] + p
end

###まずアトラクターにのるまで時間発展

##全要素がFのベクトルに標準正規分布に従う乱数を載せる
u0 = fill(F,N)+randn(N)
##十分長い時間積分して保存する
tspan = (0.0,100)
prob = ODEProblem(L96!,u0,tspan,F)
sol = solve(prob,RK4(),dense=false,adaptive=false,dt=0.01)

##各サンプルごとに100時間ステップ分の発展を保存
error = Array{Float64}(undef,sample,100)

for i=1:sample

##アトラクター上の点を取る。3000よりは大きくないとアトラクターまで行かない。
##sampleが大きすぎるとここが破綻するので調整
u_attract = copy(sol[:,3000+100i])
##少しだけずらす
u_attract_perturb = u_attract + epsilon * randn(N)

##誤差の時間発展間隔
tspan_attract = (0.0,10.0)

##それぞれ時間積分
prob_attract = ODEProblem(L96!,u_attract,tspan_attract,F)
prob_attract_perturb = ODEProblem(L96!,u_attract_perturb,tspan_attract,F)
    
sol_attract = solve(prob_attract,RK4(),dense=false,adaptive=false,dt=0.01)
sol_attract_perturb = solve(prob_attract_perturb,RK4(),dense=false,adaptive=false,dt=0.01)
　##時間発展を保存
　for j=1:100
　　error[i,j] = norm(sol_attract[j]-sol_attract_perturb[j])
　end
end

##平均を取ってグラフにする
error_mean = mean(error, dims=1)
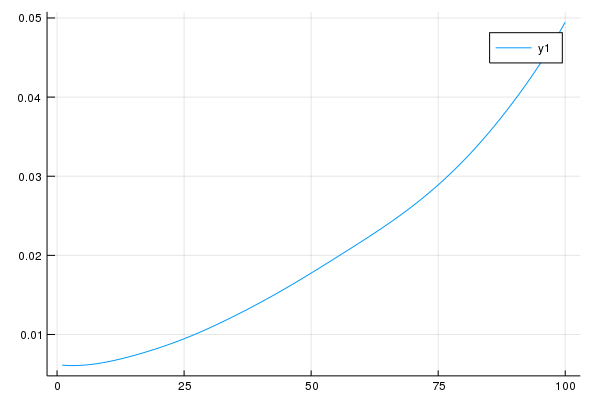
plot(1:100,error_mean[:],fmt=:png)

これを見るとおおよそ40回の反復で誤差が2倍になる事が分かります。
Lorenz96の元論文では、気象データでは2日で誤差が2倍になる事から、
5回の反復すなわち0.05時間ステップを6時間として観測のスケーリングをしています。⁶
これに倣って、今後のデータ同化における観測の間隔は、0.05時間ステップとすることにします。

まとめ

今回の記事ではLorenz96モデルのスケーリングをし、
観測の間隔を0.05時間ステップとすることに決めました。
次回からは実際にデータ同化を実装します。

参考文献

特定の文献を参考にしたわけではないですが、内容の多くは
京都大学理学部で開講しているデータ同化A,Bの講義内容に基づきます。

1. Julia1.2でも動作することを確認しました(12/3)
   私はJulia言語の素人なので至らないところもあるかと思います。
   こう書いた方がいい、などありましたらご指摘いただけると助かります。 ↩

2. 以降現れる$x$の上添え字はobservation、analysis、trueの頭文字です。
   $M$は短期間(添え字一つ分)ならそれほど誤差が増加しないものの、
   長期間だと誤差が指数的に増加して使い物にならなくなるような写像です。
   ローレンツ方程式みたいなカオス性を示す微分方程式を、
   短時間数値計算で時間発展させたものだと思ってください。 ↩

3. $M$は通常非線形なので、正規分布で近似していると思ってください。 ↩

4. Edward Norton Lorenz,1963年に"Determinisitic Nonperiodic Flow"でLorenz方程式を見つけ出した人です。 ↩

5. アトラクター上にいない場合、アトラクターに漸近しようとして誤差が減少することがあります。それを避けるためです。 ↩

6. "Predictability – A problem partly solved". Seminar on Predictability, Vol. I, ECMWF. ↩