CartPoleゲームでDenseとLSTMを比較

はじめに

OpenAI GymのCartPoleゲームでDenseとLSTMネットワークの効果を比較します。

OpenAIからお借りしたイメージ
https://gym.openai.com/videos/2019-10-21--mqt8Qj1mwo/CartPole-v1/poster.jpg

今回はTensorflowを使って、low-levelカスタマイズもあるので、前回 (Actor-Criticモデル強化学習でブロック崩しを挑戦 https://qiita.com/leolui2013/items/b2c5dbc19be5d025c176) より少し難しくなります。(自動微分と勾配テープ、トレーニングループの詳しい説明はTensorflowのドキュメンテーションにありますのでそちらに参考すると分かりやすいと思います。 https://www.tensorflow.org/guide/autodiff , https://www.tensorflow.org/guide/basic_training_loops )

モデルはA2C (Advantage Actor Critic)で、DenseとLSTMを比較するのでネットワークの構成以外にほとんどの変数が同じです。なぜ比較するかと、一番簡単な強化学習モデルはDenseネットワーク(画像ならCNN)だけど、その学習プロセスは1観察データに対して1予測アクションです。そしてLSTMは1シリーズの観察データを入力できますので、より複雑な問題を解けられると思います。ただしその反面は、1シリーズのデータを学習するために、かかる時間が何倍になると予想されます。

この記事は7月にGithubに投稿した記事に基づいて作成します。
https://github.com/leolui2004/cartpole_model_compare

やり方

強化学習の部分は一番複雑です。分かりやすくしたいのでclassにします。最初はdenseネットワークのコードを紹介します。

import tensorflow as tf
tf.keras.backend.set_floatx('float32')
import numpy as np

discount = 0.97
model_lr = 0.0001 # 学習率

class ActorCriticModel:
    def __init__(self, ActionNumber):
        self.ActionNumber = ActionNumber
        self.model = self.dense_model()
        self.opt = tf.keras.optimizers.Adam(model_lr) # 今回はAdamを使う
    
    # Dense層を構築
    def dense_model(self):
        input = tf.keras.layers.Input((4,))
        layer1 = tf.keras.layers.Dense(128, activation='linear')(input)
        layer2 = tf.keras.layers.Dense(32, activation='linear')(layer1)
        logits = tf.keras.layers.Dense(self.ActionNumber)(layer2) # actor部分
        value = tf.keras.layers.Dense(1)(layer2) # critic部分
        return tf.keras.Model(inputs=[input], outputs=[logits, value])

    # アクションを予測する時logitsだけ必要
    def predict(self, input):
        logits, _ = self.model.predict(input)
        return logits

    # ロス関数を定義    
    def compute_loss(self, done, state_, memory):
        # ゲーム終了していないと観察データ(state)を取得して使う
        if done:
            reward_sum = 0.
        else:
            reward_sum = self.model(tf.convert_to_tensor(state_, dtype=tf.float32))[-1][0]

        # 報酬を加算        
        discounted_rewards = []
        for reward in memory.rewards[::-1]:
            reward_sum = reward + discount * reward_sum
            discounted_rewards.append(reward_sum)
        discounted_rewards.reverse()

        # A2Cのadvantageを考慮して全体ロスを計算
        logits, values = self.model(tf.convert_to_tensor(np.vstack(memory.states), dtype=tf.float32))
        advantage = discounted_rewards - values
        value_loss = advantage ** 2
        
        policy = tf.nn.softmax(logits)
        entropy = tf.nn.softmax_cross_entropy_with_logits(labels=policy, logits=logits)
        
        policy_loss = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=memory.actions[0], logits=logits)
        policy_loss *= tf.stop_gradient(advantage)
        policy_loss -= 0.01 * entropy
        total_loss = tf.reduce_mean((0.5 * value_loss + policy_loss))
        return total_loss
    
    # 勾配テープでトレーニング
    def train(self, done, state_, memory):
        state_ = tf.convert_to_tensor(state_, dtype=tf.float32)
        with tf.GradientTape() as tape:
            loss = self.compute_loss(done, state_, memory)
        grads = tape.gradient(loss, self.model.trainable_variables)
        self.opt.apply_gradients(zip(grads, self.model.trainable_variables))
    

    def action_choose(self, state):
        logits = self.model.predict(state)
        # 予想したlogits(合計1ではない)を確率(合計1)に転換
        probs = np.exp(logits[0][0])/sum(np.exp(logits[0][0]))
        # 確率に基づいてアクションを選ぶ
        action = np.random.choice(self.ActionNumber, p=probs)
        return action

そしてより簡単に途中で観察データを保存、削除するためにMemoryというclassを作成します。

class Memory:
    # 定義
    def __init__(self):
        self.states = []
        self.actions = []
        self.rewards = []
    
    # 保存
    def store(self, state, action, reward):
        self.states.append(state)
        self.actions.append(action)
        self.rewards.append(reward)
    
    # 削除
    def clear(self):
        self.states = []
        self.actions = []
        self.rewards = []

次はゲームプレーの部分です。前回と違った部分は主に最初のランダムアクションがなくなりました。前回説明したことも省略します。

import gym
import matplotlib.pyplot as plt

env = gym.make('CartPole-v0')
episode_limit = 1000
score_avg_freq = 20
score_list = []

# モデルやメモリclassを作成
ACM = ActorCriticModel(2) # CartPoleは左右アクションだけなので2にする
memory = Memory()

for episode in range(episode_limit):
    # 環境を初期化
    state_list, state_next_list, action_list = [], [], []
    score, score_memory, timestep = 0, 0, 0
    memory.clear()
    done = False
    observation = env.reset()
    state = observation
    
    while not done:
        timestep += 1
        # アクションを予測
        action = ACM.action_choose(np.array(state)[np.newaxis, :])
        observation_next, reward, done, info = env.step(action)
        
        state_next = observation_next
        state_list.append(state)
        state_next_list.append(state_next)
        action_list.append(action)
        
        score += reward
        score_memory += reward
        state = state_next
        
        # ゲーム終了もしくは10ステップごとにメモリに保存
        if done or timestep == 10:
            memory.store(np.array(state_list), np.array(action_list), score_memory)
            if score_memory > 8:
                ACM.train(done, np.array(np.array(state_next)[None, :]), memory)
            state_list, state_next_list, action_list = [], [], []
            score_memory, timestep = 0, 0
            memory.clear()
            if done:
                score_list.append(score)
                print('Episode {} Score {}'.format(episode + 1, score))

env.close()

score_avg_list = []
for i in range(1, episode_limit + 1):
    if i < score_avg_freq:
        score_avg_list.append(np.mean(score_list[:]))
    else:
        score_avg_list.append(np.mean(score_list[i - score_avg_freq:i]))
plt.plot(score_avg_list)
plt.show()

最後にLSTMネットワークのコードを書きたいですがほぼ同じなので違った部分だけ書きます。

# Denseネットワークの回数は1000回に対してLSTMの方が遥かに多い
episode_limit = 30000
score_avg_freq = 700

# class定義の部分とネットワークの構成も当然違う
self.model = self.lstm_model()
    
def lstm_model(self):
    input = tf.keras.layers.Input((2, 2))
    # LSTMは基本不安定なので安定させるために3階層と適当なDropoutが必要
    layer1 = tf.keras.layers.LSTM(32, return_sequences=True)(input)
    layer2 = tf.keras.layers.Dropout(0.2)(layer1)
    layer3 = tf.keras.layers.LSTM(64, return_sequences=True)(layer2)
    layer4 = tf.keras.layers.Dropout(0.2)(layer3)
    layer5 = tf.keras.layers.LSTM(128)(layer4)
    layer6 = tf.keras.layers.Dropout(0.2)(layer5)
    layer7 = tf.keras.layers.Dense(64, activation='linear')(layer6)
    layer8 = tf.keras.layers.Dense(32, activation='linear')(layer7)
    layer9 = tf.keras.layers.Dense(16, activation='linear')(layer8)
    logits = tf.keras.layers.Dense(self.ActionNumber)(layer9)
    value = tf.keras.layers.Dense(1)(layer9)
    return tf.keras.Model(inputs=[input], outputs=[logits, value])

# 観察データをシリーズに変換するためにエンコード関数を導入
def encode(a):
    b = [[0,0],[0,0]]
    b[0] = a[0:2]
    b[1] = a[2:]
    return b

state = encode(observation)
state_next = encode(observation_next)

結果

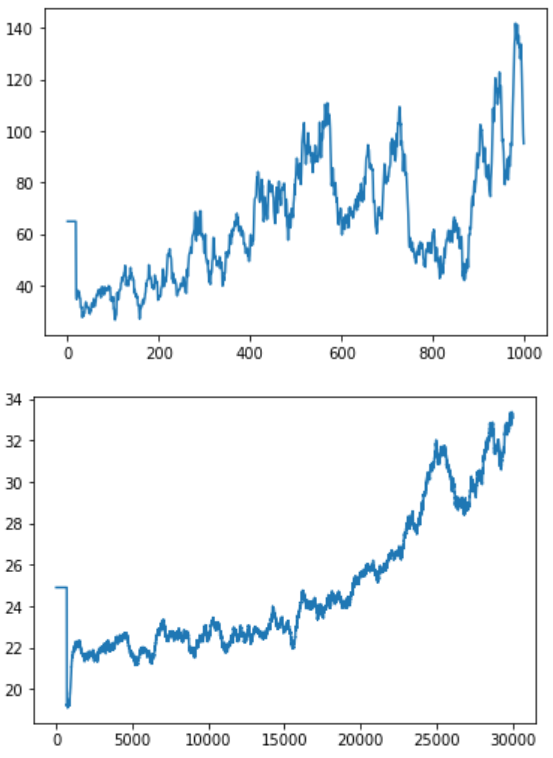
結果はこちらです。1枚目はDense層だけ使いました。2枚目はLSTM層を使いました。X軸訓練回数はDenseの方が1000回、LSTMの方が30000回です。Y軸はスコアです。

結論から言うと、LSTMは学習することが可能です。ただし効果が出るまでにこんなゲームにも10倍以上の訓練回数が必要とみられます。

もう一つ

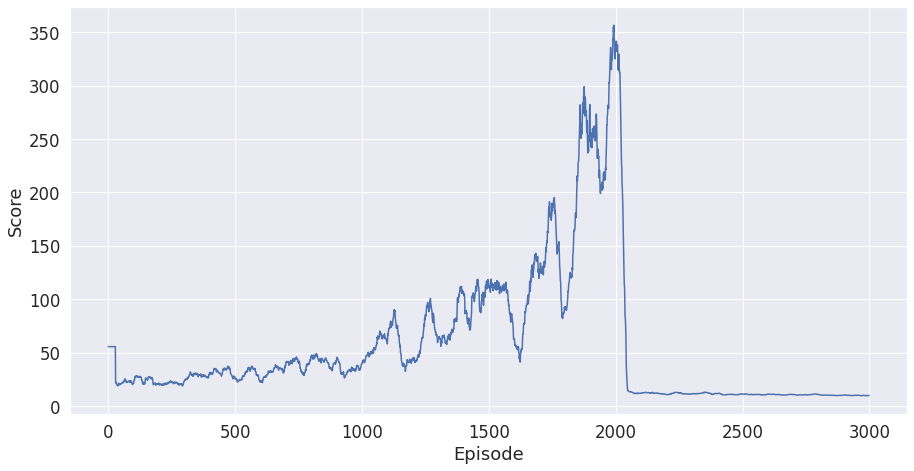
Denseの方を訓練する時この結果が出たことがあります。

これはCatastrophic Forgetting (破滅的忘却?) と言います。実際の理由は不明だけど、途中ですべて学習したことを忘れたら単に訓練回数を上げても解決できないです。この不安定の結果を解消するためにLSTMを推奨すると言われます。