まず回帰分析とは

回帰分析とは何らかの目的変数を別のパラメータ（説明変数）から導き出すモデルを考えることです。
例えばある人の身長は遺伝によりその人の父親の身長と相関があると考えられます。この時息子の身長を「目的変数」として父親の身長から息子の身長を推定することを考えます。
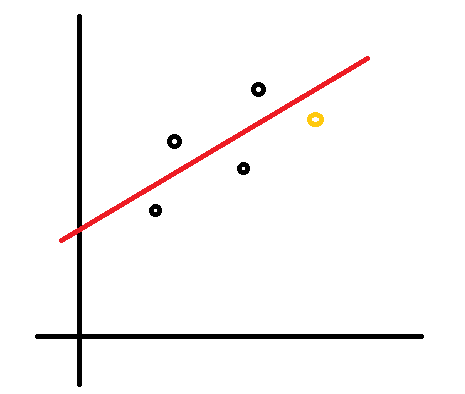
まず、何人もの人の父親の身長(x(i))と息子の身長(y(i))を調べてデータを作ります(x(1),y(1)), x(2),y(2)), x(3),y(3))...)。それをプロットしたところ下図のようになったとします。

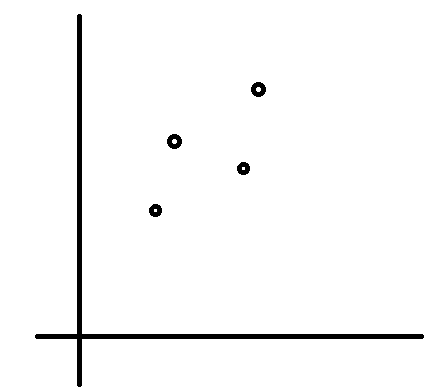
この時、なんとなく以下の直線のような関係があると推測できます。式で書くと$y=ax+b$です。

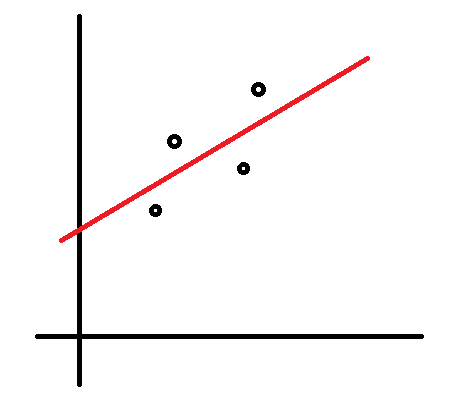
ではどのようなa,bを選ぶのが一番いいのでしょう？それは誤差が一番少なくなるa,bです。具体的には$y=ax+b$で計算したyの値（理論値）と実際のyの値の差（の2乗）の和（ 残差平方和 ）が最小になるa,bです。詳しい計算方法は参考文献¹を見てください。

重回帰分析とは

さて、実際にはある人の身長は父親の身長だけでなく母親の身長や子供の頃何を食べたか、運動したかなどいろいろな要素が影響するでしょう。このような多数の変数から目的変数（この場合は身長）を導き出すモデルを考えることを重回帰分析といいます。
変数が増えても考え方は同じで、 残差平方和 を最小にするような$y=ax_1+bx_2+cx_3+....$を考えることに変わりはありません。幸いJavaにはライブラリがあるので、分析するだけならそれにデータを入れるだけで実現できます。

OLSMultipleLinearRegression regression = new OLSMultipleLinearRegression();
//体重
double[] y = new double[] { 50, 60, 65, 65, 70, 75, 80, 85, 90, 95 };
//身長,ウエスト
double[][] x = new double[10][];
x[0] = new double[] { 165, 65 };
x[1] = new double[] { 170, 68 };
x[2] = new double[] { 172, 70 };
x[3] = new double[] { 175, 65 };
x[4] = new double[] { 170, 80 };
x[5] = new double[] { 172, 85 };
x[6] = new double[] { 183, 78 };
x[7] = new double[] { 187, 79 };
x[8] = new double[] { 180, 95 };
x[9] = new double[] { 185, 97 };
regression.newSampleData(y, x);

Javaでの重回帰分析: Think Statsを読むより引用

回帰分析の問題

非線形関係の場合

さて、今までは暗黙のうちに変数間の関係を線形関係($y=ax+b$)と仮定していました。しかし実際には$y=ax^2$のような関係になっている場合もあると思います。その場合はどうすればいいでしょう。方法の一つは$x^2=:z$と新しい変数を作ることで、これによって$y=az$という線形関係になるのでこれまでの回帰分析の手法が使えます。ただしこの方法は関数形がある程度予想出来ていないと使えません。

過適合の問題

さて、最初以下のグラフに対して直線を当てはめることを考えました。

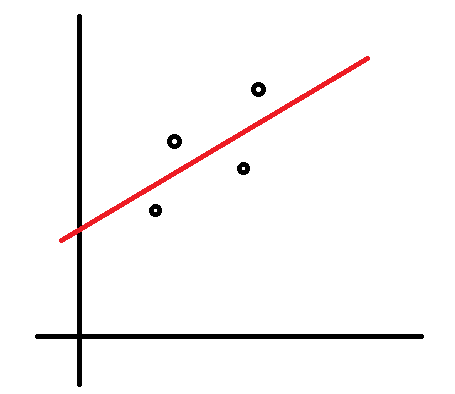
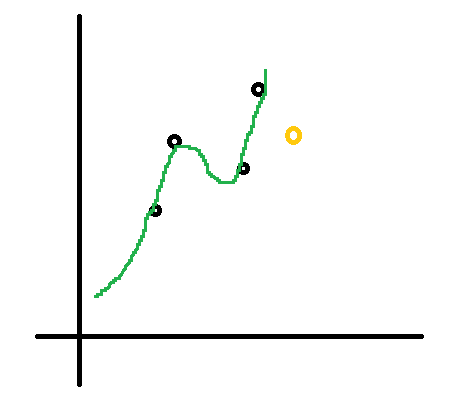
しかし実際には以下の様な複雑な関数を当てはめることも考えられます。

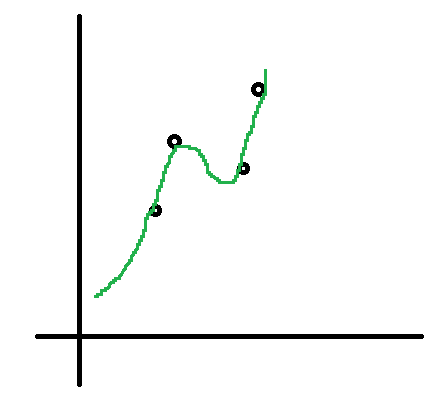
こちらのグラフは完全にデータ点と重なっていて誤差0です。ではこちらの方が良いモデルなのでしょうか？いえ、たしかにこれは 既存の データに対しては誤差が小さいですが未知のデータに対してはかえって予測性能が下がることが考えられます。

これは回帰分析だけでなく機械学習全般に言えることですが、 一般にモデルを複雑にするほど既存のデータにはよく適合するが未知のデータには適合しなくなる 過適合（過学習）という問題があります。

重回帰分析で言えば、変数を増やすほど既存のデータとの誤差は減りますがその分新しいデータに対する予測性能は下がります。かと言って変数を減らしすぎて誤差( 残差平方和 )が大きくなるのもやはり問題です。この両者を考えどの変数を使うべきか考えていかなければいけません。
幸いこれには AIC(赤池情報基準) という指標が存在しており、これが小さいほど良いとされています。

AIC=nlog(SS/n)+2(q+1)(nはデータ数、SSは残差平方和、qは変数の数)

回帰分析の問題のまとめ

結局非線形重回帰分析では次の2つの問題があることがわかります。
1.どの変数を使うべきか
2.使うとして、どのような関数形($x^2,log(x),e^x...$など)を用いるか
以下ではこれを遺伝的アルゴリズムを用いて解くことを考えます。

遺伝的アルゴリズムとは

遺伝的アルゴリズムとは求めたい解を「遺伝子」の形で表し、生物の生存競争を模すことで解を探索する手法のことです。細かい流派や説明はWikipediaをみてもらうこととして、以下では自分のプログラムを具体的な数を出しながら解説していきます。

解の表し方

まず解を遺伝子の形で表す方法を考えます。例えばある変数を使わない場合はUnused、そのままの形で使う場合はLinear、2乗の形で使う場合はSquared, logの場合はLog、というように表すと求めたい式の形が$y=ax_1+cx_3^2+dlog(x_4)(x_2は使わない)$の時、解は「Linear, Unused, Squared, Log」という「遺伝子」で表わされることになります。

個体の生成と「生存競争」

最初にランダムに500体の遺伝子を生成します。それに対して先ほどの AIC を計算し、小さい方から順に並べます。そして上位30体は無条件で生き残らせ、残りは順位が高いほど高い確率で生き残るようにします。これによって「生存者」を決定します。

交配

「生存者」が決定したらそれらからランダムに2体選び「交配」を行います。具体的には「遺伝子」の列から2点を選びその間にある遺伝子を交換します

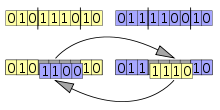
(画像はWikipediaから転載)
これにより「次世代」を作り、個体数が再び500体になるまで繰り返します。

世代交代

再度AICを計算して小さい方から順に並べ替え、最初の「生存競争」に戻りますこれをAICの最良値が変化しなくなるまで行います。

スケール係数

さて、上記では説明をシンプルにするためあえて省きましたが$e^x$などの関数では通常とは異なる問題が生じます。例えばある変数の変化によって目的変数の値が大きく変わるとき、その関数は$e^x$の形になることが予想できますが、ここでもしxの値の範囲が0.001~0.004だと$e^x$がほぼ1になってしまい定数関数と変わらなくなってしまいます。そこで実際には$e^{ax}$の形にしてa=1000などにすればxの変化に応じて目的変数がちゃんと大きく変動するようになります。このようなaを以下ではスケール係数と呼ぶことにします。
スケール係数は以下の様な遺伝的アルゴリズムで決定します。
0. まず変数xの 絶対値 の 中央値 を調べ、xがその値の時ax=1となるようなaを考えます(つまり中央値の逆数)

次にその値の1/10から10倍までの中でランダムに値を決めます
「交配」の際は、もし相手側の遺伝子が同じ関数系（Exp(a)とExp(b))ならそのスケール係数の平均((a+b)/2)と合計(a+b)を持つ次世代を作り出す。

以上の手法により複雑な関数も遺伝的アルゴリズムで探索できるようになります。

ソースコード

以上を行うプログラムをGithubに上げてあるので興味のある方は使用してみてください。
https://github.com/lamrongol/NonlinearRegressionFunctionSelectionByGeneticAlgorithm

留意点

タイトルに「非線形」と書きましたが、実際には$y=ax_1+cx_3^2+dlog(x_4)$のような線形結合を前提としており、例えば

y=ax_1bx_2/dlog(x_3x_4)

のような乗算などを含む式だった場合は推定できません。ただ例えば割り算を含んでいた場合はそれが大きくなるほど値が小さくなることには変わりないので係数をマイナスの大きな数にするなどで近似できる可能性があります。

豊田秀樹『回帰分析入門』（東京書籍） ↩

遺伝的アルゴリズムによる非線形重回帰分析の変数＆関数選択