量子コンピューターがコンピューターである理由

こんにちは｜こんばんは。カエルのアイコンで活動しております @kyamaz です。

本稿は、量子コンピュータ Advent Calendar 2020 の17日目（2020年12月17日）の記事エントリーです。昨年の Advent Calendar 2019 では「徒然草｜量子計算機編｜その１〉」を投稿しました。まるで続編があるかのような記事でしたが、次のポエム記事も投稿することなく一年が経ちました。ただ、この一年で量子コンピューター界隈への期待は色褪せることはなく、相変わらず注目の領域であることは嬉しい限りです。

はじめに

本稿の対象は次のような方を想定しております。

• 量子コンピューターや量子プログラミングに興味がある方

留意事項
本稿では、量子コンピューターの計算機としての特性を扱っており、「量子コンピューターが速いのか？」という問いに対しては扱っておりません。本稿の範囲では、単に計算可能な問題を同じように計算することができる（計算可能性）を扱っており、例え量子コンピューターが古典コンピューターより遅く動作したとしてもよい話題です。

コンピューターとは何か？

私たちの身の回りに"コンピューター"というものが登場してから、私たちの生活にはか欠かせない存在となった今日まで、皆さんのそれぞれのイメージの中で"コンピューター"（という言葉）は進化してきました。この私たちが当たり前のように使っている「コンピューター」とは、どういったものなのでしょうか？その定義はあるのでしょうか？"コンピューター"は、日本語では「電子計算機」や「(自動)計算機」と言われています。「計算する機械」と表記すると、電卓も計算する機械といえそうですが、単なる「電卓」との違いは何でしょうか？「コンピューター」は「プログラム（計算のための手順）」に従って計算するという性質が電卓とは違うようなのですが、その定義は「理論計算機科学」で学問的に明確な定義がされています。しかしながら、一般にはあまり知られていないかもしれません。少し詳しく知るために、理論計算機科学の用語を使って解説してみます。

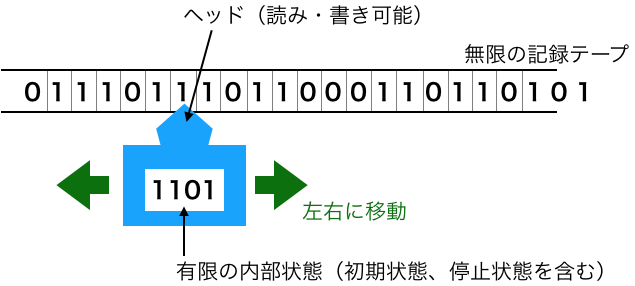
チューリング・マシン

チューリング・マシンとは、計算可能性を示す¹ためにアラン・チューリング氏²により考案された計算モデルです。計算モデルですから、幾つかの前提をおいた思考上のマシンを考えます。次のような特性をもつ部品からなるマシンをチューリング・マシンとします。

• 有限の内部状態（初期状態、停止状態を含む）を持つことができます。
• データを記録する無限の記録テープを備えています。
• １ステップずつ記録テープを左右に移動するヘッドがあり、そのヘッドは記録テープの読み・書きができます。

このチューリング・マシンを動作させるためのプログラムとして「ヘッドが記録テープから読み出したデータと内部状態から、記録テープに書き出すデータ、次の内部状態と次に移動するヘッダの方向決める」という状態遷移を予め準備しておきます。その状態遷移の規則通りにチューリング・マシンを操作すると様々な計算ができます。例えば、$f(x)=x+1$ を計算するために作った状態遷移を使って、それに対応したチューリング・マシンが停止するまで動作させると正しく計算ができます。すなわち、チューリング・マシンというモデルを通して、関数 $f(x)=x+1$ を計算させるチューリング・マシンが作れて、計算可能であることが示せます。

万能チューリング・マシン

ある計算（関数）$f$が与えられたときに、その計算を専用で計算するためのチューリング・マシンは "単能" なもの（その計算しかできない）として定義されています。しかし、"単能"なものを汎用的にすることができます。計算方法である状態遷移を記録テープに納めて、その規則に沿って動作するチューリング・マシンを考えます。このチューリング・マシンは、記録テープに納めた計算規則を変更することで、別の計算を計算することができるようになります。このようなチューリング・マシンを「万能チューリング・マシン」と呼びます。「万能（英語ではUniversal）」とは、単能ではなく、様々な計算（関数）を計算することができるという意味で名付けられています。
理論計算機科学で「コンピューター」とは、万能チューリング・マシンと等価な計算機として定義されます。

ここで挙げたチューリング・マシンは、古典計算に当てはめた計算モデルです。加えて状態遷移が決定的に決まるモデルですので、敢えて明言すると「決定的古典計算」を対象にしています。理論計算機科学では、ほかにも状態遷移が確率的に定義された「確率的古典計算」におけるチューリング・マシンもあり、計算量を扱うための計算モデルや量子計算へ拡張する際に役立つモデルとしても研究されています。

ここまでは抽象的な「コンピューター」の定義について述べてきましたが現実的な古典コンピューター（ここからは従来のコンピューターを量子コンピューターと区別するために"古典コンピューター"と表記します）について考えてみましょう。
古典コンピューターが扱うデータは「０」と「１」のみで表されることは、ご存知だと思います。チューリング・マシンの内部状態や記録テープに記録されたデータ、ヘッドを動かす方向も「０」と「１」のみで表されていると考えても一般性は失われません。
そして、プログラムである状態遷移は、M入力N出力の論理演算の集まりであると考えられます。ひとつの用語を定義しましょう。「M入力N出力のすべての論理演算を、少数の基本論理演算の組合せで表現できる」とき、その基本論理演算の集合を「万能論理演算集合」といいます。｛AND, OR, NOT｝, ｛AND, NOT｝, ｛OR, NOT｝, ｛NAND｝, ｛NOR｝ は全て万能論理演算集合です。例えば｛NAND｝が万能論理演算集合ということは、全ての古典コンピューターのプログラムは NAND 回路だけで記述ができると言っても言い過ぎではないという事になります。

現実的な古典コンピューターは、次の特徴を備えています。

コンピューターが備える特徴

1. 扱うデータの情報は「０」と「１」を表現できる
2. 万能論理演算集合の演算が動作する

そして、理論計算機科学の用語を使うと「万能チューリング・マシンを実現したものがコンピューターである」と言えます。本稿ではこの２つの特徴があれば「コンピューター」であるとしましょう。

量子コンピューターの万能性

“量子コンピューターは、古典コンピューターの上位互換”と言われています。“上位”という言葉を除くと、量子コンピューターは、古典コンピューターと互換性があるということです。上記の２つの"コンピューターが備える特徴"を考えれば、古典コンピューターと互換性が示せます。それぞれについて見てみましょう。

1. 扱うデータの情報は「０」と「１」を表現できる
量子コンピューターで扱う情報は、量子ビットと言います。量子ビットは、$\alpha\lvert 0 \rangle+\beta\lvert 1 \rangle$ $(\alpha,\beta \in C, \vert\alpha\vert^2+\vert\beta\vert^2=1)$ と表現できます。これは１量子ビットがちょうど球の表面上の情報³を表現できることに相当します。２量子ビット⁴になると積状態に加えてエンタングル状態も含まれるため、２つの球面よりも更に情報量が増えた情報を表現できるようになります。
１量子ビットの表現形に $\{\alpha,\beta\}$に$\{1,0\},\{0,1\}$ を代入すると、それぞれ $\lvert 0 \rangle$ と $\lvert 1 \rangle$ となります。これは古典ビットの「０」と「１」に対応づけられますので、量子コンピューターで扱うデータの情報は「０」と「１」を表現できます。⁵

2. 万能論理演算集合の演算が動作する
前述の通り万能量子演算集合は、様々な組み合わせが考えられます。そこで、量子コンピューターで NAND 回路の計算ができることが示せれば、量子コンピューターは万能量子演算集合｛NAND｝の演算ができることになり、古典コンピューターの仲間入りができます。（最低でも古典コンピューターと同等であることが示せます。）
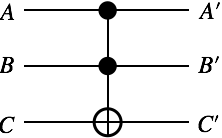
量子コンピューターには量子ビットを演算するための操作が定義されています。一般的な量子演算をユニタリ演算と呼びます。その中で３量子ビットの演算「Toffoli」（“トフォリ”と読みます）をみてみましょう。天下り的ですが、このトフォリ演算が NAND 回路と同等の演算になっていることが、次の真偽値表で確かめられます。

まずは、NANDの真偽値表です。

A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

トフォリ演算の量子回路は下図のような回路です。入力値をA, B, Cとして、出力値をA', B', C'として真偽値表をみます。トフォリ演算は、入力値A, Bがともに１のときに、Cの値が反転して出力される演算です。

トフォリ演算の量子回路図

A	B	C	A'	B'	C'
0	0	0	0	0	0
0	0	1	0	0	1	*
0	1	0	0	1	0
0	1	1	0	1	1	*
1	0	0	1	0	0
1	0	1	1	0	1	*
1	1	0	1	1	1
1	1	1	1	1	0	*

表の右側に ＊ がある行だけを見てください。入力値Cを１に固定（青字）すると、NANDの真偽値表と同じになります。この真偽値表を比べるとわかる通り、トフォリ演算はNANDを含みます。入力C=1を固定できるとすれば、NANDと等価であると言えます。

トフォリ演算を備えた量子計算機は、古典万能計算ができる計算機と言えますので、万能論理演算集合の演算が動作することが示せました。

ここまでで、天下り的に導入したトフォリ演算を備えた量子計算機は「（古典的な）コンピューター」と呼べることがわかりました。

万能量子チューリング・マシン

“量子コンピューターは、古典コンピューターの上位互換”であると言われる“上位”の理由はここまでの説明では分かりません。前述したように、量子ビットの情報は単なる「０」「１」よりも豊富な表現形式ですし、トフォリ演算も真偽値表の入出力だけでは量子ビットによる演算を全て表してはいません。つまり、量子計算を考えるときには、古典計算における計算モデルだけで示せないモデルの導入が必要になりそうです。そこで、万能（古典）チューリング・マシンを内包するように「万能“量子”チューリング・マシン」を計算モデルとして拡張して、量子計算を研究する分野も研究が進んでおります。

その辺りを少しだけ突っ込んでみてみましょう。
古典的に万能論理演算集合を定義しましたが、これを量子計算に拡張して「任意の量子演算が表現できる量子論理演算の集合」を「万能量子論理演算集合」と呼びます。またも天下り的ですが、$N$量子ビット上での量子計算は、１量子ビットに対する任意のユニタリ演算（$^\forall U$ for 1-Qubit）とCNOT演算で表すことができることが分かっています。つまり、量子演算の集合$\{^\forall U$ for 1-Qubit $, CNOT\}$ は「万能量子論理演算集合」です。そして、１量子ビットに対する任意の量子ゲート操作（ユニタリ演算：$^\forall U $ for 1-Qubit）は、アダマールゲート（H） と π / 8 ゲート（T）を使って、任意の精度 $\epsilon $ で近似できることが分かっています。すなわち、任意のユニタリ演算 $U$は、良い精度で H と T の積に分解（表現）できます。すべての$N$量子ビット上での量子計算は、H と T と CNOT の積で"近似的に" 表現できます。言い換えると「量子演算集合$\{H, T, CNOT\}$ は万能量子論理演算集合です」となります。

この説明はニールセン・チャンの教科書『Quantum Computation and Quantum Information』や、@ground0state さんのエントリー「ユニバーサル量子コンピュータの「ユニバーサル」について解説」に詳しい解説があります。@ground0state さんのこのエントリーでは次の３つの手順で「量子演算集合$\{H, T, CNOT\}$ は万能量子論理演算集合」であることが示されています。

万能量子論理演算集合を示すアウトライン

1. すべてのユニタリ演算を、２量子ビットに対するユニタリ演算の積に分解
2. 任意の２量子ビットに対するユニタリ演算を、CNOTゲートと任意の１量子ビット演算に分解
3. 任意の１量子ビット演算を、アダマールゲートと$\pi/8$ゲートに分解（ある精度未満で近似的に）

このアウトラインでの証明では、“量子”計算での万能性を扱うため、任意の１量子ビット演算（任意回転操作）を対象にしています。万能性（Universal）を示すだけであれば、手順２.までが示されればよく、手順3. は別のモチベーションがあります。手順3. については、証明は少し数式を使うため別のエントリー『量子コンピューターの計算精度とSolovay-Kitaevの定理』で解説します。

トフォリ演算をH, T, CNOTのみで表す

“量子”計算での万能性ではなく、“古典”計算での万能性を示すためには、トフォリ演算がアダマールゲート（H）、π / 8 ゲート（T） と CNOT ゲートで表せることを示せればよいです。そのトフォリ演算と等価な量子回路を本稿で取り上げておきましょう。（ただし、この量子回路を導出する方法はここでは扱いません。その計算が等価であることは、Pythonのプログラムで計算して確認します。）

トフォリ演算と等価な量子回路は次のようになります。

この量子回路図で $S = T \cdot T $ です。また、$ T^{\dagger}= T \cdot T \cdot T \cdot T \cdot T \cdot T \cdot T= T^7$ ですので、この量子回路はアダマールゲート（H）、π / 8 ゲート（T） と CNOT ゲートだけで表せています。

それでは、この計算が正しいか SymPy⁶ を使って計算をしてみましょう。計算の都合上、$S, T^{\dagger}$は T ゲートの積にはしないで計算します。

トフォリ演算と等価な量子回路

from sympy import *     # SymPy の基本機能
from sympy.physics.quantum import * # qapplyを含む量子計算のための基本機能
from sympy.physics.quantum.gate import H,S,T,CNOT,OneQubitGate
from sympy.physics.quantum.matrixcache import matrix_cache
matrix_cache.cache_matrix('Tdg',Matrix([[1, 0], [0, exp(-I*pi/4)]]))

class Tdg(OneQubitGate): # T^{\dagger} としては、この演算子を使います。
    gate_name = u'Tdg'
    gate_name_latex = u'T^{\dagger}'
    def get_target_matrix(self, format='sympy'):
        return matrix_cache.get_matrix('Tdg', format)

def Toffoli(q0,q1,q2):   # 上の量子回路を返します。※SymPyでは左右の順番が逆になります。
    return T(q0)*S(q1)*CNOT(q0,q1)*Tdg(q1)*CNOT(q0,q1)\
            *H(q2)*Tdg(q1)*T(q2)*CNOT(q0,q2)*Tdg(q2)*CNOT(q1,q2)\
            *T(q2)*CNOT(q0,q2)*Tdg(q2)*CNOT(q1,q2)*H(q2)

represent(Toffoli(2,1,0), nqubits=3)  # 行列表現を表示します

このrepresentの出力結果は、次のようになります。

Matrix([
[1, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 0, 1, 0]])

この行列は、トフォリ演算の表現（行列）と同じです。つまり、トフォリ演算を H, T, CNOT のみで表すことが示せました。

量子アニーラー

“量子コンピューター”は大きく二つの方式があり、「ゲート方式」と「アニーリング方式」であると一般的に説明されています。本稿でこれまで説明してきた理論計算機科学による定義でいう「コンピューター」と呼んでいるのは「ゲート方式」の量子コンピューターです。一方の「アニーリング方式」の量子コンピューターは、ここまでの説明には該当しないのです。理論計算機科学による厳密な解釈ではアニーリング方式は量子コンピューターとは呼べないために、「量子アニーラー」と呼ぶことも多いです。
ただし、これも用語の定義によります。アニーリング方式の量子計算機も確かに量子的な性質を使った計算をしています。万能チューリング・マシンと等価ではありませんが、量子アニーラーは高度な計算を自動的に計算する計算機であることは間違いありません。ですから、量子コンピューターと呼んでよいでしょうとする意見が多く、実際に最近の国際的な標準化が進んでいますが、アナログな量子計算をする量子アニーラーも、量子コンピューターと呼ぶとされています。

終わりに

最後に、私が思う2020年の量子コンピューター界隈の状況について触れて本稿を締めたいと思います。
一時期の“夢の”量子コンピューターという気運は落ち着いて来ているようです。

そんな中、８月に『AWS Braket』が公開されたことが、今年2020年の大きなトピックではないでしょうか。有償ではありますが、D-Wave, Rigetti, Ion-Q が簡単に利用できるようになりました。量子アニーラーを含む様々なタイプの量子コンピューターを AWS が束ねてクラウド課金モデルを構築したことは、今後のビジネスでの活用を考える上で非常に大きな一歩だと思います。
昨年までは、D-Wave や IBM-Q の量子コンピューター・メーカー（量子コンピューターハードウェアを開発・製造している会社）がクラウドサービスを提供していました。市場を醸成するのための無償提供か、有償利用では D-Waveは月額数十万円〜、IBM-Qはアライアンスや協業のためにそれ相応の研究開発費が必要かを選ぶ状況でした。無償利用では、多くの計算時間も確保できず、量子ビット数などに有償利用と比べると制限があり、せいぜい量子計算の学習でしか使えませんでしたし、有償利用ではがっつり投資する状況でした。この二極化が進みつつあり、年間１００万円前後の研究開発費を使うような（ある意味中途半端(?)な）ビジネス用途では手が届く状況ではなかったと思います。
ここに来て AWS によるクラウド提供により、量子コンピューター利用者側の状況の応じた利用検討ができる環境が整いましたし、量子コンピューター・ベンチャー側(D-Wave, Rigetti, Ion-Q)は課金がしやすくなり収益化が容易になりました。利用者・提供者の双方から参入が促進される可能性が増したと思います。つい最近も量子コンピューター・ベンチャーのSDKの対応が発表されました。

詳しくは、AWSブログ『PennyLane on Braket + フォールトトレラントな量子コンピューティングに向けた進歩 + テンソルネットワークシミュレータ』を参照してください。

今後、量子コンピューター分野に参入する人が増えて、量子コンピューターの利用が促進されることを願っております。

---

（●）（●）
/""　＿＿""＼ @kyamazは、オープンソース・コミュニティ⁷を通じて、皆さんと共に新しい技術に挑戦していきたいと考えております。今後とも引き続き、どうぞ宜しくお願い致します。

May your Christmas wishes come true!
May happy Quantum Computer world has come!

参考資料

• 『オートマトンと計算可能性』（培風館）
• 『チューリングの計算理論入門』（講談社）
• 『Quantum Computation and Quantum Information: 10th Anniversary Edition』（Cambridge University Press）
• 『量子計算理論 量子コンピュータの原理』（森北出版）
• Tameem Albash and Daniel A. Lidar, “Adiabatic quantum computation”（arXiv:1611.04471） --- 量子アニーリングや断熱量子計算の研究成果を整理したレビュー論文
• Ledge.ai『量子コンピュータとは｜古典コンピュータとの違い、実用化の最前線、AIとの関係まで』

---

1. チューリング・マシンを考案したチューリングは、コンピューターでは計算できない計算が存在することを証明しました。例として、チューリングマシンが停止するかどうかを判断する問題「プログラムの停止問題」が計算不可能な問題として有名です。 ↩

2. アラン・チューリング氏を描いた２０１５年公開の映画『イミテーション・ゲーム』や講談社ブルーバックス『チューリングの計算理論入門』が参考になります。 ↩

3. 「ブロッホ球」と呼ばれております。 ↩

4. ２量子ビットの表現は、$\alpha\lvert 00 \rangle+\beta\lvert 01 \rangle + \gamma\lvert 10 \rangle + \delta\lvert 11 \rangle$ $(\alpha,\beta,\gamma,\delta \in C, \vert\alpha\vert^2+\vert\beta\vert^2+\vert\gamma\vert^2+\vert\delta\vert^2=1)$ です。 ↩

5. 本文では、量子ビットの表現できる情報で説明していますが、実際は、量子ビットを取り出す（出力する）際に測定という操作があり、１量子ビットの情報は「０」または「１」に収縮します。例え、内部的な情報の表現力が高い量子ビットで計算されたとしても、出力として得られるのは古典コンピューターが扱う「０」と「１」と同じになります。 ↩

6. 量子計算が扱える Python ライブラリ ↩

7. OpenQLプロジェクトは、量子コンピューターを扱うための様々なライブラリを開発するためのオープンソースプロジェクトです。量子情報、量子コンピューターに興味がある人たちが集うコミュニティを運営しております。詳しくはconnpassのサイトをご覧ください。 ↩