$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
どうもabeTです。この記事は量子コンピュータ #2 Advent Calendar 2018の23日目の記事です。間違い等あればコメントよろしくお願いします。
量子コンピュータ #2 Advent Calendar 2018
https://qiita.com/advent-calendar/2018/quantum2
本家はこちら↓
量子コンピュータ Advent Calendar 2018
https://qiita.com/advent-calendar/2018/quantum
はじめに
量子コンピュータは簡単に言うと、量子力学で説明される物理法則を計算原理に使用したコンピュータです。古典的な計算機のビットに対応するものとして量子ビット(qubit)というものを考え、量子ビットに対しユニタリ演算を実行することで計算をします。1量子ビットは0と1だけでなく、0と1の重ね合わせという状態も取り得ます。ユニタリ演算は重ね合わせ具合を変化させるため、連続的なパラメータを持っています。
ところで、このユニタリ演算を実現する物理操作(レーザの照射など)をどのように実現すればよいでしょうか。量子ビットに対して実行できるユニタリ演算、すなわち物理操作は量子コンピュータの実装方式(ハードウェア)に大きく依存します。実装方式によっては、シンプルなユニタリ演算であっても1対1で対応する物理操作を用意することができない場合があります。そこで、基本的なユニタリ演算を組み合わせて、複雑なユニタリ演算を実現することを考えます。
自然な流れとして、任意のユニタリ演算を実現するために必要な最低限のゲートセットは何か知りたくなります。最低限のゲートセットさえ実装できれば、任意のユニタリ演算が実行でき、どんな量子アルゴリズムも実行できるからです。
実は、あるゲートの組み合わせで、任意のユニタリ演算を任意の精度で近似できることが知られています。この任意のユニタリ演算を任意の精度で近似するために必要な最低限のゲートセットをユニバーサルセットと言います。
※量子コンピュータの演算は有限回しか操作できないので誤差は必ず生じますが、計算結果の読み取りに影響がない程度まで精度を上げれば実用上の問題はないと思われます。
そして、ユニバーサルセットを備えた、どんな量子アルゴリズムも実行できる量子コンピュータをユニバーサル量子コンピュータといいます。
ユニバーサルセットは一意ではありませんが、以下ではスタンダードセットと呼ばれるユニバーサルセットによって、任意のユニタリ演算を近似できることを見ていきます。
スタンダードセットはアダマールゲート、CNOTゲート(制御NOTゲートのこと)、$\pi/8$ゲートで構成されます。
参考
- Michael A. Nielsen, Isaac L. Chuang, "Quantum Computation and Quantum Information: 10th Anniversary Edition", (2010/12/9), Cambridge University Press.
- 小柴 健史,藤井 啓祐,森前 智行,『観測に基づく量子計算』,(2017/2/18),コロナ社
- @YuichiroMinato,(2018年09月16日に更新),『量子エラー訂正メモ』,https://qiita.com/YuichiroMinato/items/ebf08bbe938655cbdcfd
- 『量子スプレマシーとは何か』,(平成29年10月6日),http://tomoyukimorimae.web.fc2.com/q_supremacy.pdf
手順
$n$ qubitsの量子回路を考えます。$d=2^n$とすると、ユニタリ演算は$d\times d$ユニタリ行列で表されます。次の手順で任意のユニタリ行列がユニバーサルセットで再現されることを確かめます。
アウトライン
- ユニタリ演算をtwo-levelユニタリ演算の積に分解
- 任意のtwo-levelユニタリ演算をCNOTゲートとSingle qubit演算に分解
- Single qubit演算をアダマールゲートと$\pi/8$ゲートで任意の精度で近似
ここでtwo-levelユニタリ演算とは高々2つの成分の間でのみ、その作用が自明ではないユニタリ一行列のことです。例えば下記のような行列です。
\begin{pmatrix}
* & * & & \\
* & * & & \\
& & 1 & \\
& & & 1
\end{pmatrix}
, \
\begin{pmatrix}
* & & * & \\
& 1 & & \\
* & & * & \\
& & & 1
\end{pmatrix}
, \
\begin{pmatrix}
* & & & *\\
& 1 & & \\
& & 1 & \\
* & & & *
\end{pmatrix}
.
また、Single qubit演算とは、$n$ qubitsのうち、1qubitにのみ作用する演算のことです。
記法
行列表示の基底はz軸を観測軸に取ります。
\ket{0} = \ket{\uparrow} =
\begin{pmatrix}
1\\
0
\end{pmatrix}
, \
\ket{1} = \ket{\downarrow} =
\begin{pmatrix}
0\\
1
\end{pmatrix}.
テンソル積は次のルールで行列表示します。
\begin{pmatrix}
a\\
b
\end{pmatrix}
\otimes
\begin{pmatrix}
c\\
d
\end{pmatrix}
=
\begin{pmatrix}
ac\\
ad\\
bc\\
bd
\end{pmatrix}
,\
\begin{pmatrix}
a & c\\
b & d
\end{pmatrix}
\otimes
A
=
\begin{pmatrix}
aA & cA\\
bA & dA
\end{pmatrix}
.
パウリ行列は次のよう書きます。
X = \sigma_x
=
\begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix} ,\\
Y = \sigma_y
=
\begin{pmatrix}
0 & -i\\
i & 0
\end{pmatrix} ,\\
Z = \sigma_z
=
\begin{pmatrix}
1 & 0\\
0 & -1
\end{pmatrix} .\\
アダマールゲート$H$と$\pi/8$ゲート$T$は次の行列で書けます。
H = \frac{1}{\sqrt2}(X+Z) =\frac{1}{\sqrt2}
\begin{pmatrix}
1 & 1\\
1 & -1
\end{pmatrix}, \\
T = \begin{pmatrix}
1 & \\
& e^{i\frac{\pi}{4}}
\end{pmatrix}
=
e^{i\frac{\pi}{8}}
\begin{pmatrix}
e^{-i\frac{\pi}{8}} & \\
& e^{i\frac{\pi}{8}}
\end{pmatrix}
.
さらに、単位ベクトル$\hat{\bf{n}}$まわりの$\mathrm{SU}(2)$演算を次のように書きます。
R_{\hat{\boldsymbol{n}}}(\theta)
= \exp(-i\frac{\theta}{2}\boldsymbol{n}\cdot \boldsymbol{\sigma})
= I\cdot \cos\frac{\theta}{2}-i(\boldsymbol{n}\cdot \boldsymbol{\sigma})\sin\frac{\theta}{2}.
1. ユニタリ演算をtwo-levelユニタリ演算の積に分解
$3\times 3$行列の例を通して手順を確認します。ユニタリ演算を次のように書きます。
U =
\begin{pmatrix}
a & d & g\\
b & e & h\\
c & f & j
\end{pmatrix}
.
これをtwo-levelユニタリ演算$U_1, U_2, U_3$を用いて$U_3 U_2 U_1 U = I \Leftrightarrow U = U_1^{\dagger} U_2^{\dagger} U_3^{\dagger}$とできることを見ます。
$U_1$について、$b=0$ならば単位行列、$b\neq 0$ならば次の行列にとります。
U_1 =
\begin{pmatrix}
\frac{a^\ast}{\sqrt{|a|^2+|b|^2}} & \frac{b^\ast}{\sqrt{|a|^2+|b|^2}} & 0\\
\frac{b}{\sqrt{|a|^2+|b|^2}} & \frac{-a}{\sqrt{|a|^2+|b|^2}} & 0\\
0 & 0 & 1
\end{pmatrix}
.
すると、2行1列目の成分をゼロにできます。
U_1 U =
\begin{pmatrix}
a' & d' & g' \\
0 & e' & h' \\
c' & f' & j'
\end{pmatrix}
.
$U_2$について、$c'=0$ならば、
U_2 =
\begin{pmatrix}
a'^\ast & & \\
& 1 & \\
& & 1
\end{pmatrix},
$c'\neq 0$ならば
U_2 =
\begin{pmatrix}
\frac{a'^\ast}{\sqrt{|a'|^2+|c'|^2}} & 0 & \frac{c'^\ast}{\sqrt{|a'|^2+|c'|^2}} \\
0 & 1 & 0 \\
\frac{c'}{\sqrt{|a'|^2+|c'|^2}} & 0 & \frac{-a'}{\sqrt{|a'|^2+|c'|^2}}
\end{pmatrix}
,
となります。すると、3行1列目の成分をゼロにできます。$U_2 U_1 U$はユニタリ行列なので、1行2列目と1行3列目もゼロと分かります。
また、$U_2 U_1 U$はユニタリ行列なので、1行目のノルムが$1$となります。したがって1行1列目の成分は$1$となります。
U_2 U_1 U =
\begin{pmatrix}
1 & 0 & 0 \\
0 & e'' & h'' \\
0 & f'' & j''
\end{pmatrix}
.
最後に$U_3$を次のようにとれば良いとわかります。
U_3 =
\begin{pmatrix}
1 & 0 & 0 \\
0 & e''^\ast & f''^\ast \\
0 & h''^\ast & j''^\ast
\end{pmatrix}
.
以上でtwo-levelユニタリ演算に分解できることがわかりました。
$4\times 4$行列の場合でも同様の手順で、3回の操作で、1列目の値を$0$にしていきます。
U =
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & f & k & p\\
0 & g & l & q\\
0 & h & m & r
\end{pmatrix}
,
あとは$3\times 3$の部分行列なので、$3\times 3$のとき全く同じで、$U_1$を部分行列にもつ次の行列、
U'_1 =
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & & & \\
0 & & \LARGE{U_1} & \\
0 & & &
\end{pmatrix}
,
を使って同じ操作をしていけば良いことがわかります。
結局$d\times d$行列の時もtwo-levelユニタリ演算で$U=U_1U_2\cdots U_k$と分解できます。分解に必要な$k$は最大で$(d-1)+(d-2)+\cdots +1 = d(d-1)/2$となることがわかります。
2. 任意のtwo-levelユニタリ演算をCNOTゲートとSingle qubit演算に分解
two-levelユニタリ演算を1qubitのみに作用するSingle qubit演算とCNOTゲート演算の積で表します。つまり、行列演算をテンソル演算にします。
具体例として2qubitsの場合について考えてみます。次のtwo-levelユニタリ演算を考えます。
U =
\begin{pmatrix}
a & & & c\\
& 1 & & \\
& & 1 & \\
b & & & d
\end{pmatrix}
.
これは列ベクトルの1成分目と4成分目にnon-trivialに作用します。今、2qubitの基底は、
\ket{00} =
\begin{pmatrix}
1\\
0\\
0\\
0
\end{pmatrix}
, \
\ket{11} =
\begin{pmatrix}
0\\
0\\
0\\
1
\end{pmatrix}
,
なので、ユニタリ演算は$\ket{00},\ket{11}$のみに作用することがわかります。このことから、CNOTゲートを用いて$\ket{00},\ket{11}$のみに非自明な成分、
\tilde{U} =
\begin{pmatrix}
a & c \\
b & d
\end{pmatrix}
,
を作用できればよいのだろうと考えられます。
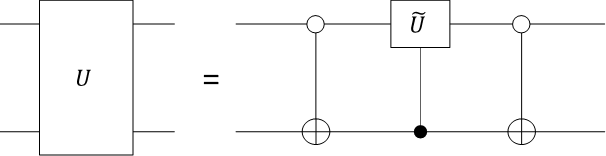
実は、次の手順で上記を実現できることが知られています。
今の場合非自明に作用する基底は00と11です。この二つの数値列の片方からもう片方へ、1回につき1つの数値をフリップしてたどり着くシーケンスを考えます。
00\\
01\\
11.
このシーケンスを量子回路で表現します。ただし、最後のフリップ$01\rightarrow 11$は実施しません。最後と一つ手前の数値列を見て、値が異なるビットを標的として$\tilde{U}$の制御ユニタリゲートを作用させます。つまり、1ビット目以外をソースとして、1ビット目をターゲットとする$\tilde{U}$の制御ユニタリゲートを作用させます。その後、フリップを元に戻す演算をします。図にすると次のようになります。
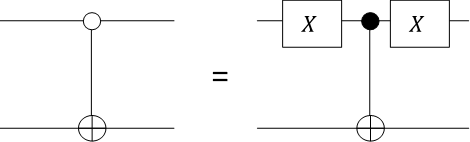
ここで、左から一つ目のゲートは名前がついていませんが、ここでは否定CNOTゲートと呼ぶことにします。否定CNOTゲートは次の図で表されるゲートです。
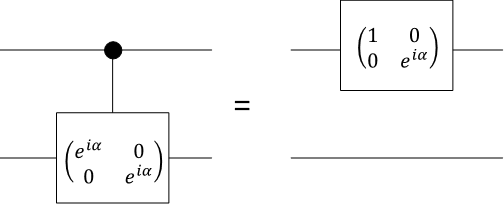
制御ユニタリ演算ですが、任意のSingle qubit演算は$ABC=I$を満たすユニタリ行列$A,B,C$を用いて$U=e^{i\alpha}AXBXC$と書けることから、$e^{i\alpha}$と$X$を制御演算にすれば$U$にできることがわかります。
制御位相シフトゲートはSingle qubit演算で書き直せます。
結局、制御ユニタリゲートもCNOTゲートとSingle qubit演算で書けることがわかりました。(この制御ユニタリゲートについてはEMANさんのサイトに解説があります。詳しくはそちらをご参照下さい。)
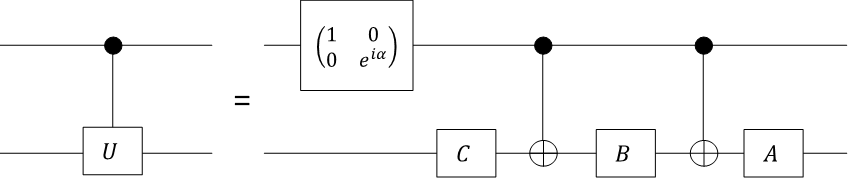
話を戻して、$U$をCNOTゲートと$\tilde{U}$の積に分解できているか確認します。否定制御ゲートは行列で書くと次のように書けます。
\begin{pmatrix}
0 & 1 & & \\
1 & 0 & & \\
& & 1 & \\
& & & 1
\end{pmatrix}
.
制御ユニタリゲートは、
\begin{align}
I\otimes\ket{0}\bra{0} + \tilde{U}\otimes \ket{1}\bra{1}
&=
\begin{pmatrix}
1 & \\
& 1
\end{pmatrix}
\otimes
\begin{pmatrix}
1 & \\
& 0
\end{pmatrix}
+
\begin{pmatrix}
a & c \\
b & d
\end{pmatrix}
\otimes
\begin{pmatrix}
0 & \\
& 1
\end{pmatrix}
\\
& =
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & a & 0 & c\\
0 & 0 & 1 & 0\\
0 & b & 0 & d
\end{pmatrix}
\end{align}
,
となります。これらから計算すると次のようになります。
\begin{pmatrix}
0 & 1 & & \\
1 & 0 & & \\
& & 1 & \\
& & & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & a & 0 & c\\
0 & 0 & 1 & 0\\
0 & b & 0 & d
\end{pmatrix}
\begin{pmatrix}
0 & 1 & & \\
1 & 0 & & \\
& & 1 & \\
& & & 1
\end{pmatrix}
=
\begin{pmatrix}
a & & & c\\
& 1 & & \\
& & 1 & \\
b & & & d
\end{pmatrix}
.
確かに$U$になっていることがわかります。よってCNOTゲートとSingle qubit演算で2qubitのtwo-levelユニタリ演算が書けることがわかりました。
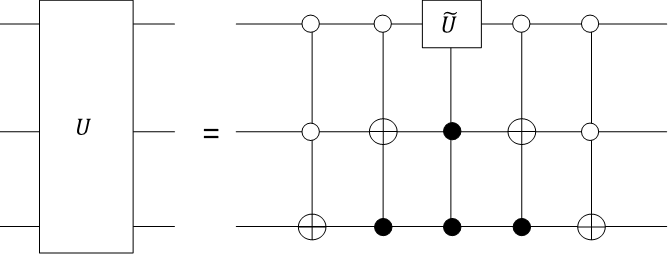
3qubits以上でも同様の手順で計算できます。例えば3qubitsの場合で、
U =
\begin{pmatrix}
a & & & & & & & c\\
& 1 & & \\
& & 1 & \\
& & & 1 & \\
& & & & 1 &\\
& & & & & 1 & \\
& & & & & & 1\\
b & & & & & & & d
\end{pmatrix}
,
two-levelユニタリ演算の時はシーケンスは、
000\\
001\\
011\\
111,
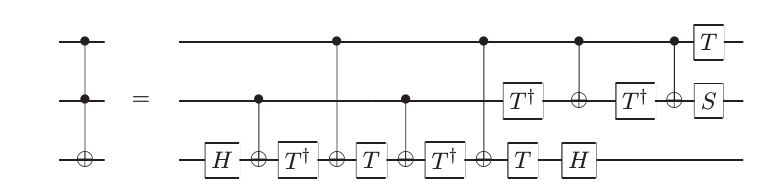
トフォリゲートもCNOTゲートとSingle qubit演算で表せます。
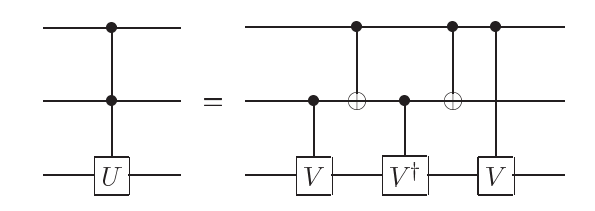
制御・制御Uゲートもです。$U=V^2$として、次の図になります。
同様にして$n$qubitsのときもCNOTゲートとSingle qubit演算でtwo-levelユニタリ演算を表すことができます。
3. Single qubit演算をアダマールゲートと$\pi/8$ゲートで任意の精度で近似
1と2の結果を合わせると、任意のユニタリ演算をCNOTゲートとSingle qubit演算で表すことができました。ここまでは近似を使っていないので、厳密に正しいです。
あとは、Single qubit演算をアダマールゲート$H$と$\pi/8$ゲート$T$で近似できれば良いことになります。ユニタリ行列$U$をユニタリ行列$V$で近似できるとは、ユニタリ行列に入れた次の距離が任意に小さくできることを言います。
E(U,V) = \mathrm{max}_\psi||(U-V)\ket{\psi}||
= 2-\mathrm{max}_\psi\bra{\psi}(U^\dagger V + V^\dagger U )\ket{\psi}.
$\mathrm{max}_\psi$は規格化された状態$\psi$すべてのうち、引数が最大になるものを取るという意味です。
まず、$T$はz軸周りの回転、$HTH$はx軸周りの回転に対応することを見ます。
\begin{align}
R_z(\frac{\pi}{4}) &= \exp(-i\frac{\pi}{8}\sigma_z) =
\begin{pmatrix}
e^{-i\frac{\pi}{8}} & 0 \\
0 & e^{i\frac{\pi}{8}}
\end{pmatrix}
=
e^{-i\frac{\pi}{8}} T \\
R_x(\frac{\pi}{4}) &= \exp(-i\frac{\pi}{8}\sigma_x) =
\begin{pmatrix}
\cos\frac{\pi}{8} & -i\sin\frac{\pi}{8} \\
-i\sin\frac{\pi}{8} & \cos\frac{\pi}{8}
\end{pmatrix}
=
e^{-i\frac{\pi}{8}} HTH \\
\end{align}
これらの積を考えます。
\begin{align}
e^{-i\frac{\pi}{4}} THTH
&= \exp(-i\frac{\pi}{8}\sigma_z)\exp(-i\frac{\pi}{8}\sigma_x)\\
&= I\cdot \cos^2\frac{\pi}{8} - i\left[ \frac{\cos\frac{\pi}{8}}{\sqrt{1+\cos^2\frac{\pi}{8}}}(X+Z)+\frac{\sin\frac{\pi}{8}}{\sqrt{1+\cos^2\frac{\pi}{8}}} \right]\sqrt{1-\cos^4\frac{\pi}{8}}
\end{align}
これは、$\hat{\boldsymbol{n}}=\frac{1}{\sqrt{1+\cos^2\frac{\pi}{8}}}(\cos\frac{\pi}{8},\sin\frac{\pi}{8},\cos\frac{\pi}{8})$周りの$\cos\frac{\theta}{2}=\cos^2\frac{\pi}{8}$を満たす$\theta$回転になっています。
この演算を繰り返すことで、$\hat{\boldsymbol{n}}$周りの任意の回転$R_{\hat{\boldsymbol{n}}}(\alpha)$を近似できることを示します。任意の精度$\delta>0$を決めます。$N$は$N>2\pi/\delta$を満たすとします。$\theta_k(k=1,...N)$を$\theta_k\in[0,2\pi),\theta_k=k\theta \ \mathrm{mod} \ 2\pi$とします。$\theta$は$\pi$の倍数でないので、$k\neq j$であれば$\theta_k-\theta_j \neq 0$です。鳩の巣原理により、$|\theta_k-\theta_j|\leq 2\pi/N<\delta$が成り立つ$j,k$が存在します。一般性を失わずに$k>j$と出来て、$|\theta_{k-j}|<\delta$となります。様々な$\ell$で、$\theta_{\ell(k-j)}$を考えることで、$[0,2\pi)$を満たすことができます。隣り合う角度との差分は$\delta$よりも小さくなります。
以上の結果を用いて$\alpha$を近似します。$\theta_0=\ell_0(k-j)\theta \ \mathrm{mod} \ 2\pi$の$\ell_0$を$|\alpha-\theta_0|=\varepsilon<\delta$を満たすものとします。すると、次に示すように、任意の精度で$R_{\hat{\boldsymbol{n}}}(\alpha)$を近似することができます。
E(R_{\hat{\boldsymbol{n}}}(\alpha),R_{\hat{\boldsymbol{n}}}(\theta_0))
=E(R_{\hat{\boldsymbol{n}}}(\alpha),R_{\hat{\boldsymbol{n}}}(\theta)^{\ell_0(k-j)})
=2(1-\cos\frac{\varepsilon}{2})<2\varepsilon,
これで同一の単位ベクトルを持つ角度違いの演算子を近似することができました。
さらに簡単な計算で、
HR_{\hat{\boldsymbol{n}}}(\alpha)H = R_{\hat{\boldsymbol{m}}}(\alpha),
$\hat{\boldsymbol{m}}=\frac{1}{\sqrt{1+\cos^2\frac{\pi}{8}}}(\cos\frac{\pi}{8},-\sin\frac{\pi}{8},\cos\frac{\pi}{8})$となることがわかります。$\hat{\boldsymbol{n}}$と$\hat{\boldsymbol{m}}$は1次独立なので、Single qubit演算$U$を次のように分解できます。
U = e^{i\tau}R_{\hat{\boldsymbol{n}}}(\beta)R_{\hat{\boldsymbol{m}}}(\gamma)R_{\hat{\boldsymbol{n}}}(\eta)
これと先ほどの結果を合わせると、結局次のようになります。
E(U,R_{\hat{\boldsymbol{n}}}(\theta)^{n_1}HR_{\hat{\boldsymbol{m}}}(\theta)^{n_2}HR_{\hat{\boldsymbol{n}}}(\theta)^{n_3})
<\varepsilon,
ここで、全体にかかる位相因子は無視しました。
以上から、Single qubit演算をアダマールゲート$H$と$\pi/8$ゲート$T$で任意の精度で近似できることがわかりました。
よって、アダマールゲート、CNOTゲート、$\pi/8$ゲートの組がユニバーサルセットであることを確かめることができました。
補足
制御制御Uゲートのところでサラッと任意のユニタリ行列$U$に対し$U=V^2$なる$V$を使用していましたが、この$V$の構成は自明ではありません。$U$がSU(2)の行列$R_{\hat{\boldsymbol{n}}}(\theta) $であれば、$V$は$R_{\hat{\boldsymbol{n}}}(\theta/2) $とすればよいです。一般のU(2)行列、
\begin{align}
\begin{pmatrix}
e^{ia}\cos \theta & e^{ic} \sin \theta\\
e^{ib} \sin \theta & e^{id} \cos \theta
\end{pmatrix},
\end{align}
に対しては簡単に$V$を作ることはできません。
ただし、ユニバーサル量子コンピュータの話に限れば、Single qubit演算をSU(2)行列と位相行列の積で近似しているので、これは$V$を求めることができます。
おわりに
本稿では量子コンピュータの「ユニバーサル」について見てきました。アダマールゲート、CNOTゲート、$\pi/8$ゲートの組があれば、任意のユニタリ演算を任意の精度で近似できることがわかりました。
ところで、CNOTゲートおよびSingle qubit演算が合わせてm個ある回路を$\varepsilon$の精度で、ユニバーサルゲートのみで実現しようとするとどれくらいのゲートが必要になるでしょうか。これは、Solovay-Kitaevの定理によると、$\mathcal O(m\log^c(m/\varepsilon))$で済むことがわかっています。
しかし、現在の量子コンピュータはエラー訂正が未実装のため、ゲートの数が多くなるほどノイズが倍増され、正しい結果を得ることが難しくなります。そこで、ユニバーサルでなくてもよいので、何か古典コンピュータよりも優れているということを証明することができないだろうか、という理論的研究が量子スプレマシーです。
次回は量子スプレマシーについて書けるといいな、といったところで終わりにしたいと思います。ここまで読んでいただきありがとうございました。