こんにちは|こんばんは。カエルのアイコンで活動しております @kyamaz ![]() 1 です。
1 です。
本稿では、ゲート方式の量子コンピューターについてのみ扱います。量子コンピュータ Advent Calendar 2020 の17日目(2020年12月17日)の投稿「量子コンピューターがコンピューターである理由」に関連した投稿です。
はじめに
本稿の対象は次のような方を想定しております。
- 量子コンピューターや量子プログラミングに興味がある方
- (少し数式がでてきますので)数式があっても平気な方
任意の1量子ビット演算の近似的な分解
@ground0state さんのエントリー「ユニバーサル量子コンピュータの「ユニバーサル」について解説」で「量子演算集合$\{H, T, CNOT\}$ は万能量子論理演算集合」であることが示されています。@ground0state さんのエントリーでは次の3つの手順で説明されています。
万能量子論理演算集合を示すアウトライン
- すべてのユニタリ演算を2量子ビットに対するユニタリ演算の積に分解
- 任意の2量子ビットに対するユニタリ演算をCNOTゲートと任意の1量子ビット演算に分解
- 任意の1量子ビット演算をアダマールゲートと$\pi/8$ゲートに分解(ある精度未満で近似的に)
本稿では、この中から「任意の1量子ビット演算をアダマールゲートと$\pi/8$ゲートに分解(ある精度未満で近似的に)」にフォーカスして解説します。
量子状態は壊れやすい
万能性(Universal)を示すだけであれば、手順2. までが示されればよく、手順3. は別のモチベーションで示される必要があります。それでは、なぜアダマールゲートと$\pi/8$ゲートだけで表すことを示したいのでしょうか?しかも手順3. では近似的に等しいということを示しています。(近似的といっても、限りなく誤差を小さくできるということを示していますので、等しいと呼べる程度には正確な話しではあります。)
繊細な量子計算を精密に実行するには、物理的な制御に限界があります。精密な量子計算には2つの制御的な課題があります。1つめは、量子コンピューターの情報単位である量子ビットが量子性を保つ時間(コヒーレンス時間といいます)は長くなく、量子ビットが期待どおりに量子的な情報を保持し続けることを前提とすることはできません。もう1つは、1量子ビットに対する演算は任意のユニタリ演算ができることを期待しますが、例えば超電導型の量子コンピューターでは、その演算操作は物理的には電磁波(マイクロ波)の照射時間を厳密に調整しなければならず、期待通りの演算することは困難です。任意のユニタリ演算を行うのは、超電導型に限らずどのような物理実装でもノイズによる影響が少なからずあります。
そこで、この量子ビットに対する不安定さと、量子演算に対する不安定さを前提に、量子計算を精密にしていく機構とその論理が必要になります。この理論的な裏付けを研究している分野が「量子誤り訂正」と呼ばれています。
深入りしませんが、CNOTゲート(CX), Hadamardゲート(H), 位相ゲート(S), π/8ゲート(T) の量子演算のセットだけを使えば、誤り制御をしつつ、量子計算を継続できることが示されています。パウリ演算(Xゲート、Yゲート、Zゲート)も量子誤り訂正には必要で、これらとともに誤り耐性を考えるのですが、誤り訂正をし続けるために、ここで挙げた量子ゲートだけで任意の量子計算を翻訳することが求められます。次からは「任意の1量子ビット演算をHゲートとπ/8ゲートで表す」ことを解説します。
任意の1量子ビット演算をHゲートとπ/8ゲートで近似する
まず、$T$ゲート演算と、$H$ゲートと$T$ゲートの積 $HTH$ を考えます。$T$ゲート演算は、次のように $\exp$の中に $ \sigma_z $ が入った形式で表現できます。これは$z$軸周りの回転操作2であることを表しています。
$\begin{equation}\left.\begin{aligned}
T = e^{i \pi/8} \begin{pmatrix}
e^{- i \pi/8} & 0 \\ 0 & e^{i \pi/8}
\end{pmatrix}
= e^{i \pi/8} \cdot \exp {\left( -i \frac{\pi}{8} \sigma_z \right)}
\end{aligned} \right. \end{equation}$
積 $HTH$ の計算は次のような計算で、この積は$x$軸周りの回転操作であることが示せます。
$\begin{equation} \left.\begin{aligned}
HTH &= \frac{1}{\sqrt{2}} \left( \begin{matrix}
1 & 1 \\ 1 & -1
\end{matrix} \right)
e^{i \pi/8} \left( \begin{matrix}
e^{- i \pi/8} & 0 \\ 0 & e^{i \pi/8}
\end{matrix} \right)
\frac{1}{\sqrt{2}} \left( \begin{matrix}
1 & 1 \\ 1 & -1
\end{matrix} \right) \
&= \frac{e^{i \pi/8}}{2} \left( \begin{matrix}
e^{i \pi/8}+e^{-i \pi/8} & -(e^{i \pi/8}-e^{-i \pi/8}) \\ -(e^{i \pi/8}-e^{-i \pi/8}) & e^{i \pi/8}+e^{-i \pi/8}
\end{matrix} \right) \
&= e^{i \pi/8} \left( \begin{matrix}
\cos(\pi/8) & -i \sin(\pi/8) \\ -i \sin(\pi/8) & \cos (\pi/8)
\end{matrix} \right) \
&= e^{i \pi/8} \cdot \exp {\left( -i \frac{\pi}{8} \sigma_x \right)} \
\end{aligned} \right. \end{equation}$
そして次に $T \cdot HTH$ と $HTH \cdot T$ を計算して、それぞれについて考えます。
$ \begin{equation}\left.\begin{aligned}
T \cdot HTH &= e^{i \pi/4} \cdot \exp {\left( -i \frac{\pi}{8} \sigma_z \right)} \exp {\left( -i \frac{\pi}{8} \sigma_x \right)} \
&= e^{i \pi/4} \left( \cos \frac{\pi}{8}I - i \sin \frac{\pi}{8} \sigma_z \right) \left( \cos \frac{\pi}{8}I - i \sin \frac{\pi}{8} \sigma_x \right) \
&= e^{i \pi/4} \{ \underset{回転角\ \theta}{\underline{\cos^2 \frac{\pi}{8} }} I - i \sin \frac{\pi}{8} \underset{回転軸\ \vec{n}}{\underline{ \left( \cos \frac{\pi}{8} \sigma_x + \sin \frac{\pi}{8} \sigma_y + \cos \frac{\pi}{8} \sigma_z \right) }} \} \
\end{aligned} \right. \end{equation} $
$T \cdot HTH$は、回転軸を $\vec{n} = \left( 1, \tan{\frac{\pi}{8}} ,1 \right) $ とし、回転角を $\theta = 2 \arccos{\left( \frac{2+\sqrt{2}}{4} \right)} $ とした回転操作($R_{\vec{n}} \left( \theta \right)$とおく)となります。
$ \begin{equation}\left.\begin{aligned}
HTH \cdot T &= H \cdot THT \cdot H \cdot H = H \cdot R_{\vec{n}} \left( \phi \right) \cdot H \
&= e^{i \pi/4} \{ \underset{回転角\ \theta}{\underline{\cos^2 \frac{\pi}{8} }} I - i \sin \frac{\pi}{8} \underset{回転軸\ \vec{m}}{\underline{ \left( \cos \frac{\pi}{8} \sigma_x - \sin \frac{\pi}{8} \sigma_y + \cos \frac{\pi}{8} \sigma_z \right) }} \} \
\end{aligned} \right. \end{equation} $
$HTH \cdot T$は、回転軸を $\vec{m} = \left( 1, - \tan{\frac{\pi}{8}} ,1 \right) $ とし、回転角を $\theta$ とした回転操作($R_{\vec{m}} \left( \theta \right)$とおく)となります。
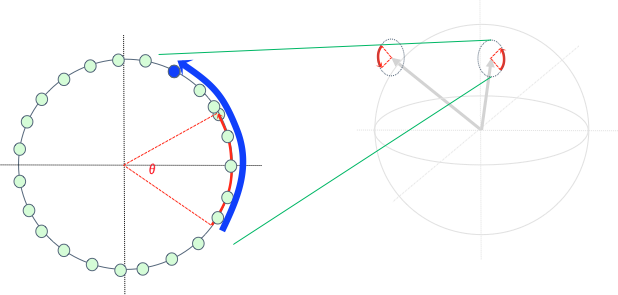
ここで、任意角$\alpha$の回転操作 $R_n \left( \alpha \right) $ を考えるとき、任意の $\varepsilon_{n} \left( \alpha \right) $ に対して、次式を満たす $k_n \left( \alpha \right) $ が存在します。ここで$E()$は演算の誤差です。3
$E\left( R_{n}\left( \alpha \right), R_{n}\left( k_n \left( \alpha \right) \cdot \theta \right)\right) \lt \varepsilon_{n} \left( \alpha \right)$
この式の意味するところは、目的の回転操作$\alpha$に対して $\theta$のある定数倍 $k_n \left( \alpha \right)$の回転操作は、誤差 $\varepsilon_{n} \left( \alpha \right)$ より小さくできるということです。つまり、誤差 $\varepsilon_{n} \left( \alpha \right)$ を限りなく0に近づけたとしても、それより小さくできる $\alpha$ に近い $\theta$の整数倍の角度が存在するということになります。
これには、単位回転角となる $\theta$ が無理数であることや、数学的な稠密の概念が関係しています。
上記は、回転軸 $\vec{n}$ に対しての近似と考えてみましょう。そして、同じ式の記号を変えた式ですが、回転軸を $\vec{m} $ に対しての近似が次式となります。
$E\left( R_{m}\left( \beta \right), R_{m}\left( k_m \left( \beta \right) \cdot \theta \right)\right) \lt \varepsilon_{m} \left( \beta \right)$
さて、いま示したい任意の1量子ビット演算のユニタリ$U$は、グローバル位相を除いて、
$ \begin{equation}\left.\begin{aligned}
U = R_n \left( \alpha_{1} \right) R_m \left( \beta_{1} \right)
R_n \left( \alpha_{2} \right) R_m \left( \beta_{2} \right)
\dots R_n \left( \alpha_{N/2} \right) R_m \left( \beta_{N/2} \right)
\end{aligned} \right. \end{equation} $
のように近似的に表せます。これを $T \cdot HTH$ と $HTH \cdot T$ を組み合わせて表してみると、次のようになります。
$ \begin{equation}\left.\begin{aligned}
U &\simeq (T \cdot HTH)^{k_1(\alpha_1)} (HTH \cdot T)^{k_1(\beta_1)}
\cdot R_n \left( \alpha_{2} \right) R_m \left( \beta_{2} \right)
\dots R_n \left( \alpha_{N/2} \right) R_m \left( \beta_{N/2} \right) \
&\simeq (T \cdot HTH)^{k_1(\alpha_1)} (HTH \cdot T)^{k_1(\beta_1)}
(T \cdot HTH)^{k_2(\alpha_2)} (HTH \cdot T)^{k_2(\beta_2)}
\dots R_n \left( \alpha_{N/2} \right) R_m \left( \beta_{N/2} \right) \
&\simeq (T \cdot HTH)^{k_1(\alpha_1)} (HTH \cdot T)^{k_1(\beta_1)}
(T \cdot HTH)^{k_2(\alpha_2)} (HTH \cdot T)^{k_2(\beta_2)}
\dots (T \cdot HTH)^{k_{N/2}(\alpha_{N/2})} (HTH \cdot T)^{k_{N/2}(\beta_{N/2})} \
&\simeq (T \cdot HTH)^{k_1} (HTH \cdot T)^{k_2}
(T \cdot HTH)^{k_3} (HTH \cdot T)^{k_4}
\dots (T \cdot HTH)^{k_{N-1}} (HTH \cdot T)^{k_{N}}
\end{aligned} \right. \end{equation} $
そしてこの誤差は、すべての誤差の最大値を $\varepsilon_{N}$ とすると、
$E\left( U, R_n \left( \alpha_{1} \right) R_m \left( \beta_{1} \right)
R_n \left( \alpha_{2} \right) R_m \left( \beta_{2} \right)
\dots R_n \left( \alpha_{N/2} \right) R_m \left( \beta_{N/2} \right)\right) \lt N \varepsilon_{N} $
となり、この計算誤差の範囲で等しくなり、ユニタリ演算 $U$ が Tゲートと Hゲートだけで表すことができました。
Solovay-Kitaev の定理
本稿の本題です。目的である「任意の1量子ビット演算の近似的な分解」は上記で示せましたが、この分解の効率については考ませんでした。ここで、ある量子計算の問題 $A$ に対して、ある量子アルゴリズムがあり、その計算には $N_A$ 個の量子ゲートで正確に表せるとします。この同じ問題の解法を、同じ計算精度 $ \varepsilon $ の範囲で Tゲートと Hゲートだけで表す式が複数あれば、よりゲート数が少ない方が、ノイズの混入も少なく、計算時間も短くできて効率的です。
そういった要求を叶えるのが『Solovay-Kitaev の定理』です。『Solovay-Kitaev の定理』を使うと、同じ問題の解法を、同じ計算精度 $ \varepsilon $ の範囲で、より短く Tゲートと Hゲートだけで表すことができます。この定理は、著名な教科書『Quantum Computation and Quantum Information: 10th Anniversary Edition』(Cambridge University Press)の付録(Appendix 3)に詳しい解説があります。正確な証明は教科書を読んでいただきたいですが、ここではその証明の概要を取り上げます。
(Solovay-Kitaev の定理) $\mathscr{G}$ は $SU \left( 2 \right)$[*1](#su2)の要素とその逆元を含む要素をもつ有限集合[*2](#set-g)であり、$\langle \mathscr{G} \rangle$ [*3](#set-gt)が $SU\left(2\right)$で稠密[*4](#dense)であるとします。 $\varepsilon \gt 0$ が与えられたとき、 $l = O\left(\log^{c}{ \left( 1 / \varepsilon \right) } \right)$である $\mathscr{G} _{l}$ [*5](#set-gl)が、$SU \left( 2 \right)$ に対して $\varepsilon $ネット[*6](#e-net) となるある定数 $c$ が存在します。
定理の内容を理解するだけでも難儀しそうです。以下に、定理に使われている用語の定義を簡潔に補足します。
*1: $SU \left( 2 \right)$の数学的な定義はほかにありますが「行列式が1に等しいすべての1量子ビットのユニタリ行列の集合」です。
*2: 集合の記号で書くと、$\mathscr{G} = { u_k \ \vert\ u_0, u_1 ,..., u_n, u_0^{-1}, u_1^{-1} , \dots , u_n^{-1} \in SU \left( 2 \right) }$です。例としては、$\mathscr{G} = {H, S, T, S^{\dagger} \left( = S^3 \right), T^{\dagger} \left( = T^7 \right)\}$ が具体的な集合です。
*3: $\langle \mathscr{G}\rangle$ は $\mathscr{G}_{l}$ の任意の長さ $l$ の語をもつ集合すべての有限集合とします。
*4: $SU \left( 2 \right)$ の部分集合 $\langle \mathscr{G} \rangle$ が稠密であるとは、$SU \left( 2 \right)$ の任意の要素 $U$ と $\varepsilon \gt 0$ に対して、トレース距離 $D\left(\Gamma,U\right) \lt \varepsilon$ となる要素 $\Gamma \in \langle \mathscr{G} \rangle$ が存在するということです。つまり、どんなユニタリ $U$ をとっても、近似できる $ \Gamma $ が存在するということを言っています。
*5: $\mathscr{G}$ の要素から作られる高々 $l$ 個の積を、中さ $l$ の語(word)といい、そのすべての語の集合を $ \mathscr{G} _{l} $ と記します。例としては、$\mathscr{G} _{2} = { HS, SH, HT, TH, HS^{\dagger}, S^{\dagger}H, HT^{\dagger}, T^{\dagger}H, \dots}$ です。
*6: $SU \left( 2 \right)$ のあらゆる要素 $U$ が、$\mathscr{G}$ のある要素 $\Gamma$ からの距離が $ \varepsilon $ 以内であるときに、「G は $SU \left( 2 \right)$ に対して、$ \varepsilon $ネットである」といいます。
Solovay-Kitaev の証明は、$c \approx 4$ として示せます。また、$c$ を 2 近辺まで減らせる方法が分かっており、さらに、1 以下にはならないことが示されています。しかし、最良な下界値を求める問題は、未解決問題のようです。
ここまでで用語の定義は、一通り分かった(?)わけですが、これを証明するのは専門家ではない私のような者にはかなり厳しそうです。頑張って、その雰囲気だけでも感じてみたいと思います。
それには、次の補題を使います。
これまた難易度高めですが、補題の内容にある用語はすべてSolovay-Kitaevの定理の中にあるものと同じです。この補題の意味するところを感じてみますと、
ゲート数を表す語(word)の長さを $l$ から $5l$ の5倍をとると、必ず $\varepsilon^{2}$ネット から $\varepsilon^{3}$ネットという 2乗から3乗にできるような、精度 $\varepsilon$の上界 $\varepsilon _{0}$が存在するということです。ゲート数を高々5倍にするだけで、その誤差範囲は2乗から3乗に急速に狭められることを示しているようです。
これはかなり効率が良さそうな話しです。ここでは、この補題は証明なしで受け入れましょう。すると、次のアウトラインで『Solovay-Kitaev の定理』が証明ができるようです。
Solovay-Kitaev の証明のアウトライン
- (補題)を繰り返し使って、語の長さ $l$ が増加すると、原点近傍が急速に充足されます。
- $\displaystyle \varepsilon \left( k \right) = \frac{\left( C \varepsilon _{0} \right) ^{\left( 3/2 \right) ^{k}}}{C} \dots (★)$
とおいて、次のように、並進ステップのテクニックを使います。
任意のユニタリ $ U \in SU \left( 2 \right)$ を、
まず、$\mathscr{G}$ から $ l _{0} $ 個のゲートを使って $\varepsilon \left( 0 \right) ^{2}$ 以内で近似する
次に、 $\mathscr{G}$ から $5 l _{0} $ 個のゲートを使って $\varepsilon \left( 1 \right) ^{2}$ 以内で近似する
:
そして、$\mathscr{G}$ から $ 5^k l _{0} $ 個のゲートを使って $\varepsilon \left( k \right) ^{2}$ 以内で近似する
- $ l _{0} + 5 l _{0} + \cdots + 5^k l _{0} \lt \frac{5}{4} \cdot 5 ^{k} l _{0}$ 個のゲートを用いて、$\varepsilon \left( k \right) ^{2} \lt \varepsilon $ の精度で任意のユニタリ演算子 $U$ を近似できます。
式(★)を使うと、精度$\varepsilon$について次式が示せます。
$\begin{equation}
\left.\begin{aligned}
\left( \frac{3}{2} \right)^{k} < \frac{\log \left( 1 / C^2 \varepsilon \right) }{ 2 \log \left( 1 / C \varepsilon _{0} \right) }
\end{aligned} \right.
\end{equation}$
ここで、$\begin{equation}
\left.\begin{aligned}
c = \log 5 / \log \left( 3 / 2 \right) \approx 4
\end{aligned} \right.
\end{equation}$ を用いると、ゲート数 $l$ が Solovay-Kitaev にある $O\left(\log^{c}{ \left( 1 / \varepsilon \right) } \right)$ であることが次の関係式として示せます。
$\displaystyle \text{number of gates} \lt \frac{5}{4} \cdot 5^{k} l _{0} = \frac{5}{4} \left( \frac{3}{2} \right) ^{kc} l _{0} \lt \frac{5}{4} \left( \frac{\log \left( 1 / C^2 \varepsilon \right) }{ 2 \log \left( 1 / C \varepsilon _{0} \right) } \right)
^{c} l _{0} $
この式の最後の項が、$O\left(\log^{c}{ \left( 1 / \varepsilon \right) } \right)$ を表しています。
まとめ
「量子状態は壊れやすい」「正確に量子操作するのも困難である」ために、誤り制御をしつつ、量子計算を継続できる機構が「量子誤り訂正」です。これにはある一定の精度を定めて、その精度以下で量子誤り訂正を動作させることができます。そのために、CNOTゲート(CX), Hadamardゲート(H), 位相ゲート(S), π/8ゲート(T) の量子演算のセットで任意の量子演算を表す必要がでてきます。
それを効率的に可能にする理論が、『Solovay-Kitaev の定理』です。この理論の証明を、雰囲気レベルで取り上げました。
この Solovay-Kitaev の実装は、様々公開されているものがあります。ここでは1つ紹介するに留めます。gridsynthは、任意のZ軸回転操作を Tゲートと Hゲートだけで表すツールです。ソースコードからの実行するには、Haskell のビルド・実行環境を整える必要がありますが、バイナリビルドもありますので、試してみてはいかがでしょうか。
教科書を読まれるとわかりますが、本稿は教科書の写経に近い内容となっております。教科書を読まずに雰囲気だけでも知りたい方には、要約的に抜粋していますので流れがお伝えできていれば幸いです。それでも、抜粋であるのと解説文が的を得ていないことにより、かえって分かりづらくなっているとすれば、大変申し訳ないです。もしお気づきの点などあれば修正していきますので、コメント頂けると嬉しいです。
Appendix
A1. 数学的な準備:軸周りの任意角回転のユニタリ演算子
軸 $\vec{n}=(n_x, n_y, n_z)$まわりの角$\theta$の回転を表すユニタリ演算$R_{\vec{n}} \left( \theta \right) $は次式で定義されます。(四元数のスピナー表現で三次元ロドリゲスの回転公式に対応しています。)
$\begin{equation}\left.\begin{aligned}
R_{\vec{n}} \left( \theta \right) \equiv
\exp {\left( -i \frac{\theta}{2} \vec{n} \cdot \vec{\sigma} \right)}
= \cos{\frac{\theta}{2}} I - i \sin{\frac{\theta}{2}} \left( n_x \sigma_x + n_y \sigma_y + n_z \sigma_z \right)
\end{aligned} \right.\end{equation}$
Pauli行列の指数関数は、それぞれ $x ,y, z$ 軸まわりの回転 $R_x \left( \theta \right), R_y \left( \theta \right),R_z \left( \theta \right) $ として、次式で定義されます。
$\begin{equation}\left.\begin{aligned}
R_x \equiv \exp {\left( -i \frac{\theta}{2} \sigma_x \right)}
= \cos{\frac{\theta}{2}} I - i \sin{\frac{\theta}{2}} \sigma_x
= \left( \begin{matrix}
\cos{\frac{\theta}{2}} & -i \sin{\frac{\theta}{2}} \\ -i \sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}}
\end{matrix} \right)
\end{aligned} \right.\end{equation}$
$\begin{equation}\left.\begin{aligned}
R_y \equiv \exp {\left( -i \frac{\theta}{2} \sigma_y \right)}
= \cos{\frac{\theta}{2}} I - i \sin{\frac{\theta}{2}} \sigma_y
= \left( \begin{matrix}
\cos{\frac{\theta}{2}} & - \sin{\frac{\theta}{2}} \\ \sin{\frac{\theta}{2}} & \cos{\frac{\theta}{2}}
\end{matrix} \right)
\end{aligned} \right.\end{equation}$
$\begin{equation}\left.\begin{aligned}
R_z \equiv \exp {\left( -i \frac{\theta}{2} \sigma_z \right)}
= \cos{\frac{\theta}{2}} I - i \sin{\frac{\theta}{2}} \sigma_z
= \left( \begin{matrix}
e^{- i \frac{\theta}{2}} & 0 \\ 0 & e^{i \frac{\theta}{2}}
\end{matrix} \right)
\end{aligned} \right.\end{equation}$
A2. 数学的な準備:演算子に対する近似の定義
(定義)ユニタリ演算子の近似
目的のユニタリ演算: $U$ に対し、その演算に対しての近似的な演算: $V$ として、誤差を次のように定義します。
$\begin{equation}\left.\begin{aligned}
E\left(U, V \right) \equiv \underset{\lvert \psi \rangle}{\max} || (U - V) \lvert \psi \rangle ||
\end{aligned} \right. \end{equation}$
複数の演算の積を、すべて近似的な演算の積とする場合には、その誤差は次のようになります。
$\begin{equation}\left.\begin{aligned}
E\left(U_m U_{m-1} \dots U_1, V_m V_{m-1} \dots V_1 \right) \le \sum_{j=1}^{m} E\left(U_j, V_j \right)
\end{aligned} \right. \end{equation}$
また、トレース距離を次の式で定義します。
$\begin{equation}\left.\begin{aligned}
D\left(U, V \right) \equiv tr | U - V |
\end{aligned} \right. \end{equation}$
-
@kyamaz
 が運営する OpenQLプロジェクトは、量子コンピューターを扱うための様々なライブラリを開発するためのオープンソースプロジェクトです。量子情報、量子コンピューターに興味がある人たちが集うコミュニティを運営しております。詳しくはconnpassのサイトをご覧ください。 ↩
が運営する OpenQLプロジェクトは、量子コンピューターを扱うための様々なライブラリを開発するためのオープンソースプロジェクトです。量子情報、量子コンピューターに興味がある人たちが集うコミュニティを運営しております。詳しくはconnpassのサイトをご覧ください。 ↩ -
数学的な準備:演算子に対する近似の定義 を参照。 ↩