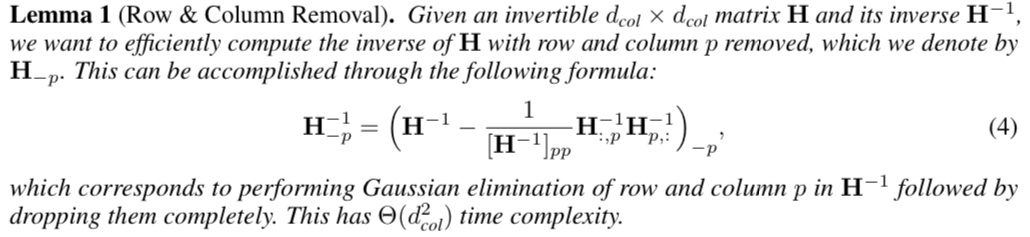紹介する論文1
タイトル:Optimal Brain Compression: A Framework for Accurate Post-Training Quantization and Pruning
学会:NeurIPS 2022
Optimal Brain SurgeonのPost-training枝刈りを高速に行う方法を提案しています。
また、Optimal Brain Surgeonに着想を得た量子化方法のOptimal Brain Quantization (OBQ) を提案しています。
Optimal Brain Surgeon
Optimal Brain Surgeonは、1992年にLeCunらが発表した枝刈り方法です。いくつかの重みを0にすることで過学習を抑制する方法として提案されました。2
Optimal Brain Surgeonでは、枝刈りしつつ2乗誤差のズレを小さくしたいという考え方で枝刈りします。
ニューラルネットワークの重みを$\mathbf{w}$とし、ロス関数$E(\mathbf{w)}$を、ある1個のサンプル$\mathbf{x}$に対する2乗誤差とします。ここで、枝刈りで重みを$\mathbf{w}$から$\mathbf{w}+\mathbf{\delta w}$に変えた時のロスの変化量$\delta E$を考えます。$E(\mathbf{w)}$の$\mathbf{w}$の周りのテイラー展開を考えると、
\delta E = \left(\frac{\partial E}{\partial \mathbf{w}} \right)^T \delta\mathbf{w} + \frac{1}{2} \delta\mathbf{w}^T\mathbf{H}\delta\mathbf{w} + O(||\delta\mathbf{w}||^3)
ここで、$\mathbf{H}$は$E$のヘッセ行列です。
十分学習されており、重み$\mathbf{w}$が最適値に近い状況では$\frac{\partial E}{\partial \mathbf{w}}\approx\mathbf{0}$です。また、$\delta\mathbf{w}$の3乗の項を無視すると、
\delta E \approx \frac{1}{2} \delta\mathbf{w}^T\mathbf{H}\delta\mathbf{w}
です。この目的関数を最小化したいと考えます。
今、重み$\mathbf{w}$のうち$q$番目のパラメータ$w_q$を0にした(枝刈りした)とすると、制約条件は$\delta w_q+w_q=0$つまり$\mathbf{e}_q^T\delta\mathbf{w}+w_q = 0$が課されることになります。ここで、$\mathbf{e}_q$は第$q$成分のみが1の単位ベクトルです。
目的関数と制約条件をまとめると、ラグランジュの未定乗数法より
L=\frac{1}{2} \delta\mathbf{w}^T\mathbf{H}\delta\mathbf{w} + \lambda(\mathbf{e}_q^T\delta\mathbf{w}+w_q)
がラグランジアンになります。$\lambda$は未定乗数です。
これの解は以下のようになります。
\delta\mathbf{w} = -\frac{w_q}{[\mathbf{H}^{-1}]_{qq}}\mathbf{H}^{-1}\mathbf{e}_q
L_q = \frac{1}{2}\frac{w_q^2}{[\mathbf{H}^{-1}]_{qq}}
ここで、$[\mathbf{H}^{-1}]_{qq}$は$\mathbf{H}^{-1}$の第$(q, q)$成分を表します。
Optimal Brain Surgeonのアルゴリズムは以下のようになります。
- ニューラルネットワークを学習する。
- $\mathbf{H}^{-1}$を計算する。
- $L_q$を最小化する$q$を探す。$q$が何らかの枝刈りの終了条件を満足するなら終了する。そうでないなら$q$番目の重みを刈る($w_q$を0にする)
- $\delta\mathbf{w}$を計算する。$q$番目以外の重みを、$\delta\mathbf{w}$によって更新する。
- 2に戻る。
ステップ3の枝刈りで生じたズレを、他の部分の重みで補正する(ステップ4) ことがポイントです。
また$\mathbf{H}^{-1}$を計算する時に$\mathbf{x}$が含まれますが、$\mathbf{x}$に全てのサンプルを入れた時の合計を考えれば良いということになります。
Optimal Brain Compression
Optimal Brain Compressionでは、レイヤ毎にOptimal Brain Surgeonを適用して2乗誤差を最小化することを考えます。
以下では、あるレイヤのニューラルネットワークの重みを$\mathbf{W}\in\mathbf{R}^{d_{row}\times
d_{col}}$とし、入力を$\mathbf{X}\in\mathbf{R}^{d_{col}\times c}$と書くことにします。
$d_{row}$は出力のチャネル数、$c$は入力のチャネル数のイメージです。畳み込み演算の場合は、フィルタ1チャネル分のパラメータが$\mathbf{W}$の1列に並べられていることになります。
パラメータ数を$d=d_{row}d_{col}$と置くと、Hessianの逆行列計算に$O(d^3)$かかり、これを$d$回繰り返すので、全計算量は$O(d^4)$と多いです。
Optimal Bran Compressionは、Optimal Brain Surgeonの計算量を削減するExactOBSと、Optimal Brain Surgeonを量子化に応用するOptimal Brain Quantizationからなります。
ExactOBS
Optimal Brain Surgeonの2乗誤差は$||\mathbf{W}\mathbf{X}-\mathbf{\hat{W}}\mathbf{X}||_2^2$です。
2乗誤差は出力チャネルに独立なので、$\sum_{i=1}^{d_{row}}||\mathbf{W_{i,:}}\mathbf{X}-\mathbf{\hat{W}_{i,:}}\mathbf{X}||_2^2$と書くことができます。
つまり、行を1つ固定した時の$||\mathbf{W_{i,:}}\mathbf{X}-\mathbf{\hat{W}_{i,:}}\mathbf{X}||_2^2$を最小化する問題を考えれば良いことになります。
ExactOBSでは、行を1つ固定してOptimal Brain Surgeon (OBS)を適用します。アルゴリズムは論文のAlgorithm 1です。
ExcactOBSがOptimal Brain Surgeonと異なるのは、(1)ヘッセ行列の逆行列計算を高速化していることと、(2)枝刈り回数を$k$回に制限することで計算量を減らしていることです。
(1)はAlgorithm 1の5行目に対応し、Lemma 1から従います。
Lemma 1は、ヘッセ行列の逆行列の計算の高速化の肝となる公式です。"ある行列$\mathbf{H}$から第$p$行・第$p$列を除いた行列の逆行列$\mathbf{H}_{-p}^{-1}$は、除く前の逆行列$\mathbf{H}^{-1}$と、その第$p$行・第$p$列で表せる"というものです。
Optimal Brain Quantizer (OBQ)
Optimal Brain Quantizer (OBQ) は、Optimal Brain Surgeonの考え方を量子化に適用したものです。
Optimal Brain Surgeonの最適化の式は、枝刈りで重みを$\mathbf{w}$から$\mathbf{w}+\mathbf{\delta w}$に変えた時のロスの変化量$\delta E$を考え、下記のラグランジアンに帰着させました。制約条件は$\mathbf{e}_p^T\delta\mathbf{w}+w_p=0$です。
L=\frac{1}{2} \delta\mathbf{w}^T\mathbf{H}\delta\mathbf{w} + \lambda(\mathbf{e}_p^T\delta\mathbf{w}+w_p)
Optimal Brain Quantizerでは、量子化で重みを$\mathbf{w}$から$\mathbf{w}+\mathbf{\delta w}$に変えた時のロスの変化量$\delta E$を考えます。
量子化を$\mathrm{quant}(\cdot)$で書くことにすると、$\mathrm{quant}(w_p)=w_p+\mathbf{e}_p^T\mathbf{\delta w}$つまり$\mathbf{e}_p^T\mathbf{\delta w}+w_p-\mathrm{quant}(w_p)=0$が制約条件になります。
2つの制約条件を見比べると、Optimal Brain Quantizerでは、Optimal Brain Surgeonの$w_p$を、$w_p-\mathrm{quant}(w_p)$に置き換えた式が成り立つことになります。
L_p = \frac{1}{2}\frac{(w_p-\mathrm{quant}(w_p))^2}{[\mathbf{H}^{-1}]_{pp}} \rightarrow \mathrm{min}
p = \mathrm{argmin}_p L_p
\delta\mathbf{w} = -\frac{w_p-\mathrm{quant}(w_p)}{[\mathbf{H}^{-1}]_{pp}}\mathbf{H}^{-1}\mathbf{e}_p
Optimal Brain Quantizaterのアルゴリズムは以下のようになります。
- ニューラルネットワークを学習する。
- ヘッセ行列の逆行列$\mathbf{H}^{-1}$を計算する。
- $L_p$を最小化する$p$を探す。$p$番目の重みを量子化する。
- $\delta\mathbf{w}$を計算する。$p$番目以外の重みを、$\delta\mathbf{w}$によって更新する。
- もし何らかの終了条件を満たしていれば終了する。
- 2に戻る。
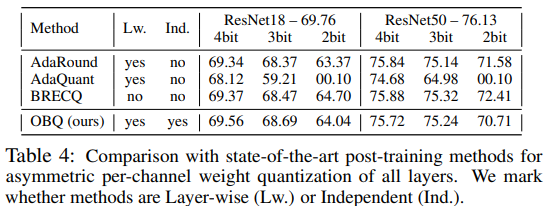
評価
Optimal Brain Quantizer (OBQ) の量子化性能の評価を見てみます。OBQはレイヤ間で独立に処理しても、従来のレイヤ間でシーケンシャルに処理する方法と同じくらいの精度と主張しています。