紹介する論文1
タイトル: GPTQ: Accurate Post-Training Quantization for Generative Pre-trained Transformers
学会: ICLR2023
GPTQは大規模言語モデル向けの量子化方法です。
Llama2-13bのような、パラメータ数が数十Billionクラスのモデルの4bit量子化や3bit量子化に使われているPost-trainingの量子化方法です。
数百Billion級のモデルを3、4bit量子化する方法は初と主張しています。
LLMにOptimal Brain Quantiationを適用する
GPTQの基本的なアイデアは、LLMにOptimal Brain Quantization (OBQ)による量子化を適用するというものです。
しかし、パラメータ数が数Billionクラスになると、単にOBQを適用するだけでは精度が落ちると指摘しています。OBQの終盤で大きな誤差を補正する必要があるため、補正が困難になります。反復計算で得られるヘッセ行列の逆行列が正定値でなくなり、数値的に不安定になるそうです。
本論文では、LLMにOBQを適用する際の数値不安定性を解決しつつ、高速化する方法を提案しています。
パラメータの更新順序
OBSやOBQでは、量子化誤差が最小になるパラメータから貪欲に更新パラメータを選択していました。しかしこの順序であることは必ずしも必須ではないです。GPTQではパラメータを添え字の小さい方から順に量子化しています。
バッチ化
Lazy Batch-Update (遅延バッチ化) ではメモリボトルネックを解消することで高速化します。ヘッセ行列の逆行列や重み行列の補正を1列ずつ行うのではなく、$B=128$個まとめて行うことによってメモリ効率を上げます。
Cholesky Reformulation
一般に、正定値行列$A$は、下三角行列$L$を用いて$A=LL^T$と分解することができます。これをコレスキー(Cholesky)分解と呼びます。
GPTQの話に戻ります、GPTQでは、精度劣化の問題に対して、Cholesky Reformulationで数値不安定性を解決することを提案しています。
OBSのヘッセ行列の逆行列の更新式は、よく見るとコレスキー分解の更新式と似ています。これを用いると、コレスキー分解のソルバーを使ってヘッセ行列の逆行列を更新できます。LAPACKのコレスキー分解ルーチンなどを使って計算すれば、数値安定に計算できるという訳です。
評価
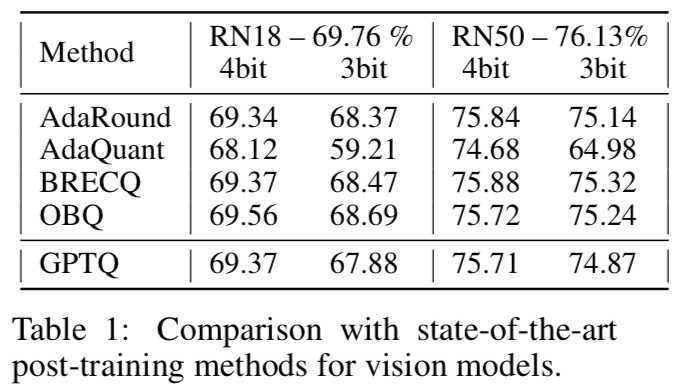
Table 1 はResNetによる画像認識タスクで評価しています。GPTQがAdaRoundやAdaQuantといった量子化方法と同程度であることが確認できます。
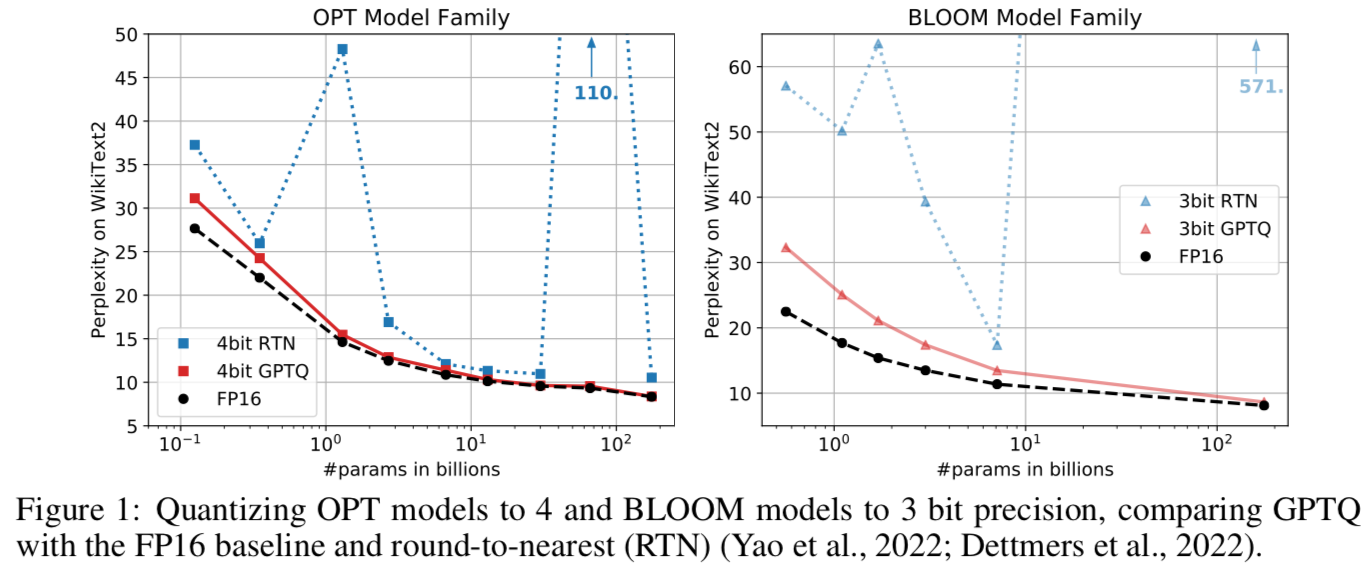
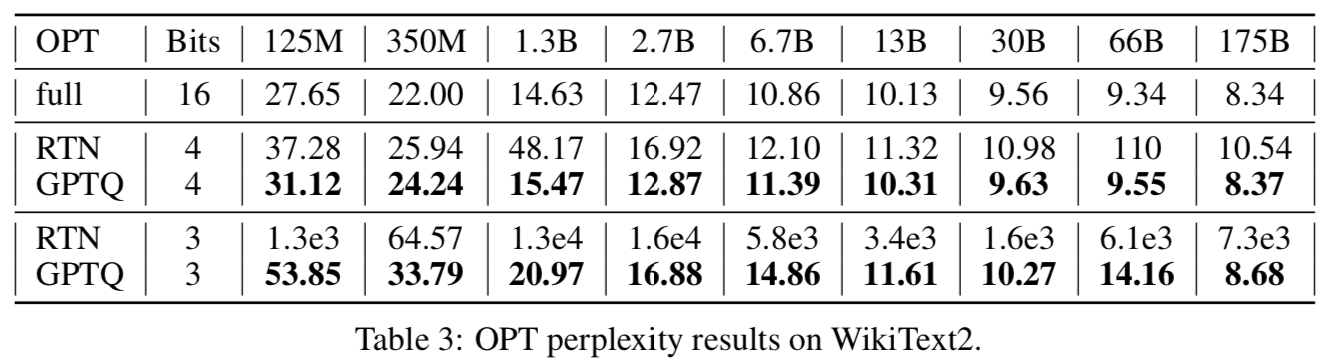
Table 3ではLLMによる言語処理タスクで比較しています。GPTQは3bitや4bitでも数十〜数百Billionパラメータのモデルを量子化しても精度劣化が小さいことが確認できます。
-
画像や数式は論文から引用しています。 ↩