【ノンパラメトリックベイズ】ディリクレ過程を用いたクラスタ数推定

概要

こんにちは、kwashiです。機械学習のはやりとともに、教師なし学習の分野も盛り上がってきています。教師なし学習といえばトピックモデルが有名です。トピックモデルは潜在的意味を推定するための手法です。この目的の１つとして、潜在的意味、例えば、ニュース記事のカテゴリなどを取得することがあります。このトピックモデルでは、ディリクレ過程を用いて各文書のトピック分布(カテゴリの数)を取得しています。

また、音源分離の論文を紹介しますが、Bayesian Nonparametrics for Microphone Array Processingは、複数音源による複数マイク(マイクロホンアレイ)への入力から、音源方向+分離音を推定する手法を説明しています。この論文の主題にもある通り、ノンパラメトリックベイズを用いることで、ディリクレ過程で音源数を求めています。音源数というものはとても、重要です。なぜなら、何個の分離音を生成すべきなのか手がかりになるからです。

本記事では、このノンパラメトリックベイズとしてディリクレ過程を用いたクラスタ数と正規分布の平均、分散を同時に推定する例を用いて説明していきます。

目的

本記事では、以下のような混合正規分布から生成した学習データより、各正規分布の平均,分散を求めます。まず、最初にクラスタ数を指定した状態で各正規分布を推定方法を説明し、その後、クラスタ数も同時に推定する方法について説明します。

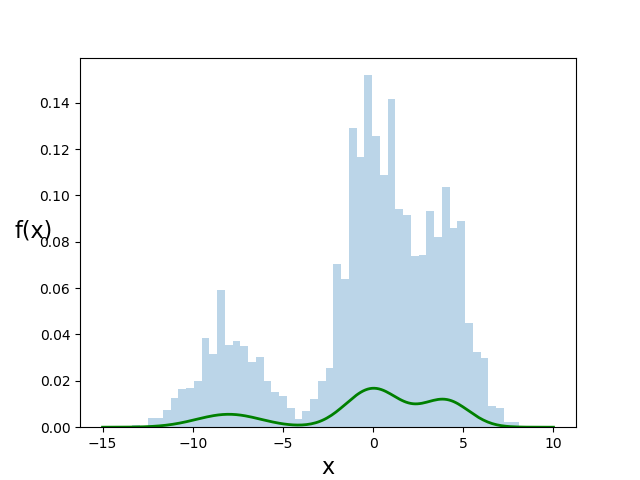
各正規分布の値は、平均(-8, 0, 4), 分散(1.8, 1.5, 1.3),正規分布の混合率(0.2, 0.5, 0.3)です。下図に、生成した確率密度分布(緑線)と生成したデータの頻度を示しています。また、混合正規分布とデータ生成のプログラムを記載しています。

※ベイズ推論のライブラリとしてpymc3を用いています。

import pymc3 as pm
import numpy as np
import theano.tensor as tt
import scipy.stats as stats
from scipy import optimize
import matplotlib.pyplot as plt

np.random.seed(53536)

xmin = -15.
xmax = 10.
xsize = 200
x = np.linspace(xmin, xmax, xsize)
pi_k = np.array([0.2, 0.5, 0.3])
loc_x = np.array([-8, 0, 4])

norm1 = stats.norm.pdf(x, loc=loc_x[0], scale=1.8) * pi_k[0]
norm2 = stats.norm.pdf(x, loc=loc_x[1], scale=1.5) * pi_k[1]
norm3 = stats.norm.pdf(x, loc=loc_x[2], scale=1.3) * pi_k[2]

npdf = norm1 + norm2 + norm3
npdf /= npdf.sum()

#確率分布の確率に則って値(x)を取得
y = np.random.choice(x, size=4000, p=npdf)

クラスタ数固定 正規分布推定

本章では、クラスタ数を3と予め決めた状態で、３つの正規分布の平均と分散を推定する方法を説明します。クラスタ数を決めた状態で、正規分布のパラメータを推定する手法は、多々あり、例えば、EMアルゴリズムや変分ベイズ, マルコフ連鎖モンテカルロ法(Markov chain Monte Carlo methods; MCMC)などがあります。本章では、MCMCを用います。

正規分布の生成モデルは、以下のプログラムの通りです。ディリクレ分布から生成される各正規分布の混合率をパラメータとしてカテゴリカル分布が各データがどのグループに属するかを表すID(z)を生成します。あとは、各正規分布に対して、平均と分散に値する分布を設定しています。

with pm.Model() as model:
  p = pm.Dirichlet('p', a=np.ones(cluster))
  z = pm.Categorical('z', p=p, shape=y.shape[0])

  mu = pm.Normal('mu', mu=y.mean(), sd=10, shape=cluster)
  sd = pm.HalfNormal('sd', sd=10, shape=cluster)

  y = pm.Normal('y', mu=mu[z], sd=sd[z], observed=y)

  trace = pm.sample(1000)

しかし、このモデルでは、隠れ変数zがあるため計算が遅いです。そのため、周辺化(∫p(y|z,θ)dz -> p(y|θ))を行い、以下のようにプログラムを修正します。
※混合分布の成分を入れ替えることができる場合、混合成分の入れ替わり、label switching problem が発生してしまうため、その対処としてMCMCを実行するpm.sampleにてchains=1と設定しています。

with pm.Model() as model:
  p = pm.Dirichlet('p', a=np.ones(cluster))
  mu = pm.Normal('mu', mu=y.mean(), sd=10, shape=cluster)
  sd = pm.HalfNormal('sd', sd=10, shape=cluster)

  y = pm.NormalMixture('y', w=p, mu=mu, sd=sd, observed=y)

  trace = pm.sample(3000, chains=1)

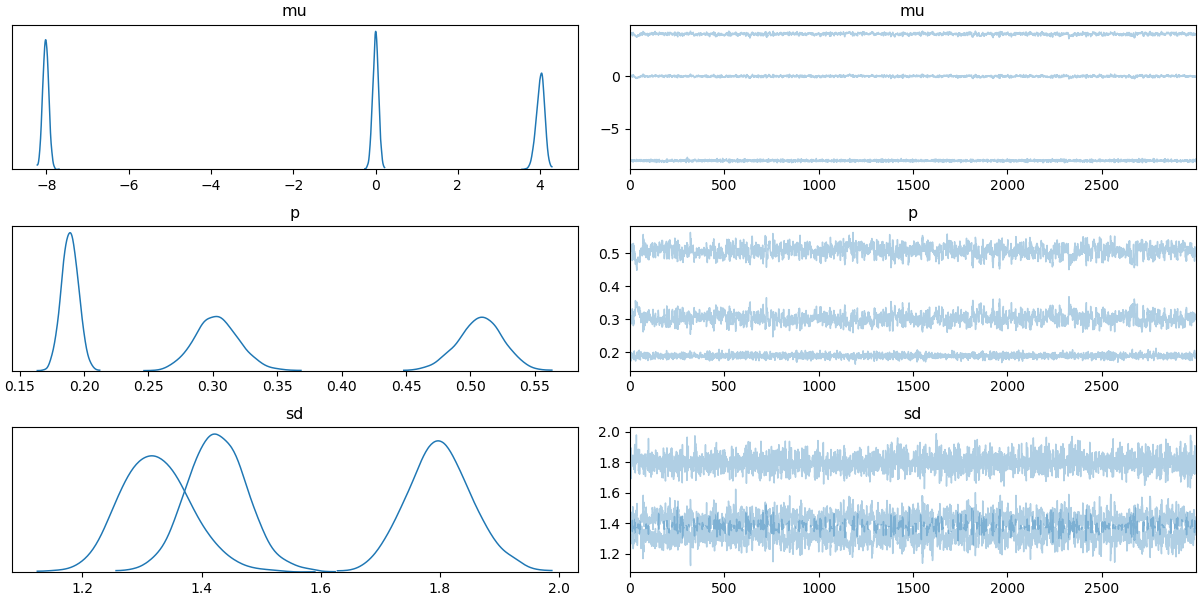
推論の結果を下図に示します。各正規分布の平均(-8, 0, 4)(mu), 分散(1.8, 1.5, 1.3)(sd),正規分布の混合率(0.2, 0.5, 0.3)(p)が上手く推定されることが見て取れます。

クラスタ数未知　正規分布推定

前章では、クラスタ数が既知である前提で、正規分布のパラメータを推定しました。本章では、ディリクレ過程を導入することで、クラスタ数未知の場合の正規分布パラメータ推定を説明します。本章では、ディリクレ過程のイメージを解説することを優先します。ディリクレ過程の詳細は、続・わかりやすいパターン認識―教師なし学習入門がとても参考になるので、ぜひ読んでみてください。

ディリクレ過程(DP)を簡単に説明すると、H~ DP(a, H'), aが集中度(分散のようなイメージ)とH(基底分布; 平均のようなイメージ)で表され、DPにより分布Hが生成されます。このことから、分布に対する分布と呼ばれることもあります。私の個人的なイメージでは、ガウス過程を用いた回帰でガウス過程により回帰関数自体を推論していると述べているように、ディリクレ過程も分布自体を推論しているというイメージです。

さて、このディリクレ過程を実現する手法として、中華料理過程(CRP)や棒折り過程(stick breaking process; SBP)があります。本章では、このSBPを用いる手法を説明していきます。SBPは、以下の式で表されます。Kが分布数。Kが無限のとき、無限次元のディリクレ分布をSBPで示すことができます。(実際に使用するときは、Kを有限の定数に設定します。)

{\pi_k = b_k \prod_{j=1}^{K-1} (1-b_j),\,b_k \sim {\rm Beta}(b;1,\alpha) } 

この式の結果πは、クラスタkの混合比です。このSBPのプログラムと結果を以下に示します。しかし、このSPBだけでは、分布の平均などを求めることはできません。そのため、以下の式のように基底分布から値を生成し、横軸としています。

{  \theta _ { k } \sim H _ { 0 } , \text { for } k = 1 , \ldots , K } 

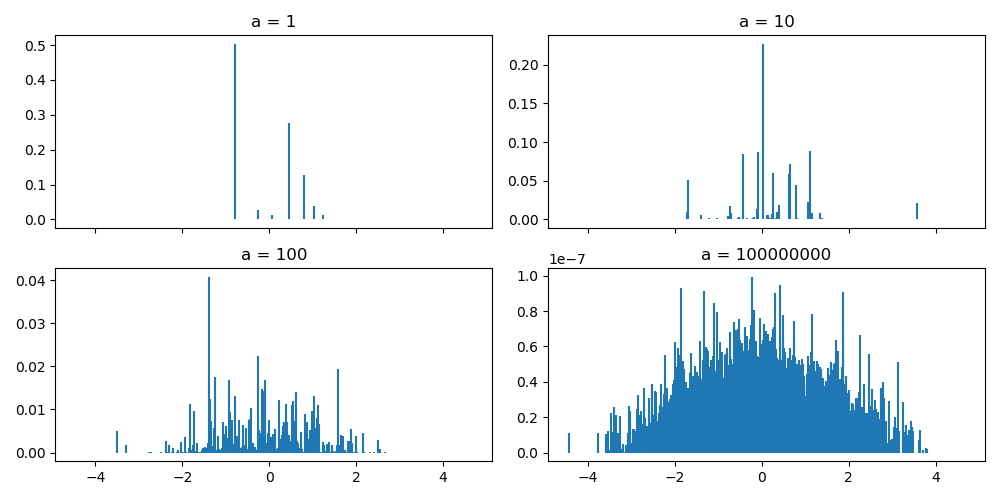
下図は、各位置にどの混合比が生成されたかを示しています。aが小さいなら中心に集中していますが、aが大きいほど、外にばらけているのがわかります。

def stick_breaking(a, h, k):
  '''
  a:集中度
  h:基底分布(scipy dist)
  K: コンポーネント数

  Return
  locs : 位置(array)
  w: 確率(array)
  '''
  s = stats.beta.rvs(1, a, size=K)
 #ex : [0.02760315 0.1358357  0.02517414 0.11310199 0.21462781]
  w = np.empty(K)
  w = s * np.concatenate(([1.], np.cumprod(1 - s[:-1])))
  #ex: 0.02760315 0.13208621 0.0211541  0.09264824 0.15592888]
  # if i == 1, s , elif i > 1, s∑(1-sj) (j 1 -> i-1)

  locs = H.rvs(size=K)
  return locs, w

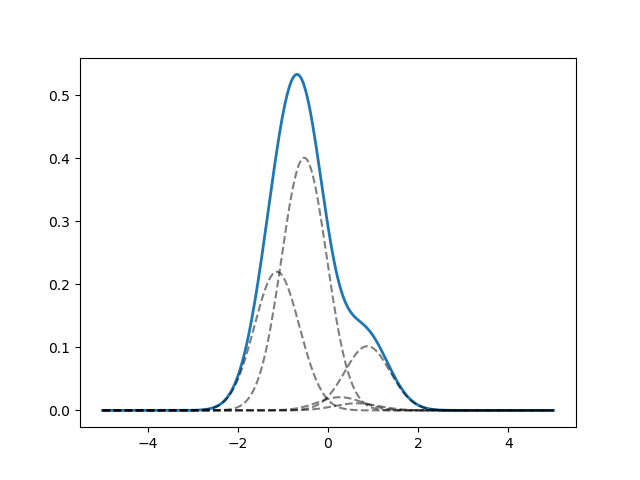
次に、K=5の場合のSPBにより生成した混合比と基底分布(正規分布)から生成した平均により表現された正規分布を示します。分散は一定としています。この図のように、SPBのパラメータaと基底分布を変更することで、あらゆる混合正規分布が表現できることがわかります。

さて、このようにSPBにより混合比を生成していることを踏まえて、クラスタ数未知の場合の正規分布パラメータ推定を行います。pymcの形式に合わせて以下のようなプログラムを書きました。SPBからは、混合比のみ出力しています。また、SPBのハイパーパラメータaは、ガンマ分布より生成しています。そして、平均,分散を正規分布から生成しています。Kは有限個(20)に設定しています。

def stick_breaking_DP(a, K):
  b = pm.Beta('B', 1., a, shape=K)
  w = b * pm.math.concatenate([[1.], tt.extra_ops.cumprod(1. - b)[:-1]])
  return w

K = 20

with pm.Model() as model:
  a = pm.Gamma('a', 1., 1.)
  w = pm.Deterministic('w', stick_breaking_DP(a, K))
  mu = pm.Normal('mu', mu=y.mean(), sd=10, shape=K)
  sd = pm.HalfNormal('sd', sd=10, shape=K)

  y = pm.NormalMixture('y', w=w, mu=mu, sd=sd, observed=y)

  trace = pm.sample(1000, chains=1)

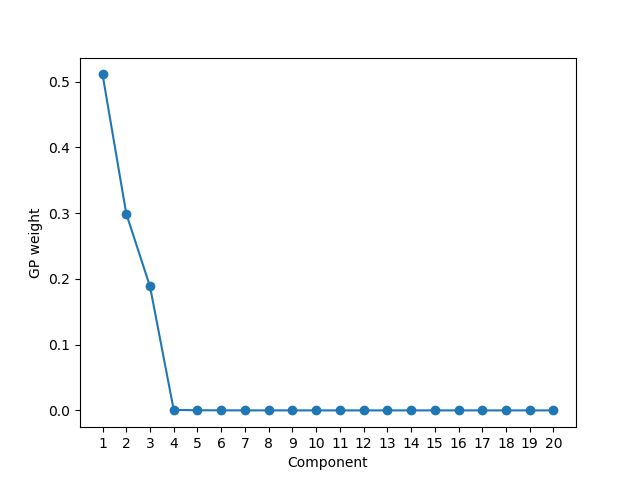
推定した混合数を以下に示します。このように、大きな値を持っている混合比が3であることからクラスタ数が3つあることが推定できています。(実際の値は、0.2, 0.5, 0.3)また、他の平均、分散は、クラスタありの場合とほとんど同じでした。ここで重要なことは、クラスタもともに推定できているということです。

まとめ

本記事では、ノンパラメトリックベイズとして、ディリクレ過程を用いたクラスタ数の推定を、正規分布の推定と同時に行う手法を説明した。説明をイメージ優先で行ったので、違和感を抱く人もいるかも知れませんが、その際は、せひご指導のほどよろしくお願いいたします。