はじめに
機械学習を学ぶのに最適な教材と言われるcouseraのMachine Learningを現在受講しているので学んだことを整理する目的でまとめていこうと思います。
1週目の内容は機械学習・教師あり学習・教師なし学習についてです。
couseraのMachine Learning講座について
1週目なのでこの講義について簡単に説明しておきます。
couseraとは有名大学の講師が行なっている講義をオンラインで学習できる動画教材です。
machine learning講座ではcouseraの共同創業者でスタンフォード大学で機械学習の教鞭を執っているAndrew Ng先生が開講しています。
機械学習(Machine Learning)の定義
アーサー・サミュエルが提唱した定義:
機械学習はコンピュータに明示的にプログラムすることなく学習する能力を与える研究分野。
これは非形式的な定義で、やや古いそうです。
トム・ ミッチェルが提唱した定義:
コンピュータ・プログラムは、ある課題T(Task)について、ある性能基準P(performance)に基づき、もしTについての性能が基準Pで測定して、経験E(Experience)と共に改善している場合に、 経験Eから学習したと言うことが出来る。
こちらはやや最近の定義だそうです。将棋を例に挙げて説明してみると、
E=多くの将棋対戦を行った経験
T=将棋の試合
P=次の試合に勝つ確率
というように分かれます。この例でもよく分からなかったのですが
ざっくりとEが過去の事象、Tが現在の事象、Pが未来の事象のように解釈しました。
機械学習は大きく教師あり学習と教師なし学習に分類されます。
教師あり学習(Supervised Learning)
あるデータにおいてインプットとアウトプットの関係が明らかな場合、その課題は教師あり学習と呼ばれます。ざっくり言うと答え付きの問題を解いて学習していく方法です。
教師あり学習は回帰問題と分類問題に分かれています。
1)回帰問題(regression)
入力変数を連続関数にマッピングする。
ex)ある人の顔写真から年齢を予測する。
2)分類問題(classification)
入力変数を別々のカテゴリにマッピングする。
ex)腫瘍のある患者が良性か悪性かを判断する。
教師なし学習(Unsupervised Learning)
データに含まれる変数同士の関係を仮定せず、そのデータの構造を決定するとき、その課題は教師なし学習と呼ばれます。答えが分からない問題をいくつかの情報から自動的に学習する方法です。代表的な例としてクラスタリングがあります。
クラスタリング(Clustering)
1,000,000個の異なる遺伝子の集まりを取り、これらの遺伝子を寿命、位置、役割などのさまざまな変数によって類似または関連するグループに自動的にグループ化する方法を見つける。
モデル表現
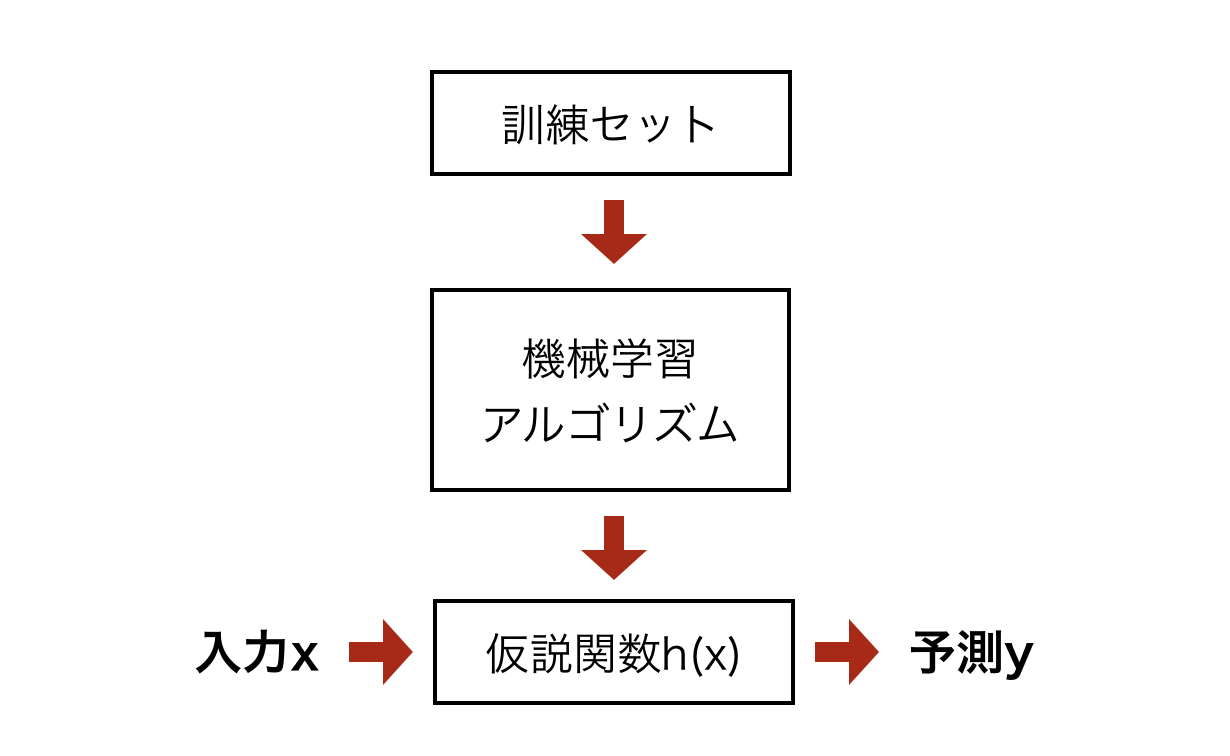
大雑把ではありますが上記が教師あり学習のモデル図を表したものです。ある訓練セットが与えられたとき、入力xから出力yを導く仮説関数h(x)を学習することが目的となります。
仮説関数(Hypothesis function)
上記のモデルで出てきた仮説関数は最も簡単な形では以下のように定義されます。
\hat{y}=h_\theta(x) = \theta_0 + \theta_1x
上記の仮説関数が何を表しているかと言うと入力 $x$を受け取った時の出力の予測値 $\hat{y}$を求める関数です。そして、$\theta_0,\theta_1$は重みづけのための係数です。機械学習アルゴリズムでこの$\theta$を最適化することで入力から正しい予測値を導くことができるようになります。
ちなみにこの『仮説』と言う名称は機械学習の初期に使われており、それがなんとなく定着してしまったものだそうです。なのでしっくりこなくてもあまり気にしなくて良いそうです。
コスト関数(Cost function)
コスト関数とは仮説関数$h_\theta$がどれだけデータにフィットしているかを計算する関数です。この関数が示す値が小さいほど予測が正しいと言えます。
以下にコスト関数の一般的な例を示します。
J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^{n}(\hat{y}_i−y_i)^2=\frac{1}{2m}\sum_{i=1}^{n}(h_\theta(x_i)−y_i)^2
そもそも学習の目標は、入力$x$に対する正しい出力$y$に予測値$\hat{y}$を近づけることです。そのためにはn個のデータがある場合、それぞれの$\hat{y}$と$y$の誤差を出してn個分の誤差を合計したものを可能な限り少なくしていけば良いわけです。ただし単純に$\sum_{i=1}^{n}(\hat{y}-y)$とすると、誤差が正の場合と負の場合で打ち消しあってしまう可能性があります。そこで二乗和を取ることで符号に関係なく誤差を評価できます。
$\frac{1}{2}$が付いている理由は、後ほどこの式を微分するのですがその時に都合がいいためです。
最急降下法(Gradient Descent)
最急降下法とは、コスト関数を最小にするための方法です。
この方法を上手く利用することでコスト関数を小さくしていき、最適な$\theta$の値を求めることができます。
\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta}J(\theta_j)
上記のような方法で$\theta$の値を更新していきます。
$:=$は更新・上書きと言う意味です。$\alpha$は学習率 (learning rate)と呼ばれます。名前の通りどのくらいのペースで学習するかと言うことを表しています。

$\frac{\partial}{\partial\theta}J(\theta_j)$はコスト関数の偏微分を表しています。
$\frac{\partial}{\partial\theta}J(\theta)<0$ の場合、正の方向にが更新され、$\frac{\partial}{\partial\theta}J(\theta)>0$ の場合、負の方向に更新されます。
最急降下法を繰り返していくことで徐々に最小値に近づいていき、最小値になると偏微分は0となり更新がストップします。このようにして最小値を探索しています。
まとめ
①機械学習は教師あり学習と教師なし学習に分類される。
②まず仮説関数を作り、コスト関数で出力と予測値の誤差を求める
③コスト関数を最小にするために最急降下法を用いて$\theta$を更新していく。
おわりに
講義で学んだことを整理することで講義の時には理解できていなかった部分も理解できました。ただまとめるのに結構時間がかかるので、次回からは重要な部分を重点的にまとめていこうと思います。