More than 1 year has passed since last update.

CNN高速化シリーズ ~FCNN: Fourier Convolutional Neural Networkの導入~

Last updated at 2022-12-05Posted at 2020-10-19

概要

畳み込みニューラルネットワーク(CNN)の登場により画像認識の分野は大きく進展しました。
AlexNetから始まりVGGNetやGoogLeNetなどの様々なネットワークが提案されその効果を示してきました。
そんなCNNですが、畳み込み演算の処理が重いため非常に時間がかかってしまうことが難点として挙げられます。その重さは全結合層を完全に無視できてしまうほどで、畳み込み処理を高速化することができれば学習時間を大幅に削減することが可能となります。
そこで注目されているのが空間領域での畳み込み=周波数空間での要素積という関係です。
本記事では周波数領域で畳み込みを行う上での基礎理論について説明します。
日本語の記事はほとんど見当たらなかったので論文から頑張って読み解いています。間違いや勘違いなど散見されるかもしれませんのでぜひご指摘ください。

本記事で取り扱う論文は

Fast Training of Convolutional Networks through FFTs; Michael Mathieu, Mikael Henaff, Yann LeCun; arXiv:1312.5851v5 [cs.CV] 6 Mar 2014

です。

畳み込みとは

周波数領域での畳み込みを正しく理解するためにも、まずは空間領域での畳み込みというものについて改めて考えてみます。
畳み込み処理には2種類あり、それぞれ 線形畳み込み(直線畳み込み) と 循環畳み込み(巡回畳み込み) と呼ばれています。まずはこの二つについて説明します。

以降使用する変数を先に紹介しておきます。

$I \cdots$入力サイズ
$F \cdots$フィルタサイズ
$O \cdots$出力サイズ

線形畳み込み

線形畳み込みは下図のように表される畳み込み処理のことです。

このように、フィルタの右端と入力の左端とが重なる地点からスタートし、通り抜けたら終了するような感じです。
数学的な式は別に不要なので載せませんが、こういう動作をしていることは理解しておいてください。
そして、この線形畳み込みは入力が周期関数ではないことに注意してください。

また、サイズについては次のような関係式が成り立ちます。

O = I + F - 1

GIFでは$I = 9$及び$F = 3$ですので、出力サイズは$O = 9 + 3 - 1 = 11$となります。

循環畳み込み

循環畳み込みは下図のように表される畳み込み処理のことです。

こちらはフィルタの左端と入力の左端とが重なる地点からスタートし、フィルタの右端と入力の右端が重なったら終了するような感じですね。
線形畳み込みとの違いはまさにこれで、この場合入力は周期関数である必要があります。
線形畳み込みのGIFで表されている両端それぞれ2つ分は入力が周期関数であるから必要ない、みたいな理解で良いと思います(厳密には異なると思いますが厳密さは特に求めていないので)。

また、サイズについては以下の関係式が成り立ちます。

O = I - F + 1

GIFでは$I = 9$及び$F = 3$ですので、出力サイズは$O = 9 - 3 + 1 = 7$となります。

線形畳み込みと循環畳み込みを等しくする方法

線形畳み込みと循環畳み込みを等しくするためには、入力の両端に$O = I + F - 1$になるようにゼロパディングを施す必要があります。

出力結果が線形畳み込みと等しくなっていることが確認できますね。

CNNでの畳み込み

さて、CNNでの畳み込み演算はどちらに当てはまるのでしょうか？入力の観点から考えてみます。

CNNに入力されるデータは通常画像であり、その画像とは写真であることが大多数でしょう。よって、パターン模様の画像認識をするのではない場合画像は周期性を持たないことが予想できます。
ということは、入力が非周期的であるためCNNは線形畳み込みを行う必要がありますね。

しかし、まだこれを結論とするには早いです。下図を御覧ください。

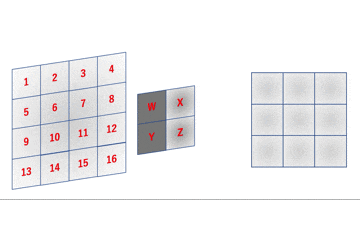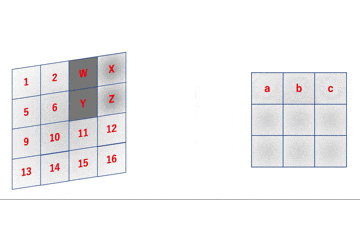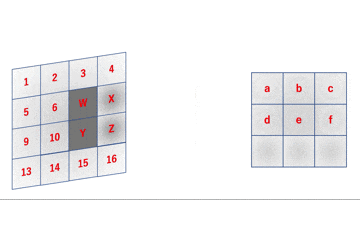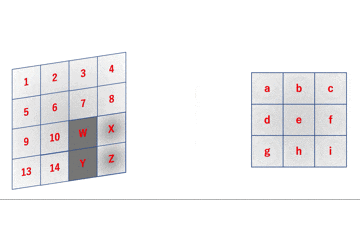
こちらはCNNの畳み込みの様子を表しています。ご覧の通り、フィルタは入力画像を通り過ぎたりしていませんので、この図では循環畳み込みを行っていることになります。これではせっかくの畳み込み演算から正しく情報を得ることができていないことになります。
ただし、入力画像が上下左右に($F - 1$だけ重なって)周期的に配置されていると仮定すればこの畳み込みを正しいと見做すことはできます。

「結局どっちなんだ」と言いたいですがまだ考えることがあります。それはCNNに必須の技術であるパディングです。

この図だと数が足りませんが、必要数だけパディングを施せば循環畳み込みは線形畳み込みに等しくすることができるんでしたね。すると、パディングという処理を入力画像に正しく施せば線形畳み込みをすることができ、畳み込み演算から正しく情報を得ることができるというわけです。
以前書いた記事でパディングの役目を「サイズ維持」と「端の情報を余さず得る」としていますが、これはそういうことです。(執筆当時はそんなこと露ほども考えてませんでしたが笑)

さて、このパディングという処理のせいで一層議論がややこしくなります。CNNでの畳み込み特有のストライドも考慮するとより一層...
このパディング、CNNでの畳み込みによる出力画像のサイズ減衰を防ぐ(あるいは軽減する)ために用いられることが多いです。よって、パディング幅はストライドに依存して増減するので、循環畳み込みを線形畳み込みにしたいとは全く考えていないわけです。
するとパディング幅に過不足が生じます。パディング幅が多い分には問題ないのですが、少ない場合は正しく循環畳み込み$\rightarrow$線形畳み込みへの変換が行われなくなることになります。

結局のところ、結論としては 「CNNでの畳み込みは線形/循環畳み込みの中間」 といったところでしょうか。
「これだけ引っ張っておいて結論が曖昧かよ」とつっこみたいですが、まあそうとしか言えないので仕方ないでしょう。
理論的に厳密な議論をするとなると、実は前提から異なりますしね。

ここまでが前提になります。ここからいよいよ周波数領域での理論に移ります。
ちなみに「数学的な厳密さは？」と思った方は付録の方をご覧ください。

周波数領域へ

さて、ここまでの話はぼくが論文を読んでいる中で必要かなと感じてあちこちで調べた結果を要約したものです。まだまだ甘いですが、まあこれぐらいの話が頭に入っていれば大丈夫だと思います。
それではいよいよ論文の内容に入ります。論文2.1のBackpropagationは空間領域でのCNNと周波数領域でのCNNとを比較する部分を述べているだけなのでカットして、2.2から読んでいきます。
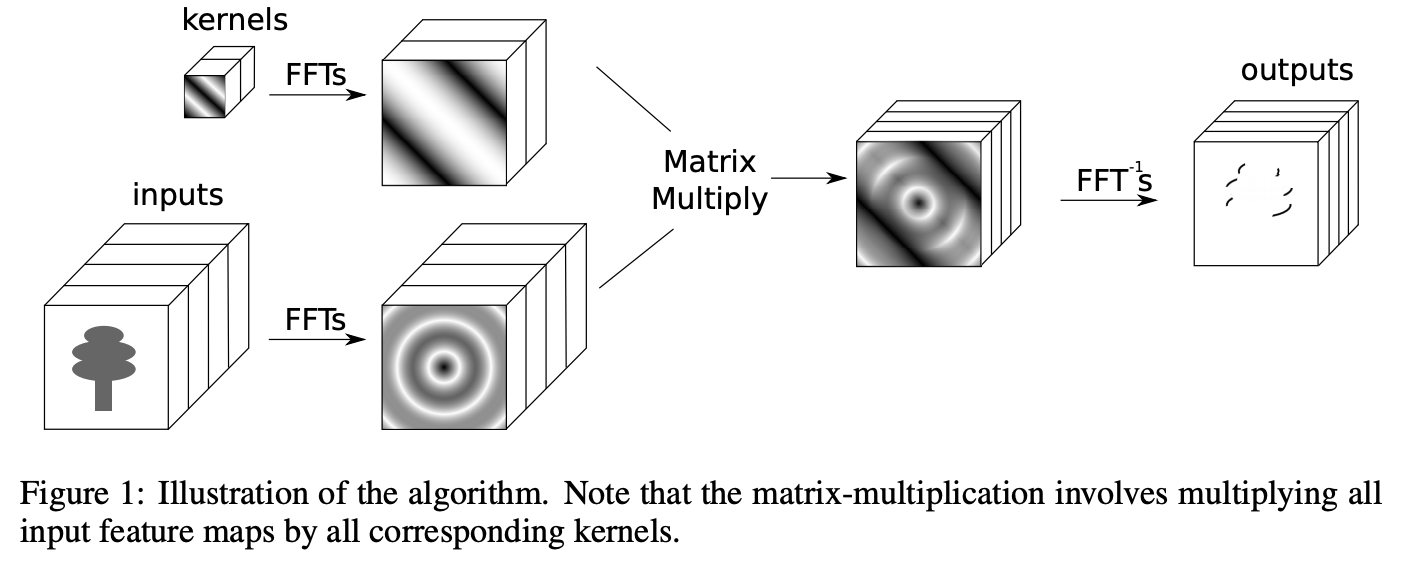
ちなみに論文の和訳ではなく意訳や追記をしています。なお、この節の図は論文から引用させていただいています。

2.2 アルゴリズム

空間領域での畳み込み演算はフーリエ(周波数)領域での要素積と等価であることはよく知られています。そのため、空間領域での畳み込み演算はフーリエ変換器$\mathcal{F}$とその逆演算$\mathcal{F}^{-1}$を用いて

f * g = \mathcal{F}^{-1}\big(\mathcal{F}_f(k) \odot \mathcal{F}_g(k)\big)

と表すことができます。ただし、記号$ * $は空間領域での畳み込み演算を、記号$\odot$は行列演算における要素積を表します。
注意しなければならないのは、上式の演算を行うには要素積の性質上 $f,g$が近しいサイズ(というより等しいサイズ)である必要がある ということです。
しかし一般に入力(サイズ$I_h \times I_w$)とフィルタ(サイズ$F_h \times F_w$)とは全く異なるサイズになっています。そのため、実装する際は入力やフィルタのサイズを揃えるようにパディングが必要になります。(トリミングすることもあるかもしれません)

議論の簡単のために、$I_h = I_w = I$および$F_h = F_w = F$とします。また、出力のサイズは$O_h \times O_w$とし、これも$O_h = O_w = O$と表すことにします。また、入力のチャンネル数を$C$、フィルタの枚数を$M$、ミニバッチのサイズを$B$としておきます。
空間領域での畳み込み演算の計算量はパディングなし、ストライド$1$だと

O^2 F^2 \quad (\because O = I - F + 1)

となります。パディング幅$2p$、ストライド$s$とすると

O^2 F^2 \quad \left(\because O = \left\lceil \cfrac{I - F + 2p}{s} \right\rceil + 1 \right)

ですね。

一方、フーリエ領域での計算量はフーリエ変換を 高速フーリエ変換(FFT: Fast Fourier Transformation) で行った場合$$2C_{order}O^2 \log{O}$$で、要素積の計算量は、複素数演算であることに注意すると$$4O^2$$と表されます。$C_{order}$は定数です。
よって、その和の$$2C_{order}O^2 \log{O} + 4O^2$$がフーリエ領域での畳み込み演算の計算量ということになります。
論文では$O = I$としているみたいです。

各入力チャンネルやフィルタは独立しているため、それぞれに1度フーリエ変換を施すだけで済みます。特定の畳み込みに関しては学習効率が低下する可能性はありますが、FFTを効果的に再利用することが可能なため、効率低下によるオーバーヘッドを補う以上の恩恵を得ることができます。

順伝播や逆伝播について計算量を求めると、フーリエ領域での畳み込み演算の優位性がより明白になります。

	空間領域	フーリエ領域
$\displaystyle\sum_{C}{x_C * F_{CM}}$	$BCMO^2F^2$	$2C_{order}I^2(BM + BC + CM)\log{I} + 4BCMI^2$
$\cfrac{\partial L}{\partial y_M} * w^{\top}_{CM} $	$BCMI^2F^2$	$2C_{order}O^2(BM + BC + CM)\log{O} + 4BCMO^2$
$\cfrac{\partial L}{\partial y_M} * x_C$	$BCMO^2F^2$	$2C_{order}I^2(BM + BC + CM)\log{I} + 4BCMI^2$

注意すべきは、ここでの$O$は空間領域・周波数領域両方とも$$O = I - F + 1$$または$$O = \left\lceil \cfrac{I - F + 2p}{s} \right\rceil + 1 $$で計算されるものである、ということです。特にフーリエ領域においては先の議論と異なっていることに注意してください。
おそらく計算量の比較を正しく行うために揃えたのだと思われます。

この表から読み取れることとして、空間領域での計算量は5つの項の積で表されているのに対してフーリエ領域での計算量は最大4つの項の積で表されている、ということです。
ざっくりいうと空間領域では計算量のオーダが5次(より正確には7次)、フーリエ領域では4次(より正確には5次)である、というわけです。

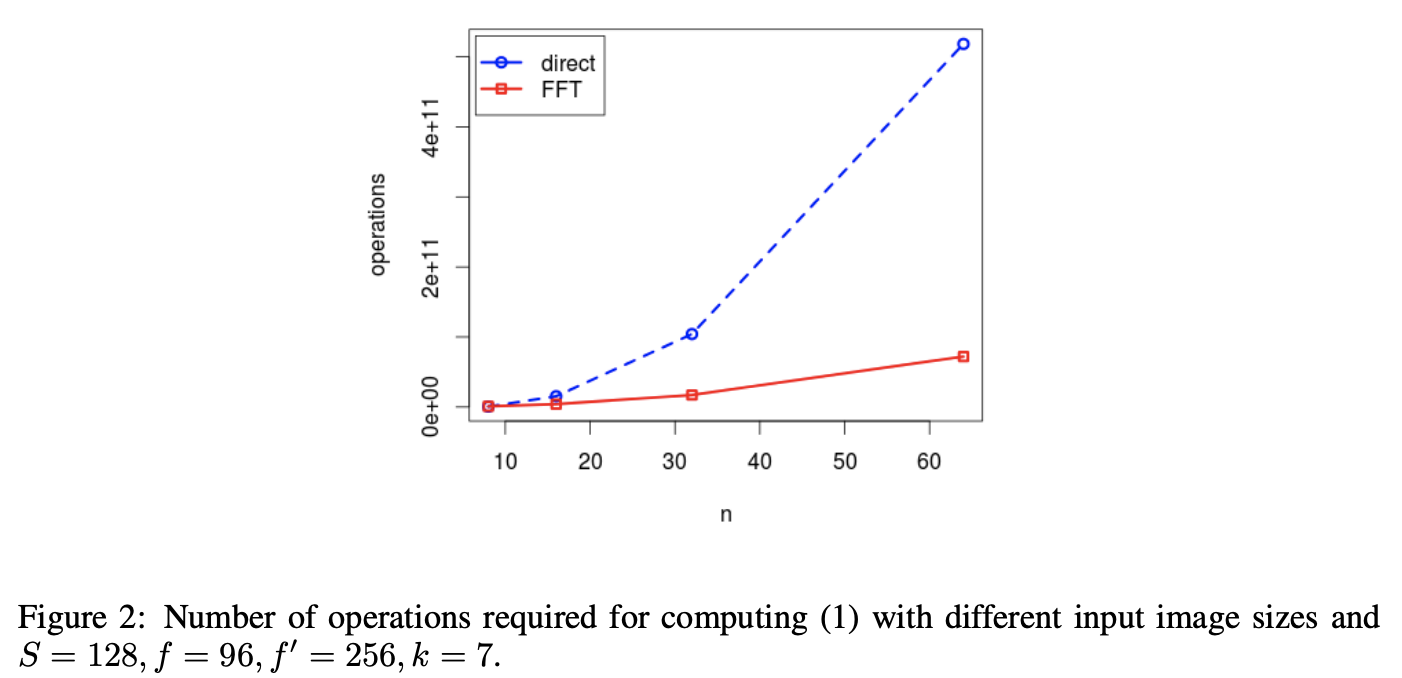
これがどれくらいの効果を生むのか実際に順伝播について計算して確かめてみましょう。

B = 128 \quad C = 96 \\
M = 256 \quad F = 7

として、$I = 16, 64$の二つを計算してみると、$O = I - F + 1 = 10, 58$であるから、空間領域について

BCMO^2F^2 = 128 \times 96 \times 256 \times 10^2 \times 7^2 = 15,414,067,200 \simeq 154億 \\
BCMO^2F^2 = 128 \times 96 \times 256 \times 58^2 \times 7^2 = 518,529,220,608 \simeq 5185億

フーリエ領域について

2C_{order}I^2(BM + BC + CM)\log{I} + 4BCMI^2 = 2 \times 16 \times 16^2 \times (128 \times 256 + 128 \times 96 + 96 \times 256) \log{16} + 4 \times 128 \times 96 \times 256 \times 16^2 = 1,581,554,875.654148 + 3,221,225,472 = 4,802,780,347.654148 \simeq 48億 \\
2C_{order}I^2(BM + BC + CM)\log{I} + 4BCMI^2 = 2 \times 16 \times 64^2 \times (128 \times 256 + 128 \times 96 + 96 \times 256) \log{64} + 4 \times 128 \times 96 \times 256 \times 64^2 = 37,957,317,015.69955 + 51,539,607,552 = 89,496,924,567.69955 \simeq 895億

※論文中に$C_{order}$をいくらとして計算したかが載っていないので、グラフと概ね一致する$C_{order} = 16$を採用しました。

という感じで、入力のサイズが大きくなるにつれてどんどん差が広がっていきます。

2.3 実装と空間計算量

アルゴリズムとしては非常に単純なフーリエ領域での畳み込み演算ですが、実装に際して大きく2つの問題点が存在します。

現行のGPU、主にNVIDIA製のGPUに対応するCUDAで実装されているFFTは大きな入力で限られた数だけFFTするのに最適化されているため、本アルゴリズムにおいては最適ではない
フーリエ変換されたフィルタを保持するために多量のメモリ領域(空間計算量)が必要となる

それぞれの問題に対しては以下のような最適化・対応策が提案されています。

Cooley-Turkey FFTアルゴリズムを実装
- ミニバッチ・チャンネル方向に並列化可能に
- もともと2次元FFTは行方向と列方向に並列化可能
- 以上から本アルゴリズムでの小規模かつ大量の入力を効率的かつ高速にフーリエ変換できる
各畳み込みで使用するメモリを使い回す(上書きする)ことで省メモリ化。また、実数値入力のフーリエ変換が対称行列となることを利用して、下三角行列(または上三角行列)のみ保持する
- メモリを使い回すため、逆伝播の計算の際に再FFTが必要になる
- 三角行列で保持することで保持すべきメモリ量は$X^2 \Rightarrow \frac{X(X + 1)}{2}$に

これで理論面は終了です。あとは実験結果とかですね。
もうちょっと具体的にどういう演算で計算が進んでいるのか載せて欲しかったです...実装しようとした段階でいくつか疑問点も出てきましたし...まあその辺りは通常のCNNと似た動作をするようにすればいいんでしょうが。

3 実験

実験はCUDAConv GPU実装とTorch7機械学習環境を比較対象として、NVIDIA製のGeForce GTX TitanGPUを使用して行われました。
実験で得られた精度は載せられていませんが、許容誤差範囲内の差しかなかったようです。

あるCNNの、入力チャンネル数$C = 96$、出力チャンネル数(つまりフィルタ枚数)$M = 256$である第2層に注目して、そのレイヤのフィルタサイズ・入力サイズ・ミニバッチサイズを変更した実験結果は下図の通りとなっています。

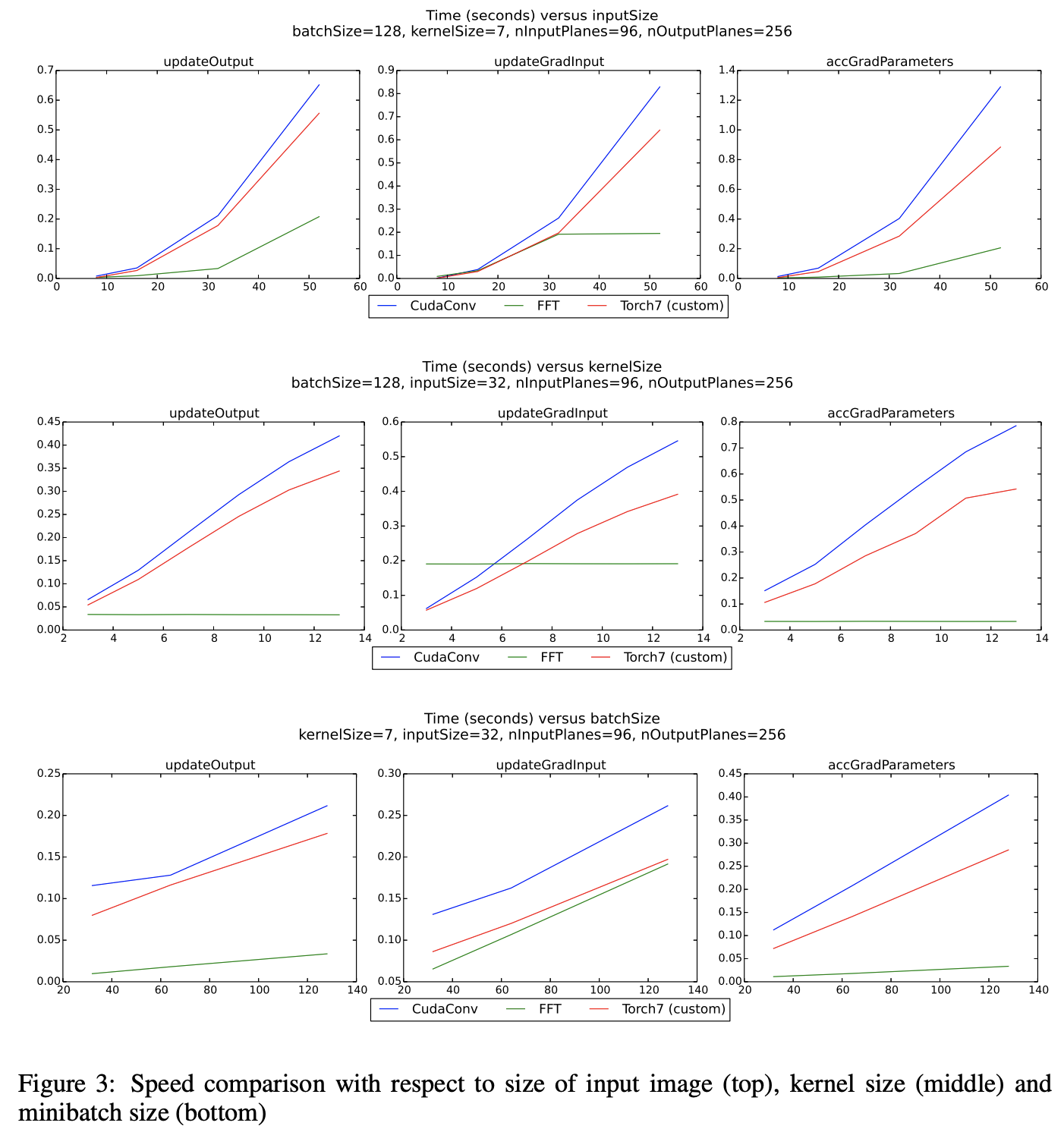
ほとんどの場合でフーリエ領域での畳み込み演算が高速に動作していることが示されています。特に時間計算量が大きい$$\cfrac{\partial L}{\partial y_M} * x_C $$においてより顕著な優位性が認められます。
これは、フィルタサイズが大きいものを利用しているためである可能性が高いと考えられています。
また、FFT適用前にフィルタは入力と同サイズまでパディングされるため、より大きなフィルタを利用しても良いということになります。

※この考察についてですが、現行のCNNの多くが小さなフィルタサイズを利用しているのは省メモリの観点からだったりします。
確かにFCNNの実装がこのままであればどうせ大量のメモリを消費するので、いっそのこと大きなフィルタを使うのはアリかもしれません。
ちなみにこのままの実装が用いられることは多分ありません。しっかり別の省メモリ技術が確立されています。
そちらについてはまた別の記事を書きます。

続いて、先ほどは第2層にのみ注目していたCNNについて、今度は第1層〜第5層までに注目して、ミニバッチサイズ$B$を変更して実験した結果を下図に示します。

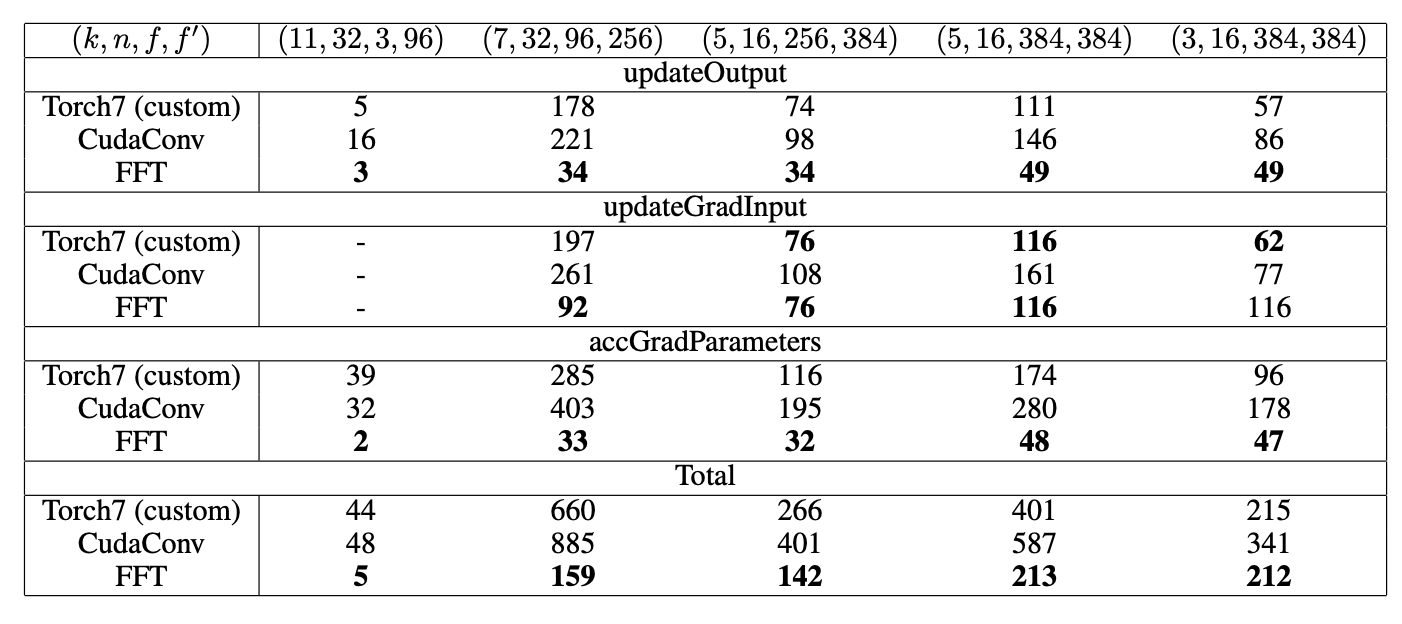
なお、入力層の入力への勾配は計算する必要がないためデータが取られていません。
ほとんどの場合で最速か次点くらいの速度を誇っていることが読み取れます。また、トータルで見ると全て最速であるためFCNNがほぼ全ての場合で有効であることが言えます。
また、順伝播がかなり高速となっており、これは学習済みネットワークを用いて推論を行うときなどに最大限その恩恵を得られるということを示唆しています。

最後に、上記のCNNにプーリングレイヤと全結合層を追加した時の実験結果です。この実験はパディングやメモリへのアクセスなどの実装の詳細によってパフォーマンスが変化するかを確認するためのものです。

この実験においてもFCNNはその優位性を証明してみせました。

4 今後について

箇条書きにしておきます。

フーリエ領域内でフィルタを直接学習する方法を探る
フーリエ領域内で非線形関数を使用する方法を探る
- これにより逆変換の必要がなくなり、より高速に
現在の実装では入力画像を2の累乗のサイズになるようにパディングする必要があるため、これを改良する
フィルタサイズを大きくしたときの影響を調べる

以上が論文の内容になります。シンプルながら強力なアルゴリズムですね〜
これ以降様々な研究がされているようです。

実装してみる?

実装してみたい...のですが、いくつか疑問があります。

畳み込み演算の前後でFFT・IFFTする必要がある？
論文の模式図では入力チャンネル数と出力チャンネル数が揃っているが、空間領域での畳み込み層の出力チャンネル数はフィルタの枚数に依存しているはず
また、チャンネル数をどちらに合わせるにせよ、どうやってその次元に揃えるかが問題

それぞれ論文の中で明記されてない...はずですが、微妙に読み取れたりもするんですよね〜
例えば4 今後についてで

フーリエ領域内でフィルタを直接学習する方法を探る

フーリエ領域内で非線形関数を使用する方法を探る
- これにより逆変換の必要がなくなり、より高速に

みたいなことを言っているので、行列積演算の前後でのみFFT/IFFTしてるっぽいとか、実験の最後の表でチャンネル数がCNNと同じように変化しているとか、直接書いてはいないけど多分そうだと思える記述が見受けられます。

あと、後発論文とかいくつか探して読んでみたりしていますが、そっちではFFTを最初の1回で済ませて、全てフーリエ領域で実行する手段についての記述も見受けられましたので、その辺りも含めてまだまだ勉強不足のため今回は実装を見送ります。フーリエ変換についてもまだ理解不足感が否めませんしね〜

付録

おまけとして数学的なことを載せておきます。

厳密な畳み込みとCNN

次のような入力行列$\boldsymbol{A}$とフィルタ行列$\boldsymbol{W}$の畳み込みを考えます。ただし、パディングなし、ストライド$1$とします。
※以降の行列要素のインデックスとか間違ってたらごめんなさい

\boldsymbol{A} = \left( \begin{array}[ccc]
  aa_{1, 1} & a_{1, 2} & a_{1, 3} & a_{1, 4} \\
  a_{2, 1} & a_{2, 2} & a_{2, 3} & a_{2, 4} \\
  a_{3, 1} & a_{3, 2} & a_{3, 3} & a_{3, 4} \\
  a_{4, 1} & a_{4, 2} & a_{4, 3} & a_{4, 4}
\end{array} \right) \qquad
\boldsymbol{W} = \left( \begin{array}[ccc]
  ww_{1, 1} & w_{1, 2} \\
  w_{2, 1} & w_{2, 2} \\
\end{array} \right)

これの畳み込み結果は次のようになります。

\begin{align}
  \boldsymbol{AW} &= \left( \begin{array}[ccc]
    aa_{1, 1}w_{1, 1} + a_{1, 2}w_{1, 2} + a_{2, 1}w_{2, 1} + a_{2, 2}w_{2, 2}
  & a_{1, 2}w_{1, 1} + a_{1, 3}w_{1, 2} + a_{2, 2}w_{2, 1} + a_{2, 3}w_{2, 2}
  & a_{1, 3}w_{1, 1} + a_{1, 4}w_{1, 2} +   a_{2, 3}w_{2, 1} + a_{2, 4}w_{2, 2} \\
    a_{2, 1}w_{1, 1} + a_{2, 2}w_{1, 2} + a_{3, 1}w_{2, 1} + a_{3, 2}w_{2, 2}
  & a_{2, 2}w_{1, 1} + a_{2, 3}w_{1, 2} + a_{3, 2}w_{2, 1} + a_{2, 3}w_{2, 2}
  & a_{2, 3}w_{1, 1} + a_{2, 4}w_{1, 2} + a_{3, 3}w_{2, 1} + a_{2, 4}w_{2, 2} \\
    a_{3, 1}w_{1, 1} + a_{3, 2}w_{1, 2} + a_{4, 1}w_{2, 1} + a_{4, 2}w_{2, 2}
  & a_{3, 2}w_{1, 1} + a_{3, 3}w_{1, 2} + a_{4, 2}w_{2, 1} + a_{4, 3}w_{2, 2}
  & a_{3, 3}w_{1, 1} + a_{3, 4}w_{1, 2} + a_{4, 3}w_{2, 1} + a_{4, 4}w_{2, 2}
  \end{array} \right) \\
  &= \left( \begin{array}[ccc]
    s\displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k, l}w_{k, l}}}
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k, l+1}w_{k, l}}}
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k, l+2}w_{k, l}}} \\
    \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+1, l}w_{k, l}}} 
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+1, l+1}w_{k, l}}}
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+1, l+2}w_{k, l}}} \\
    \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+2, l}w_{k, l}}}
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+2, l+1}w_{k, l}}}
  & \displaystyle\sum_{k=1}^{2}{\displaystyle\sum_{l=1}^{2}{a_{k+2, l+2}w_{k, l}}}
  \end{array} \right)
\end{align}

規則性が見えると思います。では一般化してみましょう。
フィルタサイズを$F_h \times F_w$としたとき、出力の$(i, j)$成分$o_{i, j}$は

o_{i, j} = \displaystyle\sum_{k=1}^{F_h}{\displaystyle\sum_{l=1}^{F_w}{a_{i+k-1, j+l-1}w_{k, l}}}

と書くことができます。後々のために添え字の足し算の順序を変えていますので注意してください。

これがCNNでの畳み込み演算となります。循環畳み込みですね。
ところで、数学的には2次元離散畳み込み演算は次式で表されます。

(g * f)_{i, j} = o_{i, j} = \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{i-k+1, j-l+1}g_{k, l}}}

なんとなく$f$を入力、$g$をフィルタと見做して、一般的な式とは逆順にしてあります。また、$k, l$はインデックスが有効になる全ての値を取ります。
この時点で「あれ？」と思った方は鋭いです。
これは行列で書くと(サイズはそれぞれCNNの時に揃えます)

\begin{align}
  \boldsymbol{g*f} &=　\left(
  \begin{array}[ccccc]
    s\displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{2-k, 2-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{2-k, 3-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{2-k, 4-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{2-k, 5-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{2-k, 6-l}g_{k, l}}} \\
    \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{3-k, 2-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{3-k, 3-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{3-k, 4-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{3-k, 5-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{3-k, 6-l}g_{k, l}}} \\
    \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{4-k, 2-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{4-k, 3-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{4-k, 4-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{4-k, 5-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{4-k, 6-l}g_{k, l}}} \\
    \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{5-k, 2-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{5-k, 3-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{5-k, 4-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{5-k, 5-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{5-k, 6-l}g_{k, l}}} \\
    \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{6-k, 2-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{6-k, 3-l}g_{k, l}}}
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{6-k, 4-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{6-k, 5-l}g_{k, l}}} 
  & \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{6-k, 6-l}g_{k, l}}}
  \end{array} \right) \\
  &= \left(
  \begin{array}[ccccc]
    ff_{1, 1}g_{1, 1}
  & f_{1, 2}g_{1, 1} + f_{1, 1}g_{1, 2}
  & f_{1, 3}g_{1, 1} + f_{1, 2}g_{1, 2}
  & f_{1, 4}g_{1, 1} + f_{1, 3}g_{1, 2}
  & f_{1, 4}g_{1, 2} \\
    f_{2, 1}g_{1, 1} + f_{1, 1}g_{2, 1}
  & f_{2, 2}g_{1, 1} + f_{2, 1}g_{1, 2} + f_{1, 2}g_{2, 1} + f_{1, 1}g_{2, 2}
  & f_{2, 3}g_{1, 1} + f_{2, 2}g_{1, 2} + f_{1, 3}g_{2, 1} + f_{1, 2}g_{2, 2}
  & f_{2, 4}g_{1, 1} + f_{2, 3}g_{1, 2} + f_{1, 4}g_{2, 1} + f_{1, 3}g_{2, 2}
  & f_{2, 4}g_{1, 2} + f_{1, 4}g_{2, 2} \\
    f_{3, 1}g_{1, 1} + f_{2, 1}g_{2, 1}
  & f_{3, 2}g_{1, 1} + f_{3, 1}g_{1, 2} + f_{2, 2}g_{2, 1} + f_{2, 1}g_{2, 2}
  & f_{3, 3}g_{1, 1} + f_{3, 2}g_{1, 2} + f_{2, 3}g_{2, 1} + f_{2, 2}g_{2, 2}
  & f_{3, 4}g_{1, 1} + f_{3, 3}g_{1, 2} + f_{2, 4}g_{2, 1} + f_{2, 3}g_{2, 2}
  & f_{3, 4}g_{1, 2} + f_{2, 4}g_{2, 2} \\
    f_{4, 1}g_{1, 1} + f_{3, 1}g_{2, 1}
  & f_{4, 2}g_{1, 1} + f_{4, 1}g_{1, 2} + f_{3, 2}g_{2, 1} + f_{3, 1}g_{2, 2}
  & f_{4, 3}g_{1, 1} + f_{4, 2}g_{1, 2} + f_{3, 3}g_{2, 1} + f_{3, 2}g_{2, 2}
  & f_{4, 4}g_{1, 1} + f_{4, 3}g_{1, 2} + f_{3, 4}g_{2, 1} + f_{3, 3}g_{2, 2}
  & f_{4, 4}g_{1, 2} + f_{3, 4}g_{2, 2} \\
    f_{4, 1}g_{2, 1}
  & f_{4, 2}g_{2, 1} + f_{4, 1}g_{2, 2}
  & f_{4, 3}g_{2, 1} + f_{4, 2}g_{2, 2}
  & f_{4, 4}g_{2, 1} + f_{4, 3}g_{2, 2}
  & f_{4, 4}g_{2, 2}
  \end{array} \right) \\
\end{align}

となります。

こうしてみると一目瞭然ですが、CNNでの畳み込みと数学で定義されている畳み込みは異なります。この差異は循環畳み込みと線形畳み込みとの違い...と思ったら実は違います。
先に紹介した線形畳み込みと循環畳み込みを等しくする方法のようにパディングを施しても同じにはなりません。
実際に試してみます。

\boldsymbol{A} = \left( \begin{array}[cccccc]
  00 & 0 & 0 & 0 & 0 & 0 \\
  0& a_{1, 1} & a_{1, 2} & a_{1, 3} & a_{1, 4} & 0 \\
  0 & a_{2, 1} & a_{2, 2} & a_{2, 3} & a_{2, 4} & 0 \\
  0 & a_{3, 1} & a_{3, 2} & a_{3, 3} & a_{3, 4} & 0 \\
  0 & a_{4, 1} & a_{4, 2} & a_{4, 3} & a_{4, 4} & 0 \\
  0 & 0 & 0 & 0 & 0 & 0
\end{array} \right)

として、

\boldsymbol{AW} = \left(
  \begin{array}[ccccc]
    aa_{1, 1}w_{2, 2}
  & a_{1, 1}w_{2, 1} + a_{1, 2}w_{2, 2}
  & a_{1, 2}w_{2, 1} + a_{1, 3}w_{2, 2}
  & a_{1, 3}w_{2, 1} + a_{1, 4}w_{2, 2} 
  & a_{1, 4}w_{2, 1} \\
    a_{1, 1}w_{1, 2} + a_{2, 1}w_{2, 2}
  & a_{1, 1}w_{1, 1} + a_{1, 2}w_{1, 2} + a_{2, 1}w_{2, 1} + a_{2, 2}w_{2, 2}
  & a_{1, 2}w_{1, 1} + a_{1, 3}w_{1, 2} + a_{2, 2}w_{2, 1} + a_{2, 3}w_{2, 2}
  & a_{1, 3}w_{1, 1} + a_{1, 4}w_{1, 2} + a_{2, 3}w_{2, 1} + a_{2, 4}w_{2, 2}
  & a_{1, 4}w_{1, 1} + a_{2, 4}w_{2, 1} \\
    a_{2, 1}w_{1, 2} + a_{3, 1}w_{2, 2}
  & a_{2, 1}w_{1, 1} + a_{2, 2}w_{1, 2} + a_{3, 1}w_{2, 1} + a_{3, 2}w_{2, 2}
  & a_{2, 2}w_{1, 1} + a_{2, 3}w_{1, 2} + a_{3, 2}w_{2, 1} + a_{3, 3}w_{2, 2}
  & a_{2, 3}w_{1, 1} + a_{2, 4}w_{1, 2} + a_{3, 3}w_{2, 1} + a_{3, 4}w_{2, 2}
  & a_{2, 4}w_{1, 1} + a_{3, 4}w_{2, 1} \\
    a_{3, 1}w_{1, 2} + a_{4, 1}w_{2, 2}
  & a_{3, 1}w_{1, 1} + a_{3, 2}w_{1, 2} + a_{4, 1}w_{2, 1} + a_{4, 2}w_{2, 2}
  & a_{3, 2}w_{1, 1} + a_{3, 3}w_{1, 2} + a_{4, 2}w_{2, 1} + a_{4, 3}w_{2, 2}
  & a_{3, 3}w_{1, 1} + a_{3, 4}w_{1, 2} + a_{4, 3}w_{2, 1} + a_{4, 4}w_{2, 2}
  & a_{3, 4}w_{1, 1} + a_{4, 4}w_{2, 1} \\
    a_{4, 1}w_{1, 2}
  & a_{4, 1}w_{1, 1} + a_{4, 2}w_{1, 2}
  & a_{4, 2}w_{1, 1} + a_{4, 3}w_{1, 2}
  & a_{4, 3}w_{1, 1} + a_{4, 4}w_{1, 2}
  & a_{4, 4}w_{1, 1}
  \end{array} \right)

となります。形状は一致しますし、各要素の足し算の数も一緒ですがインデックスが異なっていますね。
と、いうことはCNNの畳み込みは数学的に定義されている畳み込みとは別の演算ということになります。

これが本記事の畳み込みにおいてチラッと述べた

理論的に厳密な議論をするとなると、実は前提から異なりますしね。

のことです。そもそも 「CNNの畳み込みが数学的な畳み込みである」という前提が間違っていた のです。

「ではCNNの畳み込みは数学的にはどういう定義の処理に当たるのか、というか対応する数学的定義は存在するのか」という疑問があると思いますが、これについてはきちんと対応する数学的定義があります。相互関係です。

(g \star f)_{i, j} = o_{i, j} = \displaystyle\sum_{k}{\displaystyle\sum_{l}{f_{i+k-1, j+l-1}g_{k, l}}}

数学的な畳み込みと同じく、$k, l$は有効なインデックスとなる全ての値を取ります。これだとCNNの畳み込みと同じような定義ですので、同じ結果が得られることが想像できると思います。

この相互相関は二つの信号($f$と$g$)がどのくらい似ているのかを計算しています。あまり関係ないので詳しくは参考サイトに譲りますが、つまりCNNのフィルタは入力の特定パターンと似ている分布関数を学習していることになります。

ここで重要なのは相互相関をなんとか数学的な畳み込みに持っていけるのかどうかです。これまで当たり前のように畳み込み畳み込みと言っていた処理が実は畳み込みではありませんでした、では議論の根底から覆ってしまうことになり、全部考え直す必要が出てきてしまいます。一生懸命フィルタの解釈について考えてきた研究者の方々が泣いてしまいます...

改めてじっくり数学的な畳み込みとパディングを施した時のCNN畳み込みとを見比べてみましょう。

\left( \begin{array}[ccccc]
  ff_{1, 1}g_{1, 1}
& f_{1, 2}g_{1, 1} + f_{1, 1}g_{1, 2}
& f_{1, 3}g_{1, 1} + f_{1, 2}g_{1, 2}
& f_{1, 4}g_{1, 1} + f_{1, 3}g_{1, 2}
& f_{1, 4}g_{1, 2} \\
  f_{2, 1}g_{1, 1} + f_{1, 1}g_{2, 1}
& f_{2, 2}g_{1, 1} + f_{2, 1}g_{1, 2} + f_{1, 2}g_{2, 1} + f_{1, 1}g_{2, 2}
& f_{2, 3}g_{1, 1} + f_{2, 2}g_{1, 2} + f_{1, 3}g_{2, 1} + f_{1, 2}g_{2, 2}
& f_{2, 4}g_{1, 1} + f_{2, 3}g_{1, 2} + f_{1, 4}g_{2, 1} + f_{1, 3}g_{2, 2}
& f_{2, 4}g_{1, 2} + f_{1, 4}g_{2, 2} \\
  f_{3, 1}g_{1, 1} + f_{2, 1}g_{2, 1}
& f_{3, 2}g_{1, 1} + f_{3, 1}g_{1, 2} + f_{2, 2}g_{2, 1} + f_{2, 1}g_{2, 2}
& f_{3, 3}g_{1, 1} + f_{3, 2}g_{1, 2} + f_{2, 3}g_{2, 1} + f_{2, 2}g_{2, 2}
& f_{3, 4}g_{1, 1} + f_{3, 3}g_{1, 2} + f_{2, 4}g_{2, 1} + f_{2, 3}g_{2, 2}
& f_{3, 4}g_{1, 2} + f_{2, 4}g_{2, 2} \\
  f_{4, 1}g_{1, 1} + f_{3, 1}g_{2, 1}
& f_{4, 2}g_{1, 1} + f_{4, 1}g_{1, 2} + f_{3, 2}g_{2, 1} + f_{3, 1}g_{2, 2}
& f_{4, 3}g_{1, 1} + f_{4, 2}g_{1, 2} + f_{3, 3}g_{2, 1} + f_{3, 2}g_{2, 2}
& f_{4, 4}g_{1, 1} + f_{4, 3}g_{1, 2} + f_{3, 4}g_{2, 1} + f_{3, 3}g_{2, 2}
& f_{4, 4}g_{1, 2} + f_{3, 4}g_{2, 2} \\
  f_{4, 1}g_{2, 1}
& f_{4, 2}g_{2, 1} + f_{4, 1}g_{2, 2}
& f_{4, 3}g_{2, 1} + f_{4, 2}g_{2, 2}
& f_{4, 4}g_{2, 1} + f_{4, 3}g_{2, 2}
& f_{4, 4}g_{2, 2}
\end{array} \right) \\
\left( \begin{array}[ccccc]
    aa_{1, 1}w_{2, 2}
  & a_{1, 1}w_{2, 1} + a_{1, 2}w_{2, 2}
  & a_{1, 2}w_{2, 1} + a_{1, 3}w_{2, 2}
  & a_{1, 3}w_{2, 1} + a_{1, 4}w_{2, 2} 
  & a_{1, 4}w_{2, 1} \\
    a_{1, 1}w_{1, 2} + a_{2, 1}w_{2, 2}
  & a_{1, 1}w_{1, 1} + a_{1, 2}w_{1, 2} + a_{2, 1}w_{2, 1} + a_{2, 2}w_{2, 2}
  & a_{1, 2}w_{1, 1} + a_{1, 3}w_{1, 2} + a_{2, 2}w_{2, 1} + a_{2, 3}w_{2, 2}
  & a_{1, 3}w_{1, 1} + a_{1, 4}w_{1, 2} + a_{2, 3}w_{2, 1} + a_{2, 4}w_{2, 2}
  & a_{1, 4}w_{1, 1} + a_{2, 4}w_{2, 1} \\
    a_{2, 1}w_{1, 2} + a_{3, 1}w_{2, 2}
  & a_{2, 1}w_{1, 1} + a_{2, 2}w_{1, 2} + a_{3, 1}w_{2, 1} + a_{3, 2}w_{2, 2}
  & a_{2, 2}w_{1, 1} + a_{2, 3}w_{1, 2} + a_{3, 2}w_{2, 1} + a_{3, 3}w_{2, 2}
  & a_{2, 3}w_{1, 1} + a_{2, 4}w_{1, 2} + a_{3, 3}w_{2, 1} + a_{3, 4}w_{2, 2}
  & a_{2, 4}w_{1, 1} + a_{3, 4}w_{2, 1} \\
    a_{3, 1}w_{1, 2} + a_{4, 1}w_{2, 2}
  & a_{3, 1}w_{1, 1} + a_{3, 2}w_{1, 2} + a_{4, 1}w_{2, 1} + a_{4, 2}w_{2, 2}
  & a_{3, 2}w_{1, 1} + a_{3, 3}w_{1, 2} + a_{4, 2}w_{2, 1} + a_{4, 3}w_{2, 2}
  & a_{3, 3}w_{1, 1} + a_{3, 4}w_{1, 2} + a_{4, 3}w_{2, 1} + a_{4, 4}w_{2, 2}
  & a_{3, 4}w_{1, 1} + a_{4, 4}w_{2, 1} \\
    a_{4, 1}w_{1, 2}
  & a_{4, 1}w_{1, 1} + a_{4, 2}w_{1, 2}
  & a_{4, 2}w_{1, 1} + a_{4, 3}w_{1, 2}
  & a_{4, 3}w_{1, 1} + a_{4, 4}w_{1, 2}
  & a_{4, 4}w_{1, 1}
\end{array} \right)

なんだかイケる気がしてきませんか？
例えば

\left( \begin{array}[ccc]
  gg_{1, 1} & g_{1, 2} \\
  g_{2, 1} & g_{2, 2} \\
\end{array} \right)
= \left( \begin{array}[ccc]
  ww_{2, 2} & w_{2, 1} \\
  w_{1, 2} & w_{1, 1} \\
\end{array} \right)

なんてことをすると、

\left( \begin{array}[ccccc]
  ff_{1, 1}g_{1, 1}
& f_{1, 2}g_{1, 1} + f_{1, 1}g_{1, 2}
& f_{1, 3}g_{1, 1} + f_{1, 2}g_{1, 2}
& f_{1, 4}g_{1, 1} + f_{1, 3}g_{1, 2}
& f_{1, 4}g_{1, 2} \\
  f_{2, 1}g_{1, 1} + f_{1, 1}g_{2, 1}
& f_{2, 2}g_{1, 1} + f_{2, 1}g_{1, 2} + f_{1, 2}g_{2, 1} + f_{1, 1}g_{2, 2}
& f_{2, 3}g_{1, 1} + f_{2, 2}g_{1, 2} + f_{1, 3}g_{2, 1} + f_{1, 2}g_{2, 2}
& f_{2, 4}g_{1, 1} + f_{2, 3}g_{1, 2} + f_{1, 4}g_{2, 1} + f_{1, 3}g_{2, 2}
& f_{2, 4}g_{1, 2} + f_{1, 4}g_{2, 2} \\
  f_{3, 1}g_{1, 1} + f_{2, 1}g_{2, 1}
& f_{3, 2}g_{1, 1} + f_{3, 1}g_{1, 2} + f_{2, 2}g_{2, 1} + f_{2, 1}g_{2, 2}
& f_{3, 3}g_{1, 1} + f_{3, 2}g_{1, 2} + f_{2, 3}g_{2, 1} + f_{2, 2}g_{2, 2}
& f_{3, 4}g_{1, 1} + f_{3, 3}g_{1, 2} + f_{2, 4}g_{2, 1} + f_{2, 3}g_{2, 2}
& f_{3, 4}g_{1, 2} + f_{2, 4}g_{2, 2} \\
  f_{4, 1}g_{1, 1} + f_{3, 1}g_{2, 1}
& f_{4, 2}g_{1, 1} + f_{4, 1}g_{1, 2} + f_{3, 2}g_{2, 1} + f_{3, 1}g_{2, 2}
& f_{4, 3}g_{1, 1} + f_{4, 2}g_{1, 2} + f_{3, 3}g_{2, 1} + f_{3, 2}g_{2, 2}
& f_{4, 4}g_{1, 1} + f_{4, 3}g_{1, 2} + f_{3, 4}g_{2, 1} + f_{3, 3}g_{2, 2}
& f_{4, 4}g_{1, 2} + f_{3, 4}g_{2, 2} \\
  f_{4, 1}g_{2, 1}
& f_{4, 2}g_{2, 1} + f_{4, 1}g_{2, 2}
& f_{4, 3}g_{2, 1} + f_{4, 2}g_{2, 2}
& f_{4, 4}g_{2, 1} + f_{4, 3}g_{2, 2}
& f_{4, 4}g_{2, 2}
\end{array} \right) \\
= \left( \begin{array}[ccccc]
  ff_{1, 1}w_{2, 2}
& f_{1, 2}w_{2, 2} + f_{1, 1}w_{2, 1}
& f_{1, 3}w_{2, 2} + f_{1, 2}w_{2, 1}
& f_{1, 4}w_{2, 2} + f_{1, 3}w_{2, 1}
& f_{1, 4}w_{2, 1} \\
  f_{2, 1}w_{2, 2} + f_{1, 1}w_{1, 2}
& f_{2, 2}w_{2, 2} + f_{2, 1}w_{2, 1} + f_{1, 2}w_{1, 2} + f_{1, 1}w_{1, 1}
& f_{2, 3}w_{2, 2} + f_{2, 2}w_{2, 1} + f_{1, 3}w_{1, 2} + f_{1, 2}w_{1, 1}
& f_{2, 4}w_{2, 2} + f_{2, 3}w_{2, 1} + f_{1, 4}w_{1, 2} + f_{1, 3}w_{1, 1}
& f_{2, 4}w_{2, 1} + f_{1, 4}w_{1, 1} \\
  f_{3, 1}w_{2, 2} + f_{2, 1}w_{1, 2}
& f_{3, 2}w_{2, 2} + f_{3, 1}w_{2, 1} + f_{2, 2}w_{1, 2} + f_{2, 1}w_{1, 1}
& f_{3, 3}w_{2, 2} + f_{3, 2}w_{2, 1} + f_{2, 3}w_{1, 2} + f_{2, 2}w_{1, 1}
& f_{3, 4}w_{2, 2} + f_{3, 3}w_{2, 1} + f_{2, 4}w_{1, 2} + f_{2, 3}w_{1, 1}
& f_{3, 4}w_{2, 1} + f_{2, 4}w_{1, 1} \\
  f_{4, 1}w_{2, 2} + f_{3, 1}w_{1, 2}
& f_{4, 2}w_{2, 2} + f_{4, 1}w_{2, 1} + f_{3, 2}w_{1, 2} + f_{3, 1}w_{1, 1}
& f_{4, 3}w_{2, 2} + f_{4, 2}w_{2, 1} + f_{3, 3}w_{1, 2} + f_{3, 2}w_{1, 1}
& f_{4, 4}w_{2, 2} + f_{4, 3}w_{2, 1} + f_{3, 4}w_{1, 2} + f_{3, 3}w_{1, 1}
& f_{4, 4}w_{2, 1} + f_{3, 4}w_{1, 1} \\
  f_{4, 1}w_{1, 2}
& f_{4, 2}w_{1, 2} + f_{4, 1}w_{1, 1}
& f_{4, 3}w_{1, 2} + f_{4, 2}w_{1, 1}
& f_{4, 4}w_{1, 2} + f_{4, 3}w_{1, 1}
& f_{4, 4}w_{1, 1}
\end{array} \right) \\
\underbrace{=}_{足し算の順番入れ替え}
\left( \begin{array}[ccccc]
    ff_{1, 1}w_{2, 2}
  & f_{1, 1}w_{2, 1} + f_{1, 2}w_{2, 2}
  & f_{1, 2}w_{2, 1} + f_{1, 3}w_{2, 2}
  & f_{1, 3}w_{2, 1} + f_{1, 4}w_{2, 2} 
  & f_{1, 4}w_{2, 1} \\
    f_{1, 1}w_{1, 2} + f_{2, 1}w_{2, 2}
  & f_{1, 1}w_{1, 1} + f_{1, 2}w_{1, 2} + f_{2, 1}w_{2, 1} + f_{2, 2}w_{2, 2}
  & f_{1, 2}w_{1, 1} + f_{1, 3}w_{1, 2} + f_{2, 2}w_{2, 1} + f_{2, 3}w_{2, 2}
  & f_{1, 3}w_{1, 1} + f_{1, 4}w_{1, 2} + f_{2, 3}w_{2, 1} + f_{2, 4}w_{2, 2}
  & f_{1, 4}w_{1, 1} + f_{2, 4}w_{2, 1} \\
    f_{2, 1}w_{1, 2} + f_{3, 1}w_{2, 2}
  & f_{2, 1}w_{1, 1} + f_{2, 2}w_{1, 2} + f_{3, 1}w_{2, 1} + f_{3, 2}w_{2, 2}
  & f_{2, 2}w_{1, 1} + f_{2, 3}w_{1, 2} + f_{3, 2}w_{2, 1} + f_{3, 3}w_{2, 2}
  & f_{2, 3}w_{1, 1} + f_{2, 4}w_{1, 2} + f_{3, 3}w_{2, 1} + f_{3, 4}w_{2, 2}
  & f_{2, 4}w_{1, 1} + f_{3, 4}w_{2, 1} \\
    f_{3, 1}w_{1, 2} + f_{4, 1}w_{2, 2}
  & f_{3, 1}w_{1, 1} + f_{3, 2}w_{1, 2} + f_{4, 1}w_{2, 1} + f_{4, 2}w_{2, 2}
  & f_{3, 2}w_{1, 1} + f_{3, 3}w_{1, 2} + f_{4, 2}w_{2, 1} + f_{4, 3}w_{2, 2}
  & f_{3, 3}w_{1, 1} + f_{3, 4}w_{1, 2} + f_{4, 3}w_{2, 1} + f_{4, 4}w_{2, 2}
  & f_{3, 4}w_{1, 1} + f_{4, 4}w_{2, 1} \\
    f_{4, 1}w_{1, 2}
  & f_{4, 1}w_{1, 1} + f_{4, 2}w_{1, 2}
  & f_{4, 2}w_{1, 1} + f_{4, 3}w_{1, 2}
  & f_{4, 3}w_{1, 1} + f_{4, 4}w_{1, 2}
  & f_{4, 4}w_{1, 1}
\end{array} \right) \\
\Leftrightarrow
\left( \begin{array}[ccccc]
    aa_{1, 1}w_{2, 2}
  & a_{1, 1}w_{2, 1} + a_{1, 2}w_{2, 2}
  & a_{1, 2}w_{2, 1} + a_{1, 3}w_{2, 2}
  & a_{1, 3}w_{2, 1} + a_{1, 4}w_{2, 2} 
  & a_{1, 4}w_{2, 1} \\
    a_{1, 1}w_{1, 2} + a_{2, 1}w_{2, 2}
  & a_{1, 1}w_{1, 1} + a_{1, 2}w_{1, 2} + a_{2, 1}w_{2, 1} + a_{2, 2}w_{2, 2}
  & a_{1, 2}w_{1, 1} + a_{1, 3}w_{1, 2} + a_{2, 2}w_{2, 1} + a_{2, 3}w_{2, 2}
  & a_{1, 3}w_{1, 1} + a_{1, 4}w_{1, 2} + a_{2, 3}w_{2, 1} + a_{2, 4}w_{2, 2}
  & a_{1, 4}w_{1, 1} + a_{2, 4}w_{2, 1} \\
    a_{2, 1}w_{1, 2} + a_{3, 1}w_{2, 2}
  & a_{2, 1}w_{1, 1} + a_{2, 2}w_{1, 2} + a_{3, 1}w_{2, 1} + a_{3, 2}w_{2, 2}
  & a_{2, 2}w_{1, 1} + a_{2, 3}w_{1, 2} + a_{3, 2}w_{2, 1} + a_{3, 3}w_{2, 2}
  & a_{2, 3}w_{1, 1} + a_{2, 4}w_{1, 2} + a_{3, 3}w_{2, 1} + a_{3, 4}w_{2, 2}
  & a_{2, 4}w_{1, 1} + a_{3, 4}w_{2, 1} \\
    a_{3, 1}w_{1, 2} + a_{4, 1}w_{2, 2}
  & a_{3, 1}w_{1, 1} + a_{3, 2}w_{1, 2} + a_{4, 1}w_{2, 1} + a_{4, 2}w_{2, 2}
  & a_{3, 2}w_{1, 1} + a_{3, 3}w_{1, 2} + a_{4, 2}w_{2, 1} + a_{4, 3}w_{2, 2}
  & a_{3, 3}w_{1, 1} + a_{3, 4}w_{1, 2} + a_{4, 3}w_{2, 1} + a_{4, 4}w_{2, 2}
  & a_{3, 4}w_{1, 1} + a_{4, 4}w_{2, 1} \\
    a_{4, 1}w_{1, 2}
  & a_{4, 1}w_{1, 1} + a_{4, 2}w_{1, 2}
  & a_{4, 2}w_{1, 1} + a_{4, 3}w_{1, 2}
  & a_{4, 3}w_{1, 1} + a_{4, 4}w_{1, 2}
  & a_{4, 4}w_{1, 1}
\end{array} \right)

となり、同じになりました！これが意味することは相互相関と数学的な畳み込みとはうまくすれば同じ操作とすることが可能であるということです。この場合の「うまくする」は、離散であればインデックスの反転、連続の場合は原点対称ですね。

ということで、CNNのフィルタは反転した畳み込みフィルタを学習していると見なすことができ、研究者は泣かずに済むということですね笑

Cooley-Turkey FFTアルゴリズム

まずはそもそもの離散フーリエ変換の定義から確認してみます。簡単のため1次元の長さ$N$のベクトル$\boldsymbol{x}$を離散フーリエ変換で考えると

X_k = \mathcal{F}_{\boldsymbol{x}}(k) = \sum_{p=0}^{N-1}{x_p e^{-j\frac{2 \pi}{N}kp}} = \sum_{p=0}^{N-1}{x_p W_N^{kp}} \quad k = 0, 1, \ldots N-1 \\
W_N^{kp} = e^{-j\frac{2 \pi}{N}kp}

となります。ここで虚数記号を$j$としています。また$W_N = e^{-j\frac{2 \pi}{N}}$は回転因子と呼ばれています。理由は後述します。
この計算量は$\mathcal{O}(N^2)$ですが、この計算は$N$が偶数であると仮定すると高速化することができます。そのアルゴリズムはFFT: Fast Fourier Transformation: 高速フーリエ変換と呼ばれており、次のように表すことができます。

\begin{align}
  X_{2k} = \mathcal{F}_{\boldsymbol{x}}(2k) &= \sum_{p=0}^{N-1}{x_p W_N^{2kp}} & \\
  &= \sum_{p=0}^{N-1}{x_p W_{N/2}^{kp}} & (\because W_N^{2kp} = e^{-j\frac{2 \pi}{N}2kp} = e^{-j\frac{2 \pi}{N/2}kp} = W_{N/2}^{kp}) \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N/2}^{kp}} + \sum_{p=N/2}^{N-1}{x_p W_{N/2}^{kp}} & (\because 前半部分と後半部分に分け、W_{N/2}^{kp}の要素数\frac{N}{2}に合わせる) \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N/2}^{kp}} + \sum_{p=0}^{N/2-1}{x_{p+N/2} W_{N/2}^{k(p+N/2)}} & (\because 後半の和をp=0スタートにシフト) \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N/2}^{kp}} + \sum_{p=0}^{N/2-1}{x_{p+N/2} W_{N/2}^{kp}} & (\because W_{N/2}^{k(N/2)} = e^{-j\frac{2 \pi}{N/2}k(N/2)} = e^{-j2k \pi} = 1) \\
  &= \sum_{p=0}^{N/2-1}{(x_p + x_{p+N/2}) W_{N/2}^{kp}} \quad k = 0, 1, \ldots, \cfrac{N}{2} & \\

  X_{2k+1} = \mathcal{F}_{\boldsymbol{x}}(2k+1) &= \sum_{p=0}^{N-1}{x_p W_N^{(2k+1)p}} & \\
  &= \sum_{p=0}^{N-1}{x_p W_{N}^{p}W_{N/2}^{kp}} & \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N}^{p}W_{N/2}^{kp}} + \sum_{p=N/2}^{N-1}{x_p W_{N}^{p}W_{N/2}^{kp}} & \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N}^{p}W_{N/2}^{kp}} + \sum_{p=0}^{N/2-1}{x_{p+N/2} W_{N}^{p+N/2}W_{N/2}^{k(p+N/2)}} & \\
  &= \sum_{p=0}^{N/2-1}{x_p W_{N}^{p}W_{N/2}^{kp}} - \sum_{p=0}^{N/2-1}{x_{p+N/2} W_{N}^{p}W_{N/2}^{kp}} & \\
  &= \sum_{p=0}^{N/2-1}{(x_p - x_{p+N/2}) W_{N}^{p} W_{N/2}^{kp}} \quad k = 0, 1, \ldots, \cfrac{N}{2}-1 &
\end{align}

$W$は定義から回転角が時計回りに$\frac{2\pi}{N}$である単位円周上の点を表すことになるため、回転因子と呼ばれています。

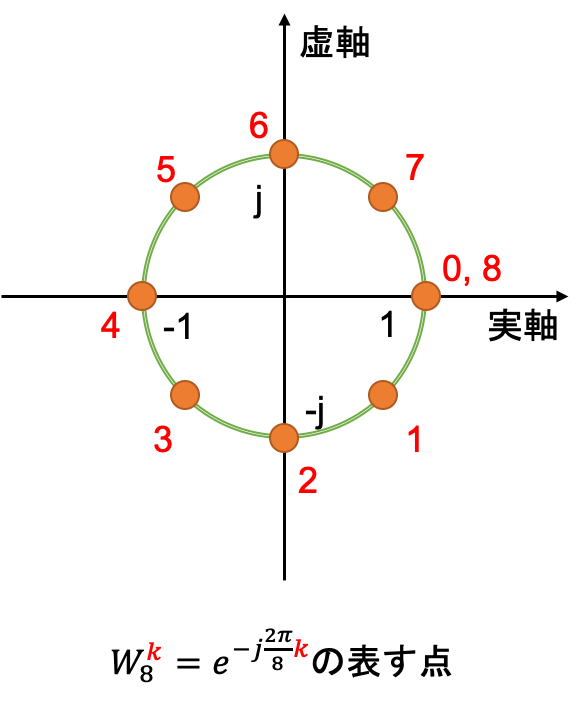
このため、以下のような関係式が成立します。

W_{2n}^{kn} = e^{-j\frac{2 \pi}{2n}kn} = e^{-j k \pi} = (-1)^k

この関係式は要するに回転角$k\pi$の時の値ですね。先のFFTの式変形にこの式を随所で用いています。

ナニコレ?という人へ

複素数に馴染みのない方には何をやっているのか分からないかもしれませんので、数学史上最も美しいと言われるオイラーの公式を紹介しておきます。さらにその前にテイラー展開も必要なのですが...その辺りは掘り出すと無限に話が膨らむので割愛します。

e^{jx} = \cos x + j \sin x

これがオイラーの公式です。これに$x=\pi$を代入して得られる

e^{j \pi} = \cos \pi + j \sin \pi \Leftrightarrow e^{j \pi} = -1 + j0 \\
\therefore e^{j \pi} + 1 = 0

は数学史上最も美しい式とよく評されています。その辺りの感性は残念ながらぼくにはあまりよくわかりませんが...まあすごいということ自体はわかります。とにかく、このオイラーの公式に$x=-k\pi$を代入すると

\begin{align}
  e^{j(-k \pi)} &= \cos (-k \pi) + j \sin (-k \pi) \\
  &= (-1)^k \\
\end{align}

となり、先ほどの関係式が得られます。

このFFTアルゴリズムにより計算量は半分になります。そしてこの操作を拡張したのがCooley-TurkeyのFFTアルゴリズムです。
Cooley_TurkeyのFFTアルゴリズムでは、ベクトルの長さ$N$を2の累乗であると仮定し、FFTを繰り返し適応することでさらなる高速化を図るものとなります。
分割を繰り返してベクトル長が$1$になるとそのフーリエ変換値を求めることで全てのフーリエ変換値が求まることになります。

具体的に計算してみる

**※間違ってたら教えてください！** 具体的に計算して確かめてみましょう。まずはFFTから確認します。入力を$\boldsymbol{x} = (x_0, x_1, \ldots, x_7)$の長さ$N=8$のベクトルであるとします。これのフーリエ変換ベクトルを$\boldsymbol{X} = (X_0, X_1, \ldots, X_7)$とすると、まずは定義通りに

\begin{align}
  \boldsymbol{X}^\top &= \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{7}{x_p W_8^{0}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{2p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{3p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{4p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{5p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{6p}} \\
    \displaystyle\sum_{p=0}^{7}{x_p W_8^{7p}} \\
  \end{array}\right)
  = \left( \begin{array}[c]
    xx_0W_8^0 + x_1W_8^0 + x_2W_8^0 + x_3W_8^0 + x_4W_8^0 + x_5W_8^0 + x_6W_8^0 + x_7W_8^0 \\
    x_0W_8^0 + x_1W_8^1 + x_2W_8^2 + x_3W_8^3 + x_4W_8^4 + x_5W_8^5 + x_6W_8^6 + x_7W_8^7 \\
    x_0W_8^0 + x_1W_8^2 + x_2W_8^4 + x_3W_8^6 + x_4W_8^8 + x_5W_8^{10} + x_6W_8^{12} + x_7W_8^{14} \\
    x_0W_8^0 + x_1W_8^3 + x_2W_8^6 + x_3W_8^9 + x_4W_8^{12} + x_5W_8^{15} + x_6W_8^{18} + x_7W_8^{21} \\
    x_0W_8^0 + x_1W_8^4 + x_2W_8^8 + x_3W_8^{12} + x_4W_8^{16} + x_5W_8^{20} + x_6W_8^{24} + x_7W_8^{28} \\
    x_0W_8^0 + x_1W_8^5 + x_2W_8^{10} + x_3W_8^{15} + x_4W_8^{20} + x_5W_8^{25} + x_6W_8^{30} + x_7W_8^{35} \\
    x_0W_8^0 + x_1W_8^6 + x_2W_8^{12} + x_3W_8^{18} + x_4W_8^{24} + x_5W_8^{30} + x_6W_8^{36} + x_7W_8^{42} \\
    x_0W_8^0 + x_1W_8^7 + x_2W_8^{14} + x_3W_8^{21} + x_4W_8^{28} + x_5W_8^{35} + x_6W_8^{42} + x_7W_8^{49} \\
  \end{array}\right) \\
  &= \left( \begin{array}[cccccccc]
    WW_8^0 & W_8^0 & W_8^0 & W_8^0 & W_8^0 & W_8^0 & W_8^0 & W_8^0 \\
    W_8^0 & W_8^1 & W_8^2 & W_8^3 & W_8^4 & W_8^5 & W_8^6 & W_8^7 \\
    W_8^0 & W_8^2 & W_8^4 & W_8^6 & W_8^8 & W_8^{10} & W_8^{12} & W_8^{14} \\
    W_8^0 & W_8^3 & W_8^6 & W_8^9 & W_8^{12} & W_8^{15} & W_8^{18} & W_8^{21} \\
    W_8^0 & W_8^4 & W_8^8 & W_8^{12} & W_8^{16} & W_8^{20} & W_8^{24} & W_8^{28} \\
    W_8^0 & W_8^5 & W_8^{10} & W_8^{15} & W_8^{20} & W_8^{25} & W_8^{30} & W_8^{35} \\
    W_8^0 & W_8^6 & W_8^{12} & W_8^{18} & W_8^{24} & W_8^{30} & W_8^{36} & W_8^{42} \\
    W_8^0 & W_8^7 & W_8^{14} & W_8^{21} & W_8^{28} & W_8^{35} & W_8^{42} & W_8^{49} \\
  \end{array}\right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7 \\
  \end{array}\right) \\
  &= \left( \begin{array}[cccccccc]
    11 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
    1 & e^{-j\frac{\pi}{4}} & -j & e^{-j\frac{3\pi}{4}} & -1 & e^{-j\frac{5\pi}{4}} & j & e^{-j\frac{7\pi}{4}} \\
    1 & -j & -1 & j & 1 & -j & -1 & j \\
    1 & e^{-j\frac{3\pi}{4}} & j & e^{-j\frac{\pi}{4}} & -1 & e^{-j\frac{7\pi}{4}} & -j & e^{-j\frac{5\pi}{4}} \\
    1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\
    1 & e^{-j\frac{5\pi}{4}} & -j & e^{-j\frac{7\pi}{4}} & -1 & e^{-j\frac{\pi}{4}} & j & e^{-j\frac{3\pi}{4}} \\
    1 & j & -1 & -j & 1 & j & -1 & -j \\
    1 & e^{-j\frac{7\pi}{4}} & j & e^{-j\frac{5\pi}{4}} & -1 & e^{-j\frac{3\pi}{4}} & -j & e^{-j\frac{\pi}{4}} \\
  \end{array}\right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7 \\
  \end{array}\right)
\end{align}

と書くことができます。これと一致するか確認しながら計算していきます。

\begin{align}
  X_{2k} &= \sum_{p=0}^{3}{(x_p + x_{p+4}) W_{4}^{kp}} \\
  X_{2k+1} &= \sum_{p=0}^{3}{(x_p - x_{p+4})W_{8}^{p} W_{4}^{kp}}
\end{align}

ですから

\begin{align}
  X^{(0)} &= (X_0, X_2, X_4, X_6) \\
  X^{(1)} &= (X_1, X_3, X_5, X_7)
\end{align}

として

\begin{align}
  X^{(0)\top} &= \left( \begin{array}[c]
    XX_0 \\
    X_2 \\
    X_4 \\
    X_6
  \end{array} \right) = \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{3}{(x_p + x_{p+4}) W_4^{0}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p + x_{p+4}) W_4^{p}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p + x_{p+4}) W_4^{2p}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p + x_{p+4}) W_4^{3p}}
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    ((x_0 + x_4) W_4^0 + (x_1 + x_5) W_4^0 + (x_2 + x_6) W_4^0 + (x_3 + x_7) W_4^0 \\
    (x_0 + x_4) W_4^0 + (x_1 + x_5) W_4^1 + (x_2 + x_6) W_4^2 + (x_3 + x_7) W_4^3 \\
    (x_0 + x_4) W_4^0 + (x_1 + x_5) W_4^2 + (x_2 + x_6) W_4^4 + (x_3 + x_7) W_4^6 \\
    (x_0 + x_4) W_4^0 + (x_1 + x_5) W_4^3 + (x_2 + x_6) W_4^6 + (x_3 + x_7) W_4^9 \\
  \end{array} \right) & \\
　&= \left( \begin{array}[c]
    xx_0 W_4^0 + x_1 W_4^0 + x_2 W_4^0 + x_3 W_4^0 + x_4 W_4^0 + x_5 W_4^0 + x_6 W_4^0 + x_7 W_4^0 \\
    x_0 W_4^0 + x_1 W_4^1 + x_2 W_4^2 + x_3 W_4^3 + x_4 W_4^0 + x_5 W_4^1 + x_6 W_4^2 + x_7 W_4^3 \\
    x_0 W_4^0 + x_1 W_4^2 + x_2 W_4^4 + x_3 W_4^6 + x_4 W_4^0 + x_5 W_4^2 + x_6 W_4^4 + x_7 W_4^6 \\
    x_0 W_4^0 + x_1 W_4^3 + x_2 W_4^6 + x_3 W_4^9 + x_4 W_4^0 + x_5 W_4^3 + x_6 W_4^6 + x_7 W_4^9 \\
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    WW_4^0 & W_4^0 & W_4^0 & W_4^0 & W_4^0 & W_4^0 & W_4^0 & W_4^0 \\
    W_4^0 & W_4^1 & W_4^2 & W_4^3 & W_4^0 & W_4^1 & W_4^2 & W_4^3 \\
    W_4^0 & W_4^2 & W_4^4 & W_4^6 & W_4^0 & W_4^2 & W_4^4 & W_4^6 \\
    W_4^0 & W_4^3 & W_4^6 & W_4^9 & W_4^0 & W_4^3 & W_4^6 & W_4^9 \\
  \end{array} \right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    11 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
    1 & -j & -1 & j & 1 & -j & -1　& j \\
    1 & -1 & 1 & -1 & 1 & -1 & 1 & -1 \\
    1 & j & -1 & -j & 1 & j & -1 & j \\
  \end{array} \right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\

  X^{(1)\top} &= \left( \begin{array}[c]
    XX_1 \\
    X_3 \\
    X_5 \\
    X_7
  \end{array} \right) = \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{3}{(x_p - x_{p+4})W_8^{p} W_4^{0}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p - x_{p+4})W_8^{p} W_4^{p}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p - x_{p+4})W_8^{p} W_4^{2p}} \\
    \displaystyle\sum_{p=0}^{3}{(x_p - x_{p+4})W_8^{p} W_4^{3p}}
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    ((x_0 - x_4)W_8^{0} W_4^0 + (x_1 - x_5)W_8^1 W_4^0 + (x_2 - x_6)W_8^2 W_4^0 + (x_3 - x_7)W_8^3 W_4^0 \\
    (x_0 - x_4)W_8^0 W_4^0 + (x_1 - x_5)W_8^1 W_4^1 + (x_2 - x_6)W_8^2 W_4^2 + (x_3 - x_7)W_8^3 W_4^3 \\
    (x_0 - x_4)W_8^0 W_4^0 + (x_1 - x_5)W_8^1 W_4^2 + (x_2 - x_6)W_8^2 W_4^4 + (x_3 - x_7)W_8^3 W_4^6 \\
    (x_0 - x_4)W_8^0 W_4^0 + (x_1 - x_5)W_8^1 W_4^3 + (x_2 - x_6)W_8^2 W_4^6 + (x_3 - x_7)W_8^3 W_4^9 \\
  \end{array} \right) & \\
　&= \left( \begin{array}[c]
    xx_0 W_8^0 W_4^0 + x_1 W_8^1 W_4^0 + x_2 W_8^2 W_4^0 + x_3 W_8^3 W_4^0 - x_4 W_8^0 W_4^0 - x_5 W_8^1 W_4^0 - x_6 W_8^2 W_4^0 - x_7 W_8^3 W_4^0 \\
    x_0 W_8^0 W_4^0 + x_1 W_8^1 W_4^2 + x_2 W_8^2 W_4^4 + x_3 W_8^3 W_4^6 - x_4 W_8^0 W_4^0 - x_5 W_8^1 W_4^2 - x_6 W_8^2 W_4^4 - x_7 W_8^3 W_4^6 \\
    x_0 W_8^0 W_4^0 + x_1 W_8^1 W_4^3 + x_2 W_8^2 W_4^6 + x_3 W_8^3 W_4^9 - x_4 W_8^0 W_4^0 - x_5 W_8^1 W_4^3 - x_6 W_8^2 W_4^6 - x_7 W_8^3 W_4^9 \\
    x_0 W_8^0 W_4^0 + x_1 W_8^1 W_4^4 + x_2 W_8^2 W_4^8 + x_3 W_8^3 W_4^{12} - x_4 W_8^0 W_4^0 - x_5 W_8^1 W_4^4 - x_6 W_8^2 W_4^8 - x_7 W_8^3 W_4^{12}
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    WW_8^0 & W_8^1 & W_8^2 & W_8^3 & -W_8^0 & -W_8^1 & -W_8^2 & -W_8^3 \\
    W_8^0 & W_8^5 & W_8^{10} & W_8^{15} & -W_8^0 & -W_8^5 & -W_8^{10} & -W_8^{15} \\
    W_8^0 & W_8^7 & W_8^{14} & W_8^{21} & -W_8^0 & -W_8^7 & -W_8^{14} & -W_8^{21} \\
    W_8^0 & W_8^9 & W_8^{18} & W_8^{27} & -W_8^0 & -W_8^9 & -W_8^{18} & -W_8^{27} \\
  \end{array} \right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & (\because W_8^c W_4^d = W_8^{c+2d}) \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{\pi}{4}} & -j & e^{-j\frac{3\pi}{4}} & -1 & e^{-j\frac{5\pi}{4}} & j & e^{-j\frac{7\pi}{4}} \\
    1 & e^{-j\frac{3\pi}{4}} & j & e^{-j\frac{\pi}{4}} & -1 & e^{-j\frac{7\pi}{4}} & -j & e^{-j\frac{5\pi}{4}} \\
    1 & e^{-j\frac{5\pi}{4}} & -j & e^{-j\frac{7\pi}{4}} & -1 & e^{-j\frac{\pi}{4}} & j & e^{-j\frac{3\pi}{4}} \\
    1 & e^{-j\frac{7\pi}{4}} & j & e^{-j\frac{5\pi}{4}} & -1 & e^{-j\frac{3\pi}{4}} & -j & e^{-j\frac{\pi}{4}} \\
  \end{array} \right)
  \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & (\because -1 = W_8^4)
\end{align}

きっちり偶数列と奇数列の値がそれぞれ計算できていますね！それではさらにCooley-Turekeyアルゴリズムで試していきましょう。まず下準備として

\begin{align}
  \boldsymbol{x}^{(0)} &= (x_0 + x_4, x_1 + x_5, x_2 + x_6, x_3 + x_7) \\ 
  \boldsymbol{x}^{(1)} &= \left((x_0 - x_4)W_8^0, (x_1 - x_5)W_8^1, (x_2 - x_6)W_8^2, (x_3 - x_7)W_8^3 \right)
\end{align}

とおきます。この場合

\left\{ \begin{array}[c]
  b\boldsymbol{X}^{(0)} = \mathcal{F}_{\boldsymbol{x}^{(0)}}(k) \\
  \boldsymbol{X}^{(1)} = \mathcal{F}_{\boldsymbol{x}^{(1)}}(k)
\end{array} \right.
\quad k = 0, 1, \ldots, 3

とすることができますね。このそれぞれに対してFFTを行うと

\begin{align}
  \boldsymbol{X}_{2k}^{(0)} &= \mathcal{F}_{\boldsymbol{x}^{(0)}}(2k) \\
  &= \sum_{p=0}^{1}{\left(x_p^{(0)} + x_{p+2}^{(0)} \right) W_{2}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(0)} &= \mathcal{F}_{\boldsymbol{x}^{(0)}}(2k+1) \\
  &= \sum_{p=0}^{1}{\left(x_p^{(0)} - x_{p+2}^{(0)} \right)W_4^p W_{2}^{kp}} \\
　　\boldsymbol{X}_{2k}^{(1)} &= \mathcal{F}_{\boldsymbol{x}^{(1)}}(2k) \\
  &= \sum_{p=0}^{1}{\left(x_p^{(1)} + x_{p+2}^{(1)} \right) W_{2}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(1)} &= \mathcal{F}_{\boldsymbol{x}^{(1)}}(2k+1) \\
  &= \sum_{p=0}^{1}{\left(x_p^{(1)} - x_{p+2}^{(1)}\right)W_4^p W_{2}^{kp}}
\end{align}

となります。一応実際に書き下して正しいか確認しておきます。

\begin{align}
  \boldsymbol{X}_{2k}^{(0)} &= \left( \begin{array}[c]
    XX_{0}^{(0)} \\
    X_{2}^{(0)}
  \end{array} \right) = \left( \begin{array}[c]
    XX_0 \\
    X_4
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{1}{\left(x_p^{(0)} + x_{p+2}^{(0)} \right) W_2^0} \\
    \displaystyle\sum_{p=0}^{1}{\left(x_p^{(0)} + x_{p+2}^{(0)} \right) W_2^p}
  \end{array} \right) = \left( \begin{array}[c]
    (\left(x_0^{(0)} + x_2^{(0)} \right) W_2^0 + \left(x_1^{(0)} + x_3^{(0)} \right) W_2^0 \\
    \left(x_0^{(0)} + x_2^{(0)} \right) W_2^0 + \left(x_1^{(0)} + x_3^{(0)} \right) W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    (\{(x_0 + x_4) + (x_2 + x_6)\}W_2^0 + \{(x_1 + x_5) + (x_3 + x_7) \} W_2^0 \\
    \{(x_0 + x_4) + (x_2 + x_6)\}W_2^0 + \{(x_1 + x_5) + (x_3 + x_7) \} W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    WW_2^0 & W_2^0 & W_2^0 & W_2^0 & W_2^0 & W_2^0 & W_2^0 & W_2^0 \\
    W_2^0 & W_2^1 & W_2^0 & W_2^1 & W_2^0 & W_2^1 & W_2^0 & W_2^1
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) && \\
  &= \left( \begin{array}[cccccccc]
    11 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\
    1 & -1 & 1 & -1 & 1 & -1 & 1 & -1
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\

  \boldsymbol{X}_{2k+1}^{(0)} &= \left( \begin{array}[c]
    XX_{1}^{(0)} \\
    X_{3}^{(0)}
  \end{array} \right) = \left( \begin{array}[c]
    XX_2 \\
    X_6
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{1}{\left(x_p^{(0)} - x_{p+2}^{(0)} \right)W_4^p W_2^0} \\
    \displaystyle\sum_{p=0}^{1}{\left(x_p^{(0)} - x_{p+2}^{(0)} \right)W_4^p W_2^p}
  \end{array} \right) = \left( \begin{array}[c]
    (\left(x_0^{(0)} - x_2^{(0)} \right)W_4^0 W_2^0 + \left(x_1^{(0)} - x_3^{(0)} \right)W_4^1 W_2^0 \\
    \left(x_0^{(0)} - x_2^{(0)} \right)W_4^0 W_2^0 + \left(x_1^{(0)} - x_3^{(0)} \right)W_4^1 W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    (\{(x_0 + x_4) - (x_2 + x_6)\}W_4^0 W_2^0 + \{(x_1 + x_5) - (x_3 + x_7)\}W_4^1 W_2^0 \\
    \{(x_0 + x_4) - (x_2 + x_6)\}W_4^0 W_2^0 + \{(x_1 + x_5) - (x_3 + x_7)\}W_4^1 W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    WW_4^0 & W_4^1 & -W_4^0 & -W_4^1 & W_4^0 & W_4^1 & -W_4^0 & -W_4^1 \\
    W_4^0 & W_4^5 & -W_4^0 & -W_4^5 & W_4^0 & W_4^5 & -W_4^0 & -W_4^5
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    11 & -j & -1 & j & 1 & -j & -1 & j \\
    1 & j & -1 & -j & 1 & j & -1 & -j
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & (\because W_4^c W_2^d = W_4^{c+2d}, -1 = W_4^2) \\

  \boldsymbol{X}_{2k}^{(1)} &= \left( \begin{array}[c]
    XX_{0}^{(1)} \\
    X_{2}^{(1)}
  \end{array} \right) = \left( \begin{array}[c]
    XX_1 \\
    X_5
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{1}{\left(x_p^{(1)} + x_{p+2}^{(1)} \right) W_2^0} \\
    \displaystyle\sum_{p=0}^{1}{\left(x_p^{(1)} + x_{p+2}^{(1)} \right) W_2^p}
  \end{array} \right) = \left( \begin{array}[c]
    (\left(x_0^{(1)} + x_2^{(1)} \right) W_2^0 + \left(x_1^{(1)} + x_3^{(1)} \right) W_2^0 \\
    \left(x_0^{(1)} + x_2^{(1)} \right) W_2^0 + \left(x_1^{(1)} + x_3^{(1)} \right) W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    (\left\{(x_0 - x_4)W_8^0 + (x_2 - x_6)W_8^2 \right\}W_2^0 + \left\{(x_1 - x_5)W_8^1 + (x_3 - x_7)W_8^3 \right\}W_2^0 \\
    \left\{(x_0 - x_4)W_8^0 + (x_2 - x_6)W_8^2 \right\}W_2^0 + \left\{(x_1 - x_5)W_8^1 + (x_3 - x_7)W_8^3 \right\}W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    WW_8^0 & W_8^1 & W_8^2 & W_8^3 & -W_8^0 & -W_8^1 & -W_8^2 & -W_8^3 \\
    W_8^0 & W_8^5 & W_8^2 & W_8^7 & -W_8^0 & -W_8^5 & -W_8^2 & -W_8^7
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{\pi}{4}} & -j & e^{-j\frac{3\pi}{4}} & -1 & e^{-j\frac{5\pi}{4}} & j & e^{-j\frac{7\pi}{4}} \\
    1 & e^{-j\frac{5\pi}{4}} & -j & e^{-j\frac{7\pi}{4}} & -1 & e^{-j\frac{\pi}{4}} & j & e^{-j\frac{3\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\

  \boldsymbol{X}_{2k+1}^{(1)} &= \left( \begin{array}[c]
    XX_{1}^{(1)} \\
    X_{3}^{(1)}
  \end{array} \right) = \left( \begin{array}[c]
    XX_3 \\
    X_7
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    d\displaystyle\sum_{p=0}^{1}{\left(x_p^{(1)} - x_{p+2}^{(1)} \right)W_4^p W_2^0} \\
    \displaystyle\sum_{p=0}^{1}{\left(x_p^{(1)} - x_{p+2}^{(1)} \right)W_4^p W_2^p}
  \end{array} \right) = \left( \begin{array}[c]
    (\left(x_0^{(1)} - x_2^{(1)} \right)W_4^0 W_2^0 + \left(x_1^{(1)} - x_3^{(1)} \right)W_4^1 W_2^0 \\
    \left(x_0^{(1)} - x_2^{(1)} \right)W_4^0 W_2^0 + \left(x_1^{(1)} - x_3^{(1)} \right)W_4^1 W_2^1
  \end{array} \right) & \\
  &= \left( \begin{array}[c]
    (\left\{(x_0 - x_4)W_8^0 - (x_2 - x_6)W_8^2 \right\}W_4^0 W_2^0 + \left\{(x_1 - x_5)W_8^1 - (x_3 - x_7)W_8^3 \right\}W_4^1 W_2^0 \\
    \left\{(x_0 - x_4)W_8^0 - (x_2 - x_6)W_8^2 \right\}W_4^0 W_2^0 + \left\{(x_1 - x_5)W_8^1 - (x_3 - x_7)W_8^3 \right\}W_4^1 W_2^1
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    WW_8^0 & W_8^3 & -W_8^2 & -W_8^5 & -W_8^0 & -W_8^3 & W_8^2 & W_8^5 \\
    W_8^0 & W_8^7 & -W_8^2 & -W_8^9 & -W_8^0 & -W_8^7 & W_8^2 & W_8^9
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{3\pi}{4}} & j & e^{-j\frac{\pi}{4}} & -1 & e^{-j\frac{7\pi}{4}} & -j & e^{-j\frac{5\pi}{4}} \\
    1 & e^{-j\frac{7\pi}{4}} & j & e^{-j\frac{5\pi}{4}} & -1 & e^{-j\frac{3\pi}{4}} & -j & e^{-j\frac{\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) & \left(\because W_8^c W_4^d W_2^e = W_8^{c+2d+4e}, -1 = W_8^4 \right)
\end{align}

正しく計算できていることがわかりますね(遠い目)。ではもう一回FFTを適用しましょう。

\begin{align}
  \boldsymbol{x}^{(00)} &= \left(x_0^{(0)} + x_2^{(0)}, x_1^{(0)} + x_3^{(0)} \right) = \big((x_0 + x_4) + (x_2 + x_6), (x_1 + x_5) + (x_3 + x_7) \big) \\
  \boldsymbol{x}^{(01)} &= \left( \left(x_0^{(0)} - x_2^{(0)} \right)W_4^0, \left(x_1^{(0)} - x_3^{(0)} \right)W_4^1 \right) = \left(\{(x_0 + x_4) - (x_2 + x_6)\}W_4^0, \{(x_1 + x_5) - (x_3 + x_7)\}W_4^1 \right) \\
  \boldsymbol{x}^{(10)} &= \left(x_0^{(1)} + x_2^{(1)}, x_1^{(1)} + x_3^{(1)} \right) = \left((x_0 - x_4)W_8^0 + (x_2 - x_6)W_8^2, (x_1 - x_5)W_8^1 + (x_3 - x_7)W_8^3 \right) \\
  \boldsymbol{x}^{(11)} &= \left( \left(x_0^{(0)} - x_2^{(0)} \right)W_4^0, \left(x_1^{(0)} - x_3^{(0)} \right)W_4^1 \right) = \left( \left\{(x_0 - x_4)W_8^0 - (x_2 - x_6)W_8^2 \right\}W_4^0, \left\{(x_1 - x_5)W_8^1 - (x_3 - x_7)W_8^3 \right\}W_4^1 \right)
\end{align}

とすると

\left\{ \begin{array}[c]
  b\boldsymbol{X}^{(00)} = \mathcal{F}_{\boldsymbol{x}^{(00)}}(k) \\
  \boldsymbol{X}^{(01)} = \mathcal{F}_{\boldsymbol{x}^{(01)}}(k) \\
  \boldsymbol{X}^{(10)} = \mathcal{F}_{\boldsymbol{x}^{(10)}}(k) \\
  \boldsymbol{X}^{(11)} = \mathcal{F}_{\boldsymbol{x}^{(11)}}(k)
\end{array} \right.
\quad k = 0, 1

ですので

\begin{align}
  \boldsymbol{X}_{2k}^{(00)} &= \mathcal{F}_{\boldsymbol{x}^{(00)}}(2k) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(00)} + x_{p+1}^{(00)}\right) W_{1}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(00)} &= \mathcal{F}_{\boldsymbol{x}^{(00)}}(2k+1) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(00)} - x_{p+1}^{(00)}\right)W_2^{p} W_{1}^{kp}} \\
  \boldsymbol{X}_{2k}^{(01)} &= \mathcal{F}_{\boldsymbol{x}^{(01)}}(2k) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(01)} + x_{p+1}^{(01)}\right) W_{1}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(01)} &= \mathcal{F}_{\boldsymbol{x}^{(01)}}(2k+1) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(01)} - x_{p+1}^{(01)}\right)W_2^{p} W_{1}^{kp}} \\
  \boldsymbol{X}_{2k}^{(10)} &= \mathcal{F}_{\boldsymbol{x}^{(10)}}(2k) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(10)} + x_{p+1}^{(10)}\right) W_{1}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(10)} &= \mathcal{F}_{\boldsymbol{x}^{(10)}}(2k+1) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(10)} - x_{p+1}^{(10)}\right)W_2^{p} W_{1}^{kp}} \\
  \boldsymbol{X}_{2k}^{(11)} &= \mathcal{F}_{\boldsymbol{x}^{(11)}}(2k) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(11)} + x_{p+1}^{(11)}\right) W_{1}^{kp}} \\
  \boldsymbol{X}_{2k+1}^{(11)} &= \mathcal{F}_{\boldsymbol{x}^{(11)}}(2k+1) \\
  &= \sum_{p=0}^{0}{\left(x_p^{(11)} - x_{p+1}^{(11)}\right)W_2^{p} W_{1}^{kp}} \\
\end{align}

こ、ここまできたら気合でやってやる...!

\begin{align}
  \boldsymbol{X}_{2k}^{(00)} &= X_0 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(00)} + x_{p+1}^{(00)}\right) W_{1}^{0}} = \left(x_0^{(00)} + x_{1}^{(00)}\right) W_{1}^{0} \\
  &= \left(((x_0 + x_4) + (x_2 + x_6)) + ((x_1 + x_5) + (x_3 + x_7))\right) W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{1}^{0} & W_{1}^{0} & W_{1}^{0} & W_{1}^{0} & W_{1}^{0} & W_{1}^{0} & W_{1}^{0} & W_{1}^{0}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & 1 & 1 & 1 & 1 & 1 & 1 & 1
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k+1}^{(00)} &= X_4 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(00)} - x_{p+1}^{(00)}\right)W_2^{p} W_{1}^{kp}} = \left(x_0^{(00)} - x_{1}^{(00)}\right)W_2^0 W_{1}^{0} \\
  &= \left(((x_0 + x_4) + (x_2 + x_6)) - ((x_1 + x_5) + (x_3 + x_7))\right) W_2^0 W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{2}^{0} & -W_{2}^{0} & W_{2}^{0} & -W_{2}^{0} & W_{2}^{0} & -W_{2}^{0} & W_{2}^{0} & -W_{2}^{0}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & -1 & 1 & -1 & 1 & -1 & 1 & -1
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k}^{(01)} &= X_2 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(01)} + x_{p+1}^{(01)}\right) W_{1}^{kp}} = \left(x_0^{(01)} + x_{1}^{(01)}\right) W_{1}^{0} \\
  &= \left(\{(x_0 + x_4) - (x_2 + x_6)\}W_4^0 + \{(x_1 + x_5) - (x_3 + x_7)\}W_4^1 \right) W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{4}^{0} & W_{4}^{1} & -W_{4}^{0} & -W_{4}^{1} & W_{4}^{0} & W_{4}^{1} & -W_{4}^{0} & -W_{4}^{1}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & -j & -1 & j & 1 & -j & -1 & j \\
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

\boldsymbol{X}_{2k+1}^{(01)} &= X_6 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(01)} - x_{p+1}^{(01)}\right)W_2^{p} W_{1}^{kp}} = \left(x_0^{(01)} - x_{1}^{(01)}\right)W_2^0 W_{1}^{0} \\
  &= \left(\{(x_0 + x_4) - (x_2 + x_6)\}W_4^0 - \{(x_1 + x_5) - (x_3 + x_7)\}W_4^1 \right) W_2^0 W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{4}^{0} & -W_{4}^{1} & -W_{4}^{0} & W_{4}^{1} & W_{4}^{0} &  -W_{4}^{1} & -W_{4}^{0} & W_{4}^{1}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & j & -1 & -j & 1 & j & -1 & -j
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k}^{(10)} &= X_1 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(10)} + x_{p+1}^{(10)}\right) W_{1}^{0}} = \left(x_0^{(10)} + x_{1}^{(10)}\right) W_{1}^{0} \\
  &= \left(((x_0 - x_4)W_8^0 + (x_2 - x_6)W_8^2) + ((x_1 - x_5)W_8^1 + (x_3 - x_7)W_8^3) \right) W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{8}^{0} & W_{8}^{1} & W_{8}^{2} & W_{8}^{3} & -W_{8}^{0} & -W_{8}^{1} & -W_{8}^{2} & -W_{8}^{3}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{\pi}{4}} & -j & e^{-j\frac{3\pi}{4}} & -1 & e^{-j\frac{5\pi}{4}} & j & e^{-j\frac{7\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k+1}^{(10)} &= X_5 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(10)} - x_{p+1}^{(10)}\right)W_2^{p} W_{1}^{kp}} = \left(x_0^{(10)} - x_{1}^{(10)}\right)W_2^0 W_{1}^{0} \\
  &= \left(\{(x_0 - x_4)W_8^0 + (x_2 - x_6)W_8^2\} - \{(x_1 - x_5)W_8^1 + (x_3 - x_7)W_8^3\}\right) W_2^0 W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{8}^{0} & -W_{8}^{1} & W_{8}^{2} & -W_{8}^{3} & -W_{8}^{0} & W_{8}^{1} & -W_{8}^{2} & W_{8}^{3}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{5\pi}{4}} & -j & e^{-j\frac{7\pi}{4}} & -1 & e^{-j\frac{\pi}{4}} & j & e^{-j\frac{3\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k}^{(11)} &= X_3 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(11)} + x_{p+1}^{(11)}\right) W_{1}^{0}} = \left(x_0^{(11)} + x_{1}^{(11)}\right) W_{1}^{0} \\
  &= \left(\{(x_0 - x_4)W_8^0 - (x_2 - x_6)W_8^2\}W_4^0 + \{(x_1 - x_5)W_8^1 - (x_3 - x_7)W_8^3\}W_4^1 \right) W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{8}^{0} & W_{8}^{3} & -W_{8}^{2} & -W_{8}^{5} & -W_{8}^{0} & -W_{8}^{3} & W_{8}^{2} & W_{8}^{5}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{3\pi}{4}} & j & e^{-j\frac{\pi}{4}} & -1 & e^{-j\frac{7\pi}{4}} & -j & e^{-j\frac{5\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\

  \boldsymbol{X}_{2k+1}^{(11)} &= X_7 \\
  &= \sum_{p=0}^{0}{\left(x_p^{(11)} - x_{p+1}^{(11)}\right)W_2^{p} W_{1}^{kp}} = \left(x_0^{(11)} - x_{1}^{(11)}\right)W_2^0 W_{1}^{0} \\
  &= \left(\{(x_0 - x_4)W_8^0 - (x_2 - x_6)W_8^2\}W_4^0 - \{(x_1 - x_5)W_8^1 - (x_3 - x_7)W_8^3\}W_4^1\right) W_2^0 W_{1}^{0} \\
  &= \left( \begin{array}[cccccccc]
    WW_{8}^{0} & -W_{8}^{3} & -W_{8}^{2} & W_{8}^{5} & -W_{8}^{0} & W_{8}^{3} & W_{8}^{2} -& W_{8}^{5}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right) \\
  &= \left( \begin{array}[cccccccc]
    11 & e^{-j\frac{7\pi}{4}} & j & e^{-j\frac{5\pi}{4}} & -1 & e^{-j\frac{3\pi}{4}} & -j & e^{-j\frac{\pi}{4}}
  \end{array} \right) \left( \begin{array}[c]
    xx_0 \\
    x_1 \\
    x_2 \\
    x_3 \\
    x_4 \\
    x_5 \\
    x_6 \\
    x_7
  \end{array} \right)
\end{align}

という感じですね！しっかり一致しています。
ここまでの書き下しによる計算の確認では$\boldsymbol{x}^{(0)}$などを展開して計算していますが、実際の実装ではそのようなことは行われないことに注意してください。
また、お気づきの方もいらっしゃるかもしれませんが、下記のようにビット反転並び替えが発生しています。

X^{(000)} = X_{2k}^{(00)} = X_0 = X_{(000)_{(2)}} \quad
X^{(001)} = X_{2k+1}^{(00)} = X_4 = X_{(100)_{(2)}} \\
X^{(010)} = X_{2k}^{(01)} = X_2 = X_{(010)_{(2)}} \quad
X^{(011)} = X_{2k+1}^{(01)} = X_6 = X_{(110)_{(2)}} \\
X^{(100)} = X_{2k}^{(10)} = X_1 = X_{(001)_{(2)}} \quad
X^{(101)} = X_{2k+1}^{(10)} = X_5 = X_{(101)_{(2)}} \\
X^{(110)} = X_{2k}^{(11)} = X_3 = X_{(011)_{(2)}} \quad
X^{(111)} = X_{2k+1}^{(11)} = X_7 = X_{(111)_{(2)}}

分解の仕方を考えると当然といえば当然の順番の入れ替えが発生しています。このままだと効率が悪いので、実装の段階でうまくすることで正しい順序で計算できるようにすることができます。
詳しくは参考サイトをご覧ください。

これにより計算量は$\mathcal{O}(N \log_2 N)$まで削減されます。計算量の世界において対数オーダというのは非常に優秀なものであり、$N$の値が余程法外な値を取らなければ現実的な時間内に計算を終えることができるという保証になります。

とまあそんな具合で高速なフーリエ変換が可能となるわけです。ただ、時間計算量のオーダが$\mathcal{O}(N \log_2 N)$となる大変有効な計算手法ではありますが欠点がないわけでなく、仮定から空間計算量の観点では効率が悪くなります。なんせ2の累乗に揃える必要があります。通常はゼロパディングで行いますが、変換対象のサイズが大きくなればなるほど2の累乗から離れやすくなり、余分に無駄なゼロパディングをする必要が出てきます。
そのため、使用する場合はメモリの余裕などをきちんと考慮して時間/空間計算量のトレードオフを加味しましょう。

参考

おわりに

付録の方が本編の10倍は時間掛かった...誰の役に立つのやら...
今後FCNN関連の論文をこんな感じでまとめつつ情報収集していずれ実装していきたいなぁと思っています。
何か情報をお持ちの方はぜひ教えてください！

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up