陰関数を用いてベジェ曲線の交点を求める手法を実装してみました。
方式
方式は前回の通りです。ただし、フーリエの方法($x=0$ における $\lbrace p(0), p^{(1)}(0), p^{(2)}(0), \dots, p^{(9)}(0) \rbrace$ の符号変化の数と、$x=1$ における $\lbrace p(1), p^{(1)}(1), p^{(2)}(1), \dots, p^{(9)}(1) \rbrace$ の符号変化の数の差を用いる)は実装が面倒だったので、ブダンの方法($p(x+0)$ と $p(x+1)$ の係数の符号変化の数の差を用いる)に変更しました。
$p(x+1)$ の係数を求める式はSage Mathで求め、そのまま実装しました。
var('x a0 a1 a2 a3 a4 a5 a6 a7 a8 a9')
x1=x+1
p=a0*x1^9+a1*x1^8+a2*x1^7+a3*x1^6+a4*x1^5+a5*x1^4+a6*x1^3+a7*x1^2+a8*x1+a9
p=p.simplify_full()
p.coefficients(x)
[[a0 + a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8 + a9, 0],
[9*a0 + 8*a1 + 7*a2 + 6*a3 + 5*a4 + 4*a5 + 3*a6 + 2*a7 + a8, 1],
[36*a0 + 28*a1 + 21*a2 + 15*a3 + 10*a4 + 6*a5 + 3*a6 + a7, 2],
[84*a0 + 56*a1 + 35*a2 + 20*a3 + 10*a4 + 4*a5 + a6, 3],
[126*a0 + 70*a1 + 35*a2 + 15*a3 + 5*a4 + a5, 4],
[126*a0 + 56*a1 + 21*a2 + 6*a3 + a4, 5],
[84*a0 + 28*a1 + 7*a2 + a3, 6],
[36*a0 + 8*a1 + a2, 7],
[9*a0 + a1, 8],
[a0, 9]]
VAG法の多項式 $ (x+1)^9 p \left (\frac{a+bx}{1+x} \right ) $ の係数を求める式もSage Mathで求めました。ただし、こちらは9次式となり計算誤差が怖いので、乗算と加算を繰り返す形にアレンジして実装しました。
var('x a b a0 a1 a2 a3 a4 a5 a6 a7 a8 a9')
x1=(a+b*x)/(1+x)
p=(a0*x1^9+a1*x1^8+a2*x1^7+a3*x1^6+a4*x1^5+a5*x1^4+a6*x1^3+a7*x1^2+a8*x1+a9)*(x+1)^9
p=p.simplify_full()
p.coefficients(x)
[[a^9*a0 + a^8*a1 + a^7*a2 + a^6*a3 + a^5*a4 + a^4*a5 + a^3*a6 + a^2*a7 + a*a8 + a9,
0],
[a^8*a1 + 2*a^7*a2 + 3*a^6*a3 + 4*a^5*a4 + 5*a^4*a5 + 6*a^3*a6 + 7*a^2*a7 + 8*a*a8 + (9*a^8*a0 + 8*a^7*a1 + 7*a^6*a2 + 6*a^5*a3 + 5*a^4*a4 + 4*a^3*a5 + 3*a^2*a6 + 2*a*a7 + a8)*b + 9*a9,
1],
[a^7*a2 + 3*a^6*a3 + 6*a^5*a4 + 10*a^4*a5 + 15*a^3*a6 + 21*a^2*a7 + (36*a^7*a0 + 28*a^6*a1 + 21*a^5*a2 + 15*a^4*a3 + 10*a^3*a4 + 6*a^2*a5 + 3*a*a6 + a7)*b^2 + 28*a*a8 + 2*(4*a^7*a1 + 7*a^6*a2 + 9*a^5*a3 + 10*a^4*a4 + 10*a^3*a5 + 9*a^2*a6 + 7*a*a7 + 4*a8)*b + 36*a9,
2],
[a^6*a3 + 4*a^5*a4 + 10*a^4*a5 + 20*a^3*a6 + (84*a^6*a0 + 56*a^5*a1 + 35*a^4*a2 + 20*a^3*a3 + 10*a^2*a4 + 4*a*a5 + a6)*b^3 + 35*a^2*a7 + (28*a^6*a1 + 42*a^5*a2 + 45*a^4*a3 + 40*a^3*a4 + 30*a^2*a5 + 18*a*a6 + 7*a7)*b^2 + 56*a*a8 + (7*a^6*a2 + 18*a^5*a3 + 30*a^4*a4 + 40*a^3*a5 + 45*a^2*a6 + 42*a*a7 + 28*a8)*b + 84*a9,
3],
[a^5*a4 + 5*a^4*a5 + (126*a^5*a0 + 70*a^4*a1 + 35*a^3*a2 + 15*a^2*a3 + 5*a*a4 + a5)*b^4 + 15*a^3*a6 + 2*(28*a^5*a1 + 35*a^4*a2 + 30*a^3*a3 + 20*a^2*a4 + 10*a*a5 + 3*a6)*b^3 + 35*a^2*a7 + 3*(7*a^5*a2 + 15*a^4*a3 + 20*a^3*a4 + 20*a^2*a5 + 15*a*a6 + 7*a7)*b^2 + 70*a*a8 + 2*(3*a^5*a3 + 10*a^4*a4 + 20*a^3*a5 + 30*a^2*a6 + 35*a*a7 + 28*a8)*b + 126*a9,
4],
[(126*a^4*a0 + 56*a^3*a1 + 21*a^2*a2 + 6*a*a3 + a4)*b^5 + a^4*a5 + 5*(14*a^4*a1 + 14*a^3*a2 + 9*a^2*a3 + 4*a*a4 + a5)*b^4 + 6*a^3*a6 + 5*(7*a^4*a2 + 12*a^3*a3 + 12*a^2*a4 + 8*a*a5 + 3*a6)*b^3 + 21*a^2*a7 + 5*(3*a^4*a3 + 8*a^3*a4 + 12*a^2*a5 + 12*a*a6 + 7*a7)*b^2 + 56*a*a8 + 5*(a^4*a4 + 4*a^3*a5 + 9*a^2*a6 + 14*a*a7 + 14*a8)*b + 126*a9,
5],
[(84*a^3*a0 + 28*a^2*a1 + 7*a*a2 + a3)*b^6 + 2*(28*a^3*a1 + 21*a^2*a2 + 9*a*a3 + 2*a4)*b^5 + 5*(7*a^3*a2 + 9*a^2*a3 + 6*a*a4 + 2*a5)*b^4 + a^3*a6 + 20*(a^3*a3 + 2*a^2*a4 + 2*a*a5 + a6)*b^3 + 7*a^2*a7 + 5*(2*a^3*a4 + 6*a^2*a5 + 9*a*a6 + 7*a7)*b^2 + 28*a*a8 + 2*(2*a^3*a5 + 9*a^2*a6 + 21*a*a7 + 28*a8)*b + 84*a9,
6],
[(36*a^2*a0 + 8*a*a1 + a2)*b^7 + (28*a^2*a1 + 14*a*a2 + 3*a3)*b^6 + 3*(7*a^2*a2 + 6*a*a3 + 2*a4)*b^5 + 5*(3*a^2*a3 + 4*a*a4 + 2*a5)*b^4 + 5*(2*a^2*a4 + 4*a*a5 + 3*a6)*b^3 + a^2*a7 + 3*(2*a^2*a5 + 6*a*a6 + 7*a7)*b^2 + 8*a*a8 + (3*a^2*a6 + 14*a*a7 + 28*a8)*b + 36*a9,
7],
[(9*a*a0 + a1)*b^8 + 2*(4*a*a1 + a2)*b^7 + (7*a*a2 + 3*a3)*b^6 + 2*(3*a*a3 + 2*a4)*b^5 + 5*(a*a4 + a5)*b^4 + 2*(2*a*a5 + 3*a6)*b^3 + (3*a*a6 + 7*a7)*b^2 + a*a8 + 2*(a*a7 + 4*a8)*b + 9*a9,
8],
[a0*b^9 + a1*b^8 + a2*b^7 + a3*b^6 + a4*b^5 + a5*b^4 + a6*b^3 + a7*b^2 + a8*b + a9,
9]]
実装例
この手の処理の動作環境を想定するに、なるべく素のものが良いだろうと考えc++、ただし高度な(?)機能をなるべく使わずに実装した例は以下の通りです。
今回、Qtで動作確認したので入口と出口にQListとQPointFを使っていますが、大した使い方ではないので、他へ容易に移行できると思います。
ベジェ曲線にスペシフィックな処理は係数を求める箇所だけなので、他の3次パラメトリック曲線(B-スプラインやCatmull-Rom曲線など)にも容易に適用できると思います。
前回申告(?)した課題は未対応です。重根があるとVAGが暴走すると思います。
#include <cmath>
#include <QPointF>
#include <QList>
using namespace std;
#define PW3(x) ((x)*(x)*(x))
#define PW2(x) ((x)*(x))
typedef struct{
double a; // 区間from
double b; // 区間to
double pa; // aの関数値
double pb; // bの関数値
}Interval;
// 3次ベジェ曲線の係数を求める
void coefBezier(
QList<QPointF> &cp, // IN ベジェ曲線 制御点
double *a, // OUT x係数
double *b) // OUT y係数
{
a[0]=-cp[0].x()+3*cp[1].x()-3*cp[2].x()+cp[3].x();
a[1]=3*cp[0].x()-6*cp[1].x()+3*cp[2].x();
a[2]=-3*cp[0].x()+3*cp[1].x();
a[3]=cp[0].x();
b[0]=-cp[0].y()+3*cp[1].y()-3*cp[2].y()+cp[3].y();
b[1]=3*cp[0].y()-6*cp[1].y()+3*cp[2].y();
b[2]=-3*cp[0].y()+3*cp[1].y();
b[3]=cp[0].y();
}
// 3次パラメトリック曲線の座標を求める
QPointF pointBezier(
double *a, // IN x係数
double *b, // IN y係数
double t) // IN パラメータ
{
return QPointF(a[0]*PW3(t)+a[1]*PW2(t)+a[2]*t+a[3],
b[0]*PW3(t)+b[1]*PW2(t)+b[2]*t+b[3]);
}
// 3次パラメトリック曲線どうしの交点の陰伏方程式F0(u)の係数を求める
void coefImp0(
double *a, // IN 曲線0 (x,y)=f(t)の係数列 a[0],b[0]が3次項の係数
double *b,
double *c, // IN 曲線1 (x,y)=g(u)の係数列 c[0],d[0]が3次項の係数
double *d,
double *cf) // OUT F0(u)の係数列 cf[0]が9次項の係数
{
cf[0]=-PW3(b[0])*PW3(c[0])+3*a[0]*PW2(b[0])*PW2(c[0])*d[0]-3*PW2(a[0])*b[0]*c[0]*PW2(d[0])+PW3(a[0])*PW3(d[0]);
cf[1]=-3*PW3(b[0])*PW2(c[0])*c[1]+6*a[0]*PW2(b[0])*c[0]*c[1]*d[0]-3*PW2(a[0])*b[0]*c[1]*PW2(d[0])+3*(a[0]*PW2(b[0])*PW2(c[0])-2*PW2(a[0])*b[0]*c[0]*d[0]+PW3(a[0])*PW2(d[0]))*d[1];
cf[2]=-3*PW3(b[0])*c[0]*PW2(c[1])-3*PW3(b[0])*PW2(c[0])*c[2]-3*PW2(a[0])*b[0]*c[2]*PW2(d[0])-3*(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*PW2(d[1])+3*(a[0]*PW2(b[0])*PW2(c[1])+2*a[0]*PW2(b[0])*c[0]*c[2])*d[0]+6*(a[0]*PW2(b[0])*c[0]*c[1]-PW2(a[0])*b[0]*c[1]*d[0])*d[1]+3*(a[0]*PW2(b[0])*PW2(c[0])-2*PW2(a[0])*b[0]*c[0]*d[0]+PW3(a[0])*PW2(d[0]))*d[2];
cf[3]=-PW3(b[0])*PW3(c[1])-6*PW3(b[0])*c[0]*c[1]*c[2]-3*PW3(b[0])*PW2(c[0])*c[3]-3*PW2(a[0])*b[0]*c[1]*PW2(d[1])+PW3(a[0])*PW3(d[1])+(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*PW2(c[0])+(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*PW2(d[0])+(6*a[0]*PW2(b[0])*c[1]*c[2]+6*a[0]*PW2(b[0])*c[0]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[0])*d[0]+3*(a[0]*PW2(b[0])*PW2(c[1])+2*a[0]*PW2(b[0])*c[0]*c[2]-2*PW2(a[0])*b[0]*c[2]*d[0])*d[1]+6*(a[0]*PW2(b[0])*c[0]*c[1]-PW2(a[0])*b[0]*c[1]*d[0]-(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*d[1])*d[2]+3*(a[0]*PW2(b[0])*PW2(c[0])-2*PW2(a[0])*b[0]*c[0]*d[0]+PW3(a[0])*PW2(d[0]))*d[3];
cf[4]=-3*PW3(b[0])*PW2(c[1])*c[2]-3*PW3(b[0])*c[0]*PW2(c[2])-6*PW3(b[0])*c[0]*c[1]*c[3]-3*PW2(a[0])*b[0]*c[2]*PW2(d[1])+2*(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[0]*c[1]-3*(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*PW2(d[2])+(3*a[0]*PW2(b[0])*PW2(c[2])+6*a[0]*PW2(b[0])*c[1]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[1])*d[0]+(6*a[0]*PW2(b[0])*c[1]*c[2]+6*a[0]*PW2(b[0])*c[0]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[0]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[0])*d[1]+3*(a[0]*PW2(b[0])*PW2(c[1])+2*a[0]*PW2(b[0])*c[0]*c[2]-2*PW2(a[0])*b[0]*c[2]*d[0]-2*PW2(a[0])*b[0]*c[1]*d[1]+PW3(a[0])*PW2(d[1]))*d[2]+6*(a[0]*PW2(b[0])*c[0]*c[1]-PW2(a[0])*b[0]*c[1]*d[0]-(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*d[1])*d[3];
cf[5]=-3*PW3(b[0])*c[1]*PW2(c[2])+(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*PW2(c[1])+2*(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[0]*c[2]+(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*PW2(d[1])-3*(PW2(a[0])*b[0]*c[1]-PW3(a[0])*d[1])*PW2(d[2])-3*(PW3(b[0])*PW2(c[1])+2*PW3(b[0])*c[0]*c[2])*c[3]+(6*a[0]*PW2(b[0])*c[2]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[2])*d[0]+(3*a[0]*PW2(b[0])*PW2(c[2])+6*a[0]*PW2(b[0])*c[1]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[1])*d[1]+(6*a[0]*PW2(b[0])*c[1]*c[2]+6*a[0]*PW2(b[0])*c[0]*c[3]-6*PW2(a[0])*b[0]*c[2]*d[1]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[0]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[0])*d[2]+3*(a[0]*PW2(b[0])*PW2(c[1])+2*a[0]*PW2(b[0])*c[0]*c[2]-2*PW2(a[0])*b[0]*c[2]*d[0]-2*PW2(a[0])*b[0]*c[1]*d[1]+PW3(a[0])*PW2(d[1])-2*(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*d[2])*d[3];
cf[6]=-PW3(b[0])*PW3(c[2])-3*PW3(b[0])*c[0]*PW2(c[3])-3*PW2(a[0])*b[0]*c[2]*PW2(d[2])+PW3(a[0])*PW3(d[2])+2*(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[1]*c[2]-3*(PW2(a[0])*b[0]*c[0]-PW3(a[0])*d[0])*PW2(d[3])-(3*PW2(a[3])*PW3(b[0])-2*a[2]*a[3]*PW2(b[0])*b[1]+2*a[1]*a[3]*b[0]*PW2(b[1])-2*a[0]*a[3]*PW3(b[1])+PW2(a[0])*PW3(b[2])+3*PW2(a[0])*b[0]*PW2(b[3])-(a[0]*a[1]*b[1]-(PW2(a[1])-2*a[0]*a[2])*b[0])*PW2(b[2])+(a[0]*a[2]*PW2(b[1])+(PW2(a[2])-4*a[1]*a[3])*PW2(b[0])-(a[1]*a[2]-6*a[0]*a[3])*b[0]*b[1])*b[2]+(2*a[0]*a[1]*PW2(b[1])+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*b[3])*c[0]-2*(3*PW3(b[0])*c[1]*c[2]-(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[0])*c[3]+(PW2(a[0])*a[2]*PW2(b[2])+3*PW3(a[0])*PW2(b[3])+3*a[0]*PW2(b[0])*PW2(c[3])+(PW3(a[2])-3*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3]))*PW2(b[0])-(a[1]*PW2(a[2])-(2*PW2(a[1])+a[0]*a[2])*a[3])*b[0]*b[1]+(a[0]*PW2(a[2])-2*a[0]*a[1]*a[3])*PW2(b[1])+((PW2(a[1])*a[2]-2*a[0]*PW2(a[2])-a[0]*a[1]*a[3])*b[0]-(a[0]*a[1]*a[2]-3*PW2(a[0])*a[3])*b[1])*b[2]-2*(PW2(a[0])*a[1]*b[2]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*b[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[3])*d[0]+(6*a[0]*PW2(b[0])*c[2]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[2])*d[1]+(3*a[0]*PW2(b[0])*PW2(c[2])+6*a[0]*PW2(b[0])*c[1]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[1]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[1])*d[2]+(6*a[0]*PW2(b[0])*c[1]*c[2]+6*a[0]*PW2(b[0])*c[0]*c[3]-6*PW2(a[0])*b[0]*c[2]*d[1]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[0]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[0]-6*(PW2(a[0])*b[0]*c[1]-PW3(a[0])*d[1])*d[2])*d[3];
cf[7]=-3*PW3(b[0])*c[1]*PW2(c[3])+(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*PW2(c[2])+(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*PW2(d[2])-3*(PW2(a[0])*b[0]*c[1]-PW3(a[0])*d[1])*PW2(d[3])-(3*PW2(a[3])*PW3(b[0])-2*a[2]*a[3]*PW2(b[0])*b[1]+2*a[1]*a[3]*b[0]*PW2(b[1])-2*a[0]*a[3]*PW3(b[1])+PW2(a[0])*PW3(b[2])+3*PW2(a[0])*b[0]*PW2(b[3])-(a[0]*a[1]*b[1]-(PW2(a[1])-2*a[0]*a[2])*b[0])*PW2(b[2])+(a[0]*a[2]*PW2(b[1])+(PW2(a[2])-4*a[1]*a[3])*PW2(b[0])-(a[1]*a[2]-6*a[0]*a[3])*b[0]*b[1])*b[2]+(2*a[0]*a[1]*PW2(b[1])+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*b[3])*c[1]-(3*PW3(b[0])*PW2(c[2])-2*(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[1])*c[3]+(PW2(a[0])*a[2]*PW2(b[2])+3*PW3(a[0])*PW2(b[3])+3*a[0]*PW2(b[0])*PW2(c[3])+(PW3(a[2])-3*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3]))*PW2(b[0])-(a[1]*PW2(a[2])-(2*PW2(a[1])+a[0]*a[2])*a[3])*b[0]*b[1]+(a[0]*PW2(a[2])-2*a[0]*a[1]*a[3])*PW2(b[1])+((PW2(a[1])*a[2]-2*a[0]*PW2(a[2])-a[0]*a[1]*a[3])*b[0]-(a[0]*a[1]*a[2]-3*PW2(a[0])*a[3])*b[1])*b[2]-2*(PW2(a[0])*a[1]*b[2]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*b[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[3])*d[1]+(6*a[0]*PW2(b[0])*c[2]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[2])*d[2]+(3*a[0]*PW2(b[0])*PW2(c[2])+6*a[0]*PW2(b[0])*c[1]*c[3]-6*PW2(a[0])*b[0]*c[2]*d[2]+3*PW3(a[0])*PW2(d[2])+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[1]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[1])*d[3];
cf[8]=-3*PW3(b[0])*c[2]*PW2(c[3])+2*(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*c[2]*c[3]-3*(PW2(a[0])*b[0]*c[2]-PW3(a[0])*d[2])*PW2(d[3])-(3*PW2(a[3])*PW3(b[0])-2*a[2]*a[3]*PW2(b[0])*b[1]+2*a[1]*a[3]*b[0]*PW2(b[1])-2*a[0]*a[3]*PW3(b[1])+PW2(a[0])*PW3(b[2])+3*PW2(a[0])*b[0]*PW2(b[3])-(a[0]*a[1]*b[1]-(PW2(a[1])-2*a[0]*a[2])*b[0])*PW2(b[2])+(a[0]*a[2]*PW2(b[1])+(PW2(a[2])-4*a[1]*a[3])*PW2(b[0])-(a[1]*a[2]-6*a[0]*a[3])*b[0]*b[1])*b[2]+(2*a[0]*a[1]*PW2(b[1])+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*b[3])*c[2]+(PW2(a[0])*a[2]*PW2(b[2])+3*PW3(a[0])*PW2(b[3])+3*a[0]*PW2(b[0])*PW2(c[3])+(PW3(a[2])-3*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3]))*PW2(b[0])-(a[1]*PW2(a[2])-(2*PW2(a[1])+a[0]*a[2])*a[3])*b[0]*b[1]+(a[0]*PW2(a[2])-2*a[0]*a[1]*a[3])*PW2(b[1])+((PW2(a[1])*a[2]-2*a[0]*PW2(a[2])-a[0]*a[1]*a[3])*b[0]-(a[0]*a[1]*a[2]-3*PW2(a[0])*a[3])*b[1])*b[2]-2*(PW2(a[0])*a[1]*b[2]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*b[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[3])*d[2]+(6*a[0]*PW2(b[0])*c[2]*c[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[2]+2*(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*d[2])*d[3];
cf[9]=PW3(a[3])*PW3(b[0])-a[2]*PW2(a[3])*PW2(b[0])*b[1]+a[1]*PW2(a[3])*b[0]*PW2(b[1])-a[0]*PW2(a[3])*PW3(b[1])+PW2(a[0])*a[3]*PW3(b[2])-PW3(a[0])*PW3(b[3])-PW3(b[0])*PW3(c[3])+PW3(a[0])*PW3(d[3])-(a[0]*a[1]*a[3]*b[1]-(PW2(a[1])-2*a[0]*a[2])*a[3]*b[0])*PW2(b[2])+(PW2(a[0])*a[1]*b[2]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*PW2(b[3])+(3*a[3]*PW3(b[0])-a[2]*PW2(b[0])*b[1]+a[1]*b[0]*PW2(b[1])-a[0]*PW3(b[1])-3*a[0]*PW2(b[0])*b[3]-(2*a[1]*PW2(b[0])-3*a[0]*b[0]*b[1])*b[2])*PW2(c[3])+(PW2(a[0])*a[1]*b[2]-3*PW3(a[0])*b[3]-3*PW2(a[0])*b[0]*c[3]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*PW2(d[3])+(a[0]*a[2]*a[3]*PW2(b[1])+(PW2(a[2])*a[3]-2*a[1]*PW2(a[3]))*PW2(b[0])-(a[1]*a[2]*a[3]-3*a[0]*PW2(a[3]))*b[0]*b[1])*b[2]-(PW2(a[0])*a[2]*PW2(b[2])+(PW3(a[2])-3*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3]))*PW2(b[0])-(a[1]*PW2(a[2])-(2*PW2(a[1])+a[0]*a[2])*a[3])*b[0]*b[1]+(a[0]*PW2(a[2])-2*a[0]*a[1]*a[3])*PW2(b[1])+((PW2(a[1])*a[2]-2*a[0]*PW2(a[2])-a[0]*a[1]*a[3])*b[0]-(a[0]*a[1]*a[2]-3*PW2(a[0])*a[3])*b[1])*b[2])*b[3]-(3*PW2(a[3])*PW3(b[0])-2*a[2]*a[3]*PW2(b[0])*b[1]+2*a[1]*a[3]*b[0]*PW2(b[1])-2*a[0]*a[3]*PW3(b[1])+PW2(a[0])*PW3(b[2])+3*PW2(a[0])*b[0]*PW2(b[3])-(a[0]*a[1]*b[1]-(PW2(a[1])-2*a[0]*a[2])*b[0])*PW2(b[2])+(a[0]*a[2]*PW2(b[1])+(PW2(a[2])-4*a[1]*a[3])*PW2(b[0])-(a[1]*a[2]-6*a[0]*a[3])*b[0]*b[1])*b[2]+(2*a[0]*a[1]*PW2(b[1])+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*b[3])*c[3]+(PW2(a[0])*a[2]*PW2(b[2])+3*PW3(a[0])*PW2(b[3])+3*a[0]*PW2(b[0])*PW2(c[3])+(PW3(a[2])-3*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3]))*PW2(b[0])-(a[1]*PW2(a[2])-(2*PW2(a[1])+a[0]*a[2])*a[3])*b[0]*b[1]+(a[0]*PW2(a[2])-2*a[0]*a[1]*a[3])*PW2(b[1])+((PW2(a[1])*a[2]-2*a[0]*PW2(a[2])-a[0]*a[1]*a[3])*b[0]-(a[0]*a[1]*a[2]-3*PW2(a[0])*a[3])*b[1])*b[2]-2*(PW2(a[0])*a[1]*b[2]+(PW3(a[1])-3*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3])*b[0]-(a[0]*PW2(a[1])-2*PW2(a[0])*a[2])*b[1])*b[3]+(2*a[0]*a[1]*PW2(b[1])+6*PW2(a[0])*b[0]*b[3]+3*(a[1]*a[2]-2*a[0]*a[3])*PW2(b[0])-(2*PW2(a[1])+a[0]*a[2])*b[0]*b[1]+(a[0]*a[1]*b[0]-3*PW2(a[0])*b[1])*b[2])*c[3])*d[3];
}
// 3次パラメトリック曲線どうしの交点の陰伏方程式F1(t)の係数を求める
void coefImp1(
double *a, // IN 曲線0 (x,y)=f(t)の係数列 a[0],b[0]が3次項の係数
double *b,
double *c, // IN 曲線1 (x,y)=g(u)の係数列 c[0],d[0]が3次項の係数
double *d,
double *cf) // OUT F1(t)の係数列 cf[0]が9次項の係数
{
cf[0]=PW3(b[0])*PW3(c[0])-3*a[0]*PW2(b[0])*PW2(c[0])*d[0]+3*PW2(a[0])*b[0]*c[0]*PW2(d[0])-PW3(a[0])*PW3(d[0]);
cf[1]=3*PW2(b[0])*b[1]*PW3(c[0])-3*PW2(a[0])*a[1]*PW3(d[0])-3*(a[1]*PW2(b[0])+2*a[0]*b[0]*b[1])*PW2(c[0])*d[0]+3*(2*a[0]*a[1]*b[0]+PW2(a[0])*b[1])*c[0]*PW2(d[0]);
cf[2]=3*(b[0]*PW2(b[1])+PW2(b[0])*b[2])*PW3(c[0])-3*(a[2]*PW2(b[0])+2*a[1]*b[0]*b[1]+a[0]*PW2(b[1])+2*a[0]*b[0]*b[2])*PW2(c[0])*d[0]+3*(2*a[0]*a[1]*b[1]+PW2(a[0])*b[2]+(PW2(a[1])+2*a[0]*a[2])*b[0])*c[0]*PW2(d[0])-3*(a[0]*PW2(a[1])+PW2(a[0])*a[2])*PW3(d[0]);
cf[3]=-PW2(a[0])*c[0]*PW3(d[1])+(PW3(b[1])+6*b[0]*b[1]*b[2]+3*PW2(b[0])*b[3])*PW3(c[0])-(PW3(a[1])+6*a[0]*a[1]*a[2]+3*PW2(a[0])*a[3]-3*PW2(a[0])*c[3])*PW3(d[0])+3*(a[0]*b[0]*c[1]*c[2]-2*a[0]*b[0]*c[0]*c[3]+(2*a[0]*a[1]*b[2]+PW2(a[0])*b[3]+2*(a[1]*a[2]+a[0]*a[3])*b[0]+(PW2(a[1])+2*a[0]*a[2])*b[1])*c[0])*PW2(d[0])+(2*a[0]*b[0]*c[0]*c[1]+PW2(a[0])*c[1]*d[0])*PW2(d[1])+(PW2(b[0])*PW3(c[1])-3*PW2(b[0])*c[0]*c[1]*c[2]+3*PW2(b[0])*PW2(c[0])*c[3]-3*(a[3]*PW2(b[0])+2*a[2]*b[0]*b[1]+a[1]*PW2(b[1])+2*a[0]*b[0]*b[3]+2*(a[1]*b[0]+a[0]*b[1])*b[2])*PW2(c[0]))*d[0]-(PW2(b[0])*c[0]*PW2(c[1])-2*PW2(b[0])*PW2(c[0])*c[2]+PW2(a[0])*c[2]*PW2(d[0])+(2*a[0]*b[0]*PW2(c[1])+a[0]*b[0]*c[0]*c[2])*d[0])*d[1]+(PW2(b[0])*PW2(c[0])*c[1]+a[0]*b[0]*c[0]*c[1]*d[0]-2*PW2(a[0])*c[1]*PW2(d[0])-3*(a[0]*b[0]*PW2(c[0])-PW2(a[0])*c[0]*d[0])*d[1])*d[2]-3*(PW2(b[0])*PW3(c[0])-2*a[0]*b[0]*PW2(c[0])*d[0]+PW2(a[0])*c[0]*PW2(d[0]))*d[3];
cf[4]=-2*a[0]*a[1]*c[0]*PW3(d[1])+3*(PW2(b[1])*b[2]+b[0]*PW2(b[2])+2*b[0]*b[1]*b[3])*PW3(c[0])-3*(PW2(a[1])*a[2]+a[0]*PW2(a[2])+2*a[0]*a[1]*a[3]-2*a[0]*a[1]*c[3])*PW3(d[0])+3*((a[1]*b[0]+a[0]*b[1])*c[1]*c[2]-2*(a[1]*b[0]+a[0]*b[1])*c[0]*c[3]+(2*a[0]*a[1]*b[3]+(PW2(a[2])+2*a[1]*a[3])*b[0]+2*(a[1]*a[2]+a[0]*a[3])*b[1]+(PW2(a[1])+2*a[0]*a[2])*b[2])*c[0])*PW2(d[0])+2*(a[0]*a[1]*c[1]*d[0]+(a[1]*b[0]+a[0]*b[1])*c[0]*c[1])*PW2(d[1])+(2*b[0]*b[1]*PW3(c[1])-6*b[0]*b[1]*c[0]*c[1]*c[2]+6*b[0]*b[1]*PW2(c[0])*c[3]-3*(2*a[3]*b[0]*b[1]+a[2]*PW2(b[1])+a[0]*PW2(b[2])+2*(a[2]*b[0]+a[1]*b[1])*b[2]+2*(a[1]*b[0]+a[0]*b[1])*b[3])*PW2(c[0]))*d[0]-(2*b[0]*b[1]*c[0]*PW2(c[1])-4*b[0]*b[1]*PW2(c[0])*c[2]+2*a[0]*a[1]*c[2]*PW2(d[0])+(2*(a[1]*b[0]+a[0]*b[1])*PW2(c[1])+(a[1]*b[0]+a[0]*b[1])*c[0]*c[2])*d[0])*d[1]+(2*b[0]*b[1]*PW2(c[0])*c[1]-4*a[0]*a[1]*c[1]*PW2(d[0])+(a[1]*b[0]+a[0]*b[1])*c[0]*c[1]*d[0]+3*(2*a[0]*a[1]*c[0]*d[0]-(a[1]*b[0]+a[0]*b[1])*PW2(c[0]))*d[1])*d[2]-6*(b[0]*b[1]*PW3(c[0])+a[0]*a[1]*c[0]*PW2(d[0])-(a[1]*b[0]+a[0]*b[1])*PW2(c[0])*d[0])*d[3];
cf[5]=-(PW2(a[1])+2*a[0]*a[2])*c[0]*PW3(d[1])+3*(b[1]*PW2(b[2])+(PW2(b[1])+2*b[0]*b[2])*b[3])*PW3(c[0])-3*(a[1]*PW2(a[2])+(PW2(a[1])+2*a[0]*a[2])*a[3]-(PW2(a[1])+2*a[0]*a[2])*c[3])*PW3(d[0])+3*((a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[1]*c[2]-2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[0]*c[3]+(2*a[2]*a[3]*b[0]+(PW2(a[2])+2*a[1]*a[3])*b[1]+2*(a[1]*a[2]+a[0]*a[3])*b[2]+(PW2(a[1])+2*a[0]*a[2])*b[3])*c[0])*PW2(d[0])+(2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[0]*c[1]+(PW2(a[1])+2*a[0]*a[2])*c[1]*d[0])*PW2(d[1])+((PW2(b[1])+2*b[0]*b[2])*PW3(c[1])-3*(PW2(b[1])+2*b[0]*b[2])*c[0]*c[1]*c[2]+3*(PW2(b[1])+2*b[0]*b[2])*PW2(c[0])*c[3]-3*(a[3]*PW2(b[1])+a[1]*PW2(b[2])+2*(a[3]*b[0]+a[2]*b[1])*b[2]+2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*b[3])*PW2(c[0]))*d[0]-((PW2(b[1])+2*b[0]*b[2])*c[0]*PW2(c[1])-2*(PW2(b[1])+2*b[0]*b[2])*PW2(c[0])*c[2]+(PW2(a[1])+2*a[0]*a[2])*c[2]*PW2(d[0])+(2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*PW2(c[1])+(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[0]*c[2])*d[0])*d[1]+((PW2(b[1])+2*b[0]*b[2])*PW2(c[0])*c[1]+(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*c[0]*c[1]*d[0]-2*(PW2(a[1])+2*a[0]*a[2])*c[1]*PW2(d[0])-3*((a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*PW2(c[0])-(PW2(a[1])+2*a[0]*a[2])*c[0]*d[0])*d[1])*d[2]-3*((PW2(b[1])+2*b[0]*b[2])*PW3(c[0])-2*(a[2]*b[0]+a[1]*b[1]+a[0]*b[2])*PW2(c[0])*d[0]+(PW2(a[1])+2*a[0]*a[2])*c[0]*PW2(d[0]))*d[3];
cf[6]=-a[0]*PW2(c[0])*PW3(d[2])+(PW3(b[2])+6*b[1]*b[2]*b[3]+3*b[0]*PW2(b[3]))*PW3(c[0])-(PW3(a[2])+6*a[1]*a[2]*a[3]+3*a[0]*PW2(a[3])+3*a[0]*PW2(c[3])-6*(a[1]*a[2]+a[0]*a[3])*c[3])*PW3(d[0])+2*(a[0]*c[0]*c[3]-(a[1]*a[2]+a[0]*a[3])*c[0])*PW3(d[1])+(b[0]*PW3(c[2])+3*b[0]*c[0]*PW2(c[3])+3*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[1]*c[2]+3*(PW2(a[3])*b[0]+2*a[2]*a[3]*b[1]+(PW2(a[2])+2*a[1]*a[3])*b[2]+2*(a[1]*a[2]+a[0]*a[3])*b[3])*c[0]-3*(b[0]*c[1]*c[2]+2*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[0])*c[3])*PW2(d[0])+(b[0]*c[0]*PW2(c[2])-2*b[0]*c[0]*c[1]*c[3]+2*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[0]*c[1]-2*(a[0]*c[1]*c[3]-(a[1]*a[2]+a[0]*a[3])*c[1])*d[0])*PW2(d[1])+(b[0]*PW2(c[0])*c[2]+a[0]*c[0]*c[1]*d[1]-(a[0]*PW2(c[1])-2*a[0]*c[0]*c[2])*d[0])*PW2(d[2])+3*(b[0]*PW3(c[0])-a[0]*PW2(c[0])*d[0])*PW2(d[3])+(2*(b[1]*b[2]+b[0]*b[3])*PW3(c[1])-6*(b[1]*b[2]+b[0]*b[3])*c[0]*c[1]*c[2]+6*(b[1]*b[2]+b[0]*b[3])*PW2(c[0])*c[3]-3*(2*a[3]*b[1]*b[2]+a[2]*PW2(b[2])+a[0]*PW2(b[3])+2*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2])*b[3])*PW2(c[0]))*d[0]-(2*(b[1]*b[2]+b[0]*b[3])*c[0]*PW2(c[1])-4*(b[1]*b[2]+b[0]*b[3])*PW2(c[0])*c[2]-2*(a[0]*c[2]*c[3]-(a[1]*a[2]+a[0]*a[3])*c[2])*PW2(d[0])+(b[0]*c[1]*PW2(c[2])+2*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*PW2(c[1])+(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[0]*c[2]-(2*b[0]*PW2(c[1])+b[0]*c[0]*c[2])*c[3])*d[0])*d[1]-(a[0]*c[0]*c[2]*PW2(d[1])-2*(b[1]*b[2]+b[0]*b[3])*PW2(c[0])*c[1]+(a[0]*PW2(c[2])-4*a[0]*c[1]*c[3]+4*(a[1]*a[2]+a[0]*a[3])*c[1])*PW2(d[0])-(b[0]*PW2(c[1])*c[2]-2*b[0]*c[0]*PW2(c[2])-b[0]*c[0]*c[1]*c[3]+(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*c[0]*c[1])*d[0]+(b[0]*c[0]*c[1]*c[2]-3*b[0]*PW2(c[0])*c[3]+3*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*PW2(c[0])-(a[0]*c[1]*c[2]-6*a[0]*c[0]*c[3]+6*(a[1]*a[2]+a[0]*a[3])*c[0])*d[0])*d[1])*d[2]-(2*a[0]*c[0]*c[1]*PW2(d[1])+6*(b[1]*b[2]+b[0]*b[3])*PW3(c[0])+3*(a[0]*c[1]*c[2]-2*a[0]*c[0]*c[3]+2*(a[1]*a[2]+a[0]*a[3])*c[0])*PW2(d[0])+2*(b[0]*PW3(c[1])-3*b[0]*c[0]*c[1]*c[2]+3*b[0]*PW2(c[0])*c[3]-3*(a[3]*b[0]+a[2]*b[1]+a[1]*b[2]+a[0]*b[3])*PW2(c[0]))*d[0]-(2*b[0]*c[0]*PW2(c[1])-4*b[0]*PW2(c[0])*c[2]+(2*a[0]*PW2(c[1])+a[0]*c[0]*c[2])*d[0])*d[1]+(2*b[0]*PW2(c[0])*c[1]+a[0]*c[0]*c[1]*d[0]-3*a[0]*PW2(c[0])*d[1])*d[2])*d[3];
cf[7]=-a[1]*PW2(c[0])*PW3(d[2])+3*(PW2(b[2])*b[3]+b[1]*PW2(b[3]))*PW3(c[0])-3*(PW2(a[2])*a[3]+a[1]*PW2(a[3])+a[1]*PW2(c[3])-(PW2(a[2])+2*a[1]*a[3])*c[3])*PW3(d[0])+(2*a[1]*c[0]*c[3]-(PW2(a[2])+2*a[1]*a[3])*c[0])*PW3(d[1])+(b[1]*PW3(c[2])+3*b[1]*c[0]*PW2(c[3])+3*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[1]*c[2]+3*(PW2(a[3])*b[1]+2*a[2]*a[3]*b[2]+(PW2(a[2])+2*a[1]*a[3])*b[3])*c[0]-3*(b[1]*c[1]*c[2]+2*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[0])*c[3])*PW2(d[0])+(b[1]*c[0]*PW2(c[2])-2*b[1]*c[0]*c[1]*c[3]+2*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[0]*c[1]-(2*a[1]*c[1]*c[3]-(PW2(a[2])+2*a[1]*a[3])*c[1])*d[0])*PW2(d[1])+(b[1]*PW2(c[0])*c[2]+a[1]*c[0]*c[1]*d[1]-(a[1]*PW2(c[1])-2*a[1]*c[0]*c[2])*d[0])*PW2(d[2])+3*(b[1]*PW3(c[0])-a[1]*PW2(c[0])*d[0])*PW2(d[3])+((PW2(b[2])+2*b[1]*b[3])*PW3(c[1])-3*(PW2(b[2])+2*b[1]*b[3])*c[0]*c[1]*c[2]+3*(PW2(b[2])+2*b[1]*b[3])*PW2(c[0])*c[3]-3*(a[3]*PW2(b[2])+a[1]*PW2(b[3])+2*(a[3]*b[1]+a[2]*b[2])*b[3])*PW2(c[0]))*d[0]-((PW2(b[2])+2*b[1]*b[3])*c[0]*PW2(c[1])-2*(PW2(b[2])+2*b[1]*b[3])*PW2(c[0])*c[2]-(2*a[1]*c[2]*c[3]-(PW2(a[2])+2*a[1]*a[3])*c[2])*PW2(d[0])+(b[1]*c[1]*PW2(c[2])+2*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*PW2(c[1])+(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[0]*c[2]-(2*b[1]*PW2(c[1])+b[1]*c[0]*c[2])*c[3])*d[0])*d[1]-(a[1]*c[0]*c[2]*PW2(d[1])-(PW2(b[2])+2*b[1]*b[3])*PW2(c[0])*c[1]+(a[1]*PW2(c[2])-4*a[1]*c[1]*c[3]+2*(PW2(a[2])+2*a[1]*a[3])*c[1])*PW2(d[0])-(b[1]*PW2(c[1])*c[2]-2*b[1]*c[0]*PW2(c[2])-b[1]*c[0]*c[1]*c[3]+(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*c[0]*c[1])*d[0]+(b[1]*c[0]*c[1]*c[2]-3*b[1]*PW2(c[0])*c[3]+3*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*PW2(c[0])-(a[1]*c[1]*c[2]-6*a[1]*c[0]*c[3]+3*(PW2(a[2])+2*a[1]*a[3])*c[0])*d[0])*d[1])*d[2]-(2*a[1]*c[0]*c[1]*PW2(d[1])+3*(PW2(b[2])+2*b[1]*b[3])*PW3(c[0])+3*(a[1]*c[1]*c[2]-2*a[1]*c[0]*c[3]+(PW2(a[2])+2*a[1]*a[3])*c[0])*PW2(d[0])+2*(b[1]*PW3(c[1])-3*b[1]*c[0]*c[1]*c[2]+3*b[1]*PW2(c[0])*c[3]-3*(a[3]*b[1]+a[2]*b[2]+a[1]*b[3])*PW2(c[0]))*d[0]-(2*b[1]*c[0]*PW2(c[1])-4*b[1]*PW2(c[0])*c[2]+(2*a[1]*PW2(c[1])+a[1]*c[0]*c[2])*d[0])*d[1]+(2*b[1]*PW2(c[0])*c[1]+a[1]*c[0]*c[1]*d[0]-3*a[1]*PW2(c[0])*d[1])*d[2])*d[3];
cf[8]=3*b[2]*PW2(b[3])*PW3(c[0])-a[2]*PW2(c[0])*PW3(d[2])-3*(a[2]*PW2(a[3])-2*a[2]*a[3]*c[3]+a[2]*PW2(c[3]))*PW3(d[0])-2*(a[2]*a[3]*c[0]-a[2]*c[0]*c[3])*PW3(d[1])+(b[2]*PW3(c[2])+3*b[2]*c[0]*PW2(c[3])+3*(a[3]*b[2]+a[2]*b[3])*c[1]*c[2]+3*(PW2(a[3])*b[2]+2*a[2]*a[3]*b[3])*c[0]-3*(b[2]*c[1]*c[2]+2*(a[3]*b[2]+a[2]*b[3])*c[0])*c[3])*PW2(d[0])+(b[2]*c[0]*PW2(c[2])-2*b[2]*c[0]*c[1]*c[3]+2*(a[3]*b[2]+a[2]*b[3])*c[0]*c[1]+2*(a[2]*a[3]*c[1]-a[2]*c[1]*c[3])*d[0])*PW2(d[1])+(b[2]*PW2(c[0])*c[2]+a[2]*c[0]*c[1]*d[1]-(a[2]*PW2(c[1])-2*a[2]*c[0]*c[2])*d[0])*PW2(d[2])+3*(b[2]*PW3(c[0])-a[2]*PW2(c[0])*d[0])*PW2(d[3])+(2*b[2]*b[3]*PW3(c[1])-6*b[2]*b[3]*c[0]*c[1]*c[2]+6*b[2]*b[3]*PW2(c[0])*c[3]-3*(2*a[3]*b[2]*b[3]+a[2]*PW2(b[3]))*PW2(c[0]))*d[0]-(2*b[2]*b[3]*c[0]*PW2(c[1])-4*b[2]*b[3]*PW2(c[0])*c[2]+2*(a[2]*a[3]*c[2]-a[2]*c[2]*c[3])*PW2(d[0])+(b[2]*c[1]*PW2(c[2])+2*(a[3]*b[2]+a[2]*b[3])*PW2(c[1])+(a[3]*b[2]+a[2]*b[3])*c[0]*c[2]-(2*b[2]*PW2(c[1])+b[2]*c[0]*c[2])*c[3])*d[0])*d[1]+(2*b[2]*b[3]*PW2(c[0])*c[1]-a[2]*c[0]*c[2]*PW2(d[1])-(4*a[2]*a[3]*c[1]+a[2]*PW2(c[2])-4*a[2]*c[1]*c[3])*PW2(d[0])+(b[2]*PW2(c[1])*c[2]-2*b[2]*c[0]*PW2(c[2])-b[2]*c[0]*c[1]*c[3]+(a[3]*b[2]+a[2]*b[3])*c[0]*c[1])*d[0]-(b[2]*c[0]*c[1]*c[2]-3*b[2]*PW2(c[0])*c[3]+3*(a[3]*b[2]+a[2]*b[3])*PW2(c[0])-(6*a[2]*a[3]*c[0]+a[2]*c[1]*c[2]-6*a[2]*c[0]*c[3])*d[0])*d[1])*d[2]-(6*b[2]*b[3]*PW3(c[0])+2*a[2]*c[0]*c[1]*PW2(d[1])+3*(2*a[2]*a[3]*c[0]+a[2]*c[1]*c[2]-2*a[2]*c[0]*c[3])*PW2(d[0])+2*(b[2]*PW3(c[1])-3*b[2]*c[0]*c[1]*c[2]+3*b[2]*PW2(c[0])*c[3]-3*(a[3]*b[2]+a[2]*b[3])*PW2(c[0]))*d[0]-(2*b[2]*c[0]*PW2(c[1])-4*b[2]*PW2(c[0])*c[2]+(2*a[2]*PW2(c[1])+a[2]*c[0]*c[2])*d[0])*d[1]+(2*b[2]*PW2(c[0])*c[1]+a[2]*c[0]*c[1]*d[0]-3*a[2]*PW2(c[0])*d[1])*d[2])*d[3];
cf[9]=PW3(b[3])*PW3(c[0])-PW3(c[0])*PW3(d[3])-(PW3(a[3])-3*PW2(a[3])*c[3]+3*a[3]*PW2(c[3])-PW3(c[3]))*PW3(d[0])-(PW2(a[3])*c[0]-2*a[3]*c[0]*c[3]+c[0]*PW2(c[3]))*PW3(d[1])-(a[3]*PW2(c[0])-PW2(c[0])*c[3])*PW3(d[2])+(3*PW2(a[3])*b[3]*c[0]+3*a[3]*b[3]*c[1]*c[2]+b[3]*PW3(c[2])+3*b[3]*c[0]*PW2(c[3])-3*(2*a[3]*b[3]*c[0]+b[3]*c[1]*c[2])*c[3])*PW2(d[0])+(2*a[3]*b[3]*c[0]*c[1]+b[3]*c[0]*PW2(c[2])-2*b[3]*c[0]*c[1]*c[3]+(PW2(a[3])*c[1]-2*a[3]*c[1]*c[3]+c[1]*PW2(c[3]))*d[0])*PW2(d[1])+(b[3]*PW2(c[0])*c[2]-(a[3]*PW2(c[1])-2*a[3]*c[0]*c[2]-(PW2(c[1])-2*c[0]*c[2])*c[3])*d[0]+(a[3]*c[0]*c[1]-c[0]*c[1]*c[3])*d[1])*PW2(d[2])+(3*b[3]*PW3(c[0])+PW2(c[0])*c[1]*d[2]-(3*a[3]*PW2(c[0])-PW3(c[1])+3*c[0]*c[1]*c[2]-3*PW2(c[0])*c[3])*d[0]-(c[0]*PW2(c[1])-2*PW2(c[0])*c[2])*d[1])*PW2(d[3])-(3*a[3]*PW2(b[3])*PW2(c[0])-PW2(b[3])*PW3(c[1])+3*PW2(b[3])*c[0]*c[1]*c[2]-3*PW2(b[3])*PW2(c[0])*c[3])*d[0]-(PW2(b[3])*c[0]*PW2(c[1])-2*PW2(b[3])*PW2(c[0])*c[2]+(PW2(a[3])*c[2]-2*a[3]*c[2]*c[3]+c[2]*PW2(c[3]))*PW2(d[0])+(2*a[3]*b[3]*PW2(c[1])+a[3]*b[3]*c[0]*c[2]+b[3]*c[1]*PW2(c[2])-(2*b[3]*PW2(c[1])+b[3]*c[0]*c[2])*c[3])*d[0])*d[1]+(PW2(b[3])*PW2(c[0])*c[1]-(2*PW2(a[3])*c[1]+a[3]*PW2(c[2])+2*c[1]*PW2(c[3])-(4*a[3]*c[1]+PW2(c[2]))*c[3])*PW2(d[0])-(a[3]*c[0]*c[2]-c[0]*c[2]*c[3])*PW2(d[1])+(a[3]*b[3]*c[0]*c[1]+b[3]*PW2(c[1])*c[2]-2*b[3]*c[0]*PW2(c[2])-b[3]*c[0]*c[1]*c[3])*d[0]-(3*a[3]*b[3]*PW2(c[0])+b[3]*c[0]*c[1]*c[2]-3*b[3]*PW2(c[0])*c[3]-(3*PW2(a[3])*c[0]+a[3]*c[1]*c[2]+3*c[0]*PW2(c[3])-(6*a[3]*c[0]+c[1]*c[2])*c[3])*d[0])*d[1])*d[2]-(3*PW2(b[3])*PW3(c[0])+PW2(c[0])*c[2]*PW2(d[2])+(3*PW2(a[3])*c[0]+3*a[3]*c[1]*c[2]+PW3(c[2])+3*c[0]*PW2(c[3])-3*(2*a[3]*c[0]+c[1]*c[2])*c[3])*PW2(d[0])+(2*a[3]*c[0]*c[1]+c[0]*PW2(c[2])-2*c[0]*c[1]*c[3])*PW2(d[1])-2*(3*a[3]*b[3]*PW2(c[0])-b[3]*PW3(c[1])+3*b[3]*c[0]*c[1]*c[2]-3*b[3]*PW2(c[0])*c[3])*d[0]-(2*b[3]*c[0]*PW2(c[1])-4*b[3]*PW2(c[0])*c[2]+(2*a[3]*PW2(c[1])+a[3]*c[0]*c[2]+c[1]*PW2(c[2])-(2*PW2(c[1])+c[0]*c[2])*c[3])*d[0])*d[1]+(2*b[3]*PW2(c[0])*c[1]+(a[3]*c[0]*c[1]+PW2(c[1])*c[2]-2*c[0]*PW2(c[2])-c[0]*c[1]*c[3])*d[0]-(3*a[3]*PW2(c[0])+c[0]*c[1]*c[2]-3*PW2(c[0])*c[3])*d[1])*d[2])*d[3];
}
// 関数値を求める
double p_(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
double x) // IN x
{
return ((((((((ca[0]*x+ca[1])*x+ca[2])*x+ca[3])*x+ca[4])*x+ca[5])*x+ca[6])*x+ca[7])*x+ca[8])*x+ca[9];
}
// 微分値を求める
double pd(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
double x) // IN x
{
return (((((((9*ca[0]*x+8*ca[1])*x+7*ca[2])*x+6*ca[3])*x+5*ca[4])*x+4*ca[5])*x+3*ca[6])*x+2*ca[7])*x+ca[8];
}
// 係数列の符号変化の回数を求める
int nSignVariation(
double *a, // IN 係数列
int n) // IN 係数列のサイズ-1
{
int rv=0;
int sign=0;
for(int i=0;i<=n;i++){
if((sign==1&&*a<0)||(sign==-1&&*a>0))
++rv;
if(*a>0)
sign=1;
else if(*a<0)
sign=-1;
++a;
}
return rv;
}
// Budanの定理のp(x+1)の係数を求める
void coefBudan(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
double *cb) // OUT p(x+1)の係数列 cb[0]が9次項の係数
{
cb[0]=ca[0];
cb[1]=9*ca[0]+ca[1];
cb[2]=36*ca[0]+8*ca[1]+ca[2];
cb[3]=84*ca[0]+28*ca[1]+7*ca[2]+ca[3];
cb[4]=126*ca[0]+56*ca[1]+21*ca[2]+6*ca[3]+ca[4];
cb[5]=126*ca[0]+70*ca[1]+35*ca[2]+15*ca[3]+5*ca[4]+ca[5];
cb[6]=84*ca[0]+56*ca[1]+35*ca[2]+20*ca[3]+10*ca[4]+4*ca[5]+ca[6];
cb[7]=36*ca[0]+28*ca[1]+21*ca[2]+15*ca[3]+10*ca[4]+6*ca[5]+3*ca[6]+ca[7];
cb[8]=9*ca[0]+8*ca[1]+7*ca[2]+6*ca[3]+5*ca[4]+4*ca[5]+3*ca[6]+2*ca[7]+ca[8];
cb[9]=ca[0]+ca[1]+ca[2]+ca[3]+ca[4]+ca[5]+ca[6]+ca[7]+ca[8]+ca[9];
}
// VAG法の係数を求める
void coefVAG(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
double a, // IN 区間の端点
double b,
double *cv) // OUT VAG係数列 cv[0]が9次項の係数
{
cv[0]=((((((((ca[0]*b+ca[1])*b+ca[2])*b+ca[3])*b+ca[4])*b+ca[5])*b+ca[6])*b+ca[7])*b+ca[8])*b+ca[9];
cv[1]=((((((((9*a*ca[0]+ca[1])*b+8*a*ca[1]+2*ca[2])*b+7*a*ca[2]+3*ca[3])*b+6*a*ca[3]+4*ca[4])*b+5*a*ca[4]+5*ca[5])*b+4*a*ca[5]+6*ca[6])*b+3*a*ca[6]+7*ca[7])*b+2*a*ca[7]+8*ca[8])*b+a*ca[8]+9*ca[9];
cv[2]=((((((((36*a*ca[0]+8*ca[1])*a+ca[2])*b+(28*a*ca[1]+14*ca[2])*a+3*ca[3])*b+(21*a*ca[2]+18*ca[3])*a+6*ca[4])*b+(15*a*ca[3]+20*ca[4])*a+10*ca[5])*b+(10*a*ca[4]+20*ca[5])*a+15*ca[6])*b+(6*a*ca[5]+18*ca[6])*a+21*ca[7])*b+(3*a*ca[6]+14*ca[7])*a+28*ca[8])*b+(a*ca[7]+8*ca[8])*a+36*ca[9];
cv[3]=((((((((84*a*ca[0]+28*ca[1])*a+7*ca[2])*a+ca[3])*b+((56*a*ca[1]+42*ca[2])*a+18*ca[3])*a+4*ca[4])*b+((35*a*ca[2]+45*ca[3])*a+30*ca[4])*a+10*ca[5])*b+((20*a*ca[3]+40*ca[4])*a+40*ca[5])*a+20*ca[6])*b+((10*a*ca[4]+30*ca[5])*a+45*ca[6])*a+35*ca[7])*b+((4*a*ca[5]+18*ca[6])*a+42*ca[7])*a+56*ca[8])*b+((a*ca[6]+7*ca[7])*a+28*ca[8])*a+84*ca[9];
cv[4]=((((((((126*a*ca[0]+56*ca[1])*a+21*ca[2])*a+6*ca[3])*a+ca[4])*b+(((70*a*ca[1]+70*ca[2])*a+45*ca[3])*a+20*ca[4])*a+5*ca[5])*b+(((35*a*ca[2]+60*ca[3])*a+60*ca[4])*a+40*ca[5])*a+15*ca[6])*b+(((15*a*ca[3]+40*ca[4])*a+60*ca[5])*a+60*ca[6])*a+35*ca[7])*b+(((5*a*ca[4]+20*ca[5])*a+45*ca[6])*a+70*ca[7])*a+70*ca[8])*b+(((a*ca[5]+6*ca[6])*a+21*ca[7])*a+56*ca[8])*a+126*ca[9];
cv[5]=((((((((126*ca[0]*b+56*ca[1])*b+21*ca[2])*b+6*ca[3])*b+ca[4])*a+(((70*ca[1]*b+70*ca[2])*b+45*ca[3])*b+20*ca[4])*b+5*ca[5])*a+(((35*ca[2]*b+60*ca[3])*b+60*ca[4])*b+40*ca[5])*b+15*ca[6])*a+(((15*ca[3]*b+40*ca[4])*b+60*ca[5])*b+60*ca[6])*b+35*ca[7])*a+(((5*ca[4]*b+20*ca[5])*b+45*ca[6])*b+70*ca[7])*b+70*ca[8])*a+(((ca[5]*b+6*ca[6])*b+21*ca[7])*b+56*ca[8])*b+126*ca[9];
cv[6]=((((((((84*ca[0]*b+28*ca[1])*b+7*ca[2])*b+ca[3])*a+((56*ca[1]*b+42*ca[2])*b+18*ca[3])*b+4*ca[4])*a+((35*ca[2]*b+45*ca[3])*b+30*ca[4])*b+10*ca[5])*a+((20*ca[3]*b+40*ca[4])*b+40*ca[5])*b+20*ca[6])*a+((10*ca[4]*b+30*ca[5])*b+45*ca[6])*b+35*ca[7])*a+((4*ca[5]*b+18*ca[6])*b+42*ca[7])*b+56*ca[8])*a+((ca[6]*b+7*ca[7])*b+28*ca[8])*b+84*ca[9];
cv[7]=((((((((36*ca[0]*b+8*ca[1])*b+ca[2])*a+(28*ca[1]*b+14*ca[2])*b+3*ca[3])*a+(21*ca[2]*b+18*ca[3])*b+6*ca[4])*a+(15*ca[3]*b+20*ca[4])*b+10*ca[5])*a+(10*ca[4]*b+20*ca[5])*b+15*ca[6])*a+(6*ca[5]*b+18*ca[6])*b+21*ca[7])*a+(3*ca[6]*b+14*ca[7])*b+28*ca[8])*a+(ca[7]*b+8*ca[8])*b+36*ca[9];
cv[8]=((((((((9*ca[0]*b+ca[1])*a+8*ca[1]*b+2*ca[2])*a+7*ca[2]*b+3*ca[3])*a+6*ca[3]*b+4*ca[4])*a+5*ca[4]*b+5*ca[5])*a+4*ca[5]*b+6*ca[6])*a+3*ca[6]*b+7*ca[7])*a+2*ca[7]*b+8*ca[8])*a+ca[8]*b+9*ca[9];
cv[9]=((((((((ca[0]*a+ca[1])*a+ca[2])*a+ca[3])*a+ca[4])*a+ca[5])*a+ca[6])*a+ca[7])*a+ca[8])*a+ca[9];
}
// Budanの定理による実根の有無検定
int vBudan( // RETURN p(x)とp(x+1)の係数の符号変化の数の差
double *ca) // IN 関数の係数列 ca[0]が9次項の係数
{
double cb[10];
coefBudan(ca,cb);
return nSignVariation(ca,9)-nSignVariation(cb,9);
}
// VAG法により実根が1個含まれる区間を求める
void vVAG(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
Interval &iv, // IN 対象の区間
vector<Interval> &ov) // OUT 実根が1個含まれる区間
{
double cv[10];
coefVAG(ca,iv.a,iv.b,cv);
int var=nSignVariation(cv,9);
if(var==0){
return;
}else if(var==1){
Interval nv;
nv.a=iv.a;
nv.b=iv.b;
nv.pa=p_(ca,iv.a);
nv.pb=p_(ca,iv.b);
ov.push_back(nv);
return;
}
double m=(iv.a+iv.b)/2;
double pm=p_(ca,m);
{
Interval nv;
nv.a=iv.a;
nv.b=m;
nv.pa=iv.pa;
nv.pb=pm;
vVAG(ca,nv,ov);
}
if(pm==0.0){
Interval nv;
nv.a=nv.b=m;
nv.pa=nv.pb=0.0;
ov.push_back(nv);
}
{
Interval nv;
nv.a=m;
nv.b=iv.b;
nv.pa=pm;
nv.pb=iv.pb;
vVAG(ca,nv,ov);
}
}
// 二分法により実根が1個含まれる区間を1/2に縮小する
void vBisection(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
Interval &v) // IN/OUT 対象の区間
{
if(v.a<v.b){
double m=(v.a+v.b)/2;
double pm=p_(ca,m);
if(pm==0.0){
v.a=v.b=m;
v.pa=v.pb=0.0;
return;
}else if(((v.pa>0||(v.pa==0.0&&pd(ca,v.a)>0.0))&&pm<0)||
((v.pa<0||(v.pa==0.0&&pd(ca,v.a)<0.0))&&pm>0)){
v.b=m;
v.pb=pm;
}else{
v.a=m;
v.pa=pm;
}
}
return;
}
// Ridder's法により9次関数の実根を求める
// 出典:Kiusalaas, Jaan (2010). Numerical Methods in Engineering with Python (2nd ed.). Cambridge University Press. pp. 147–148. ISBN 978-0-521-19132-6
double ridder( // RETURN 根の近似値
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
Interval &v, // IN 対象の区間
double tol) // IN 収束判定しきい値
{
double a=v.a;
double b=v.b;
double fa=v.pa;
double fb=v.pb;
if(fa==0.0)
return a;
if(fb==0.0)
return b;
if(fa*fb>0.0){
return nan(""); // root is not bracketed
}
double xOld;
for(int i=0;i<30;i++){
// Compute the improved root x from Ridder's formula
double c=0.5*(a+b);
double fc=p_(ca,c);
double s=sqrt(fc*fc-fa*fb);
if(s==0)
return nan("");
double dx=(c-a)*fc/s;
if(fa-fb<0.0)
dx=-dx;
double x=c+dx;
double fx=p_(ca,x);
// Test for convergence
if(i>0&&abs(x-xOld)<tol)
return x;
xOld=x;
// Re-bracket the root as tightly as possible
if(fc*fx>0.0){
if(fa*fx<0.0){
b=x;
fb=fx;
}else{
a=x;
fa=fx;
}
}else{
a=c;
b=x;
fa=fc;
fb=fx;
}
}
return nan(""); // Too many iterations
}
// 9次関数の区間[0,1}の実根を求める
void vRoots(
double *ca, // IN 関数の係数列 ca[0]が9次項の係数
vector<double> &rt) // OUT 実根
{
rt.clear();
Interval iv; // 根を求める区間
iv.a=0.0;
iv.b=1.0;
iv.pa=p_(ca,0.0);
iv.pb=p_(ca,1.0);
vector<Interval> rv; // 1つの根が含まれる区間
rv.reserve(9);
if(iv.pa==0.0){
// 始点の関数値が0なので、0を根とする
Interval nv;
nv.a=nv.b=0.0;
nv.pa=nv.pb=iv.pa;
rv.push_back(nv);
}
// {0,1}の実根を求める
int nb=vBudan(ca); // Budanの定理による実根の有無検定
if(nb==1){
// {0,1}に1個の実根がある
rv.push_back(iv);
}else if(nb>=2){
// {0,1}に1個以上の実根がある
vVAG(ca,iv,rv);
}
if(rv.size()==0){
// 交点なし、終了
return;
}
// 二分法により実根が1個含まれる区間を1/8に縮小する
for(Interval& v:rv){
vBisection(ca,v);
vBisection(ca,v);
vBisection(ca,v);
}
// Ridder's法により実根を求める
for(Interval& v:rv){
if(v.a==v.b){
rt.push_back(v.pa);
}else{
double r=ridder(ca,v,1e-6);
if(!isnan(r)){
rt.push_back(r);
}
}
}
}
// 3次ベジェ曲線の交点座標を求める
bool vBezierIntersection( // RETURN true:正常
QList<QPointF> &cp0, // IN 3次ベジェ曲線#0 制御点
QList<QPointF> &cp1, // IN 3次ベジェ曲線#1 制御点
QList<QPointF> &op) // OUT 交点座標
{
op.clear();
if(cp0.size()!=4||cp1.size()!=4)
return false;
// ベジェ曲線の係数を求める
double a[4],b[4],c[4],d[4];
coefBezier(cp0,a,b);
coefBezier(cp1,c,d);
// 交点の陰伏方程式F0(u),F1(t)の係数を求める
double cf0[10],cf1[10];
coefImp0(a,b,c,d,cf0);
coefImp1(a,b,c,d,cf1);
vector<double> rt0,rt1; // 根
rt0.reserve(9);
rt1.reserve(9);
// F0(u),F1(t)の根を求める
vRoots(cf0,rt0);
vRoots(cf1,rt1);
QList<QPointF> ip0,ip1; // 交点候補
for(double u:rt0)
ip0<<pointBezier(c,d,u);
for(double t:rt1)
ip1<<pointBezier(a,b,t);
foreach(QPointF p0,ip0){
foreach(QPointF p1,ip1){
double dx=p1.x()-p0.x();
double dy=p1.y()-p0.y();
if(sqrt(PW2(dx)+PW2(dy))<=0.0001){
op<<p0;
}
}
}
return true;
}
Qtサンプルアプリ
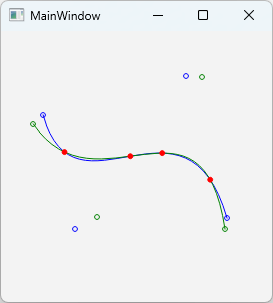
動作確認がてら、Qt上で動作するサンプルアプリを仕立ててみました。
起動すると前回の例①(ただし座標値10倍、上下反転)が表示されます。
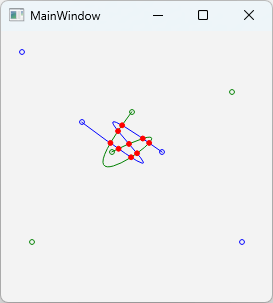
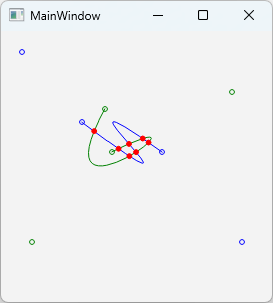
制御点をドラッグして移動すると曲線が更新され、交点が再計算されます。
#ifndef MAINWINDOW_H
#define MAINWINDOW_H
#include <QMainWindow>
#include <QMouseEvent>
#include <QGraphicsScene>
#include <QGraphicsItem>
#include "scene.h"
QT_BEGIN_NAMESPACE
namespace Ui { class MainWindow; }
QT_END_NAMESPACE
class MainWindow : public QMainWindow
{
Q_OBJECT
public:
MainWindow(QWidget *parent = nullptr);
~MainWindow();
private slots:
void mouseMove(QGraphicsSceneMouseEvent *mouseEvent);
void mousePress(QGraphicsSceneMouseEvent *mouseEvent);
private:
Scene scene;
QGraphicsEllipseItem *rc0[4];
QGraphicsEllipseItem *rc1[4];
QGraphicsPathItem *ci0;
QGraphicsPathItem *ci1;
QList<QGraphicsEllipseItem *> ri;
QList<QPointF> cp0;
QList<QPointF> cp1;
int scp;
private:
Ui::MainWindow *ui;
};
#endif // MAINWINDOW_H
#include "mainwindow.h"
#include "ui_mainwindow.h"
bool vBezierIntersection(
QList<QPointF> &cp0, // IN 3次ベジェ曲線#0 制御点
QList<QPointF> &cp1, // IN 3次ベジェ曲線#1 制御点
QList<QPointF> &op); // OUT 交点座標
MainWindow::MainWindow(QWidget *parent)
: QMainWindow(parent)
, ui(new Ui::MainWindow)
{
ui->setupUi(this);
scene.setSceneRect(0,0,ui->graphicsView->width()-2,ui->graphicsView->height()-2);
ui->graphicsView->setScene(&scene);
ui->graphicsView->setRenderHint(QPainter::Antialiasing);
// 例①の10倍
cp0<<QPointF(70,80);
cp0<<QPointF(230,200);
cp0<<QPointF(10,10);
cp0<<QPointF(150,110);
cp1<<QPointF(100,110);
cp1<<QPointF(220,50);
cp1<<QPointF(20,200);
cp1<<QPointF(120,70);
for(int i=0;i<4;i++){
rc0[i]=scene.addEllipse(cp0[i].x()-2.5,cp0[i].y()-2.5,5,5,QPen(Qt::blue));
rc1[i]=scene.addEllipse(cp1[i].x()-2.5,cp1[i].y()-2.5,5,5,QPen(Qt::darkGreen));
}
{
QPainterPath curve(cp0[0]);
curve.cubicTo(cp0[1],cp0[2],cp0[3]);
ci0=scene.addPath(curve,QPen(QBrush(Qt::blue),1));
}
{
QPainterPath curve(cp1[0]);
curve.cubicTo(cp1[1],cp1[2],cp1[3]);
ci1=scene.addPath(curve,QPen(QBrush(Qt::darkGreen),1));
}
QList<QPointF> op;
vBezierIntersection(cp0,cp1,op);
foreach (QPointF p,op)
ri<<scene.addEllipse(p.x()-2.5,p.y()-2.5,5,5,QPen(Qt::red),QBrush(Qt::red));
scp=-1;
connect(&scene,SIGNAL(mouseMove(QGraphicsSceneMouseEvent*)),this,SLOT(mouseMove(QGraphicsSceneMouseEvent*)));
connect(&scene,SIGNAL(mousePress(QGraphicsSceneMouseEvent*)),this,SLOT(mousePress(QGraphicsSceneMouseEvent*)));
}
MainWindow::~MainWindow()
{
delete ui;
}
void MainWindow::mouseMove(QGraphicsSceneMouseEvent *mouseEvent)
{
if((mouseEvent->buttons()&Qt::LeftButton)&&scp>=0){
QPointF pos=mouseEvent->scenePos();
if(scp<=3){
cp0[scp]=pos;
rc0[scp]->setRect(pos.x()-2.5,pos.y()-2.5,5,5);
QPainterPath curve(cp0[0]);
curve.cubicTo(cp0[1],cp0[2],cp0[3]);
ci0->setPath(curve);
}else{
cp1[scp-4]=pos;
rc1[scp-4]->setRect(pos.x()-2.5,pos.y()-2.5,5,5);
QPainterPath curve(cp1[0]);
curve.cubicTo(cp1[1],cp1[2],cp1[3]);
ci1->setPath(curve);
}
foreach(QGraphicsEllipseItem *gi,ri){
scene.removeItem(gi);
delete gi;
}
ri.clear();
QList<QPointF> op;
vBezierIntersection(cp0,cp1,op);
foreach(QPointF p,op)
ri<<scene.addEllipse(p.x()-2.5,p.y()-2.5,5,5,QPen(Qt::red),QBrush(Qt::red));
}
}
void MainWindow::mousePress(QGraphicsSceneMouseEvent *mouseEvent)
{
if(mouseEvent->buttons() & Qt::LeftButton){
QPointF pos = mouseEvent->scenePos();
scp=-1;
for(int i=0;i<4;i++){
if(QLineF(pos,rc0[i]->rect().center()).length()<=5)
scp=i;
}
for(int i=0;i<4;i++){
if(QLineF(pos,rc1[i]->rect().center()).length()<=5)
scp=i+4;
}
}
}
#ifndef SCENE_H
#define SCENE_H
#include <QObject>
#include <QGraphicsScene>
#include <QGraphicsSceneMouseEvent>
class Scene : public QGraphicsScene
{
Q_OBJECT
public:
explicit Scene(QObject *parent = nullptr);
signals:
void mouseMove(QGraphicsSceneMouseEvent *mouseEvent);
void mousePress(QGraphicsSceneMouseEvent *mouseEvent);
protected:
virtual void mouseMoveEvent(QGraphicsSceneMouseEvent *mouseEvent) override;
virtual void mousePressEvent(QGraphicsSceneMouseEvent *mouseEvent) override;
};
#endif // SCENE_H
#include "scene.h"
Scene::Scene(QObject *parent)
: QGraphicsScene{parent}
{
}
void Scene::mouseMoveEvent(QGraphicsSceneMouseEvent *mouseEvent)
{
emit mouseMove(mouseEvent);
}
void Scene::mousePressEvent(QGraphicsSceneMouseEvent *mouseEvent)
{
emit mousePress(mouseEvent);
}
uiは centralwidget に QGraphicsView graphicsView を置くだけです。サイズや位置は任意です。
関連記事