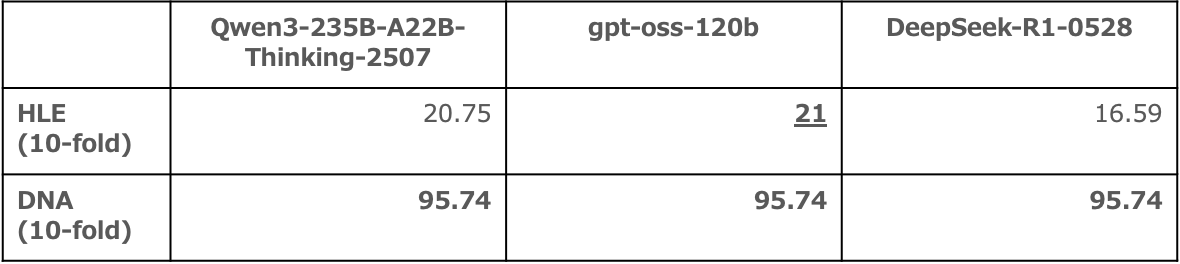この記事では、松尾研LLM開発コンペ2025における準優勝チームの取り組みを説明します。
松尾研LLM開発コンペ2025 について
このコンペは、既存の大規模言語モデル(LLM)に対して事後学習を行い推論モデル(reasoningモデル)の開発に取り組み、ベンチマークのスコアを競うコンペです。
ベンチマークとしては、最難関とされるHumanity’s Last Exam(HLE)と安全性評価のDo-Not-Answer(DNA)のふたつです。
専門家を超える推論性能とともに高水準の安全性を追求し、オープンモデルとして最高性能(SOTA)の達成を目指しました。
戦略と戦術
我々のチームが決勝戦で集中したことは、“数学のスコアを維持しながら、数学以外のカテゴリを底上げする”ことです(戦略)。
最先端モデルは数学特化でチューニングされており非常に強い一方、数学以外のカテゴリはのびしろがあると考えていました。
ただ、最先端モデルを学習したさいに数学スコアを維持するには高難度の問題が不可欠です。
というのも、低中難度の問題だと、それにオーバーフィットしてしまうかもしれないからです。
そこで、数学カテゴリでは高難度データセットを中心に構築することとしました(戦術)。
データセットの構築
高難度数学データセットとしては、数学オリンピックや大学レベルの難度のデータセットを選別しました。
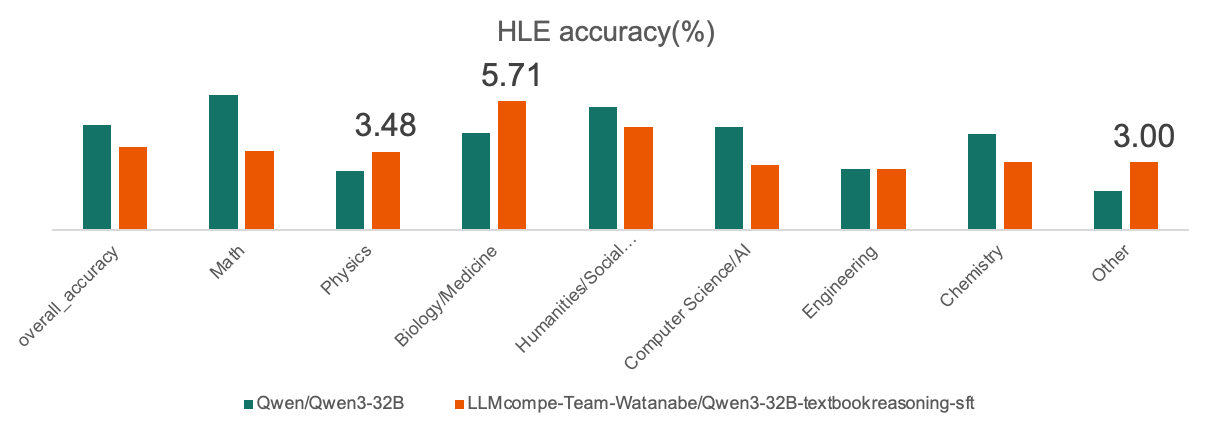
Qwen3-32B で実験したところ Omni-MathとHARDMathで数学スコアが向上したことから、これらのデータセットと同等の難度、つまりオリンピックあるいは大学レベルの何度を基準としました。
いっぽう、数学以外のカテゴリについては TextbookReasoning を採用しました。
これは、他チームでの実験において物理など3カテゴリでスコアが改善したため、数学以外の幅広いカテゴリで推論能力を補強できると判断したためです。
データセット全体のカテゴリ分布については、HLE と同じになるように調整しました。
具体的には、OlymMathをはじめ4つの数学データセットに対して TextbookReasoning をDown Sampling しました。
なお、OlymMath と Omni-Math にはクローズドモデルの出力が含まれていたため、
該当箇所を除去して学習に利用しました。
事後学習
事後学習のベースモデルには、Qwen3-235B-A22B-Thinking-2507 を選びました。
gpt-oss-120b と比較するとHLEのスコアは僅かに下回っていましたが、
予選での学習結果の事例が多く 追加学習の効果を予測しやすい点を有利と判断しました。
事後学習はフルパラメーターの SFT を採用しました。
というのも、数学特化 のSFT により学習済みモデルのスコアを向上させた Light-R1 の事例があったからです。
同様の設定にあたる今回のコンペについても数学の精度向上の確度が高いと判断しました。
なお、 RL 系の学習についても試したかったものの、時間とノードが足りず実施できませんでした。
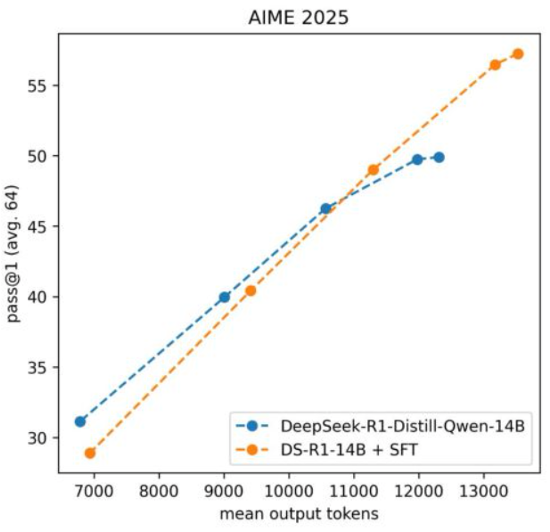
また、モデルの推論時には max_completion_tokens を最大化しています。
というのも、高難度の数学問題において出力長と正答率に正の相関があるというAIMO2コンペの事例があったからです。
しかも、max_completion_tokens が小さいと推論時に回答が欠損する現象を観測していたので、最大化によってそれを防ぐ目的もありました。
なお、モデル評価では、比較の公平性を保つため、すべてのモデルで同じ max_completion_tokens の値を用いて推論しています。
モデルの評価
最終的に我々のチームの提出候補となったモデルは、8 モデルでした。
そのうち提出モデルに選んだのは、overall と数学カテゴリの両方でベースを上回ったモデルです。
ちなみに、我々のチームでは HLE の全件評価によってモデルの優劣を判断していたため提出候補モデルの数は比較的少ないと思います。
実際、締め切り時刻までに評価が完了しなかったモデルもありました。
提出モデルのスコアとしては、overallでの正答率が18.91%となり、ベースモデルを0.84ポイント上回っていました。
カテゴリ別に見ても数学などの7カテゴリでベースモデルを上回るスコアになっていました。
しかしながら、結果発表時のスコアは正答率18.49%となり、ベースモデルを0.88ポイント下回る最終結果となってしまいました。
結果発表時とスコアが乖離してしまった原因としては、HLE の pass-1 評価におけるばらつきだと考えています。
HLE の公式実装では正答率とともに信頼区間を算出しています。
提出モデルとベースモデルの信頼区間を見ると、両者が重なっており、統計的に有意な差はないと言えます。
つまり、スコア差よりもばらつきの方が大きいので、スコア差が性能差であるとは判断できないということです。
ちなみに、LLMの性能評価において統計的な比較を実施していない事例は少なくないようです。
該当論文のうち16%しか統計的な比較をしていないという報告も最近ありました。
定量評価に加えて、数学問題におけるベースモデルと提出モデルの定性評価も行いました。
両モデルの回答で正答/誤答が分かれた問題を比較すると、
推論過程には類似点があり・どちらも推論過程に誤りを含むことが分かりました。
問題としては3次方程式の値が平方数になる整数xを求める問題でした。
どちらの回答にもどちらも誤った論理展開があり、誤った推論が正答を導くのを妨げれば誤答となり・そうでなければ正答となっていました。
このことから、提出モデル・ベースモデルのどちらもその学習時に推論の誤りを十分に抑制できていない可能性があり、それがスコア低下につながっている恐れがあると考えています。
事後学習とモデル評価を振り返ってみて
最先端モデルの数学スコアをさらに向上させるには、高難度の数学データセットが不可欠だと感じました。
数学のスコアの更なる向上を目指すには、合成などデータの水増しにより高難度問題を新たに作り出すアプローチが必要だと考えています。
また、提出モデル・ベースモデルのどちらもが推論過程に誤りを含んでいて、それが正答誤答に影響している事例がありました。
推論過程における論理の飛躍などを検出する仕組みがあれば、強化学習によりさらに数学スコアを改善できると考えています。
まとめ
- 高難度数学データセットの収集に注力し、ベースモデルを上回るスコアを目指した
- 同データセットを含むSFTを行ったが、数学でのスコアをキープし・overallでベースモデルを上回ったとまでは言い切れない結果であった
モデルとデータセットの公開
事後学習に用いたデータセットと学習済みの提出モデルはどちらも huggingface にて公開しています:
- weblab-llm-competition-2025-bridge/team-pont-neuf-sft-dataset
- weblab-llm-competition-2025-bridge/team-pont-neuf-Qwen3-235B-A22B-Thinking-sft
もしフィードバックなどがあれば、ぜひいただけるとうれしいです!
謝辞
本プロジェクトは、国立研究開発法人新エネルギー・産業技術総合開発機構(NEDO)の「日本語版医療特化型LLMの社会実装に向けた安全性検証・実証」における基盤モデルの開発プロジェクトの一環として行われます。