0. はじめに
DeepLearningを使用した時系列/自然言語処理に関して調べたことをシェアしていく記事の第1弾です。第1回はRNN(Recurrent neural network)を扱います。
RNNの日本語記事はかなりありましたが、LSTMではなくRNNを使用した「sin波予測」以外のサンプルが少なかったり(というかほぼ無かった)Kerasを使用したRNN記事と比べて圧倒的にPyTorchで書かれた記事が少ないと感じたので、私なりに初心者でもわかるような直感的な表現を使いつつこの記事ではまとめていこうと思います。
RNNは今や古いので誰にも使われていませんが、いろんな分野の基礎になっているので理解しておくことは重要だと考えています。
例)テキスト解析、感情分析、文章翻訳、チャットボット、動画分析・・・etc
なお、本記事では自然言語ではなく「時系列処理」に関してRNNを適応した例を記載します。
1. RNNって何?
RNNは「時間方向」につながりを持たせられるニューラルネットである。
では時間方向って何?ということだが、まず通常のニューラルネットは下図のように複数の入力に対して中間層で特徴量を抽出して何かしらの出力を得る仕組みである。

しかし、時間や並びの順番に重要な意味を持つデータ**(これをシーケンシャルデータと呼ぶ)**に関しては通常のニューラルネットでは扱えないのである。
※1の次は2で、その次は3・・みたいな順番をニューラルネットでは学習できない
そこでRNN(再帰型ニューラルネットワーク)が考えられた。
ではRNNではどうやってシーケンシャルデータを学習するか?というと、各時刻で学習した特徴量を次の時刻の入力データとしても使うことで、前の時刻の情報を維持しながら学習するのである。
下図はイメージ図だが、時刻tのタイミングの入力データをRNNへ入れる時に時刻t-1の特徴量も一緒に入力させることで、t-1までに得た特徴も疑似的に加味させることができる。

ちなみに、上図のRNN_cellの中身は以下を足し合わせたものをtanhの活性化関数に通したものになっている。
①時刻tの入力$x_t$に重み$W_x$をかけたもの
②時刻t-1の隠れ層$h_{t-1}$に重み$W_h$をかけたもの
③x、hそれぞれのバイアス($b$) ※Pytorchではxとhでバイアスが分かれているが教科書的には1個
時刻tにおけるRNNの式:
h_{t} =tanh (W_{x}x_{t}+b_{x}+W_{h}h_{t-1}+b_{h})
なお、上図を見るとRNN_cellの出力が「上方向への出力と次のRNN_cellへの入力」と2分岐していることもわかるが、この2個は用途が違うだけで全く同じ出力である。
その他「RNNの逆伝番の仕組み(BPTT(backpropagation through time)」や「ステートフル」等の知識も知っておいたほうがいいが、この記事では複雑になりすぎるので割愛する。本記事を読み終わった後に別の方の記事や書籍を確認してみていただきたいです。
2. RNNの実装と予測(Pytorch)
2-1. データの確認とRNNへの入力イメージ
今回はairpasengerを題材にPyTorchを使って実装したので以下で解説していく。
なおライブラリのインポートには触れないので、必要に応じてpipコマンドで入れるようにしてください。
# 各種のインポート
import torch
from torch import nn,optim
from torch.utils.data import DataLoader, TensorDataset, Dataset
from torchvision import transforms
from torchinfo import summary #torchinfoはニューラルネットの中身を見れるのでおすすめ
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
import os
import random
# 乱数固定用の処理
seed = 10
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
# データをPandasで読み込み
df = pd.read_csv("AirPassengers.csv")
# データを3行だけ表示
df.head(3)
| |Month |#Passengers |
|---|---|---|---|---|
|0 |1949-01 |112 |
|1 |1949-02 |118 |
|2 |1949-03 |132 |
AirPassengersはこのように月別にどれくらいの乗客が乗ったか?を示すデータなことがわかる。
# Monthカラムは解析に不要なので排除
df = df.iloc[:,1].values
# 乗客数の1次元データとする
df = df.reshape(-1,1)
df = df.astype("float32")
# ニューラルネットの入力データは0~1へ正規化する必要があるので乗客数を正規化する
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range = (0, 1))
df_scaled = scaler.fit_transform(df)
# 正規化された乗客数の推移を図示して確認する
plt.plot(df_scaled)
plt.xlabel("time")
plt.ylabel("Number of Passenger")
plt.title("international airline passenger")
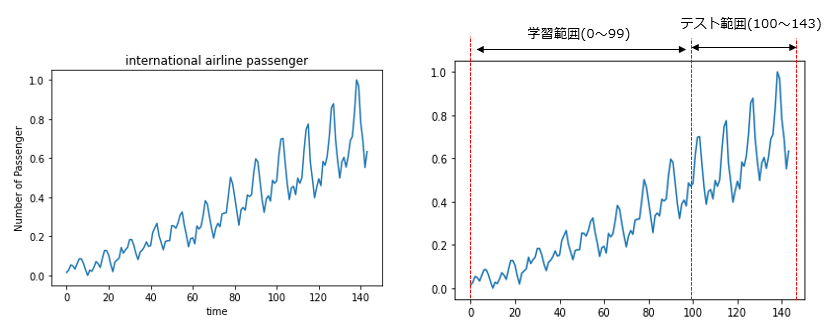
plt.show()
すると、左下の図が出力される。
これをRNNへの学習用とテスト用に分ける必要があるが、キリがいいので右下のように分けることにする。
ここでどうやってRNNへデータを渡して予測させるか?のイメージも載せておく。
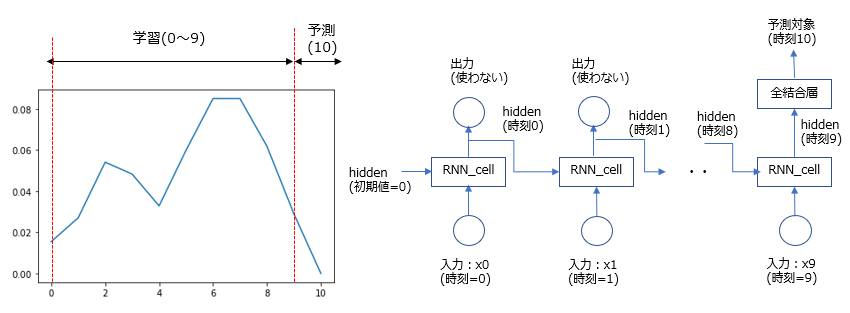
まずは上図の学習期間の中のt=0~10を抜き出したのが左下図になっている。なお今回は連続した10個のシーケンシャルデータを使って、11個目の時刻のデータを求めるような設定にしている。
※10個としているが、このシーケンシャルデータの数も一種のパラメータで何個としてもいい。
そしてt=0~9の10個のシーケンシャルデータをRNNへ入力し、t=10の値を予測させるRNNのイメージ図が右下図になる。
時刻t=9のRNN_cellには、時刻t=9の入力データ以外に時刻t=0から受け継がれてきた特徴量hiddenも加わって学習が行われる。
また今回RNNに求めさせたいのは、時刻t=10の数字(乗客数)なのでt=9の特徴量(hidden)の次元を1次元にする必要があり、時刻t=9の出力(hidden)を全結合層に入れることで次元削減をさせている。
そしてt=10の予測が終わったら、次は1個ずらして学習させる。
つまりt=1~10をRNNに入れて、t-11を予測・・のように徐々に学習させていくイメージである。
これを学習範囲の中で繰り返すのがRNNの時系列予測の基本的なやり方(考え方)になる。

2-2. 入力データの加工
先程述べたように学習とテストを分割する。
train_size = int(len(df_scaled) * 0.70) #学習サイズ(100個)
test_size = len(df_scaled) - train_size #全データから学習サイズを引けばテストサイズになる
train = df_scaled[0:train_size,:] #全データから学習の個所を抜粋
test = df_scaled[train_size:len(df_scaled),:] #全データからテストの個所を抜粋
print("train size: {}, test size: {} ".format(len(train), len(test)))
train size: 100, test size: 44
time_stemp = 10 #今回は10個のシーケンシャルデータを1固まりとするので10を設定
n_sample = train_size - time_stemp - 1 #学習予測サンプルはt=10~99なので89個
# シーケンシャルデータの固まり数、シーケンシャルデータの長さ、RNN_cellへの入力次元(1次元)に形を成形
input_data = np.zeros((n_sample, time_stemp, 1)) #シーケンシャルデータを格納する箱を用意(入力)
correct_input_data = np.zeros((n_sample, 1)) #シーケンシャルデータを格納する箱を用意(正解)
print(input_data.shape)
print(correct_input_data.shape)
(89, 10, 1) #10×1のシーケンシャルデータが89個ある
(89, 1)
今回の設定の場合、RNNへの入力として最低限10個のシーケンシャルデータが必要なので学習予測スタート地点が0ではないことに注意。
# 空のシーケンシャルデータを入れる箱に実際のデータを入れていく
"""
こんなイメージ?
0,1,2,・・・9 + 正解データt=10
1,2,・・・9,10 + 正解データt=11
2,・・・9,10,11 + 正解データt=12
"""
for i in range(n_sample):
input_data[i] = df_scaled[i:i+time_stemp].reshape(-1, 1)
correct_input_data[i] = df_scaled[i+time_stemp:i+time_stemp+1]
input_data = torch.tensor(input_data, dtype=torch.float) #Tensor化(入力)
correct_data = torch.tensor(correct_input_data, dtype=torch.float) #Tensor化(正解)
dataset = torch.utils.data.TensorDataset(input_data, correct_data) #データセット作成
train_loader = DataLoader(dataset, batch_size=4, shuffle=True) #データローダー作成
ここのバッチサイズは4としているが何でもいい。また、shuffle=Trueとしているが、Falseでもいい。
なお、ここに違和感を感じる方もいるかと思う(事実私は最初困惑した)が、実は先程説明を省いた「ステートフル」を理解するとより理解が深まる。簡単に言うと「t=0~9のRNN」と「t=1~10のRNN」自体の繋がりは学習対象である重みとバイアスの数字以外に実はなくて、互いに独立して学習させている。
つまり、hiddenは各シーケンシャルデータ毎に毎回0からスタートさせている為に学習順番をshuffleしても関係ないし、バッチサイズに関してもそこまで気にしなくていいのである。
2-3. RNNクラスの作成
class My_rnn_net(nn.Module):
def __init__(self, input_size, output_size, hidden_dim, n_layers):
super(My_rnn_net, self).__init__()
self.input_size = input_size #入力データ(x)
self.hidden_dim = hidden_dim #隠れ層データ(hidden)
self.n_layers = n_layers #RNNを「上方向に」何層重ねるか?の設定 ※横方向ではない
"""
PyTorchのRNNユニット。batch_first=Trueでバッチサイズを最初にくるように設定
また、先程示した図ではRNN_cellが複数あったがここではRNNが1個しかない。
つまりこの「nn.RNN」は複数のRNN_cellをひとまとめにしたものである。
※シーケンシャルデータと初期値のhiddenだけ入れてあげれば内部で勝手に計算してくれる
※出力部は各時刻毎に出力されるが、下で述べているように最後の時刻しか使用しない
"""
self.rnn = nn.RNN(input_size, hidden_dim, n_layers, batch_first=True)
self.fc = nn.Linear(hidden_dim, output_size) #全結合層でhiddenからの出力を1個にする
def forward(self, x):
#h0 = torch.zeros(self.n_layers, x.size(0), self.hidden_dim).to(device)
#y_rnn, h = self.rnn(x, h0)
y_rnn, h = self.rnn(x, None) #hidden部分はコメントアウトした↑2行と同じ意味になっている。
y = self.fc(y_rnn[:, -1, :]) #最後の時刻の出力だけを使用するので「-1」としている
return y
# RNNの設定
n_inputs = 1
n_outputs = 1
n_hidden = 64 #隠れ層(hidden)を64個に設定
n_layers = 1
net = My_rnn_net(n_inputs, n_outputs, n_hidden, n_layers) #RNNをインスタンス化
print(net) #作成したRNNの層を簡易表示
# おすすめのtorchinfoでさらに見やすく表示
batch_size = 4
summary(net, (batch_size, 10, 1))
My_rnn_net(
(rnn): RNN(1, 64, num_layers=2, batch_first=True)
(fc): Linear(in_features=64, out_features=1, bias=True)
)
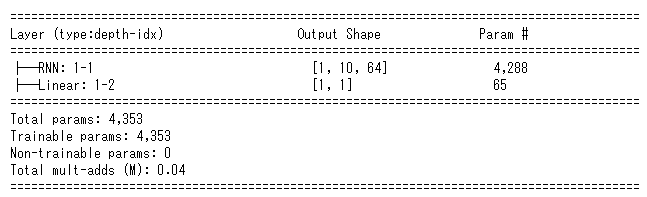
なお、torchinfoで示される上図のパラメータ数は上で示したRNNの数式に当てはめれば計算できる
$W_{x}x_{t}+b_{x}+W_{h}h_{t-1}+b_{h}$
⇒ 641 + 64 + 6464 + 64 = 4288 ※1次元のxを64層のhiddenに分けるのでxの重み数も64となる
2-4. RNNで学習
loss_fnc = nn.MSELoss() #損失関数はMSE
optimizer = optim.Adam(net.parameters(), lr=0.001) #オプティマイザはAdam
loss_record = [] #lossの推移記録用
device = torch.device("cuda:0" if torch.cuda. is_available() else "cpu") #デバイス(GPU or CPU)設定
epochs = 200 #エポック数
net.to(device) #モデルをGPU(CPU)へ
for i in range(epochs+1):
net.train() #学習モード
running_loss =0.0 #記録用loss初期化
for j, (x, t) in enumerate(train_loader): #データローダからバッチ毎に取り出す
x = x.to(device) #シーケンシャルデータをバッチサイズ分だけGPUへ
optimizer.zero_grad() #勾配を初期化
y = net(x) #RNNで予測
y = y.to('cpu') #予測結果をCPUに戻す
loss = loss_fnc(y, t) #MSEでloss計算
loss.backward() #逆伝番
optimizer.step() #勾配を更新
running_loss += loss.item() #バッチごとのlossを足していく
running_loss /= j+1 #lossを平均化
loss_record.append(running_loss) #記録用のlistにlossを加える
"""以下RNNの学習の経過を可視化するコード"""
if i%100 == 0: #今回は100エポック毎に学習がどう進んだか?を表示させる
print('Epoch:', i, 'Loss_Train:', running_loss)
input_train = list(input_data[0].reshape(-1)) #まず最初にt=0~9をlist化しておく
predicted_train_plot = [] #学習結果plot用のlist
net.eval() #予測モード
for k in range(n_sample): #学習させる点の数だけループ
x = torch.tensor(input_train[-time_stemp:]) #最新の10個のデータを取り出してTensor化
x = x.reshape(1, time_stemp, 1) #予測なので当然バッチサイズは1
x = x.to(device).float() #GPUへ
y = net(x) #予測
y = y.to('cpu') #結果をCPUへ戻す
"""
もっと綺麗なやり方あるかもですが、次のループで値をずらす為の部分。
t=0~9の予測が終了 ⇒ t=1~10で予測させたいのでt=10を追加する・・・を繰り返す
"""
if k <= n_sample-2:
input_train.append(input_data[k+1][9].item())
predicted_train_plot.append(y[0].item())
plt.plot(range(len(df_scaled)), df_scaled, label='Correct')
plt.plot(range(time_stemp, time_stemp+len(predicted_train_plot)), predicted_train_plot, label='Predicted')
plt.legend()
plt.show()
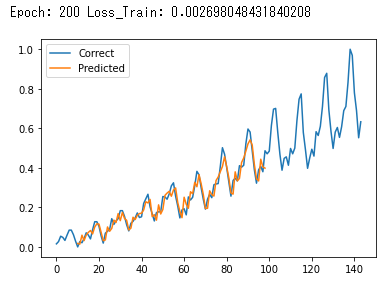
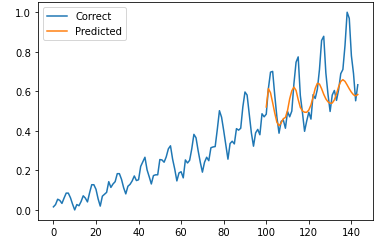
これを実行すると、最後の200Epoch目が以下のように出力されてて、うまく学習できていることがわかる。
※途中のEpoch出力は省略
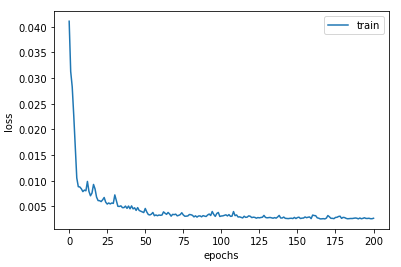
# 最後にlossの推移を確認
plt.plot(range(len(loss_record)), loss_record, label='train')
plt.legend()
plt.xlabel("epochs")
plt.ylabel("loss")
plt.show()
一応lossも確認しておくと、Epoch毎に下がっていることも確認できた。
2-5. RNNで未学習部分を予測
学習に使用してない部分を予測させる⇒t=100以降となるのでそのデータを準備する
つまり今回のテストではまず「t=90~99を使ってt=100を予測」から始まるのでt=90~133を先頭としたシーケンシャルデータを抜粋すればいい。
※正解データはt=143で終わるため、比較させる為に最後の入力はt=133~142となる
# 学習の時と同じ感じでまずは空のデータを作る
time_stemp = 10
n_sample_test = len(df_scaled) - train_size #テストサイズは学習で使ってない部分
test_data = np.zeros((n_sample_test, time_stemp, 1))
correct_test_data = np.zeros((n_sample_test, 1))
# t=90以降のデータを抜粋してシーケンシャルデータとして格納していく
start_test = 90
for i in range(n_sample_test):
test_data[i] = df_scaled[start_test+i : start_test+i+time_stemp].reshape(-1, 1)
correct_test_data[i] = df_scaled[start_test+i+time_stemp : start_test+i+time_stemp+1]
# 以下は学習と同じ要領
input_test = list(test_data[0].reshape(-1))
predicted_test_plot = []
net.eval()
for k in range(n_sample_test):
x = torch.tensor(input_test[-time_stemp:])
x = x.reshape(1, time_stemp, 1)
x = x.to(device).float()
y = net(x)
y = y.to('cpu')
if k <= n_sample_test-2:
input_test.append(test_data[k+1][9].item())
predicted_test_plot.append(y[0].item())
plt.plot(range(len(df_scaled)), df_scaled, label='Correct')
plt.plot(range(start_test+time_stemp, start_test+time_stemp+len(predicted_test_plot)), predicted_test_plot , label='Predicted')
plt.legend()
plt.show()
こんな感じで学習未使用データもきちんと予測できていそうである。
なお省略するが、元のスケールにはinverse_transformを使えば戻すことが出来る
3. おわりに
かなり長くなってしまったが、実は今回やっていないことがある。
本来の時系列予測でやりたいことは予測結果をさらに入力データとしてどんどん積み重ねてもいい具合の予測結果になっていることなのだが、結論から言うと今回のRNNでは全くうまくいかない。
下図が実際に予測期間において予測結果を次の時刻の入力データとして使用していった予測結果だが、うまく予測できていないことがわかる。
その理由は簡単で、予測結果を次の入力データに入れる・・を繰り返すと徐々に予測誤差の分だけずれていってしまう為である。なので私もあまり試せていないが、RNNは実際には使えないのでは?と考えている。
そこでGRUやLSTM等の次世代の技術が出てきたと思うので、次回はLSTMをやってみることにする。
それでは今回はここまで。
4.2021/6/30修正
テストの部分の記述が間違っていました。
正しくはx = torch.tensor(input_test[-time_stemp:])でした。修正いたします。
ついでに、、「おわりに」にも書きましたが、この手の時系列における真のテストは予測データを使用して次の予測をすることですので、悪しからず。