とりあえず
Pandasの勉強でCSVデータを取り込みデータ操作をやってみた。その結果として作成した多次元データを3次元で表現してみたい。ということで色々頑張ってみたのでその記事です。(くれぐれも・・・数学も機械学習もまだまだ初心者ですのであしからず・・・)
まずは
やりたいことは、N次元を3次元になんとかできれば、プロットできる。ってことで”次元削減”。
主成分分析やってみる。理論は結構ブログで書いている人もいるのでそれを読み漁ったみた。
そして実践。流石に主成分分析をpythonで組む自信は無いので、sklearnのPCAを使ってみる事に。
この記事を参考にしました。
print(target)
user_id date_x all p1 p2 ... p76 p77 p78 score flg
0 10404829 2017/6/28 33 35 36 ... 69.0 56.0 71.0 5819.0 2.0
1 10413677 2017/7/23 43 29 55 ... 53.0 50.0 58.0 4878.0 0.0
2 10377654 2017/5/15 32 32 37 ... 62.0 47.0 59.0 6290.0 0.0
3 10377655 2017/5/15 42 47 41 ... 44.0 59.0 46.0 4525.0 1.0
5 10479074 2017/12/4 42 47 40 ... 52.0 54.0 53.0 4643.0 1.0
6 10479075 2017/11/29 39 41 40 ... 46.0 40.0 46.0 4525.0 1.0
・・・
まずは意味が無いんじゃないかな?と思うものを除外してみる。
target.drop(columns=['all', 'score', 'date_x', 'date_y', 'flg', 'user_id'])
※ allとscoreはノリで除外しました。(date_x,date_y,flgは不要。user_idもindexで代用できる考え。)
必要なデータだけにして、sklearnのPCAで一気に3次元にしてみる。
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
pca.fit(target)
print("--- explained_variance_ratio_ ---")
print(pca.explained_variance_ratio_)
print("--- components ---")
print(pca.components_)
print("--- mean ---")
print(pca.mean_)
print("--- covariance ---")
print(pca.get_covariance())
結果は色々でてくるけどとりあえずこれだけは理解。
--- explained_variance_ratio_ ---
[0.38644673 0.13264016 0.10981307]
・・・
第1主成分は38%,第2主成分は13%,第3主成分は10%で説明できている。(ってことは、3次元に削ると60%しか精度が担保できていない?ってことかな?)
今回は、データの可視化が目的なので、ひとまずは・・・無視!
あとはその結果をDataFrame化してplotの元ネタにする。
transformしても、並び順は変わらない。っぽいのでindexで結合しても良さそう。
result = pca.transform(target)
# fit_transform 呼出しで両方が同時に実行可能。
result = pd.DataFrame(existing_2d)
result.index = target.index
result.columns = ['PC1', 'PC2', 'PC3']
3次元散布図を描画するためにmatplotlibを使う。
気にしたところは以下。
- グラフを大きめに。
- 3次元グラフに文字を印字(ラベル) ax.textちょー便利。
- DataFrameの要約統計量を使ってグラフの描画角を決める。
fig = plt.figure(num=None, figsize=(15, 15), dpi=150, facecolor='w', edgecolor='k') ←グラフをデカく
ax = fig.gca(projection='3d')
ax.plot(result['PC1'], result['PC2'], result['PC3'], marker="o", linestyle='None')
for i in result.index:
ax.text(result.iloc[i].PC1, result.iloc[i].PC2, result.iloc[i].PC3, i)
ax.set_xlim(result.describe().at['min', 'PC1']-10, result.describe().at['max', 'PC1']+10)
ax.set_ylim(result.describe().at['min', 'PC2']-10, result.describe().at['max', 'PC2']+10)
ax.set_zlim(result.describe().at['min', 'PC3']-10, result.describe().at['max', 'PC3']+10)
ax.set_xlabel('PC1')
ax.set_ylabel('PC2')
ax.set_zlabel('PC3')
plt.show()
<結果>

ひとまず目的達成!
はい!そうです!欲が出ました。
折角前回 k-meansやったので、このベクトルをクラスタリングしてみたくなりました。
やりたい事
N個のクラスタに分類して色を変える。
ここでふと疑問が・・・・ 主成分分析した結果の3次元ベクトルと元のN次元bベクトルでk-meansの結果は変わるのか?
まぁとりあえず両方やってみる事に。
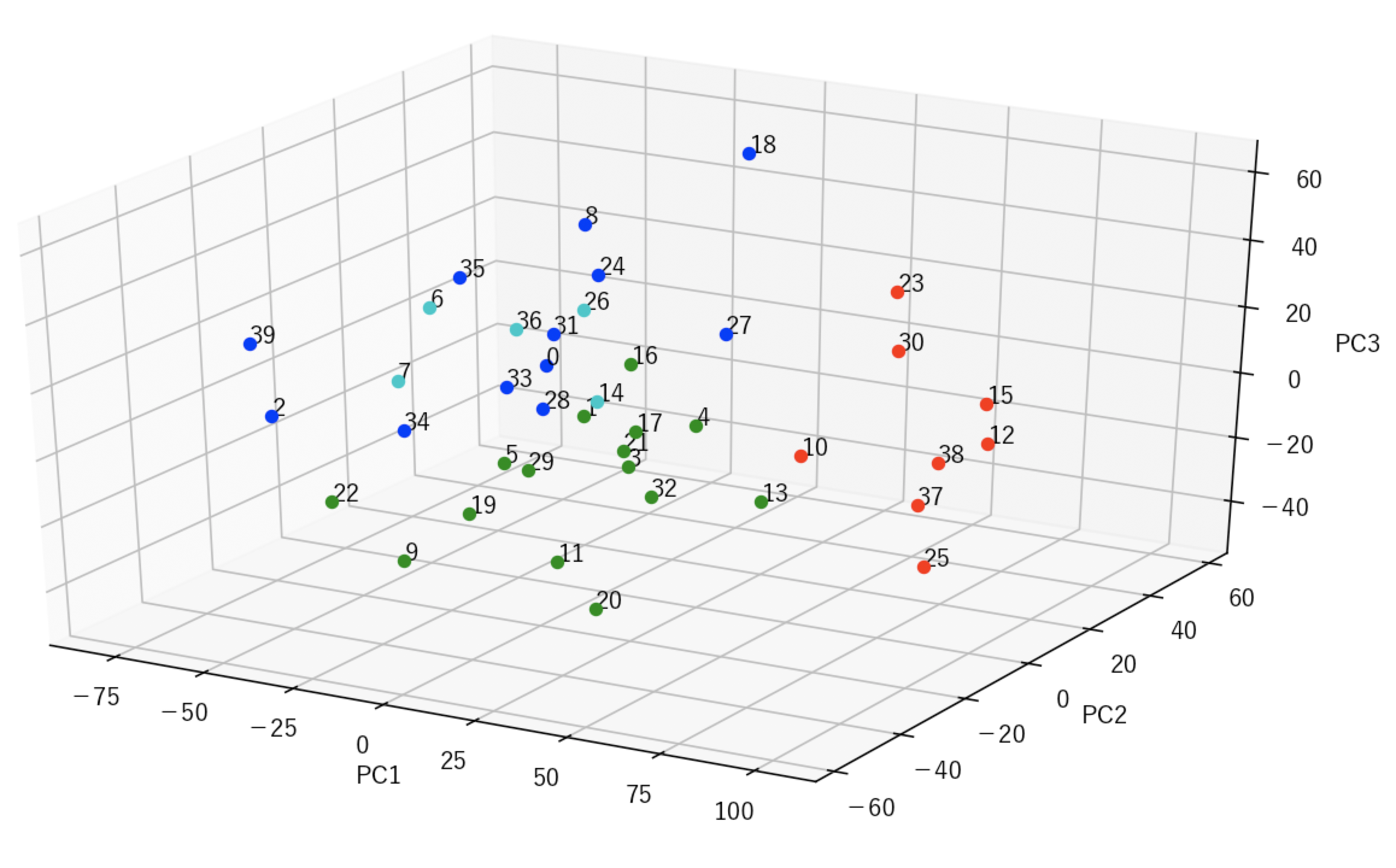
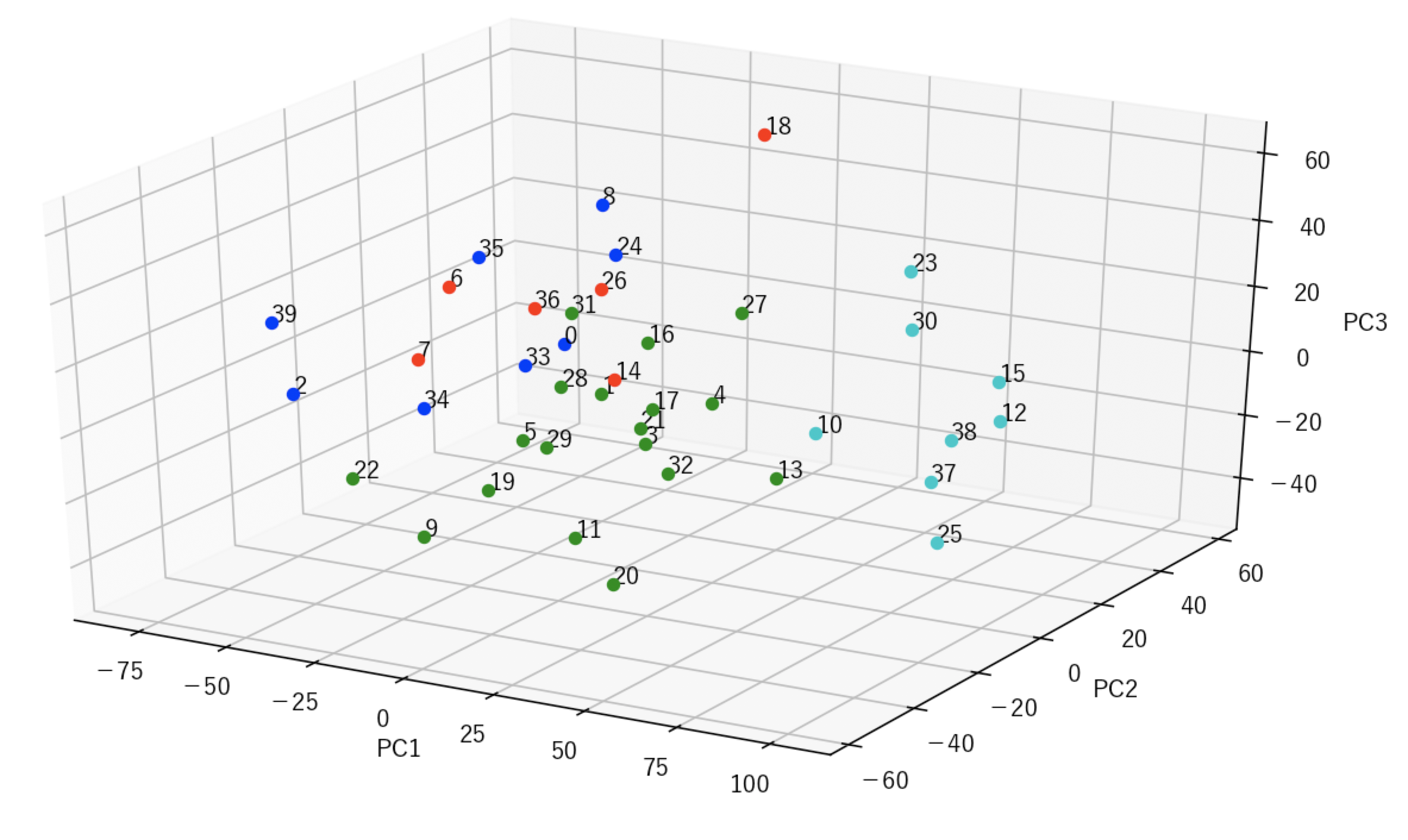
まずはグラフ描画を以下のように変更。
- 色用のlistを用意。
- plotではなくscatterで描画(for文の中で)
- k-meanの結果ラベルをDataFrameにjoin(今回はlabelとしてくっつけた)
fig = plt.figure(num=None, figsize=(15, 15), dpi=150, facecolor='w', edgecolor='k')
ax = fig.gca(projection='3d')
color_ = ["r", "g", "b", "c", "m", "y", "k", "w"]
for i in result.index:
ax.scatter(result.iloc[i].PC1, result.iloc[i].PC2, result.iloc[i].PC3, marker="o", linestyle='None', color=color_[result.iloc[i].label])
ax.text(result.iloc[i].PC1, result.iloc[i].PC2, result.iloc[i].PC3, result['name'][i])
print(result.describe())
ax.set_xlim(result.describe().at['min', 'PC1']-10, result.describe().at['max', 'PC1']+10)
ax.set_ylim(result.describe().at['min', 'PC2']-10, result.describe().at['max', 'PC2']+10)
ax.set_zlim(result.describe().at['min', 'PC3']-10, result.describe().at['max', 'PC3']+10)
ax.set_xlabel('PC1')
ax.set_ylabel('PC2')
ax.set_zlabel('PC3')
plt.show()
上と下で色の違いはありますが。。
28と18の結果は違う事はわかる。。。うーん。。
まとめ
よく出したけど、結局わからず。そりゃそうですよね。どうクラスタリングされるのが正解かわからない状態でやっているので・・・。
けどなんか面白かったので記事にしてみました。
色々勉強になりました。
(もう少し、主成分分析とk-meansを数学的に理解すれば、この違いも説明できうる!?)
補足
Macでmatplotlibで日本語出す時に困ったのでそのメモ。 Fontを追加した後は忘れずにキャッシュファイルを消す。
rm ~/.matplotlib/fontlist-v300.json