ニューラルネットワークの出力層設計に関する指針

#概要

　近年，DeepLearningに代表されるニューラルネットワーク関連技術の発展が目覚ましい．今まで，過学習により十分な精度が出なかったニューラルネットワークがHintonらのDropLearningやAutoEncoderなどの手法で，汎化能力を損なわぬまま，高い制度の学習能力を獲得することができるようになった．また，近年のGPGPUの発展やTensorflow等のライブラリの整備により，大規模なニューラルネットワークの学習も比較的容易にできるようになった．
　その一方で，ニューラルネットワークの学習手法には多くの関心が払われる中，それらのニューラルネットワーク自体の階層構造や，パーセプトロンの個数に関する議論というものは，あまり行われていない．近年ではLSTMやCNN等応用したニューラルネットワークの存在も見られるが，実際にそれらの精度を高めるための設計指針については，職人芸を要するのは旧来から変わっていない．
　本文章では，モデル化したニューラルネットワークの出力層設計についてZ3 Solverを用いて議論を行う．そのうえでZ3 Proverにより，指定の精度のニューラルネットワークを構築するために指針となる手法，およびプログラムを示します．

#モデル化したニューラルネットワークの導入
##誤差なしの回帰モデル
非常に基礎的なニューラルネットワークを導入します．ここで，議論するのはニューラルネットワークによる回帰問題を取り扱います．

図のように出力層に3つのパーセプトロンを持ち，それぞれの出力に重み係数がかけられ，それらの総和と定数を足したものがoutputが出力されます．数式で書くと以下のようになります．

\begin{split}
u_i \in \{ 0 , 1 \}  \\
output = \sum_{i=1}^{3} u_i w_i + c
\end{split}

###パーセプトロン数に関する議論
ここでは，$u_i$はいわゆるステップ型のパーセプトロンで，0か1の値しかとらないものだとします．
このようなニューラルネットワークで，

( \vec{x_1} , y_1 ), ( \vec{x_2} , y_2 ), ( \vec{x_3} , y_3 ), ( \vec{x_4} , y_4 )

という4つのデータを回帰することについて考えます．パーセプトロンの入力として$\vec{x_i}$を受け取り，$y_i$を出力するとします．この時**$ y_1, y_2, y_3, y_4 $ に注目し，$\vec{x_1},\vec{x_2},\vec{x_3},\vec{x_4}$に関しては無視します．**
以上のような条件で，パーセプトロンによる回帰を行うことを考えます．今，対象としているニューラルネットーワークの出力層は3つのユニットから構成されます．この時，$u_1,u_2,u_3$のとりうる状態は高々8通りです．$y_i \neq y_j (i \neq j)$が成り立つとき，誤差なく回帰ができる最大の数は8にすぎない．ということです．当たり前のことですが以下のことが分かります．

出力層のパーセプトロンが$n$個の時,誤差なく回帰ができるデータセットの最大の個数は$2^n$個にすぎない．

ということです．ここから，注目すべきパラメーターはデータセットの個数ということが分かります．そして，そこから，出力数のパーセプトロンの数が導くことが出来ます．ここで，データセットの個数を$m$としたとき，誤差なく回帰できる出力数のパーセプトロンの数を$n$とすると，

n \geq \lceil \log_{2} m \rceil

の関係式が分かります．これにより$n$に関する下限値が求めることが出来ました．一方で，上限値は，$m$個のデータに対し，それぞれ0,1を割り当てることと同等なので，

m \geq n \geq \lceil \log_{2} m \rceil　\tag{1}

ということが分かりました．

###回帰に関する最適化問題の議論
パーセプトロンによる回帰には2つの問題によって構成されます．

1. 符号の割り当て
2. 回帰係数の最適化

先にあげた例を用いて，説明します．ここで変数 $s_{i,k}$を導入します．

\begin{split}
s_{i,j} \in {0,1} \\
y_k = \sum_{i=1}^{n} s_{i,k}w_i + c
\end{split}

データ$y_k$を回帰するとき，$u_i$の出力を$s_{i,k}$と定義します．ここでは，この式を「スタート制約式S」と便宜上呼びます．
先ほどの例を全部書き下すと，

\begin{split}
y_1 = s_{1,1}w_1 + s_{2,1}w_2 + s_{3,1}w_3 + c \\
y_2 = s_{1,2}w_1 + s_{2,2}w_2 + s_{3,2}w_3 + c \\
y_3 = s_{1,3}w_1 + s_{2,3}w_2 + s_{3,3}w_3 + c \\
y_4 = s_{1,4}w_1 + s_{2,4}w_2 + s_{3,4}w_3 + c 
\end{split}

となります．ここで，$y_i$を回帰する際に，$s_{i,j}$の内容をどのように決定するか？という問題が1つ生まれます．これが先ほど上げた「符号の割り当て」という問題．仮に，$y_1$に対し，$s_{1,1}=0$，$s_{2,1}=1$，$s_{3,1}=1$という符号を割り当てたときに，$w_1$,$w_2$,$w_3$,$c$の値をいくつにするのか？という問題が生まれます．これが先ほど上げた「回帰係数の最適化」に当たります．これらを同時に解くアルゴリズムを考えることは非常に難しい．そこで，SMTソルバーを用います．

1. スタート制約式Sを定義します．ただし，$n=m$として定義します．
2. $E_{min} = \lceil \log_{2} m \rceil$ とする．
3. $E_{max} = m$ とする．
4. $E_{try} = {E_{min} + E_{max} \over 2 }$とする．
5. $w_i=0 (i>E_{try})$として，制約充足性を判定する．
6. 論理式が充足だった場合，$E_{max} = E_{try}$, 出来なかった場合，5.の制約式を除外し，$E_{min} = E_{try}$とする．
7. $E_{max} - E_{min} = 1$ならば8.へ．そうでないとき4.へ．
8. $y_i$を回帰できる最小のユニット数は$E_{max}$であることが分かる．

いわゆる二分探索を行い，データ$y_i$を表現するのに必要な最低のユニット数$n$を求める．その際に，先ほど用いた(1)式を用いて，下限上限を与えている．

##誤差ありの回帰モデル
この章では誤差ありの回帰モデルについて議論する．前述した誤差なしの回帰モデルで表されるのはごく稀で，一般的には誤差を含むモデルを用いることが多い．ここで，設計上許容できる誤差を$\epsilon$と定義する．この時，制約式は

\begin{split}
y_k - \epsilon \leq \sum_{i=1}^{n} s_{i,k}w_i + c \leq y_k + \epsilon
\end{split}

となる．この式を「スタート制約式$S'$」と定義する．これを先ほどのアルゴリズムと同様に計算すると，誤差$\epsilon$以内の精度のパーセプトロンが設計できる最小の数$n$を求めることが出来る．ここで，先ほど議論した「スタート制約式$S$」は「スタート制約式$S'$」の$\epsilon=0$の時の特殊なパターンであることが分かる．

#実際のコード

今回，データとして

のUSDJPYの日足データを16日分，利用しています．その中で１日の終値に対し，誤差は0.1円以内として適用しています.

#coding:utf-8
from z3 import *
from math import log,ceil

def cluster(max_epsilon,data,solver):
    n = len(data)
    epsilon = Real("epsilon")
    constant = Real("constant")

    max_n = n
    min_n = int(ceil(log(n,2)))
    weights = [
        Real("weight_%04d" % i)
        for i
        in range(n)
    ]

    solver.add(epsilon >= 0)
    solver.add(max_epsilon >= epsilon)

    all_vals = []

    for idx,d in enumerate(data):
        print idx,len(data)
        vals = [
            Real("val_%04d%04d" % (idx,i))
            for i
            in range(n)
        ]

        all_vals.append(vals)

        for val in vals:
           solver.add(Or(val == 1.0,val == 0.0))
            
        solver.check()

        out = sum(v*w for v,w in zip(vals,weights)) + constant

        solver.add(
            d - epsilon <= out , out <= d + epsilon
        )

        solver.check()


    while max_n != min_n:
        try_n = (max_n + min_n) / 2
        solver.push()
        expressions = [
            weights[i] == 0
            for i
            in range(try_n,n)
        ]

        print expressions

        solver.add(
            expressions
        )

        print min_n,max_n,try_n

        if s.check() == sat:
            print "ok:",min_n,max_n,try_n
            max_n = try_n
            s.push()
        else:
            print "ng:",min_n,max_n,try_n
            min_n = try_n
            s.pop()

    print "max_n:",max_n
    print "constant:",float(solver.model()[constant].as_decimal(15)[:-1])
    model = solver.model()
    print "weights:"
    for w in weights:
        print w,model[w].as_decimal(15)[:-1]
    print

    print "patterns:"
    for line in all_vals:
        print "".join(str(int(model[v].as_decimal(15))) for v in line)

       

if __name__=="__main__":
    s = Solver()

    data = []
    with open("tmp.csv") as f:
        f.next()
        for l in f:
            data.append(float(l.split(",")[5]))
        
    data = data[:16]
    data.sort()
    
    cluster(0.1,data,s)

実際の出力は

kotauchisunsun@kotauchisunsun-VirtualBox:~/z3nn$ python nn_cluster2.py 
0 16
1 16
2 16
3 16
4 16
5 16
6 16
7 16
8 16
9 16
10 16
11 16
12 16
13 16
14 16
15 16
[weight_0010 == 0, weight_0011 == 0, weight_0012 == 0, weight_0013 == 0, weight_0014 == 0, weight_0015 == 0]
4 16 10
ok: 4 16 10
[weight_0007 == 0, weight_0008 == 0, weight_0009 == 0, weight_0010 == 0, weight_0011 == 0, weight_0012 == 0, weight_0013 == 0, weight_0014 == 0, weight_0015 == 0]
4 10 7
ok: 4 10 7
[weight_0005 == 0, weight_0006 == 0, weight_0007 == 0, weight_0008 == 0, weight_0009 == 0, weight_0010 == 0, weight_0011 == 0, weight_0012 == 0, weight_0013 == 0, weight_0014 == 0, weight_0015 == 0]
4 7 5
ok: 4 7 5
[weight_0004 == 0, weight_0005 == 0, weight_0006 == 0, weight_0007 == 0, weight_0008 == 0, weight_0009 == 0, weight_0010 == 0, weight_0011 == 0, weight_0012 == 0, weight_0013 == 0, weight_0014 == 0, weight_0015 == 0]
4 5 4
ok: 4 5 4
max_n: 4
constant: 89.5
weights:
weight_0000 1.4
weight_0001 -0.6
weight_0002 -0.1
weight_0003 -0.8
weight_0004 
weight_0005 
weight_0006 
weight_0007 
weight_0008 
weight_0009 
weight_0010 
weight_0011 
weight_0012 
weight_0013 
weight_0014 
weight_0015 

patterns:
0111101001011111
0011010111111111
0110000111011001
0001110111011110
0100001011101010
0110111001110011
1111001010111011
0000010010100000
0000010110111111
1011100000110011
1001101000010111
1100110001100100
1010011010110111
1010110101000010
1000010110001011
1000110010010001

結果のみを抜粋し，まとめると

output = 1.4 u_1 -0.6 u_2 -0.1 u_3 -0.8 u_4 + 89.5

終値	$u_1$	$u_2$	$u_3$	$u_4$
87.87	0	1	1	1
88.37	0	0	1	1
88.61	0	1	1	0
88.7	0	0	0	1
88.77	0	1	0	0
88.79	0	1	1	0
89.17	1	1	1	1
89.47	0	0	0	0
89.64	0	0	0	0
89.86	1	0	1	1
90.09	1	0	0	1
90.32	1	1	0	0
90.71	1	0	1	0
90.84	1	0	1	0
90.9	1	0	0	0
91.08	1	0	0	0

という形になります．ここで16個のデータが誤差0.1以内で4つのパーセプトロンで表現できることが分かります．

#手法の制限と限界
この手法により最小化したパーセプトロンの数，その時の重み係数と，パーセプトロンの発火パターンを得ることが出来ます．しかし２つの制限事項があります．

1. 小規模の問題にしか適用できない
2. パーセプトロンの表現能力しか議論していない

1.に関していうと，これは利用しているZ3 Proverの限界です．上記のサンプルプログラムでは，誤差の範囲を0.01にまで絞ってしまうと，30分以上答えの出力に時間がかかります(それ以上は時間がかかりすぎたため求解できたかは未確認)．もう少し実装方法や論理式の組み立てをこだわると早くなるかもしれません．2.に関していうと，今までの文章は回帰能力については議論していません．ただ回帰をするためには，出力層において，少なくとも「回帰したいデータの表現能力」を持っていることが前提となります．その「出力層に回帰したいデータの表現能力を持っているか？」ということについてこの文章で議論しているにすぎません．

#ニューラルネットワークの緩和問題としての利用
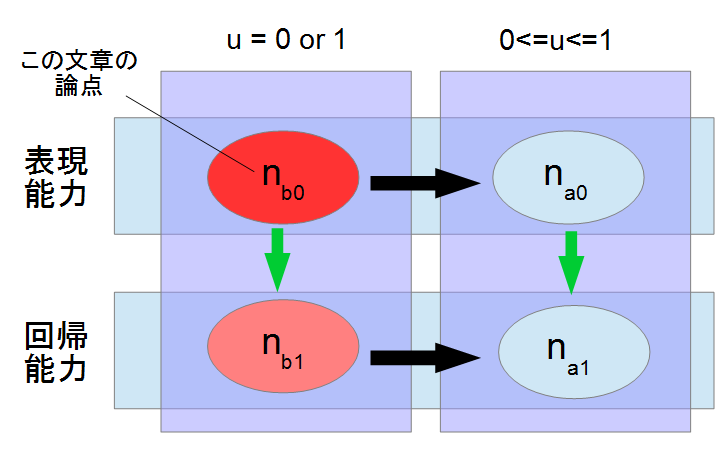
今回議論したパーセプトロンの議論は，基礎的なモデルです．現在よく使われているパーセプトロンの識別関数は，シグモイドであったり，tanhの場合のほうが多いです．ここで下の図を見てください．

今回，本手法で分かったパーセプトロンの数は，"出力層の表現能力を表すために必要なパーセプトロンの数"ということで，$n_{b0}$とします．しかし，一般的に求めたいデータは$n_{b1}$に当たる数です．その時，"おそらく"次の一般式が成り立ちます．(左緑矢印)

n_{b0} \leq n_{b1}

"おそらく"という但し書きがあるのは，証明はしていないからです．回帰に関する議論として，別軸で汎化性能について議論していません．データを回帰する際，細かなコーナーケースを表現するために，おそらく上記の式が成り立つであろう．という予測です．
ここで，もう1つ議論が可能で，パーセプトロンの識別関数を$0 \leq u \leq 1$に拡張したとき，回帰するデータを表現するのに必要なパーセプトロンの数を$n_{a0}$と定義します．これは，

n_{b0} \geq n_{a0}

が成り立ちます．(上黒矢印)これは，$n_{b0}$が識別関数を0,1の2値しか取れないのに対し，$n_{a0}$の識別関数は0から1までの範囲を取れます．少なくとも前者の識別範囲の値域は後者の識別関数の値域の一部範囲にすぎないため，後者の$n_{a0}$のほうが表現能力が高く，より少ないパーセプトロンの数で表現が可能であるため，上記の式が成り立つと考えられます．また，$n_{a0}$に関しても$n_{b0}$と同様の議論が可能で，

n_{a0} \leq n_{a1}

(右緑矢印)．また，$n_{b0}$と$n_{a0}$と同様の議論から，

n_{b1} \geq n_{a1}

という関係式が分かります．(下黒矢印)
これらの式をまとめると

\begin{split}
n_{a0} \leq n_{b0} \leq n_{b1} \\
n_{a0} \leq n_{a1} \leq n_{b1}
\end{split}

ということが分かります．現状，(1)式の条件から，データ数が$m$の時，パーセプトロンの数$n$は

m \geq n \geq \lceil \log_{2} m \rceil

ということしかわかりませんでした．しかし，ここで$n_{b0}$の値が上記手法により算出できることで，より$n_{a0}$の範囲を限定できることが分かります．

n_{b0} \geq n_{a0} \geq \lceil \log_{2} m \rceil \tag{2}

今回用いた識別関数は非常に限定されたモデルで，一般的なモデルを用いてパーセプトロンの数を議論することに比べるとコストが軽いことがメリットとして挙げられます．また(2)式のように上限の値を小さくすることが出来ることがメリットで，$m$が非常に大きいとき，$m >> log_{2} m$となってしまい，そのまま，一般的なモデルで議論してしまうと，$n$の範囲が広すぎるため，非常に時間がかかることが考えられます．そこで，今回用いた基礎的なモデルを一度経由し，上限を与えることで，効果的に設計できると考えられます．

#まとめ

今回，この文章で議論したものは

1. 基礎的な識別関数を持つパーセプトロンの表現能力について議論した
2. 1.のモデルについて，与えられたデータを最低限表現する，最小のパーセプトロン数を求める方法を示した
3. 一般的な識別関数をもつパーセプトロンの数についても，2.の結果を用いることで効率的に絞り込めることを示した

おそらく$n_{b0}$が求めることが出来た場合，$n_{a1} = n_{b0}$を初期の設計として問題はないと思われる．その理由として，今まであまり理由付けなく，経験的にパーセプトロンの数が選ばれていたため，1つの指針として，$n_{b0}$を使うのは，方針として選ぶ価値はあると考える．

#今後の展開
今回，「パーセプトロンの表現能力」について議論した．しかし，「回帰能力」についてまでは議論できなかった．ここに関して簡便な方法が見つけることが出来れば，必要最小限のニューラルネットワークを構築し，学習コストも安く済むのではないかと考えられる．
また，Z3 Proverに依るところも多いが，より簡便な方法でこれらの設計を表記し，制約充足性により論理性を担保できれば，機械学習の高度な識別能力への貢献もあると考えられる．