LoginSignup
23
12

More than 1 year has passed since last update.

2021年のディープラーニング論文を1人で読むAdvent CalendarAdvent Calendar 2021Day 10
@koshian2(koshian2 ＠新刊通販中)

【ACGANの逆襲】新たな損失関数を導入してBigGAN超え！？

Last updated at Posted at 2021-12-09

2021年のディープラーニング論文を1人で読むAdvent Calendar10日目の記事です。ここから5回はGAN特集で、GANの論文を5連続で紹介していきます。GAN特集1回目はACGANの再評価論文です。ACGANとは古くからあった論文で、GANの生成と同時に画像分類をこなして、クラス単位での生成をするモデルでした。クラス単位の生成はConditional GAN（cGAN）の一種として捉えらますが、cGANの走りのような論文でした。ところが生成画像の多様性に問題があり、後続の研究でより性能のいいモデルが出てきてほとんど見向きされなくなったモデルでした。

この論文では、「Data-to-Data Cross-Entropy loss (D2D-CE) 」という新しい損失関数を導入することで、ACGANの性能を一気にBigGANに一太刀浴びせられるレベルへと引き上げます。またこの損失関数は汎用性が高く、訓練の安定性にも寄与し、StyleGAN2の性能をさらに引き上げることにも成功しています。一体どんな関数なのでしょうか。NeurIPS 2021のポスターに採択されています。著者は韓国の浦項工科大学校の方々です。

StudioGANは複数のGANを取り扱えるようにしたソフトで、その中にあります。

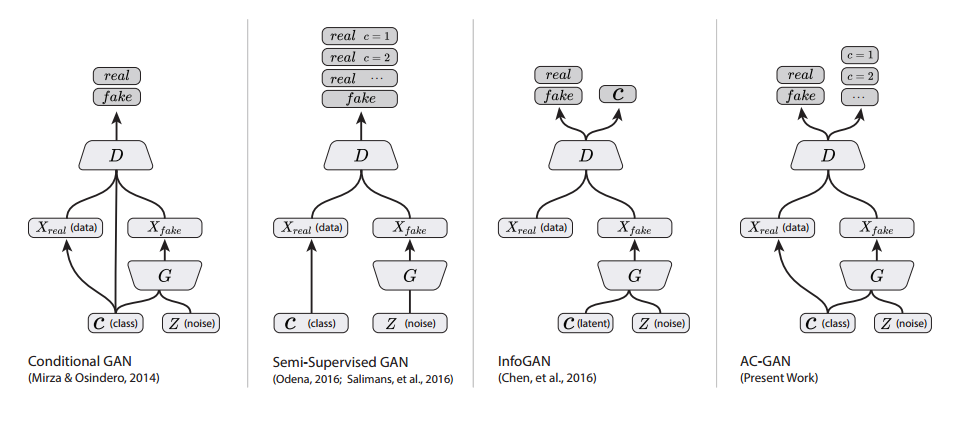
ACGANってなんだっけ？

ACGANの元論文はこちら。PyTorchによるACGAN実装より、

シンプルなGANではDはReal/Fakeを見分けるだけですが、ACGANではクラスも見分けます。Dで画像分類をしているのが特徴です。ただ、このACGAN、クラス内の画像の多様性を出すのに難有りで、クラス数を増やすと不安定さが増し、クラス内でのモード崩壊を起こします。そのため1000クラスあるImageNetの訓練で、10クラスごとにモデルを作り、100個のACGANをアンサンブルする形を取っています1。

ACGAN！？終わったはずでは……

ACGANの不安定さや出力画像のクォリティは後続の研究で改善されます。例えば後続のSelf Attention GAN（SAGAN）だと、

10_01.png

すでにボコボコにされています。Inception Scoreは高いほうが、Intra FID/FIDは低いほうがいいです。GAN界の革命児・BigGANだと

10_02.png

既にSAGANがベースラインで、ACGANは比較対象ですらありません。「ACGANなんか使ってるやつはアウトオブ眼中。頼まれたって実装なんかしねぇよ」という意味合いが微粒子レベルで入っているのかもしれません。

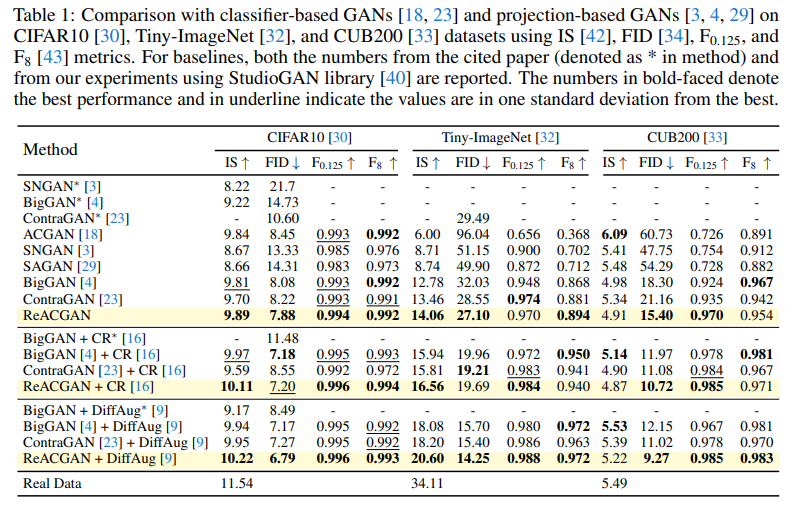
先に本論文の実験結果を見てみましょう。

10_03.png

「あれ、ACGAN思ったより悪くない！？」ということに気づきます。CIFAR10ではBigGANと同レベルありますし、後続のSAGANよりもいい部分もあります。Tiny-ImageNetではさすがにBigGANに大きく引き離されていますが。ちなみにReACGANというのが本論文です。

「SAGANの論文ではACGANボコボコにされているのに、この論文（ReACGAN）だといい勝負しているのなぜ？」と思うかもしれませんが、公平な評価をするためにReACGANの論文ではモデルのアーキテクチャを統一して実験しています2。また、Spectral Normalizationも基本的にGとDの両方（一部を除く）に入れています。ACGANがボコボコにされてしまったのは、モデル構造が原始的すぎたり、SNを入れてなかったからで、もう少しここらへんをちゃんとチューニングすれば、アウトオブ眼中では全然ないということが言えます。

本論文ではACGANの訓練がなぜ不安定になってしまったのかを述べ、その解決のためのシンプルな方法と、D2D-CEという新しい損失関数を提唱しています。

ACGANはなぜ不安定になったか

ソフトマックス＋クロスエントロピーに問題がある

ACGANの損失関数では、分類器（Auxiliary Classifier）の損失関数で、ソフトマックス関数のクロスエントロピーロスを使っています。数式で書けば、

\mathcal{L}_{ce}=-\frac{1}{N}\sum_{i=1}^N\log\Bigl(\frac{\exp(F(\boldsymbol{x}_i)^\top\boldsymbol{w}_{y_i})}{\sum_{j=1}^c\exp(F(\boldsymbol{x}_i)^\top\boldsymbol{w}_j)}\Bigr)

です。ここで$F$は特徴量の抽出器（Feature Extractor）とし、$F:\mathcal{X}\to\mathcal{F}\in\mathbb{R}^d$とします。$F(\boldsymbol{x}_i)$は$(N, d)$のshapeになります。これの偏微分は、

\frac{\partial\mathcal{L}_{CE}}{\partial\boldsymbol{w}_k}=-\frac{1}{N}\sum_{i=1}^N\Bigl\{F(\boldsymbol{x}_i)\Bigl(\boldsymbol{1}_{y_i=k}-p_{i,k}\Bigr)\Bigr\}

です。$\boldsymbol{1}_{y_i=k}$は$y_i=k$に1、それ以外は0を取ります。$p_{i,k}$は$i$番目のサンプルのクラス$k$に対する推定確率です。これがよくなくて、学習初期は$p_{i,k}$がどのクラスも小さい値でばらけているので、偏微分の値がとても大きくなってしまいます。これは勾配の大きさ$|\frac{\partial\mathcal{L}_{CE}}{\partial\boldsymbol{w}_k}|$が爆発してしまうことを意味しています。ACGANが学習の初期に崩壊してしまうのはこれが理由です。

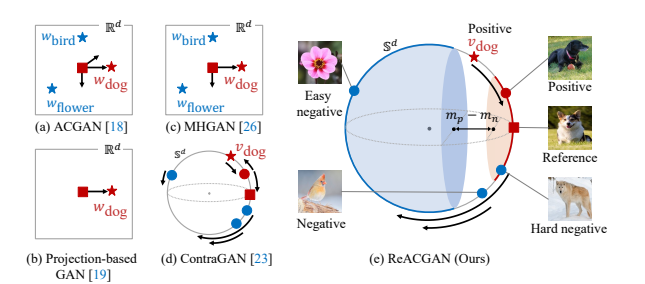
超球にプロットする

この解決方法は簡単で、特徴マップをノルムで正規化し、超球にプロットします。

$$\frac{F(\boldsymbol{x_i})}{|F(\boldsymbol{x_i})|}$$

これなら特徴マップのノルムは常に1になるからです。超球というと物騒な響きですが、多次元での円です。2次元でのノルムが1の点の集合が円です。

10_04.png

「正規化だけで本当に意味あるのか？」という点は疑問になりますが、この論文ではソフトマックスとソフトマックス＋正規化で定量的に比較しています。

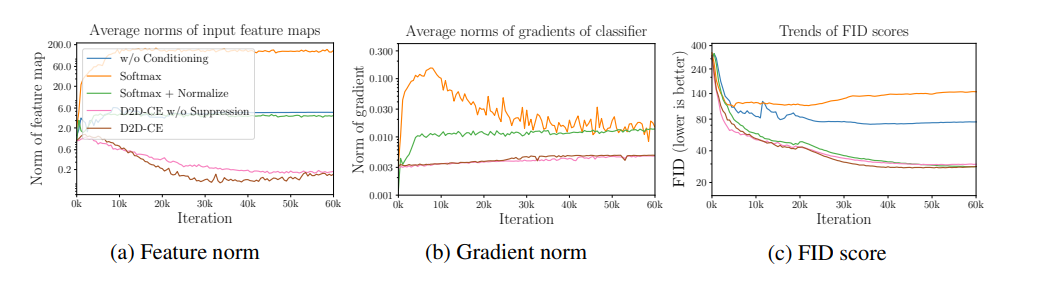
10_05.png

オレンジがソフトマックスだけ、緑がソフトマックス＋正規化です。Tiny-ImageNetでの実験です。特徴量のノルム（左）は正規化がないと爆発していますし、勾配ノルム（中央）も学習初期に大きくなっています。生成画像のクォリティが右ですが、勾配爆発を学習初期に起こした結果、FIDが下がらない＝意味ある生成画像を出さないという一連の流れが、理論と実験の両面から示されています。緑のケースではきちんとFIDが下がっており、勾配の大きさはほぼ一定で保たれています。この一連の説明は筋が通っていて明瞭で、個人的には唸らされました。

本論文では損失関数で2つの行列の類似度（行列積）を取る操作を行っています。本論文の実装では、コサイン類似度を類似度の関数として使っています。これも超球を満たします。なぜならコサイン類似度の値域は-1～1で、ノルムは1になるからです。

Data-to-Data Cross-Entropy Loss (D2D-CE)

モデル構成

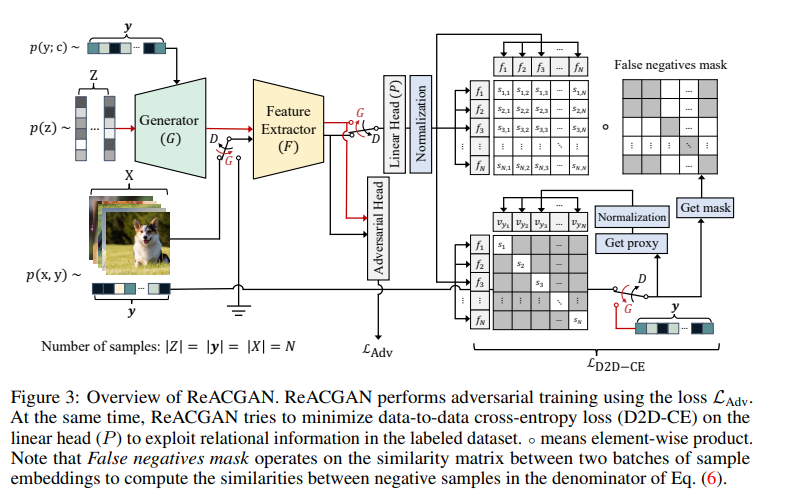
まずは本論文のモデルの構成を見てみましょう。

10_06.png

右上を見ると、サンプルごとの特徴量$f_1, f_2, \cdots, f_N$が総当りで計算されていますね。これが類似度の計算です。ACGANではDiscriminator（D）でクラスの分類を学習していましたが、ReACGANではクラス分類ではなく、各サンプルが同一のクラスに属するかどうかを学習しています。2つのサンプルが同一のクラスに属すればPositive、異なるクラスに属すればNegativeとなります。右上で総当りで計算しているのはPositiveかNegativeかの比較です。

この論文では明言されていませんが、発想的にはほぼ距離学習（Metrics Learning）なので、こちらの考え方を知っていると理解しやすいと思います。距離学習でもサンプル間のPositiveかNegativeを学習します。

「False negatives mask」があります。機械学習でのFalse negativeにならうなら「クラスが異なると判定されたが、実はクラスが同じだった」を意味しますが、この実装では単にGround Truthのクラスが異なるものを残すようなマスクです。これだとTrue negativeとFalse negativeの両方が残りますが、True negativeはマージンを使って抑え込みます。詳細は後ほど見ていきますが、サポートベクターマシンのようなマージンが入った距離学習のようなものと捉えておくといいと思います3。

「False negativeがあるならFalse positiveは見ないのか？」という点も気になりますが、サンプル数としてはFPよりFNのほうが多いため、FNだけ見ればいいのではないかと思います。Positiveの部分は、別の類似度の対角成分（サンプル内の特徴量同士の比較）を見ます。

D2D-CE Loss

本論文のコアの手法のData-to-Data Cross-Entropy loss (D2D-CE)は以下の定義です。

\mathcal{L}_{D2D-CE}=-\frac{1}{N}\sum_{i=1}^N\log\Bigl(\frac{\exp\bigl([\boldsymbol{f}_i^\top\boldsymbol{v}_{y_i}-m_p]_{-}/\tau\bigr)}{\exp\bigl([\boldsymbol{f}_i^\top\boldsymbol{v}_{y_i}-m_p]_{-}/\tau\bigr)+\sum_{j\in\mathcal{N}(i)}\exp\bigl([\boldsymbol{f}_i^\top\boldsymbol{f}_j-m_n]_{+}/\tau\bigr)}\Bigr)\tag{1}

ここで、

\boldsymbol{f}_i=\frac{P(F(\boldsymbol{x}_i))}{\|P(F(\boldsymbol{x}_i))\|}

と特徴抽出器の出力を、Projectionという別の層に通したもの$P(F(\boldsymbol{x}_i))$をノルムで正規化したものです。もう1個FCの層が加わったぐらいに見ておけばいいでしょう。

その隣の$\boldsymbol{v}_{y_i}$は何かというと、論文ではweight vectorとしか書いてありませんでしたが、実装を見るとラベルを埋め込み次元に落とした特徴量でした。自然言語処理で最初の層に入れるEmbedding層を思い出していただければイメージが伝わると思います。この埋め込み特徴量を$\boldsymbol{w}_{y_i}$とすると、それをノルムで正規化したもの、

\boldsymbol{v}_{y_i}=\frac{\boldsymbol{w}_{y_i}}{\|\boldsymbol{w}_{y_i}\|}

です。$\boldsymbol{f}_i$と$\boldsymbol{v}_{y_i}$のshapeは同じです。$\boldsymbol{w}_{y_i}$は$\boldsymbol{f}_i$の次元に合わせたラベルの埋め込み特徴量です。$\boldsymbol{w}_{y_i}$や$\boldsymbol{v}_{y_i}$のことを論文やコードではプロキシ（proxy）と呼んでいます。

$[\cdot]_{-}:\min(\cdot, 0), [\cdot]_{+}:\max(\cdot, 0)$を表します。$\tau$は温度を表す定数（ハイパーパラメータ）です。$m_p, m_n$はマージンを表す定数（ハイパーパラメータ）です。

分母の$\sum$の範囲$j\in\mathcal{N}(i)$は「$i$番目のサンプルとラベルが異なるサンプル$j$」を指します。False Negative maskの話がまさにここで、Negativeなもの全体を$j$に関する和の範囲として定めています。

ここの理解がハマったのですが、分母の$\boldsymbol{f}^\top\boldsymbol{f}$は行列を表すのに対し、それ以外の$\boldsymbol{f}^\top\boldsymbol{v}$はベクトルになります。後でコードを確認しますが、前者は$(N, N)$、後者は$(N, )$というshapeになります（正確に言えば対角要素を消すので$(N, N-1)$）。$(N, N)$のshapeの行列を$j$について和を取り、$(N, )$というshapeになります。初見は自分も意味不明だったので、簡単な例を作り、コードで見ていきましょう。

サンプルコードで理解するD2D-CEロス

公式コードのlosses.pyに実装がありました。これを参考にして簡単な例を作っていきます。

最初にコサイン類似度の計算用の関数を用意します。

import torch
import torch.nn.functional as F
import numpy as np

cosine_similarity = torch.nn.CosineSimilarity(dim=-1)

def calculate_similarity_matrix (x, y):
    return cosine_similarity(x.unsqueeze(1), y.unsqueeze(0))

ここでcosine_similarityとcalculate_similarity_matrixは別の使われ方をします。前者は$\boldsymbol{f}^\top\boldsymbol{v}$の計算用、後者は$\boldsymbol{f}^\top\boldsymbol{f}$の計算用として使います。前者は出力はベクトル、後者の出力は行列になります。

ff側の計算

簡単な例として乱数を用意します。バッチサイズ$N$が4、埋め込み次元数は16、クラス数は2とします。乱数で初期化しましたが、実際はembed, proxyはノルムで正規化済みとします。

# batchsize = 4, embed_dim = 16, classes = 2
embed = torch.randn((4, 16))
proxy = torch.randn((4, 16))
label = torch.randint(0, 2, size=(4,))
print(label) # tensor([1, 0, 1, 0])

またハイパーパラメータとして、温度$\tau$が0.5、マージンm_p=0.98, m_n=1-m_pとします。m_n=1-m_pとしたのはハイパラ探索の計算コストの関係だそうです。

m_p = 0.98
temperature = 0.5

次にサンプル間の類似度を取ります。これは$\boldsymbol{f}^\top\boldsymbol{f}$に相当するものです。

sim_matrix = calculate_similarity_matrix(embed, embed) + m_p - 1
print(sim_matrix)
#tensor([[ 0.9800,  0.0792,  0.4800,  0.0302],
#        [ 0.0792,  0.9800, -0.1400,  0.3366],
#        [ 0.4800, -0.1400,  0.9800,  0.1247],
#        [ 0.0302,  0.3366,  0.1247,  0.9800]])

当然のように対角要素だけ高くてあとは小さいです。乱数なので理論的には対角成分以外0になりますが、次元数を少なくしたので、そこそこありそうな値が出てきます。次に対角成分を取り除きます。本当は温度を加味するのですが、わかりづらいので最初は温度を1としてみます。

def remove_diag(M):
    h, w = M.shape
    assert h==w, "h and w should be same"
    mask = np.ones((h, w)) - np.eye(h)
    mask = torch.from_numpy(mask)
    mask = (mask).type(torch.bool)
    print(mask)
    return M[mask].view(h, -1)

# remove diagの挙動（温度1）
print(remove_diag(sim_matrix))

tensor([[False,  True,  True,  True],
        [ True, False,  True,  True],
        [ True,  True, False,  True],
        [ True,  True,  True, False]])
tensor([[ 0.0792,  0.4800,  0.0302],
        [ 0.0792, -0.1400,  0.3366],
        [ 0.4800, -0.1400,  0.1247],
        [ 0.0302,  0.3366,  0.1247]])

となります。対角成分以外が1つずつずれて、左に寄っているのが確認できます。(4, 4)のshapeの対角成分を消したので(4, 3)になっています。次に実装に忠実に温度を加味して対角成分を取り除きます。

# 温度を加味する
sim_matrix = remove_diag(sim_matrix/temperature) # (N, N-1)
print(sim_matrix)
#tensor([[ 0.1585,  0.9599,  0.0604],
#        [ 0.1585, -0.2800,  0.6732],
#        [ 0.9599, -0.2800,  0.2494],
#        [ 0.0604,  0.6732,  0.2494]])

温度はこれらの類似度を増強する効果があります。次の処理は数式にはなかったのですが、公式実装では安定性を増すために入れています。

# for numerical stability
sim_max, _ = torch.max(sim_matrix, dim=1, keepdim=True)
sim_matrix = F.relu(sim_matrix) - sim_max.detach()
print(sim_max)
print(sim_matrix)

tensor([[0.9599],
        [0.6732],
        [0.9599],
        [0.6732]])
tensor([[-0.8015,  0.0000, -0.8995],
        [-0.5148, -0.6732,  0.0000],
        [ 0.0000, -0.9599, -0.7105],
        [-0.6128,  0.0000, -0.4238]])

次にNegativeだけ残すようなマスクを作ります。make_index_matrixという関数を作り、

def make_index_matrix(labels):
    num_classes = 2 

    labels = labels.detach().cpu().numpy()
    num_samples = labels.shape[0]
    mask_multi, target = np.ones([num_classes, num_samples]), 0.0

    for c in range(num_classes):
        c_indices = np.where(labels==c)
        mask_multi[c, c_indices] = target
    return torch.tensor(mask_multi).type(torch.long)

1行ずつ実行していきましょう。

print(label)
index_matrix = make_index_matrix(label)[label]
print(index_matrix)
removal_fn = remove_diag(index_matrix)
print(removal_fn)

tensor([1, 0, 1, 0])
tensor([[0, 1, 0, 1],
        [1, 0, 1, 0],
        [0, 1, 0, 1],
        [1, 0, 1, 0]])
tensor([[1, 0, 1],
        [1, 1, 0],
        [0, 1, 1],
        [1, 0, 1]])

labelは[1, 0, 1, 0]でありましたから、最初のサンプルに対するNegativeなフラグは[0, 1, 0, 1]になります。ここでNegativeとは各サンプルとは異なるクラスであることを思い出してください。最終的にこれはsim_matrixに対して掛けたいので、対角要素を外してshapeをあわせます。

最後に指数をとり、ネガティブマスクとかけます。

# apply the negative removal to the similarity matrix
improved_sim_matrix = removal_fn*torch.exp(sim_matrix)
print(improved_sim_matrix) 
#tensor([[0.4487, 0.0000, 0.4068],
#        [0.5976, 0.5101, 0.0000],
#        [0.0000, 0.3829, 0.4914],
#        [0.5418, 0.0000, 0.6545]])

これが損失関数の分母にある$\sum_{j\in\mathcal{N}(i)}\exp\bigl([\boldsymbol{f}_i^\top\boldsymbol{f}_j-m_n]_{+}/\tau\bigr)$のシグマの中身になります。温度で割るのを括弧内でやっているのが異なりますが、結論は変わりません。

fv側の計算

同様に$\boldsymbol{f}^\top\boldsymbol{v}$側を計算します。こちらはベクトルになります。

smp2proxy = cosine_similarity(embed, proxy)
print(smp2proxy)
# tensor([-0.0381,  0.0517, -0.3833, -0.2063])

shapeはサンプルサイズの(4,)です。次にコードと式で異なるのですが、コードでは打ち切り処理をReLUでやっています。ReLUは$\max(x, 0)=|x|_{+}$であるため、

|x|_{-} = \min(x, 0) = -\max(-x, 0) = -|-x|_{+}

と変形して計算します。次のコードのsmp2proxyの符号がマイナスになっているのはこのためです。バグではありません。

# compute positive attraction term
pos_attr = F.relu((m_p - smp2proxy)/temperature) # min[x, 0]→ -max[-x, 0]
print(pos_attr)
# tensor([2.0363, 1.8566, 2.7267, 2.3726])

これは分子分母で使われます。

分子分母の統合

ここの実装は論文の式とはかなり変わるので混乱するところですが、論文とやっていることは一緒です。ただよく考えないとバグと勘違いするところです。

まず先に処理だけ見ます。これが損失関数の分母です。

# compute negative repulsion term
neg_repul = torch.log(torch.exp(-pos_attr) + improved_sim_matrix.sum(dim=1))
print(neg_repul)
tensor([-0.0142,  0.2342, -0.0621,  0.2543])

分子はそのままpos_attrを使います。最終的に損失関数の大きなシグマ（$i=1\to N$）の中身は、

# compute data to data cross-entropy criterion
criterion = pos_attr + neg_repul
print(criterion)
# tensor([2.0221, 2.0908, 2.6645, 2.6269])

という処理で表されます。あとはcriterionについて平均を取るだけです。

損失関数では分子分母だったのに割り算もしてませんし、全体のマイナスもかけていません。このつじつま合わせについてもう少し解説します。

数式とのつじつま合わせ

式(1)をコードに合わせて変形し、

\mathcal{L}_{D2D-CE}=-\frac{1}{N}\sum_{i=1}^N\log\Bigl(\frac{\exp\bigl([(\boldsymbol{f}_i^\top\boldsymbol{v}_{y_i}-m_p)/\tau]_{-}\bigr)}{\exp\bigl([(\boldsymbol{f}_i^\top\boldsymbol{v}_{y_i}-m_p)/\tau]_{-}\bigr)+\sum_{j\in\mathcal{N}(i)}\exp\bigl([(\boldsymbol{f}_i^\top\boldsymbol{f}_j-m_n)/\tau]_{+}\bigr)}\Bigr)

とします。温度の割る位置が変わっただけですね。式が長いので、

(\boldsymbol{f}_i^\top\boldsymbol{v}_{y_i}-m\_p)/\tau=A, \qquad (\boldsymbol{f}_i^\top\boldsymbol{f}_j-m_n)/\tau=B

とおきます。

\mathcal{L}_{D2D-CE}=-\frac{1}{N}\sum_{i=1}^N\log\Bigl(\frac{\exp\bigl([A]_{-}\bigr)}{\exp\bigl([A]_{-}\bigr)+\sum_{j\in\mathcal{N}(i)}\exp\bigl([B]_{+}\bigr)}\Bigr)

シグマの中の対数を外します。$\log(a/b)=\log a-\log b$、$\log\exp(a)=a$を利用します。

\mathcal{L}_{D2D-CE}=-\frac{1}{N}\sum_{i=1}^N\Biggl([A]_{-}-\log\Bigl\{\exp\bigl([A]_{-}\bigr)+\sum_{j\in\mathcal{N}(i)}\exp\bigl([B]_{+}\bigr)\Bigr\}\Biggr)

式中の$|\cdot|_{-}$をReLUにあわせて$|\cdot|_{+}$に変形します。

\mathcal{L}_{D2D-CE}=\frac{1}{N}\sum_{i=1}^N\Biggl([-A]_{+}+\log\Bigl\{\exp\bigl(-[-A]_{+}\bigr)+\sum_{j\in\mathcal{N}(i)}\exp\bigl([B]_{+}\bigr)\Bigr\}\Biggr)

ところで、コードでは$A$の部分を、

pos_attr = F.relu((m_p - smp2proxy)/temperature)

と、$-A$の形でReLUを取っていました。また$\exp\bigl(-[-A]_{+}\bigr)$の部分は、

neg_repul = torch.log(torch.exp(-pos_attr) + improved_sim_matrix.sum(dim=1))

と、torch.expの中でさらにマイナスを追加していました。したがって、このコードの実装はD2D-CEロスの定義通りというわけです。一見分子÷分母もしていないし、符号も怪しいしおかしな実装に見えるのですが、よく論文とコードを読み込むと正しいことに気づきます。

実験

この論文はあとはひたすら実験してます。

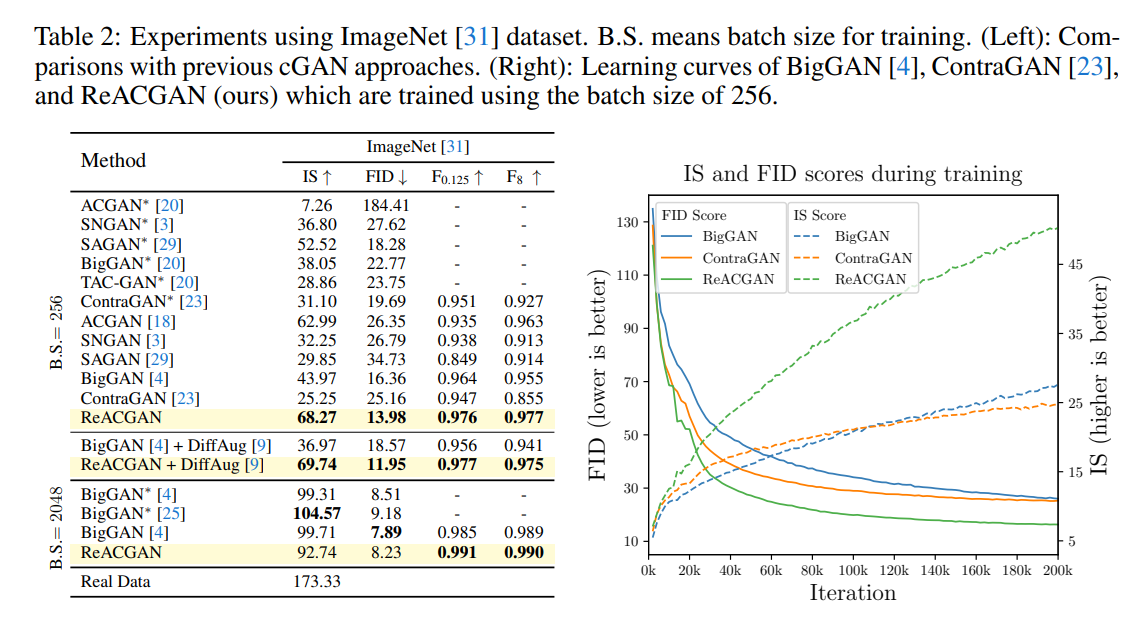
10_07.png

ImageNet 1K（普通に言うImageNet）での結果。BatchSizeが256のように低い場合に特に良い結果を出しています。BigGANではBSを上げることで勾配の信頼性を高め、出力画像の品質を上げていました。ReACGANが良い性能を出したのは、もしかすると新しいロスや正規化が勾配の信頼性を上げたのかもしれません。

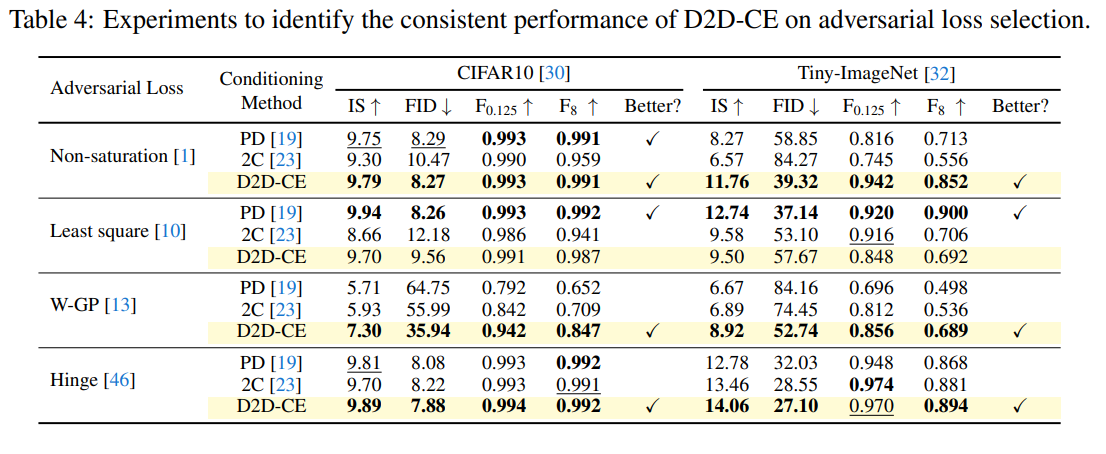
10_08.png

また、Adversarial Lossの選択に対してもおおよそ頑強な結果を見せました。

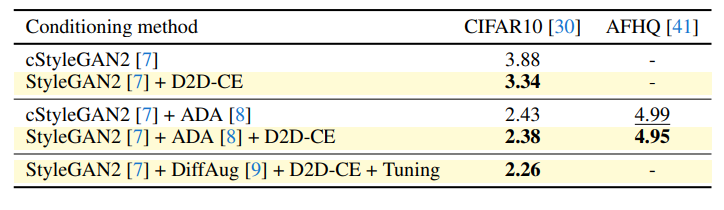
10_09.png

面白いのがStyleGAN2のようなアーキテクチャでもD2D-CEは効くということです。cStyleGAN2＋DiffAugは見る必要ありそうですが、入れただけでFIDを15％ぐらい落とすのは結構すごい。

10_10.png

生成画像。ACGANとは思えないクォリティ。ただモデルや訓練設定がほぼBigGANなので、BigGANを少し良くぐらいは当然出ます。

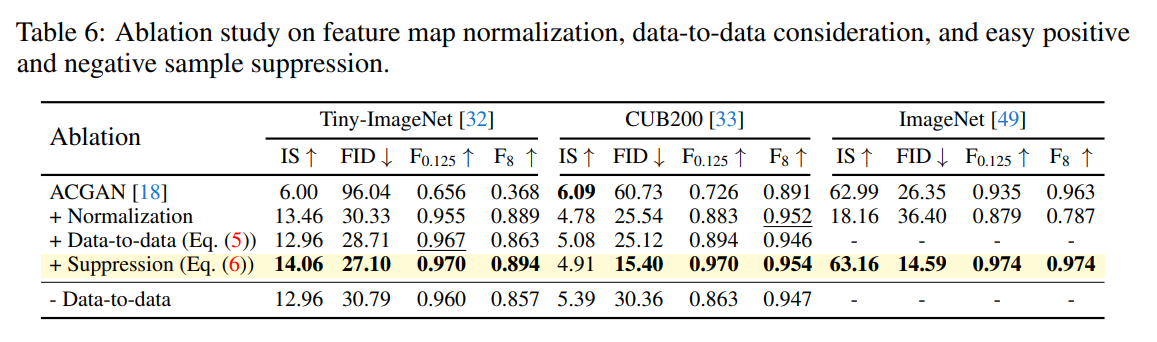
10_11.png

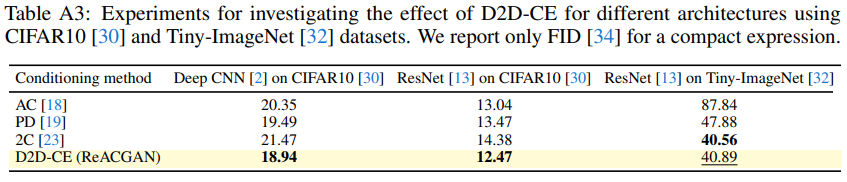
この論文でのアイディアの検証。Normalizationが大きく効いているように見えます。ただ、他のテーブルのACGANの結果とだいぶぶれているので、ベースラインの設定がどんなものかは気になります。Tiny ImageNetが一番自然な結果です。

10_12.png

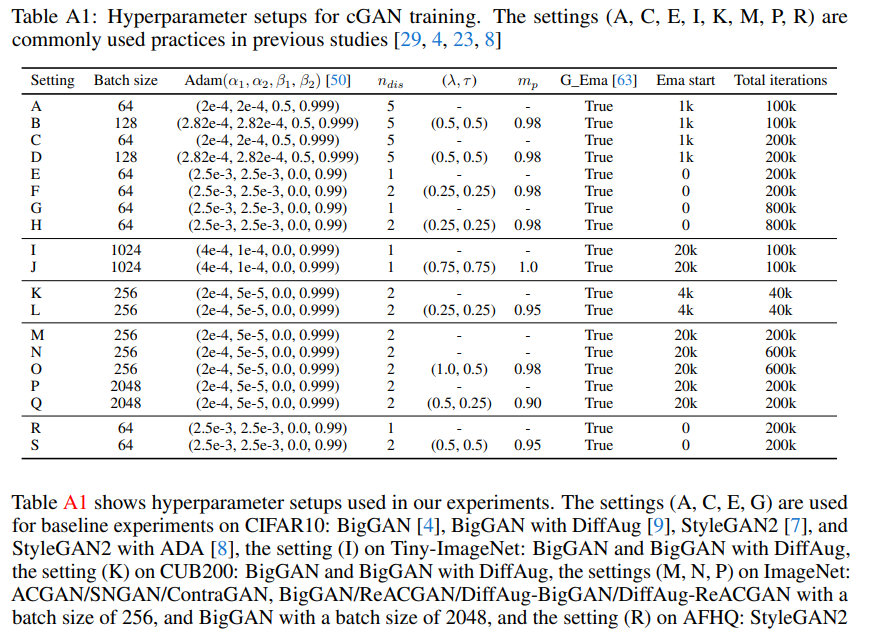
訓練中にDを複数（$n_{dis}$）回アップデートしていますが、これはSpectral Normalizationを入れている関係です。実際にハイパラを見ると、

10_13.png

表にデータセットやモデル入れればもう少しわかりやすくなるのですが、$\lambda, \tau$があるのがReACGANでしょう。$n_{dis}=2$をよく使っていてこの訓練設定はBigGANに似ています。GにEMA入れているのもBigGANっぽいです。

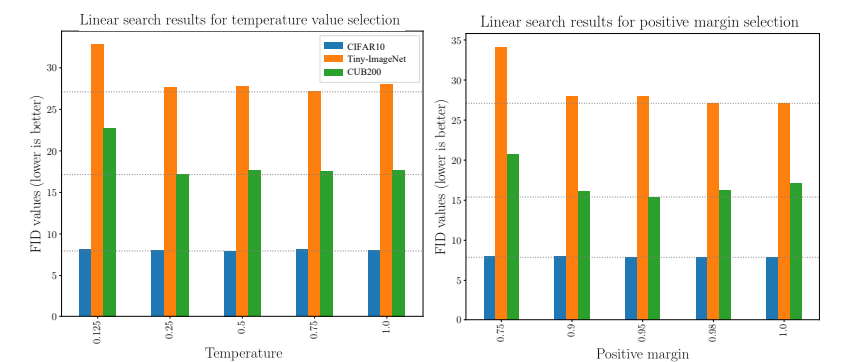
10_14.png

温度、マージンのハイパラ探索です。良くなるハイパラの値はあるものの、「このハイパラ設定でないと訓練に失敗する」というような強い依存性はありません。

10_15.png

ネットワークのアーキテクチャに対する評価です。ResNetでもDeepCNNでもほぼ同じような傾向になっています。

10_16.png

損失関数内でのNegativeサンプルのマスクの比率とFIDです。この論文では損失関数の計算で、全てのNegativeサンプルのペアを使用していますが、もしこれらのNegativeなサンプルを一部落としたらどうなるのかという実験です。例えば$p=0.1$なら、Negativeサンプルの1割を落とすということです。実際、$p=0$が最もよく、すべてのNegativeサンプルを使ったほうがよい性能がよくなることを表しています。これはより多くの関係性を学習できるからです。

興味深かったのが計算量の記述です。V100を8個で計測したそうですが、バッチサイズを2048でImageNetの100回のGのアップデートに必要な時間は、BigGANが17分37秒、ContraGAN（著者の以前の研究）18分24秒、ReACGANが18分52秒でした。7%程度計算量が増えていますが、これはロスで潜在次元の行列積を取っているため致し方ないのかなと思います。しかし、多くのケースで200kアップデートしているので、これらのGANの研究に必要な計算資源はお察しなレベルですね。GAFAに研究を寡占されないことを祈ります。

10_17.png

実際にこんなテーブルを出しているぐらいなので、本当に計算リソースが足りないと思います。実際に自分もそうしていますが、CIFAR10で多く回しているのは計算量的にリーズナブルだったからでしょう。AFHQ+StyleGANとImageNetで1桁ぐらい計算量が違うのは、AFHQのデータ数が1.5万枚だからです。モダンなCVの問題として、正確な評価をするにはImageNet 1Kでやるのが正しいのでしょうが、ImageNet 1Kを回そうとすると1回だけで2週間かかってしまうのは厳しすぎますね。これだけGPUを投資してこの程度なので、日本のような貧弱な研究基盤だととてもではないけど研究できないと思います。

まとめと感想

この論文ではD2D-CEという、サンプル間の関係性を学習する新しい損失関数を導入し、GANでの一定の有用性を示しています。その上でACGANの再評価の可能性を示しています。ACGANの勾配の爆発についての理論的な説明はなかなか唸らされるものがありました。Appendixで追加実験を多く行っており、レビュアーに指摘されてやったのか最初からやったのかは不明ですが、これだけいろんな実験を頑張ったのはすごいですね。

個人的にはかなり好きな論文なのですが、NeurIPS2021のレビュアーは激辛評価でした。ここまで内容の濃い内容だと最初ポスターではなく、普通のフルペーパーとして出したのかなと思ってOpenReviewを読んでみました。ポスターとしてはアクセプトできる内容だが、他の委員会ではリジェクトされてしまいました。

理由の一つは先行研究とのContraGANとの違いがわからないとのこと。ちなみにContraGANとReACGANの著者は同じです。ContraGANの中でアイディアがいろいろ検討されてあったから、それが仇となってより違いがわからなくなってしまったのかもしれません。多分著者のお気持ち的には、そのアイディアをよりちゃんとしたものにしたのが、この論文ではないかと思います。ContraGANの論文流し読みした感じでは、こっちも力作で、いろいろ実験したのを載せたいタイプの頑張り屋さんなのかもしれません。

図をもう少しわかりやすく書いたり、仮説検証の流れをもう少しはっきりすれば、多分もうちょっと良い評価が出たと思います。その点では結構もったいない論文かなーと思います。レビュアーの評価を見ていると読んで2～5時間程度なので、自分がやったようなコードと実装の突き合わせをレビュワーはほぼやっていないと思います。自分が1日近くかけて読んでもContraGANとの違いはいまいちよくわからなかったので、レビュアーにはもっと伝わっていないのではないでしょうか。使う側からすると「違いがわからなくても、いいほうのReACGANでいいじゃん」になるのですが、論文だとそこは重要な問題なのでしょう。

ただ、レビュアーが指摘している「これは本当にACGANのRebootingなのか？　誤解を招くのでは？」はたしかに一理あるなーと思いながら見ていました。FUNITやStarGANv2に代表されるマルチタスクなDが最近の強力な手法と書かれていました。ただし、ACGANのモデルをしっかりして再実装したらそこまで悪くないですし、ACGANもクラス分類と真偽の分類のある意味マルチタスクなので、もしかすると今後再評価されてくるのかもしれません。

告知

このアドベントカレンダーが本になりました！
https://koshian2.booth.pm/items/3595424
Amazonでも扱いあります詳しくは👉　https://shikoan.com

  1. GANの生みの親であるIan Goodfellowはこの分け方について「ある種のチート」と述べています 　https://openreview.net/forum?id=B1QRgziT- ↩

  2. どういったアーキテクチャを使ったかは明確にわかりませんでしたが、コードを読んでいるとResNetベースを使っているのではないかと思われます ↩

  3. 似た例だと距離学習の典型例のTriple lossですね。これはマージンを含めて学習します。ただこれは3点間の比較はしていないのでTripletではありません。 ↩

23
12
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
23
12