CIFAR-10で「天然物か人工物かどうか」のフラグを入れて分類すると精度が上がるか？ #Python

前回のランドマーク検出で、「実は損失関数を改造すると収束が速くなる、良くなることがある」というのを確認できました。今回はそれを分類問題にも適用してうまくいくのかどうかを軽く検証します。

結果だけ読みたい方は「結果」のとこまで飛んでくださいね。結論から言うと上がります。

訓練時にはラベルが何かだなんて一切教えていない

ここにCIFAR-10の画像一覧があります。CIFAR-10の公式サイトからです。

人間がこれを見ると、1番目は飛行機で2番目は自動車で3番目は猫で…と、クラスごとに飛行機、自動車といったラベル名が対応付けられているように見えます。しかしこんなの訓練時には一切教えていないんですよね。だから、機械学習やディープラーニングでラベルと呼んでいるものは、あくまで「なんかそれっぽい区分けが10個あって、これとこれとこの画像は1番目の区分け、この画像は2番目の区分けに行くように最適化しなさい」ということだけで、「これが猫でこれが犬だ」と教えているように錯覚するのは、我々人間の勝手な思い込みではないのでしょうか。

人間はカエルとトラックを見間違わない

この教え方だと、トラックもカエルも同じ1つのクラスでしかないわけです。したがって、「カエルとトラックを間違える」というようなケースも起こりえます。でも人間が自動車とトラックを見間違えることはあっても、カエルとトラックを見間違うなんてことは普通はないですよね。

ではなぜないかというと、自分は認知科学は素人なのですが、まず「天然物かどうか人工物かどうか」というような先入観があるのではないかと思うのです。例えば道路の上に物体があれば、「まずここにあるのは人工物だ」というような先入観が働くはずです。つまり道路の画像を見せられた時点で、そこにカエルのズーム画像が出てくるという選択肢は頭の中でズバッと切っている（取捨選択している）のではないでしょうか。こうやって事前に情報の取捨選択しているから、人間は高速にいろんなものを認識できるのかなーとも思います¹。

「天然物かどうか人工物か」どうかのフラグを与えて訓練させたらどうか

ひとまず人間の脳や認知の構造がどうだということは置いておきましょう。あくまで「ニューラルネットワークにこれは猫でこれは犬だと教えているように見えるのが人間に思い込みだよ」ということを伝えたかったのです。

では逆の発想で、「天然物か人工物かどうか」というフラグが、ニューラルネットワークがクラス分類する際に有効に機能するのではないかとも考えられるのです²。つまり、天然物のクラスに属したかどうか、人工物のクラスに属したかどうかという追加情報を損失関数に与えることで、学習をよりブーストさせる、つまりネットワークに対して大きな勾配を与えられることができ、学習を高速化させるのではないかという発想ができます。

「天然物かどうか人工物かどうか」なんて人間が手助けしてやれば簡単です。順に、飛行機(0)、自動車(1)、鳥(2)、猫(3)、鹿(4)、犬(5)、カエル(6)、馬(7)、船(8)、トラック(9)なので、2番目から7番目までが天然物です。クラスのインデックスを$d$とすれば、天然物であることを$y=1$とすれば

\begin{cases}
y=1\qquad \rm{if}\quad 2\leq d\leq7 \\
y=0\qquad \rm{otherwise}
\end{cases}

ちなみに10個のクラス全体が最適解（真のクラス＝予測クラス）であるとき、この天然物か人工物かどうかという分類も最適解になります。あくまで天然物か人工物かというのは、10個のクラスが最適解に向かうようサポートしてあげることなのです。

ソフトマックス版

これをKerasの損失関数で書くとこうなります。今、y_trueが(None, 12)のshapeで「10個のクラス+天然物かどうか(0,1)+人工物かどうか(0,1)」であるとしましょう。これはジェネレーターを自作して与えます。そしてy_predは(None, 10)のshapeで「10個のクラスに属する確率」を表しているとします。

import tensorflow.keras.backend as K
from keras.objectives import categorical_crossentropy

def loss_function_category_soft(y_true, y_pred):
    # 2(鳥)～7（馬）までは天然物、それ以外は人工物
    # 天然物かどうかの確率
    prob_natural_pred = K.expand_dims(K.sum(y_pred[:, 2:8], axis=-1))
    # 人工物かどうかの確率
    prob_artificial_pred = 1-prob_natural_pred
    # 結合
    category_pred = K.concatenate([prob_natural_pred, prob_artificial_pred], axis=-1)
    # 真の値
    category_true = y_true[:, 10:]
    # カテゴリー別交差エントロピー＋クラス別交差エントロピー
    return categorical_crossentropy(category_true, category_pred) + categorical_crossentropy(y_true[:, :10], y_pred)

これはソフトマックスの値を天然物のクラス、人工物のクラスで和をとり、それらの交差エントロピーを取っています。例えばクラス別に、飛行機である確率が0.6、船である確率が0.2、鳥である確率が0.2であると推定されたら、天然物の確率は0.2、人工物の確率は0.8となります。

ハードマックス版

一方でソフトマックスに対応してハードマックス版も定義してみました。ソフトマックスとの違いは天然物、人工物のクラスの確率を0,1で推定することです。同じ例で飛行機である確率が0.6、船である確率が0.2、鳥である確率が0.2であると推定されたら、天然物の確率は0、人工物の確率は1と推定されます（真の値だけではなく推定値も0,1になるのがハードマックス版の特徴です）。

def loss_function_category(y_true, y_pred):
    ## ハードマックスになってる
    # 2(鳥)～7（馬）までは天然物、それ以外は人工物
    label_pred = K.expand_dims(K.argmax(y_pred))
    # 天然物かどうか
    is_natural_pred = K.cast(K.greater_equal(label_pred, 2) & K.less_equal(label_pred, 7), "float32")
    # 人工物かどうか
    is_artificial_pred = 1-is_natural_pred
    # 結合
    category_pred = K.concatenate([is_natural_pred, is_artificial_pred], axis=-1)
    # 真の値
    category_true = y_true[:, 10:]
    # カテゴリー別交差エントロピー＋クラス別交差エントロピー
    return categorical_crossentropy(category_true, category_pred) + categorical_crossentropy(y_true[:, :10], y_pred)

組み合わせ的に多数つなげたソフトマックス

実は人工物か天然物かどうかというのは、機械的に見れば『インデックスの「2以上7以下」に属するクラスの和を取れ』にほかならないので、インデックスの位置を変えて組み合わせ的にソフトマックスの損失関数をつなげることができます。

この場合はshapeを変えて、y_true, y_predも同じ(None, 10)というshapeとします。通常の10クラス分類と同じshapeです。

from itertools import combinations

def loss_function_category_soft_multi(y_true, y_pred):
    # まずはカテゴリー別の交差エントロピー
    loss = categorical_crossentropy(y_true, y_pred)
    # 10C2で起点と終点を選ぶ
    for comb in combinations(range(10), 2):
        probs_pred = K.expand_dims(K.sum(y_pred[:, comb[0]:(comb[1]+1)], axis=-1)) + K.epsilon()
        probs_true = K.expand_dims(K.sum(y_true[:, comb[0]:(comb[1]+1)], axis=-1)) + K.epsilon()
        loss += categorical_crossentropy(probs_true, probs_pred)
    return loss

2以上7以下以外のパターンで『天然物かどうか』のような人間にも理解できる意味付けをするのは難しいですが、これも確認してみましょう。

本来は他の損失関数でもK.epsilon()を足すべきでしょうが、これの関数で訓練させると交差エントロピーの過程でlog(0)を計算してしまいNanが発生するので、K.epsilon()を足しました。

実験設定＆コード

いま3つの種類の損失関数がありました。これに加えて、学習率を変えて通常の10クラス分類を2つやっています。これは学習のブーストが学習率を増やしたこととは異なるというのを示すためです。つまり以下の5パターンができます。

天然物か人工物かどうかを入れる・ハードマックス版（Natural HardMax）
天然物か人工物かどうかを入れる・ソフトマックス版（Natural SoftMax）
組み合わせ的に多数ソフトマックスの関数をつなげる（Multiple Softmax CrossEntropy）
通常の10クラス分類＋学習率1e-3（Normal label only(lr=1e-3)）
通常の10クラス分類＋学習率1e-2（Normal label only(lr=1e-2)）

オプティマイザーは全てAdamを使い、学習率は1～4は1e-3、5だけ1e-2としました。学習率の減衰はさせません。

損失関数が異なると同一の評価ができないので、いずれの場合もクラス間の精度を共通の指標（keras.metrics.categorical_accuracy）として入れています。y_true, y_predのshapeが異なる場合は、最初の10個で判定しています。これらは全てクラス別の推定確率を表します。最も良かったValidation accuracyはこの評価関数で計算しています（個々の異なる損失関数では見ませんがだいたい連動します）。

各パターン5回ずつ、1回100エポック、バッチサイズは512とし、TPUで学習させました。

コードは、ケース1～2＋4～5がこちら↓
https://gist.github.com/koshian2/0f854a040402f5ac4ba19c4b9a5abdbc
ケース3はこちらになります↓
https://gist.github.com/koshian2/8cb98ddac404be6c69b71b3217bd24c9

モデル

以下のコードでモデルを作ります。以前書いた10層の畳み込みニューラルネットワークでCIFAR-10のValidation Accuracy9割を達成するのネットワーク構造とほぼ同じです。10層です。

from tensorflow.keras.layers import Conv2D, BatchNormalization, Activation, Input, GlobalAveragePooling2D, AveragePooling2D, Dense
from tensorflow.keras.models import Model

def create_basic_block(input, filter, reps):
    x = input
    for i in range(reps):
        x = Conv2D(filter, 3, padding="same")(x)
        x = BatchNormalization()(x)
        x = Activation("relu")(x)
    return x

def create_model():
    input = Input((32, 32, 3))
    x = create_basic_block(input, 64, 3)
    x = AveragePooling2D(2)(x)
    x = create_basic_block(x, 128, 3)
    x = AveragePooling2D(2)(x)
    x = create_basic_block(x, 256, 3)
    x = GlobalAveragePooling2D()(x)
    x = Dense(10, activation="softmax")(x)

    model = Model(input, x)
    return model

結果

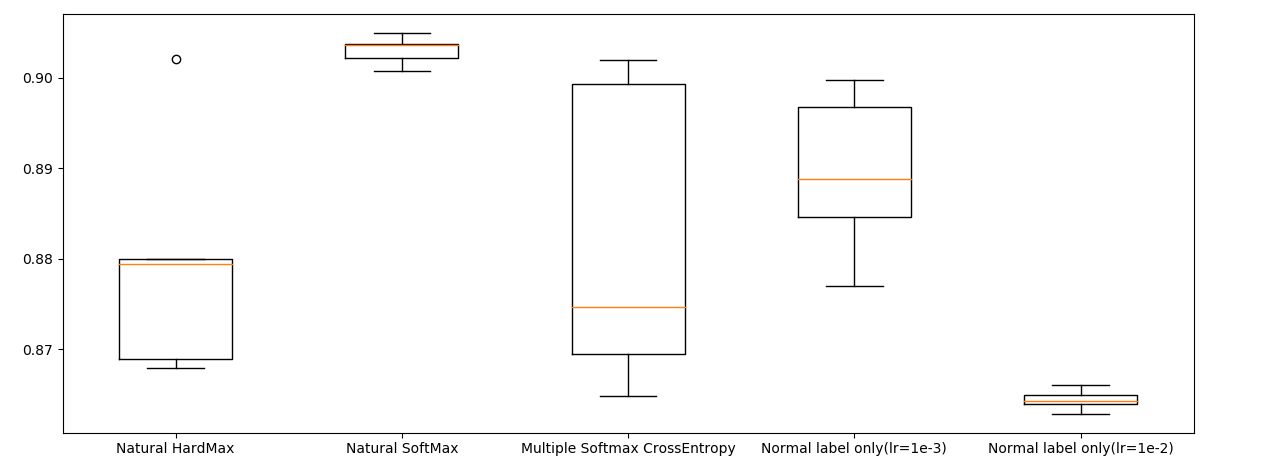
箱ひげ図でプロットしてみました。全て同一の評価関数：categorical_acuuracyの最大値を表しています。

2番目の「Natural SoftMax」が安定して強く、安定して9割オーバーできています。通常の損失関数：4番目「Normal label only(lr=1e-3)」はほどほどという結果になりました。また、損失関数の変更による収束性の向上は学習率の増加では説明できなく、4番目の学習率を10倍にした5番目の「Normal label only(lr=1e-2)」では学習率を増加させる前と比べて結果が悪化するという結果になりました。1番目のハードマックス関数はダメダメですね。

しかし、何でもかんでも損失関数に突っ込めばよいというわけではなく、組み合わせ的に総当たり的に追加した3番目の「Multiple Softmax CrossEntropy」ではただ精度の振れ幅が大きくなったという結果になりました。ここは慎重に検討する必要はありますが、直感的には「天然物か人工物か」のように意味ある区分でないと、精度の向上に寄与しないのではないかなと思います³。

「天然物か人工物かどうか」のフラグの有無でもう10回試行

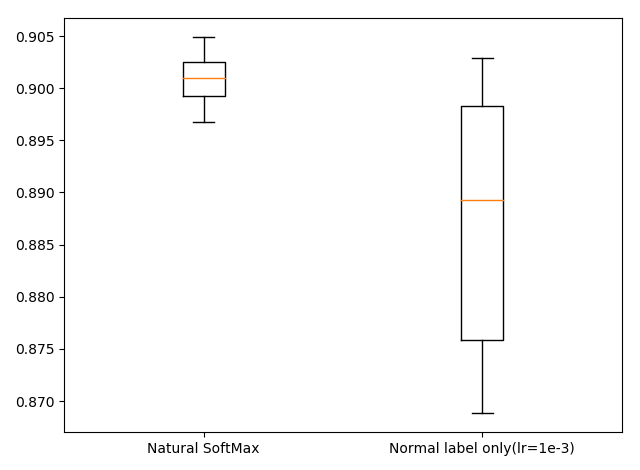
さて、5回程度では本当に意味があるか疑問なので、2番目のNatural SoftMaxと、4番目のNormal label only(lr=1e-3)だけもう10回試行し、累計15回の箱ひげ図を書いてみました。

確かにこれは効いてそう。ただブースト効果は精度で1～2%程度なので、ランドマーク検出ほどではなさそう。でもCIFAR-10を1～2%改善したぐらいで論文になるので、そこそこ意味あるかもしれない。

学習の経過を見る

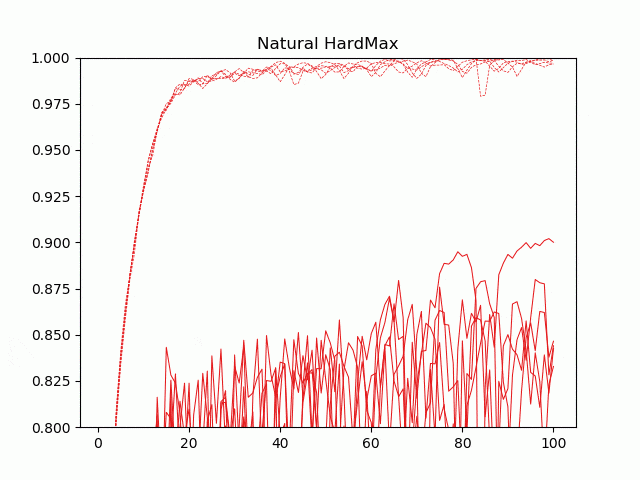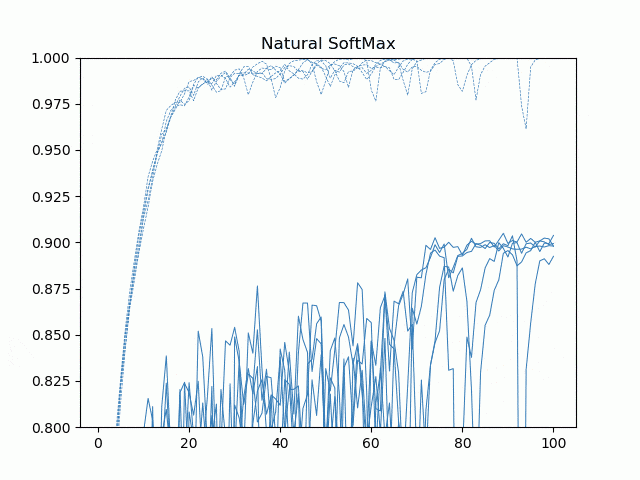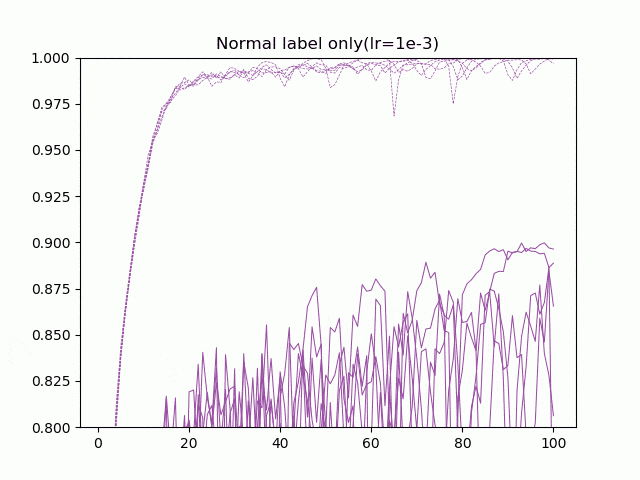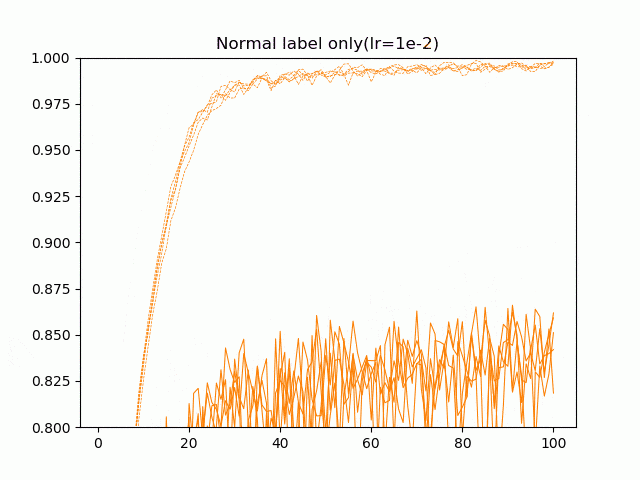
5ケース、5回づつの学習の経過を動画にしてみました。点線が訓練精度で、実線がテスト（交差検証）精度です。

Natural SoftMaxがとりわけ学習が速いというわけではないですが、最後のエポックあたりの収束がいいですね。

追記（11/10）：この記事と同日にほとんど同じアイディアの論文が投稿されてた

後で指摘されて知ったのですが、この記事を書いたのが11/8で、同日に投稿されたarXivでほとんど同じアイディアの論文があったそうです（ゲートを使っているのが若干違う）。この著者の方も初めて知りました（ケープタウン大学の方だそうです）。

ExGate: Externally Controlled Gating for Feature-based Attention in Artificial Neural Networks
https://arxiv.org/pdf/1811.03403.pdf

画像は論文より。日付も同じってさすがに笑いました。珍しいこともあるんですね。教えてくださった方ありがとうございました。

まとめ

効果としては正直なんともいえないところはありますが、どうやら分類問題でも損失関数を変えて訓練すると気持ち収束が良くなりそう結果が確認できました。ここではCIFAR-10に対して「天然物か人工物かどうか」という弱いラベルを与えてあげることで収束を良くしています。

他の研究の中での位置づけは、先程書いたStructured LearningやStructured Boostingの他に、階層分類、物体検出でよく使われるマルチタスク学習、弱教師あり学習（例えばこちら：誤ったラベルから正しいラベル分類を学習する弱教師あり学習）が近いのではないかなと思います。

「天然物か人工物かどうか」というのが弱い分類器だとすれば、これはもしかするとアンサンブル学習のような挙動をしているのかもしれません。ここらへんを総合的に扱った論文というのは自分は見たことないですし、あまり注目されていないのかもしれません。ただ、「分類問題の損失関数はクラス単位でのCategorical Crossentropyでなければならない」なんて決まりは1つもないので、皆さんの思い込みを捨てるきっかけとなれば幸いです。

これはメリットもあればデメリットもあると思います。だまし絵のような「錯視」も広い意味で見れば、このような先入観が働いているから起こり得るのではないでしょうか。 ↩
さすがにこれは研究されているだろうと思ったらありました。似た研究で「Structured Boosting」や「Structured Learning」などで検索すると出てきます。 ↩
ランドマーク検出では総当たりで組み合わせを投入したらうまく言ったのに、分類ではうまくいかないの？という疑問は、おそらくですがランドマーク検出では組み合わせ的に投入することが、ランドマーク全体の形状を規定しているため、全体として意味のある区分となったのではないかと思います。分類問題の場合は組み合わせ的に交差エントロピーを投入しても、全く説明力のない組み合わせはほぼノイズとなってしまったのでしょう。 ↩