猫の顔のランドマーク検出をやってみました。ただのランドマーク検出のつもりでしたが、MSEと同一の最適解で別の側面からの魔改造した損失関数を投入すると学習を明らかにブーストできる(損失がMSEベースで1/5になる)ことに気づいたので、それがメインになっています。
今回はこれに加えて、ResNet-50から転移学習させ、Google ColabのTPUで訓練させました。
リポジトリ:https://github.com/koshian2/cats-face-landmarks
学習済み係数は一番最後のケース7の損失関数を使って訓練させたものです。
ランドマーク検出とは
画像から要所要所となる点(ランドマーク)を検出するアルゴリズム。顔なら、目、鼻、口、眉毛、輪郭といったポイントを検出します。例としてはOpenCVによる実装があります。

(https://docs.opencv.org/3.4/d2/d42/tutorial_face_landmark_detection_in_an_image.htmlより)
ディープラーニングでもランドマーク検出はできる
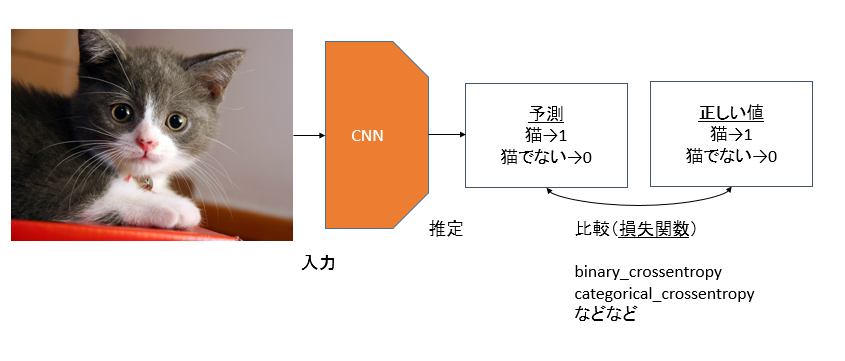
OpenCVの実装をよく理解していないのでOpenCVのランドマーク検出はよくわかりませんが、ディープラーニングでのランドマーク検出自体は結構単純です。例えば、ディープラーニングで猫を分類しようとすると、
このようにCNN(畳み込みニューラルネットワーク)を通して1、「猫か猫でないか」を判定します。ここでのポイントは損失関数です。今回の7,8割は損失関数がテーマです。
分類の場合は、猫かどうかというクラスを予測し、「binary_crossentropy」や「categorical_crossentropy」といった損失関数を使います。これを少し変えるとランドマーク検出ができます。
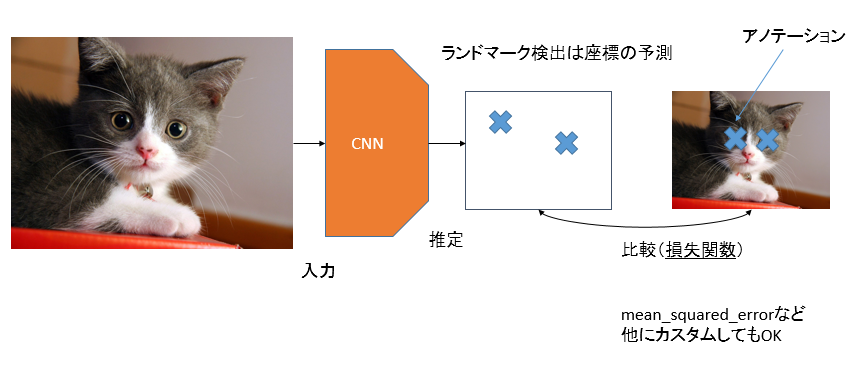
ランドマーク検出の場合は、例えば目をランドマーク(検出したいポイント)とするなら、予測するのは目の座標です。損失関数は例えばmean_squared_errorを使います(後述しますがこれをカスタムしてもいいです)。どちらかというとニューラルネットワークを使った回帰問題に似てきますね。
ちなみに物体検出を含め、ランドマーク検出では「アノテーション」という用語をよく使います。これはランドマーク検出では、目、鼻、口といったランドマークの座標を表します。分類問題のラベルとほぼ同じ意味合いと捉えていいと思います。
Cat Dataset
KaggleにCat Datasetという猫の画像だけ9000枚以上集めたデータセットがあります(CC0:Public Domain)。これには左目、右目、口、左耳3ヶ所、右耳3ヶ所の計9ヶ所のxy座標でのアノテーションが付属しています。
このようなイメージですね。
モデル
今回はResNet-50を転移学習させます。以下のような構成です。
- 入力:(224, 224, 3)
- ResNet-50 : 82番目のレイヤー(res4a_branch2a)から訓練させる
- 出力ユニットは18個, シグモイド関数
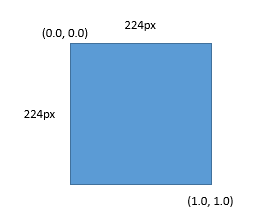
そして座標系を設定しておきましょう。今回は画像の左上の点を(0,0)、右下を(1,1)とします。こうしておくと画像をリサイズしたときのアノテーション変換がやりやすくなります。
データセットを作る
データの整形の部分を軽く。
アノテーションの整形
アノテーションがファイル単位で格納されていますが、これだとちょっとやりづらいのでアノテーション全体を1つのファイルにまとめます。画像ファイルを読み出すたびにアノテーションが必要になるので、Dictionary形式に格納してメモリに置いておくのが良いかと思います。これを漬物化しました。コードはこちら。
これから作るデータセットのルートディレクトリを「cats-dataset」としたら、そのフォルダの直下に「cat_annotation.dat」をおいておきます。
訓練:テストの分割
元のデータセットでは訓練とテストデータがごっちゃになっているので、7:3で分割します。全体で9995枚データがあったので、訓練=6996枚、テスト=2999枚となりました。コードはこちら。sklearnのtrain_test_splitでサクッとやりましょう。
tar.gzに詰めてTPUで訓練
あとはGoogle Colabで扱いやすいようにtar.gzで詰めます。コードは書くまでもないけどこちら。
あとはこのファイルをGoogle DriveにアップロードしてColabで読み込ませれば訓練できます。サイズは2GB弱です。
訓練の際は学習率1e-3、係数0.9のモメンタムオプティマイザーを使い、バッチサイズは512としました。
ジェネレーター
ランドマーク検出はジェネレータが若干面倒くさいです。特にData Augmentationする場合は気をつけましょう。
class CatGenerator:
def __init__(self):
with open("cats-dataset/cat_annotation.dat", "rb") as fp:
self.annotation_data = pickle.load(fp)
def flow_from_directory(self, batch_size, train=True, shuffle=True, use_data_augmentation=True):
source_dir = "cats-dataset/train" if train else "cats-dataset/test"
images = glob.glob(source_dir+"/*.jpg")
X_cache, y_cache = [], []
while True:
if shuffle:
np.random.shuffle(images)
for img_path in images:
with Image.open(img_path) as img:
width, height = img.size
img_array = np.asarray(img.resize((224, 224), Image.BILINEAR))
basename = os.path.basename(img_path)
data = self.annotation_data[basename]
# アノテーションを0~1に変換
annotation = np.zeros((9,2), dtype=np.float32)
annotation[:, 0] = data[2][:, 0] / width
annotation[:, 1] = data[2][:, 1] / height
annotation = np.clip(annotation, 0.0, 1.0)
if train and use_data_augmentation:
# 水平反転
if random.random() >= 0.5:
img_array = img_array[:, ::-1, :]
annotation[:, 0] = 1 - annotation[:, 0]
# 左目と右目の反転
annotation[0, :], annotation[1, :] = annotation[1, :], annotation[0, :].copy()
# 左耳と右耳の反転
annotation[3:6, :], annotation[6:9, :] = annotation[6:9, :], annotation[3:6, :].copy()
# PCA Color Augmentation
img_array = self.pca_color_augmentation(img_array)
X_cache.append(img_array)
y_cache.append(np.ravel(annotation))
if len(X_cache) == batch_size:
X_batch = np.asarray(X_cache, dtype=np.float32) / 255.0
y_batch = np.asarray(y_cache, dtype=np.float32)
X_cache, y_cache = [], []
yield X_batch, y_batch
def pca_color_augmentation(self, image_array_input):
assert image_array_input.ndim == 3 and image_array_input.shape[2] == 3
assert image_array_input.dtype == np.uint8
img = image_array_input.reshape(-1, 3).astype(np.float32)
img = (img - np.mean(img, axis=0)) / np.std(img, axis=0)
cov = np.cov(img, rowvar=False)
lambd_eigen_value, p_eigen_vector = np.linalg.eig(cov)
rand = np.random.randn(3) * 0.1
delta = np.dot(p_eigen_vector, rand*lambd_eigen_value)
delta = (delta * 255.0).astype(np.int32)[np.newaxis, np.newaxis, :]
img_out = np.clip(image_array_input + delta, 0, 255).astype(np.uint8)
return img_out
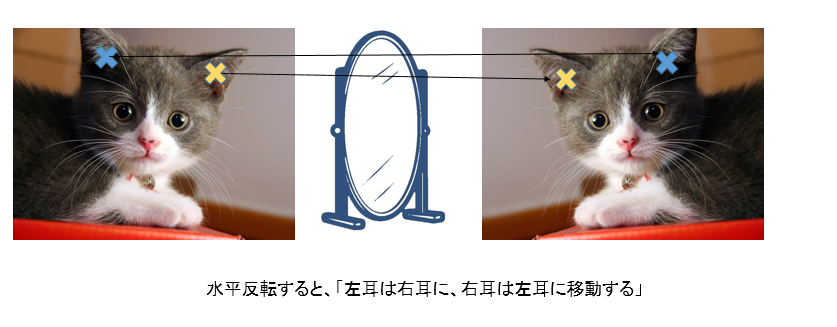
詳しくは別の記事で書きました2が、例えば画像を水平反転させるときは$x\to 1-x$とアノテーションの座標の反転だけではなく、ちゃんと意味的な反転もしないといけません。
画像の水平反転とは、画像の右端に鏡をおいてそれの鏡像を取り出すのと同じなので、水平反転すると鏡像では左耳は右耳に、右耳は左耳に移動します。これをちゃんと抑えないと誤差が綺麗に収束しません。
ジェネレーターでPCA Color Augmentationを定義していますが3、これは後の最後のパターンでしか使いません。
損失関数試行錯誤
Google ColabのTPUで訓練させました。訓練コードはこちらから。損失関数を若干変えています。PCA Color Augmentationがちょっと重いですが、これ使わなければTPUで6時間ぐらいで訓練できました。
1. 通常のMSE(Mean Squared Error)
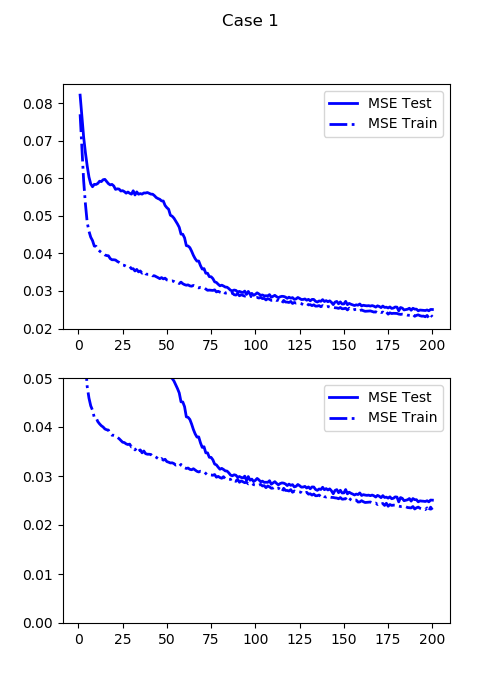
まずは普通のMSEから。200エポック訓練させました。
from keras.objectives import mean_squared_error
def loss_function_simple(y_true, y_pred):
return mean_squared_error(y_true, y_pred)
最小テスト損失:0.024716419354081153
これからプロットする画像は全てテスト(交差検証)画像です。まだ全然エラー大きいです。もうちょっと訓練させてみましょう。
2. 通常のMSE・400エポック
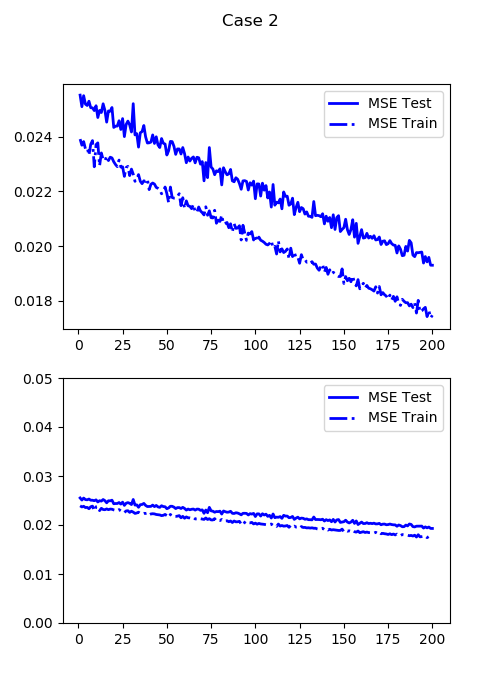
1の倍訓練させました。200エポックからのスタートです。
最小テスト損失:0.019296562671661376
多少数字は落ちたものの、あんまり改善していません。落ち方が遅すぎます。なんというか出てきたランドマークがボヤっとしていますよね。
3. MSE+1次の差分距離
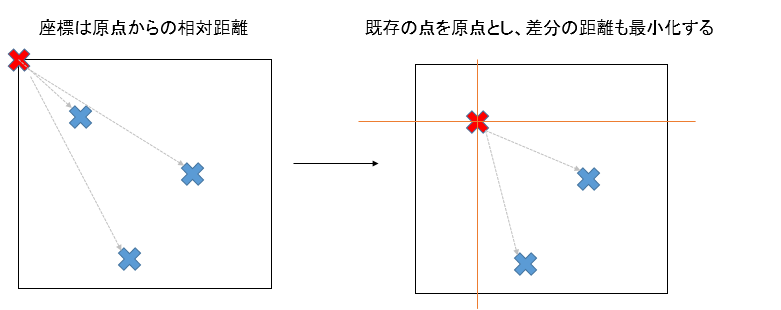
ここで損失関数に距離の概念を入れます。そもそも座標とは原点を基準とした相対的な距離なのです。
つまり、発想の転換で、既存のランドマーク1点を選択してそこを基準にした差分の座標(距離)も損失関数に放り込んでしまえばいいのです。
数式で書いてみましょう。あるアノテーション$a_i(1\leq i\leq N)$に対する平均二乗誤差(MSE)を、
$$MSE(a_i)=\frac{(a_{i,x}^{TRUE}-a_{i,x}^{PRED})^2+(a_{i,y}^{TRUE}-a_{i,y}^{PRED})^2}{2} $$
とします。ここで$a_{i,x}$はアノテーション$a_i$の$x$座標、$a_{i,y}$は$y$座標を表します。また$a_i^{TRUE}$は$a_i$の真の座標、$a_i^{PRED}$は座標の予測値を表します。
(1)の通常のMSEを式で表すと、
$$MSE(a_1, \cdots, a_i, \cdots, a_N)=\frac{MSE(a_1)+\cdots+MSE(a_i)+\cdots+MSE(a_N)}{N}=DDMSE(0)$$
となります。またこれは0次の差分距離なので、$DDMSE(0)$と表すことにします。
1次の差分距離とはこうです。
\begin{align}
DDMSE(1) &= MSE(a_2-a_1, \cdots, a_i-a_{i-1}, \cdots, a_N-a_{N-1}) \\
&= \frac{MSE(a_2-a_1)+\cdots+MSE(a_i-a_{i-1})+\cdots+MSE(a_N-a_{N-1})}{N-1}
\end{align}
つまりここでの損失関数は次のようになります。
$LOSS_3=DDMSE(0)+DDMSE(1)$
これをコードで書くと次のようになります。
def loss_function_with_distance(y_true, y_pred):
point_mse = mean_squared_error(y_true, y_pred)
distance_mse = mean_squared_error(y_true[:, 2:18]-y_true[:, 0:16], y_pred[:, 2:18]-y_pred[:, 0:16])
return point_mse + distance_mse
この式が完全に最小化されるとき、全てのアノテーションの予測値は真の値と一致します。しかし、$DDMSE(0)$のみのとき(1,2)と大きな違いは、より大きな勾配が得られるということです。差分距離という「距離」の情報を与えてやることで、ニューラルネットワークがより最適解に向かって進みやすくなるようにサポートしてあげるのです。事実、これはうまくいきます。
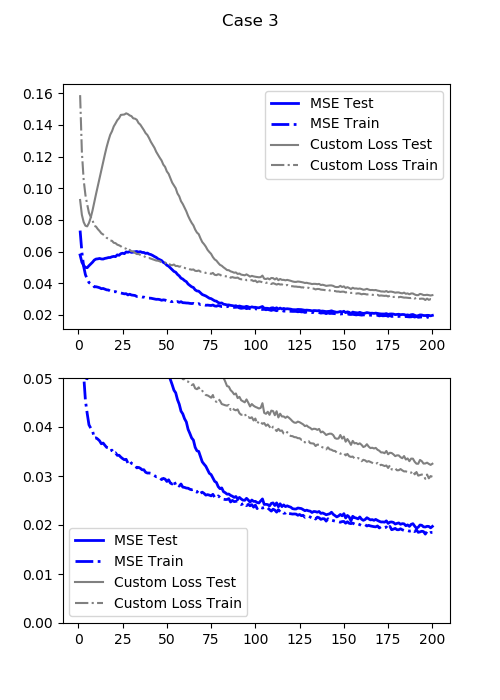
最小テスト損失(通常のMSE:DDMSE(0)):0.01942022442817688
この損失関数($LOSS_3$)での最小テスト損失:0.0322693221271038
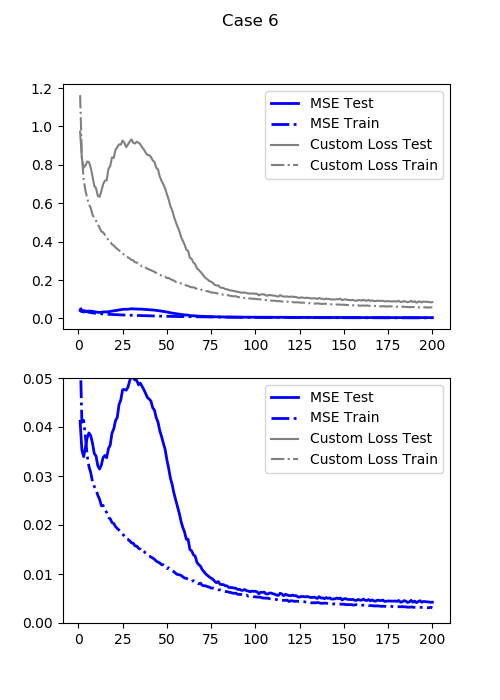
たった200エポックで、通常のMSEの場合で400エポックかかったのとほぼ同じ精度まで行くことができました。ちなみに、損失関数を変えると異なるケースで同一の評価ができないので、通常のMSE(DDMSE(0))を評価関数として導入しています(グラフの青線)。グラフを見てわかるように、$LOSS_3$と通常のMSEの最小化はほぼ同じです。異なるのは勾配をより得られやすくなるということです。ちなみにこれは通常のMSEで学習率を大きくしたのでは実現できませんでした。
出てきた画像を見るとモヤッとした印象は抜けて顔っぽい形になってきました。
まだまだ続きます。
4. 多次の差分距離
3で1次の差分距離を追加したということは、組み合わせ的に(全ての点-1)を基準とした差分距離を追加できるというわけです。アノテーションの数$N=3$なら、まず原点を基準とした通常のMSE、DDMSE(0)が3点分、1番目の点を基準としたDDMSE(1)が2点分、2番目の点を基準としたDDMSE(2)が1点分、計6点分得られるようになります。
次の式で定義します。
$$LOSS_4 = DDMSE(0)+DDMSE(1)+\cdots+DDMSE(N-1)$$
コードで書くと次のとおりです。
def loss_function_with_multiple_distance(y_true, y_pred):
error = mean_squared_error(y_true, y_pred)
for i in range(8):
error += mean_squared_error(y_true[:, ((i+1)*2):18]-y_true[:, 0:(16-i*2)], y_pred[:, ((i+1)*2):18]-y_pred[:, 0:(16-i*2)])
return error
つまり、通常のMSEでは$N$点分だけの情報でしたが、$\frac{N(N+1)}{2}$個分の距離の情報が得られるようになります。今回はアノテーションが9点だったので、9点から45点まで情報が増えます。これそこそこ効きます。
最小テスト損失(通常のMSE:DDMSE(0)):0.015157081373035907
この損失関数($LOSS_4$)での最小テスト損失:0.058822234719991685
同じ200エポックながら、通常のMSEの400から更に、200→400に相当する分の損失が減っています。ここでカスタマイズした損失関数はいびつながらも、通常のMSEとかなり連動しているのがわかります。なぜなら、通常のMSEとこの損失関数の最適解は一緒だからです。この差分距離がMSEによる損失関数をブーストしているのです。
それになんとなく顔の形っぽくなってきましたね。つまり、差分距離で雁字搦めにしてやることでより大きい勾配が得られるようになったと考えることができます。
5. 多次の差分距離+任意三角形の面積の損失(あんまうまくいかない)
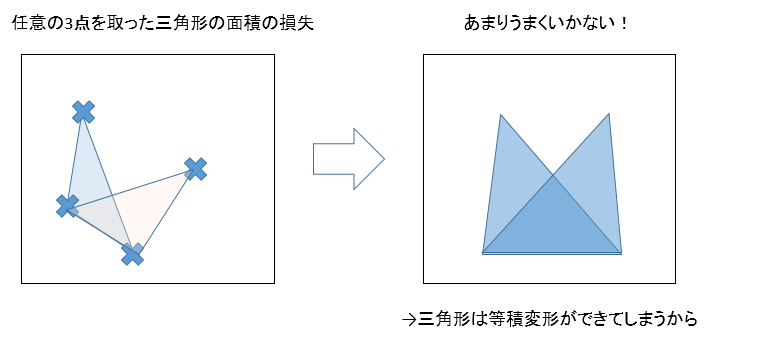
損失関数を魔改造していますが、多次の差分距離にくわえて2点から3点に比較基準を増やして任意の3点の面積も最小化してしまおうという魂胆です。確かに組み合わせが爆発的に増えれば縛りが増えてうまくいきそうな気がします。ただ、これはあんまりうまく行きません。
なぜなら三角形は等積変形ができてしまうからです。例えば右のようなケースを見ると、底辺は共通でも頂点を横にスライドさせれば同一の面積の三角形を作れてしまうからです。差分距離の場合は、ある2点を距離同じに移動させようとすると、他の点からの距離がガツンと増えてしまうのでこういう心配はないと思います4。
こんなコードです。サラスの公式を使っています。
# 三角形の面積を求める関数
def sarrus_formula(p1, p2, p3):
# 座標シフト
a = p2 - p1
b = p3 - p1
return K.abs(a[:,0]*b[:,1] - a[:,1]*b[:,0]) / 2.0
from itertools import combinations
def loss_function_multiple_distance_and_triangle(y_true, y_pred):
# 点損失
error = mean_squared_error(y_true, y_pred)
# 線の損失
for i in range(8):
error += mean_squared_error(y_true[:, ((i+1)*2):18]-y_true[:, 0:(16-i*2)], y_pred[:, ((i+1)*2):18]-y_pred[:, 0:(16-i*2)])
# 面の損失
for comb in combinations(range(9), 3):
s_true = sarrus_formula(
y_true[:, (comb[0]*2):(comb[0]*2+2)],
y_true[:, (comb[1]*2):(comb[1]*2+2)],
y_true[:, (comb[2]*2):(comb[2]*2+2)]
)
s_pred = sarrus_formula(
y_pred[:, (comb[0]*2):(comb[0]*2+2)],
y_pred[:, (comb[1]*2):(comb[1]*2+2)],
y_pred[:, (comb[2]*2):(comb[2]*2+2)]
)
error += K.abs(s_true - s_pred)
return error
この結果は以下のようになります。
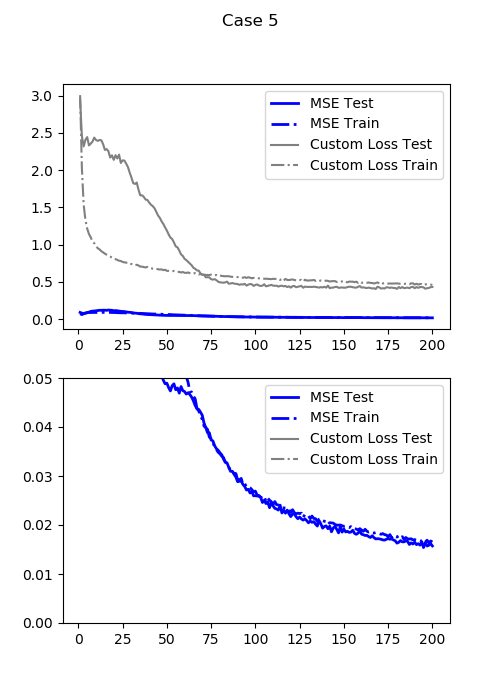
最小テスト損失(通常のMSE:DDMSE(0)):0.01715473271906376
この損失関数での最小テスト損失:0.40301419496536256
先程の多次の差分距離だけのよりは悪くなってしまいました。出力画像を見るとあんま良くなってませんよね。
というわけで三角形の面積は忘れてしまいましょう。
6. 多次の差分距離+パーツ別エリア損失
多次の差分距離の場合は、形状は再現できても、場所が異なるというようなケースがありました(例えば下の段の真ん中)。そのため、ある境界箱(エリア)を与えてその中のアノテーションが属しなければペナルティーを与えるというような処理を行います。今回は、右耳と左耳がそれぞれ3つのアノテーションからなるので、右耳と左耳でそれぞれエリアを計算して、それぞれペナルティーを作ります。
かなり面倒な数式の定義がありますがお付き合いください。面倒ならプログラムだけ見てください。今エリアが$M$個あるとしましょう。今回の例では右耳、左耳の2つのエリアからなるので$M=2$です。アノテーション$a_i(1\leq i\leq N)$が、エリア$B_j(1\leq j \leq M)$に属することを、$a_i\in B_j$と表現します。各エリアの左上の座標を$(b_{j, x, min}, b_{j, y, min})$、右下の座標を$(b_{j, x, max}, b_{j, y, max})$とします。各点の求め方は、
\begin{align}
b_{j, x, min} &= \min_{i=1\to N, a_i\in B_j}a_{i, x} \\
b_{j, y, min} &= \min_{i=1\to N, a_i\in B_j}a_{i, y} \\
b_{j, x, max} &= \max_{i=1\to N, a_i\in B_j}a_{i, x} \\
b_{j, y, max} &= \max_{i=1\to N, a_i\in B_j}a_{i, y} \\
\end{align}
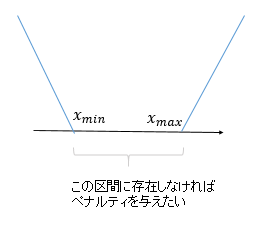
次にペナルティーの関数を考えます。x,y座標は直交化できるので、わかりやすいように1次元で考えます。変数$x$に対して、図のように$x_{min}$から$x_{max}$の間に属さない場合のペナルティーを次のようにします。
$$p(x_{min}^{pred}, x_{max}^{pred}|x_{min}^{true}, x_{max}^{true}) = \max(x_{min}^{true}-x_{min}^{pred}, 0)+\max(x_{max}^{pred}-x_{max}^{true},0) $$
ちょうどサポートベクターマシンのHingeロスみたいな感じですね。したがって、エリア$B_j$の損失$AL_j$は次のようになります。
$$AL_j = \frac{1}{n_j}\sum_{i=1, a_i\in B_j}^N \bigl[ p(b_{j, x, min}^{pred}, b_{j, x, max}^{pred}|b_{j, x, min}^{true}, b_{j, x, max}^{true}) + p(b_{j, y, min}^{pred}, b_{j, y, max}^{pred}|b_{j, y, min}^{true}, b_{j, y, max}^{true})\bigr] $$
ここで$n_j$はエリア$B_j$に属するサンプルの数です($2\leq n_j\leq M, n_1+\cdots+n_j+\cdots+n_M=N$)。もし$n_j$が0なら$AL_j$は0とします。全体のエリア損失はこれらの和です。全体のエリア損失を$AL$とすれば、
$$AL = AL_1 + \cdots + AL_j + \cdots + AL_M $$
となります。そして新しい損失関数$LOSS_6$を次のように定義します。
$$LOSS_6 = LOSS_4 + AL = \sum_{i=0}^{N-1}DDMSE(i) + \sum_{j=1}^M AL_j $$
数式で書くとものすごいわかりづらいですが、プログラムを見ると別にそこまで難しくないです。
def calc_area_loss(ear_true, ear_pred):
left_x = K.expand_dims(K.min(ear_true[:, ::2], axis=-1))
left_y = K.expand_dims(K.min(ear_true[:, 1::2], axis=-1))
right_x = K.expand_dims(K.max(ear_true[:, ::2], axis=-1))
right_y = K.expand_dims(K.max(ear_true[:, 1::2], axis=-1))
# 予測のX,y
pred_x = ear_pred[:, ::2]
pred_y = ear_pred[:, 1::2]
# ペナルティ
penalty_x = K.maximum(left_x - pred_x, 0.0) + K.maximum(pred_x - right_x, 0.0)
penalty_y = K.maximum(left_y - pred_y, 0.0) + K.maximum(pred_y - right_y, 0.0)
return K.mean(penalty_x + penalty_y, axis=-1)
def loss_function_multiple_distance_and_area(y_true, y_pred):
# 点損失
error = mean_squared_error(y_true, y_pred)
# 線の損失
for i in range(8):
error += mean_squared_error(y_true[:, ((i+1)*2):18]-y_true[:, 0:(16-i*2)], y_pred[:, ((i+1)*2):18]-y_pred[:, 0:(16-i*2)])
# 右耳と左耳のエリア
left_ear_true, left_ear_pred = y_true[:, 6:12], y_pred[:, 6:12]
right_ear_true, right_ear_pred = y_true[:, 12:18], y_pred[:, 12:18]
error += calc_area_loss(left_ear_true, left_ear_pred)
error += calc_area_loss(right_ear_true, right_ear_pred)
return error
calc_area_lossがエリア損失ですね。ここでは右耳と左耳のエリア損失をつけています。それに多次の差分距離を足しているだけです。数式で見ると非常にごちゃごちゃしてますが、これがめちゃくちゃ効きます。
最小テスト損失(通常のMSE:DDMSE(0)):0.004149417951703071
この損失関数($LOSS_6$)での最小テスト損失:0.08219061940908431
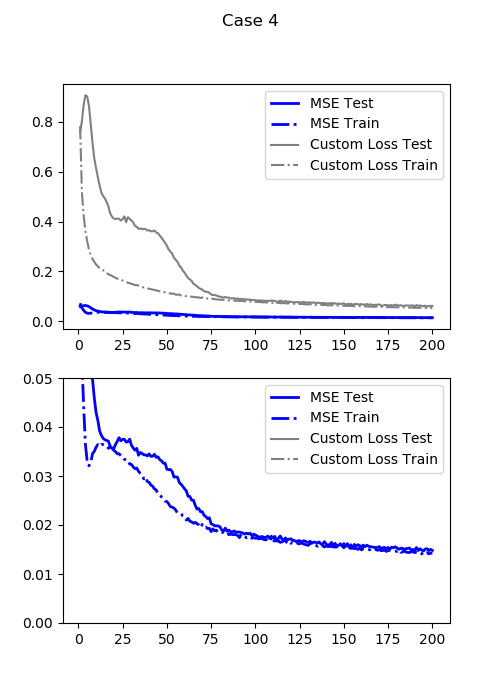
ケース4が0.0152だったの対して、今回は0.0041と損失が約1/4になりました。しかも同じ200エポックしか回していません。むちゃくちゃ強いです。
かなり自然な感じになってきました。エリア損失を導入することで、場所もだいたい合うようになっています。
7.多次の差分距離+パーツ別エリア損失+PCA Color Augmentation
最後に若干オーバーフィッティングしているので、PCA Color Augmentationで味付けします。6以前はこのAugmentationを使っていません。
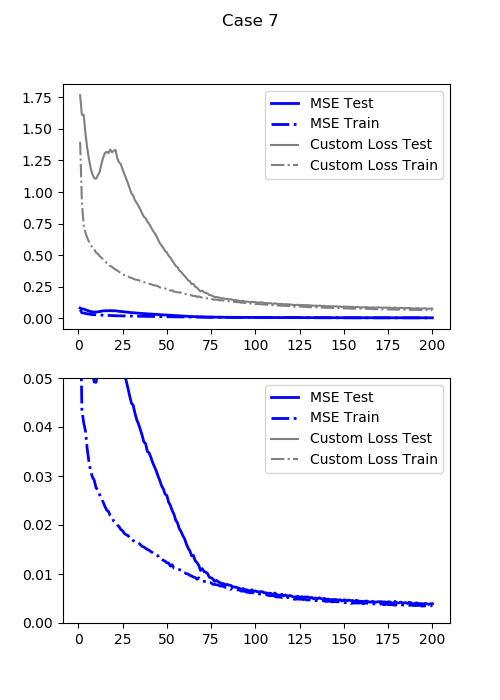
最小テスト損失(通常のMSE:DDMSE(0)):0.003793809376657009
この損失関数($LOSS_6$)での最小テスト損失:0.07437080889940262
損失関数は6と同一です。若干(1割程度)テスト損失が小さくなりました。
アイディアが尽きたのでこれで終わりです。
新しい画像を試してみる
訓練にも交差検証にも全く使っていない新しい画像を試してみます。
おっ、なかなかいいですね。ちょっと口のあたりがずれていますが、ResNet-50でも十分猫のランドマーク検出ができました。
ケース別比較
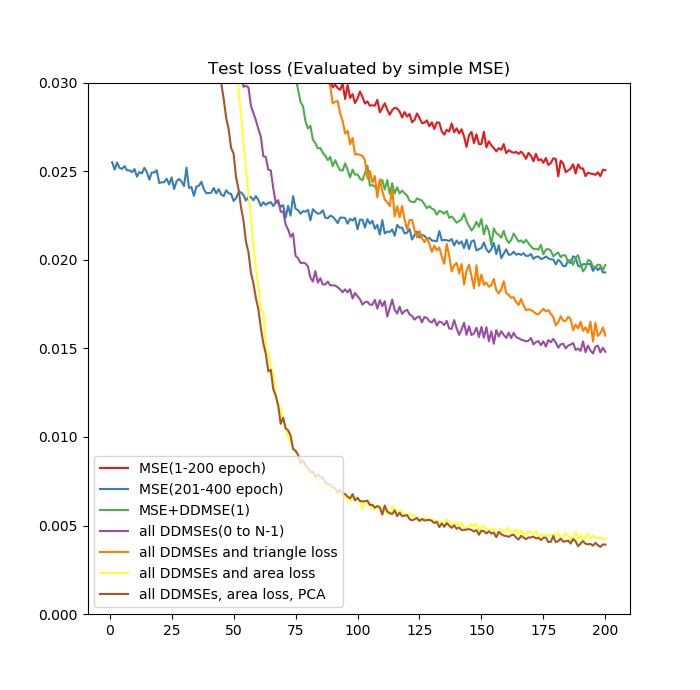
さて、各損失関数でどれぐらいよくなったのか通常のMSEを基準に比較してみましょう。
損失関数を変えるだけで損失が1/5ぐらいになったことを確認できました。
差分距離とエリア損失がよく効いているのが確認できました。
なぜうまく行くか
このような損失関数がうまくいくのは確認できましたが、もう少し直感的な意味付けをしましょう。当たり前のように使われるMSEというのは、この言い方が正しいかどうかはわかりませんが、あくまで「点の」推定だからです。点ごとの差分距離やエリア損失といった複数の情報がある損失関数を使うことで、点だけではなく「線」や「面」、「パーツ」といったデータ(ここでは顔)の構造の情報が加わります。
まとめ
ディープラーニングによるランドマーク検出という他の分類問題に比べて具体例が少ないケースを取り扱いましたが、最適解がMSEと同一ながら差分距離やエリア損失といった別の側面からのカスタマイズ損失関数を適用することで、より大きな勾配を得ることができ、明らかに学習をブーストさせることが確認できました。
これは特に何かの論文を参照にしたわけではなく、自分の完全な思いつきですが、似たような研究があったらぜひ教えてください。もしかしたら、普通の分類問題もこのようなブースト用の損失関数を適用すると、もっと良い精度が得られるかもしれませんね。