2021年のディープラーニング論文を1人で読むAdvent Calendar最終日の記事です。ラストに読むのは物体検出の金字塔YOLOシリーズから2021年に発表された「YOLOX」です。
この論文は既に解説もいくつかあるので、論文をあまり読まずに公式コードの実装に注目します。公式コードの特に訓練時の損失計算に渡す前の部分を、簡単な数値サンプルを使ってゆっくりに見ます。これを見ることでYOLOXのキーアイディアである「アンカーフリー」「Multi Positives」「SimOTA」を理解していきたいと思います。
論文はカンファに採択されたものというよりも、CVPR2021の「Workshop on Autonomous Driving」というワークショップであったStreaming Perception Challengというコンペの1位の解法という扱いです。著者はメグビーのチームです。
自分はYOLOv1を読んだだけで、それ以外はちゃんと読んだことないただの物体検出素人なので、間違っている点あるかと思いますが、生暖かく見ていただければ幸いです。
- タイトル:YOLOX: Exceeding YOLO Series in 2021
- URL:https://arxiv.org/abs/2107.08430
- 出典:Zheng Ge, Songtao Liu, Feng Wang, Zeming Li, Jian Sun; arXiv:2107.08430 [cs.CV]
- コード:https://github.com/Megvii-BaseDetection/YOLOX
YOLOXはアンカーフリー
アンカーフリーではないYOLOは何?
YOLOXの大きな特徴としてアンカーフリーという点があります。そもそもアンカーフリーではないYOLOとは何でしょうか。YOLOXの論文では、YOLOv2やYOLOv3がアンカーがある例として紹介されていました。
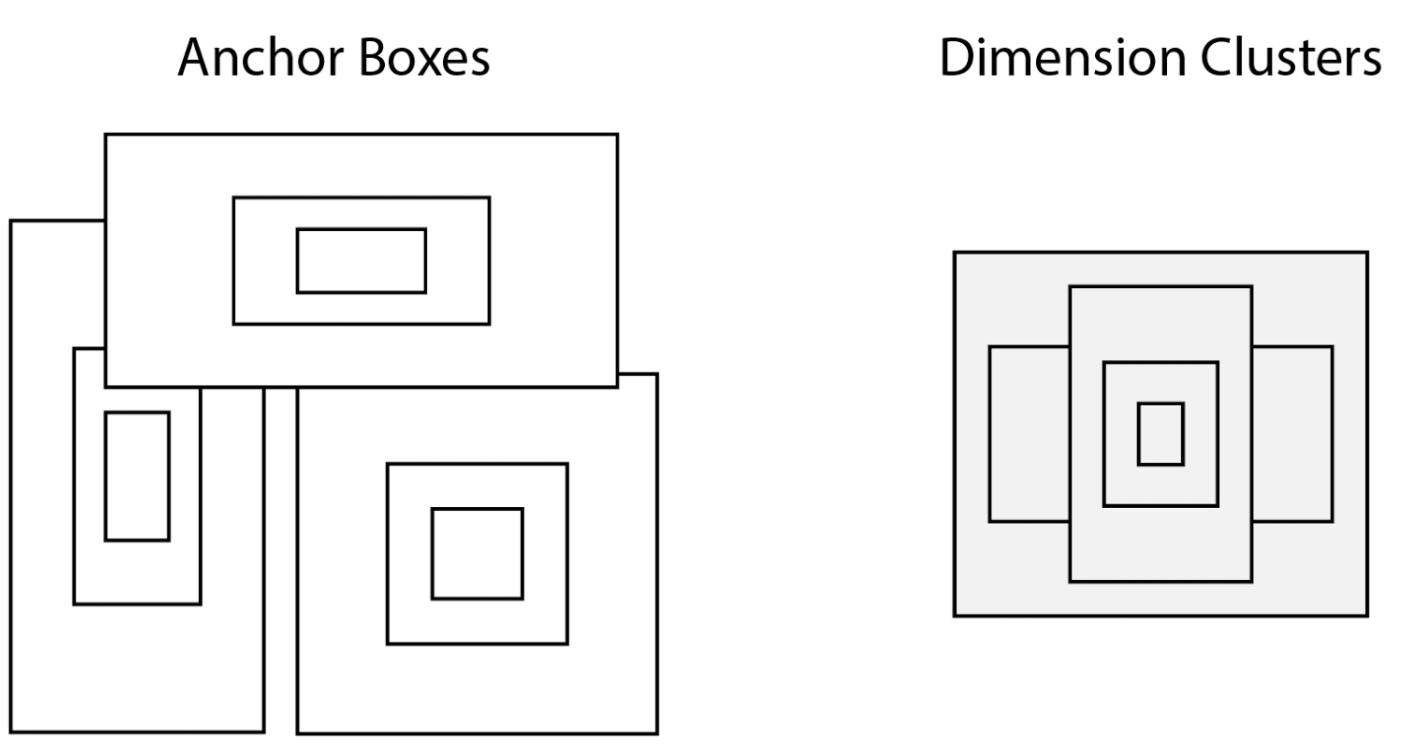
これはYOLOv2の公式サイトにあったスライドからの引用ですが、(YOLOv2の論文)
この左にある「Anchor Boxes」と書かれているものが通称:アンカーと呼ばれているものです。アンカーは中心が同じで、大きさが異なる四角形がいくつも描かれているのがわかります。
アンカーの起点は特徴マップの中心
そもそもこの中心はなにを意味するのか、というと特徴マップの中心点です。これはYOLOv1の公式サイトにあったスライドを編集したものです。(YOLOv1の論文)
右上の車を検出したいとしましょう。画像全体をもう少し小さいグリッドに分割して考えます。車の四角形(Bouding Box)の中心のあるグリッドが、車を検出する役割を担えばいいのです。
このグリッドはCNNの特徴マップに相当します。例えば画像の解像度が512×512で、CNNの途中で合計1/32倍にダウンサンプリングされたとしましょう。出力解像度は16×16になります。この16×16がそのままグリッドに相当します(この場合は32×32サイズのグリッドです)。CNNは位置不変性があるので、入力-出力の位置のアラインメントがとれます。
グリッド、すなわち特徴マップ上で、クラス分類とBounding Boxの大きさの回帰をマルチタスクで学習させたのが、YOLOの根幹思想です。YOLOとは「You Only Look Once」の略ですが、「グリッド単位で複数回推論しなくても、画像全体を1回推論させればいい」というのがこの英語の由来です。
アンカーフリー=特徴マップにつき1個のボックスにする
YOLOv2やv3に見られる、アンカーフリーではない(アンカーボックスが複数個ある)というのは、サイズの異なるボックスを1つの特徴マップからいくつも出ている状態です。これを特徴マップにつき1個のボックスに戻しましょう、というのがアンカーフリーのやりたいことです。
実はYOLOv1は1つの特徴マップにつきアンカーボックスが1個しかないので、アンカーフリーとみなすことができます。直感的にはYOLOv1のような仕組みに戻ったとも言えます。ただ、精度や速度はv1のそれを遥かにアウトパフォームしています。
特徴マップと画像の座標の対応
ダウンサンプリングの倍率をかける
物体検出では「今計算しているのがどこの座標系か」というのが問題になります。YOLOXの公式実装では、特徴マップ上の座標を入力画像の座標に対応させて計算しています。
例えば、1/32のダウンサンプリングを経て、元の解像度が512×512の画像が、16×16特徴量へマッピングされたものとしましょう。この特徴マップの1ピクセルは、元の画像の32×32に相当します。特徴マップの座標を0インデックスとしたとき、各ピクセルは元の画像では次の座標に対応します。
- $(i=0, j=0)$の左上の点→(0, 0)
- $(i=0, j=0)$の中心点→(15, 15)
- $(i=3, j=4)$の左上の点→(96, 128)
- $(i=5, j=2)$の中心点→(175, 79)
- $(i=1, j=2)$の右下の点→(63, 95)
ピクセルの左上・中央・右下の点というのは、ピクセル本来の意味からは考えられませんが、元のスケール(座標)に戻せば考えられます。
座標対応の計算から、損失関数までつなげるのがYOLOの難しいところなので、YOLOXの公式実装を使い簡単な数値例で追っていきます。
これからYOLOXの実装を細かく見ていきますが、ほとんどHeadの部分、訓練時の損失関数の計算前のフローについてです。ここにYOLOXのキーアイディアの多くが集結されています。
数値設定
入力画像の解像度は512×512とします。Ground TruthのBounding Boxを、$(c_x, c_y, w, h)$というフォーマットで表します(ここで$c_x, c_y$はBounding Boxの中心点、$w, h$はBounding Boxの幅・高さを表します)。今1枚の画像に以下の3つのBounding Boxがあったとします。
- (100, 100, 50, 200)
- (200, 300, 200, 100)
- (300, 100, 100, 50)
コードで見ていくのは、公式実装のYOLOHead内のget_in_boxes_infoという関数です。YOLOXのコードを数時間追っていましたが、Headのこの部分の挙動がわかると、特に理解が進みそうだなと思いました。
この関数は以下のパラメーターがあります。引数にコメントを書いてみました。特徴マップ(グリッド)内にBounding Boxの中心があることや、Bounding Boxを含むことのフラグを求めたいのです。フラグから直接ロスは計算できませんが、後述のSimOTAというモジュールで役立ちます。
def get_in_boxes_info(
self,
gt_bboxes_per_image, # Ground TruthのBounding Boxの座標[num_gt, 4]
expanded_strides, # 特徴マップにおけるダウンサンプリング倍率, 数値
x_shifts, # アンカーのxインデックス [total_num_anchors]
y_shifts, # アンカーのyインデックス [total_num_anchors]
total_num_anchors, # アンカー数(アンカーフリーなので、=特徴マップの縦×横), 数値
num_gt, # 1枚の画像におけるBounding Boxの数, 数値
):
# 中略
# is_in_boxes_anchor: アンカーの中心がBounding Boxに含まれるか、またはMulti Positivesのエリア内にいるか [total_num_anchors]
# is_in_boxes_and_center: Bounding Box単位でPositiveなアンカーのみ抽出した行列 [num_gt, num_valid_anchors] (num_valid_anchors < total_num_anchors)
return is_in_boxes_anchor, is_in_boxes_and_center
数値例ではこれらの引数を決定的に与えます。
import torch
import torchvision
import matplotlib.pyplot as plt
# GTのBounding Box [中央のx, 中央のy, w, h]とする
gt_bboxes_per_image = torch.FloatTensor([
[100, 100, 50, 200],
[200, 300, 200, 100],
[300, 100, 100, 50]])
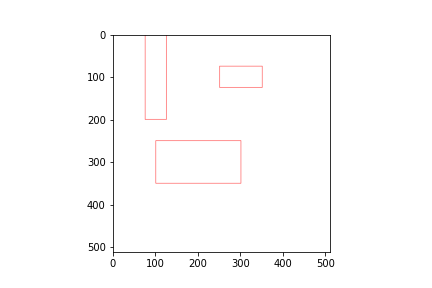
Bouding Boxをプロットしてみましょう(これは直接はYOLOXには関係ありません)。
dummy_img = torch.full((3, 512, 512), 255, dtype=torch.uint8)
gt_bboxes_per_image_topleft_wh = torch.cat([gt_bboxes_per_image[:,:2]-gt_bboxes_per_image[:,2:]/2,
gt_bboxes_per_image[:,:2]+gt_bboxes_per_image[:,2:]/2], dim=-1)
dummy_img = torchvision.utils.draw_bounding_boxes(dummy_img, gt_bboxes_per_image_topleft_wh, colors="red")
plt.imshow(dummy_img.permute(1, 2, 0)) # CHW -> HWC
簡略化した例なので、引数も決定的に与えます。
expanded_strides_per_image=torch.Tensor([32])
num_gt = gt_bboxes_per_image.shape[0] # 3
各ピクセルの中心点を求める
次は各アンカー(特徴マップの1ドット)の中心点が、元の画像で(元のスケールで)どの座標に対応するのかを求めます。y, xを総当りにしたグリッドが必要です。実際は他の関数で作っているのですが、簡略化のために今ここで作ります。
yv, xv = torch.meshgrid([torch.arange(16), torch.arange(16)]) # 512 / 32 = 16
grid = torch.stack([xv, yv], dim=-1).view(-1, 2) # [16, 16, 2] -> [256, 2]
x_shifts = grid[:,0].unsqueeze(0) # [1, 256]
y_shifts = grid[:,1].unsqueeze(0) # [1, 256]
後で「num_gt, total_num_anchors」というshapeにしたいので、x_shifts, y_shiftsの最初に軸を追加します。ここでx_shifts[0], y_shifts[0]を表示すると、
tensor([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1,
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3,
(中略)
10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
12, 13, 14, 15])
tensor([ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2,
(中略)
14, 14, 14, 14, 14, 14, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15, 15,
15, 15, 15, 15])
というふうに総当りでx, yのインデックスが出力されているのがわかります。x_shifts, y_shiftsの要素数が```total_num_anchors``になります。アンカーとは言っているものの、1ドットにつき1アンカーで、アンカーフリーのモデルです。各点の元のスケールでの座標は、
x_shifts_per_image = x_shifts[0] * expanded_strides_per_image
y_shifts_per_image = y_shifts[0] * expanded_strides_per_image
x_centers_per_image = (
(x_shifts_per_image + 0.5 * expanded_strides_per_image)
.unsqueeze(0)
.repeat(num_gt, 1)
) # [n_anchors] -> [num_gt, total_num_anchors]
y_centers_per_image = (
(y_shifts_per_image + 0.5 * expanded_strides_per_image)
.unsqueeze(0)
.repeat(num_gt, 1)
)
あとの計算の都合上、num_gt回コピーしておきます。同様にx_centers_per_image[0], y_centers_per_image[0]を表示すると(最初のインデックスはコピーされているので勝手に0とおいてOKです)、
tensor([ 16., 48., 80., 112., 144., 176., 208., 240., 272., 304., 336., 368.,
400., 432., 464., 496., 16., 48., 80., 112., 144., 176., 208., 240.,
(中略)
16., 48., 80., 112., 144., 176., 208., 240., 272., 304., 336., 368.,
400., 432., 464., 496.])
tensor([ 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16., 16.,
16., 16., 16., 16., 48., 48., 48., 48., 48., 48., 48., 48.,
(中略)
496., 496., 496., 496., 496., 496., 496., 496., 496., 496., 496., 496.,
496., 496., 496., 496.])
先程のインデックスが32倍されて+16されているのがわかります。これは元のスケールでのアンカーの座標です。アンカーの数も定数としておいておきましょう。
total_num_anchors = x_centers_per_image.shape[1] # 256
16×16の特徴マップなので、アンカーの数は256です。
Bounding Boxの上下左右の点
次にGTのBounding Boxの上下左右の座標を求めます。これは各アンカー(特徴マップの1ピクセル)内に中心があるかどうかを計算するために使います。
gt_bboxes_per_image_l = (
(gt_bboxes_per_image[:, 0] - 0.5 * gt_bboxes_per_image[:, 2])
.unsqueeze(1)
.repeat(1, total_num_anchors)
)
gt_bboxes_per_image_r = (
(gt_bboxes_per_image[:, 0] + 0.5 * gt_bboxes_per_image[:, 2])
.unsqueeze(1)
.repeat(1, total_num_anchors)
)
gt_bboxes_per_image_t = (
(gt_bboxes_per_image[:, 1] - 0.5 * gt_bboxes_per_image[:, 3])
.unsqueeze(1)
.repeat(1, total_num_anchors)
)
gt_bboxes_per_image_b = (
(gt_bboxes_per_image[:, 1] + 0.5 * gt_bboxes_per_image[:, 3])
.unsqueeze(1)
.repeat(1, total_num_anchors)
)
単なる「(中心x, 中心y, 幅, 高さ)→(左上x, 右下x, 左上y, 右下y)」への変換です。各変数は2つ目の軸について、total_num_anchors回コピーしたものなので、最初のスライスのみ表示します。
print(gt_bboxes_per_image_l[:,0]) # Bounding Boxの左x
print(gt_bboxes_per_image_r[:,0]) # Bounding Boxの右x
print(gt_bboxes_per_image_t[:,0]) # Bounding Boxの上y
print(gt_bboxes_per_image_b[:,0]) # Bounding Boxの下y
# tensor([ 75., 100., 250.])
# tensor([125., 300., 350.])
# tensor([ 0., 250., 75.])
# tensor([200., 350., 125.])
最初に定義したgt_bboxes_per_imageと比較してみましょう。1つ目のBounding Boxは中心が(100, 100)、幅が50なので、左xは75、右yは125となります。高さは200なので、上yは0、下yは200となります。これらはgt_bboxes_per_image_l[0,0], ..., gt_bboxes_per_image_b[0,0]に等しいです。gt_bboxes_per_image_l[:,0]などのスライスは各Bounding Boxのインデックスに対応し、同様に計算すると2つ目3つ目のBounding Boxも等しいことがわかります。
# (再掲)GTのBounding Box [中央のx, 中央のy, w, h]とする
gt_bboxes_per_image = torch.FloatTensor([
[100, 100, 50, 200],
[200, 300, 200, 100],
[300, 100, 100, 50]])
アンカーの中心がBounding Boxの内側にあるか
各アンカーの中心がBounding Boxの内側にあるかどうかを調べるために、各アンカーの中心座標(元の画像スケールでの座標)からBounding Boxの4隅までの座標差を求めます。アンカーの中心がBounding Box内にあるということと、4隅までの座標の差が全て0以上というのは同じことです。
b_l = x_centers_per_image - gt_bboxes_per_image_l # [num_gt, 1] - [1, total_num_anchors]
b_r = gt_bboxes_per_image_r - x_centers_per_image
b_t = y_centers_per_image - gt_bboxes_per_image_t
b_b = gt_bboxes_per_image_b - y_centers_per_image
bbox_deltas = torch.stack([b_l, b_t, b_r, b_b], 2) # [num_gt, total_num_anchors, 4]
各計算は(num_gt, 1)というshapeの行列と、(1, total_num_anchors)というshapeの行列の差をとるもので、num_gt, total_num_anchorsへ自動的にブロードキャストしています。bbox_deltasを表示すると、
tensor([[[ -59., 16., 109., 184.],
[ -27., 16., 77., 184.],
[ 5., 16., 45., 184.],
...,
[ 357., 496., -307., -296.],
[ 389., 496., -339., -296.],
[ 421., 496., -371., -296.]],
[[ -84., -234., 284., 334.],
[ -52., -234., 252., 334.],
[ -20., -234., 220., 334.],
...,
[ 332., 246., -132., -146.],
[ 364., 246., -164., -146.],
[ 396., 246., -196., -146.]],
[[-234., -59., 334., 109.],
[-202., -59., 302., 109.],
[-170., -59., 270., 109.],
...,
[ 182., 421., -82., -371.],
[ 214., 421., -114., -371.],
[ 246., 421., -146., -371.]]])
shapeはこのケースでは(3, 256, 4)となります。最初の2行について見ると、アンカーのインデックスがx方向に1増えているので、bbox_deltas[:,1,0]はbbox_deltas[:,0,0]より常に32(expanded_strides)大きいことがわかります。
アンカー内Bounding Boxがあるかどうか調べましょう。
is_in_boxes = bbox_deltas.min(dim=-1).values > 0.0 # [num_gt, total_num_anchors]
is_in_boxes_all = is_in_boxes.sum(dim=0) > 0 # [total_num_anchors]
print(is_in_boxes.shape) # torch.Size([3, 256])
print(is_in_boxes_all.shape) # torch.Size([256])
各Bounding Box、各アンカーに対し、アンカーの中心がBounding Boxの内側にあるかはbbox_deltasの最後の軸の周りの最小値が0より大きいかどうかを調べます(is_in_boxes)。is_in_boxes_allはBounding Boxの軸でまとめたもので、各アンカーに対し、いずれかのBounding Boxを含んでいるかどうかを求めたものです。
以下のコードは必要ないものですが、実際にどのアンカーが含まれているかを見ると、
print(torch.where(is_in_boxes))
print(torch.where(is_in_boxes_all))
(tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2]), tensor([ 2, 3, 18, 19, 34, 35, 50, 51, 66, 67, 82, 83, 131, 132,
133, 134, 135, 136, 147, 148, 149, 150, 151, 152, 163, 164, 165, 166,
167, 168, 40, 41, 42, 56, 57, 58]))
(tensor([ 2, 3, 18, 19, 34, 35, 40, 41, 42, 50, 51, 56, 57, 58,
66, 67, 82, 83, 131, 132, 133, 134, 135, 136, 147, 148, 149, 150,
151, 152, 163, 164, 165, 166, 167, 168]),)
ここでのアンカーのインデックスは縦横をならしたものです。Bounding Boxの大きさについて、1つ目は「50×200」、2つ目は「200×100」、3つ目は「100×50」でしたので、面積は2>1>3です。torch.where(is_in_boxes)の返り値の1つ目を見ると、面積の大きいBounding Boxがよくカウントされているのがわかります。is_in_boxes_allは単にORで集約したものです。
Multi Positives
YOLOXの工夫点の1つにMulti Positivesがあります。古典的な物体検出のモデルの場合、「GTのBounding Boxの中心があるアンカーのみPositiveとして評価する」というものでしたが、「その近傍3×3アンカーも一律にPositiveとして評価」するという改良を行っています。元ネタはFCOSで使われていたcenter samplingです。
Multi positivesの目的は、データ不均衡対策です。16×16=256個のアンカーがある例を想定します。もしBounding Boxの中心があるアンカーのみを評価する場合、Bouding Boxが3個あればPositive=3:Negative=253と著しい不均衡になります。Bouding Boxが1つのアンカーに収まることはほとんどなく、実際は複数のアンカーにまたがることが多いため、「えいやっ」で近傍3×3アンカーもPositiveとみなしてもほとんど敵対的なサンプルとならないと考えられます。仮にBounding Box同士の重なりがない場合、3×3アンカーをPositiveとみなせば「P:N=27:229」、5×5アンカーをPositiveとみなせば「P:N=75:178」と大きく不均衡改善できます。
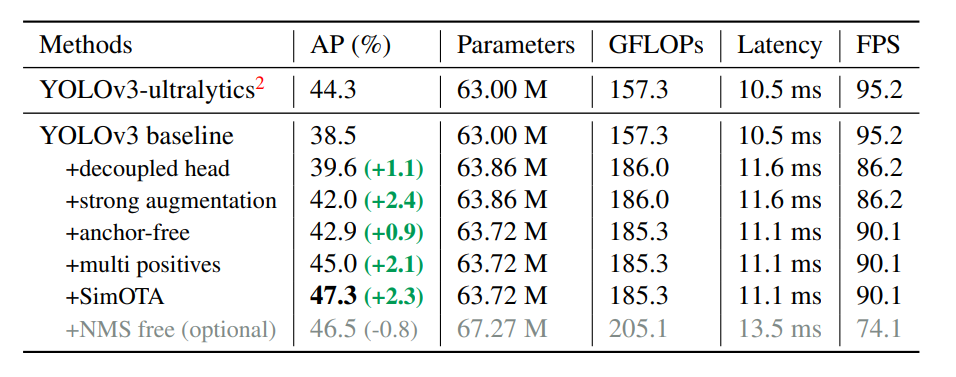
定量評価で見ると、Multi PositivesはかなりのAPの向上に寄与しており、APで2.1の向上、Strong Augmentationに匹敵します。
ここがややこしいかったのですが、論文では「中心の3×3のエリアをPositiveとする」とあったのに、実際のコードだと5×5のエリアをPositiveとしているようにしか見えないことです。もしかするとド真ん中を除いた上での近傍3×3エリアなのかもしれませんが、論文表記と実装でずれてることはたまにあるので、そういうものなんだなと思っておきます。ここでは公式コードの表記に準拠します。
Multi Positivesのエリアを計算する
近傍ピクセルの判定は、「Bounding Boxの中心を含むかどうか」の計算とほぼ同じです。
center_radius = 2.5 # 5x5エリアをPositive?
gt_bboxes_per_image_l = (gt_bboxes_per_image[:, 0]).unsqueeze(1).repeat(
1, total_num_anchors
) - center_radius * expanded_strides_per_image.unsqueeze(0)
gt_bboxes_per_image_r = (gt_bboxes_per_image[:, 0]).unsqueeze(1).repeat(
1, total_num_anchors
) + center_radius * expanded_strides_per_image.unsqueeze(0)
gt_bboxes_per_image_t = (gt_bboxes_per_image[:, 1]).unsqueeze(1).repeat(
1, total_num_anchors
) - center_radius * expanded_strides_per_image.unsqueeze(0)
gt_bboxes_per_image_b = (gt_bboxes_per_image[:, 1]).unsqueeze(1).repeat(
1, total_num_anchors
) + center_radius * expanded_strides_per_image.unsqueeze(0)
c_l = x_centers_per_image - gt_bboxes_per_image_l
c_r = gt_bboxes_per_image_r - x_centers_per_image
c_t = y_centers_per_image - gt_bboxes_per_image_t
c_b = gt_bboxes_per_image_b - y_centers_per_image
center_deltas = torch.stack([c_l, c_t, c_r, c_b], 2)
is_in_centers = center_deltas.min(dim=-1).values > 0.0
is_in_centers_all = is_in_centers.sum(dim=0) > 0
先程と異なるのは、gt_bboxes_per_image_lなどが自身の中央の座標を基準として引いているのではなく、expanded_strides_per_imageという特徴マップ→元画像への倍率という固定値で決められることです。例えば、gt_bboxes_per_image_lを見てみると(printが長過ぎるのでgt_bboxes_per_image_l[:, :5]とスライスしています)
// print(gt_bboxes_per_image_l[:, :5])
tensor([[ 20., 20., 20., 20., 20.],
[120., 120., 120., 120., 120.],
[220., 220., 220., 220., 220.]])
と一定値であることがわかります。is_in_centersはPositiveであるかのフラグを示し、先程と同様にprintすると、
print(torch.where(is_in_centers))
print(torch.where(is_in_centers_all))
(tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2]), tensor([ 17, 18, 19, 20, 21, 33, 34, 35, 36, 37, 49, 50, 51, 52,
53, 65, 66, 67, 68, 69, 81, 82, 83, 84, 85, 116, 117, 118,
119, 120, 132, 133, 134, 135, 136, 148, 149, 150, 151, 152, 164, 165,
166, 167, 168, 180, 181, 182, 183, 184, 23, 24, 25, 26, 27, 39,
40, 41, 42, 43, 55, 56, 57, 58, 59, 71, 72, 73, 74, 75,
87, 88, 89, 90, 91]))
(tensor([ 17, 18, 19, 20, 21, 23, 24, 25, 26, 27, 33, 34, 35, 36,
37, 39, 40, 41, 42, 43, 49, 50, 51, 52, 53, 55, 56, 57,
58, 59, 65, 66, 67, 68, 69, 71, 72, 73, 74, 75, 81, 82,
83, 84, 85, 87, 88, 89, 90, 91, 116, 117, 118, 119, 120, 132,
133, 134, 135, 136, 148, 149, 150, 151, 152, 164, 165, 166, 167, 168,
180, 181, 182, 183, 184]),)
先程のis_in_boxesやis_in_boxes_allと異なり、Bounding Boxの大きさによらず常に一定のエリアがPositiveとなるように計算されています。
Positiveのエリアをマスクする
今までずっとYOLOHeadの実装内のget_in_boxes_infoという関数を見てきました。最終的に返り値としたいのはこの2つの変数です。
is_in_boxes_anchor = is_in_boxes_all | is_in_centers_all
is_in_boxes_and_center = (
is_in_boxes[:, is_in_boxes_anchor] & is_in_centers[:, is_in_boxes_anchor]
)
それぞれのshapeは、
print(is_in_boxes_anchor.shape) # torch.Size([256])
print(is_in_boxes_and_center.shape) # torch.Size([3, 80])
です。is_in_boxes_and_centerは「Bounding Boxの数, Positiveな有効アンカー数」を表します。「Bounding Boxを含んだアンカーか、中心がMulti Positivesのエリアにいるか」でフィルタリングしたものを返しています。実際にis_in_boxes_and_centerをtorch.whereで見ると、
(tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 2, 2, 2, 2, 2, 2]), tensor([ 3, 4, 13, 14, 23, 24, 33, 34, 43, 44, 58, 59, 60, 61, 62, 64, 65, 66,
67, 68, 70, 71, 72, 73, 74, 18, 19, 20, 28, 29, 30]))
ある程度Bounding Boxの大きさに影響しているものの、Multi Positivesの影響で、Bounding Boxの大きさによらずに一定数のアンカー数は保証できています。
Positiveなアンカーのマスクとして使う
今まで頑張って求めたis_in_boxes_anchorは、ロス計算をする際の有効なアンカーをマスクするときに使いたいのです。これから見るのはコードのget_assignmentsという関数内です。
今、バックボーンのネットワークが、$H, W$という解像度の特徴マップを出したとしましょう。これはもともとの解像度$H_{orig}, W_{orig}$がネットワーク内でダウンサンプリングされたものです。先程の数値例では、$H_{orig}=W_{orig}=512, H=W=16$でしたね。
図の下の「YOLOX Decoupled Head」というHeadを通ります。「Decoupled Head」と書いていますが、Headのレイヤーを複数にしたりBranchさせたり、全てネットワーク層レベルで説明できる話です。
「分類、回帰、IoU」のそれぞれの予測をします。それぞれのチャンネル数の意味は、分類はクラス数$C$、回帰はBounding Boxの4パラメーターです。ただこれをそのままロス計算には使えなく、Positiveであるアンカーのマスクが必要になります。なぜなら、物体がないエリアでは、分類や回帰が意味のない値を出すため、そのままロス計算に使うとノイズになるからです。
そこで必要になるのが今まで求めたis_in_boxes_anchorという変数です。これはPositiveなアンカーをマスクする「Foreground mask」になります。実際のコードのget_assignmentsを見ると、(この関数はロス計算で呼び出されるものです)
fg_mask, is_in_boxes_and_center = self.get_in_boxes_info(
gt_bboxes_per_image,
expanded_strides,
x_shifts,
y_shifts,
total_num_anchors,
num_gt,
) # fg_mask = is_in_boxes_anchor [A_pos,]
bboxes_preds_per_image = bboxes_preds_per_image[fg_mask] # [A, 4] -> [A_pos, 4]
cls_preds_ = cls_preds[batch_idx][fg_mask] # [N, A, C] -> [A_pos, C]
obj_preds_ = obj_preds[batch_idx][fg_mask] # [N, A, 1] -> [A_pos, 1]
num_in_boxes_anchor = bboxes_preds_per_image.shape[0]
全体のアンカーの個数を$A$とすると、アンカー数は特徴マップの解像度縦×横に相当するので$A=HW$となります。これを$A_{pos}<A$なる有効なアンカー数$A_{pos}$までマスクします。$A$は固定値ですが、$A_{pos}$は画像や訓練タイミングによって異なるので変動値です。
SimOTA
ただ、ここで出てきたBounding Boxの予測値は、Ground Truthよりもさらに多くのBoxを含んでいるために、ロス計算時に程度絞り込まないといけません。最も単純な方法は、GTとのIoUが最も高いBoxについて評価すればいいです。ただ、Boxが重なり合っている場合は、1つの予測Boxに対し複数のGTのBoxを割り当ててしまうため、曖昧なアンカーになってしまいます。
これについての解決策の1つがOTA(Optimal Transport Assignment)と呼ばれるアルゴリズムです。YOLOXもOTAをベースとしています。OTAの論文からの引用です。
OTAではGT1やGT2のように、GTが重なり合ったBoxについて焦点を当てています。重なりあうとロス計算でどちらのBounding Boxで計算していいかわからず、「曖昧なアンカー(Ambiguous Anchor)」となってしまうためです。このOTAの論文、著者が早稲田大学とメグビーの方で、著者の一部に日本人がいます。ここではOTAの詳細な解説は行いません。以下に解説記事があるので参照してください。
- 【論文5分まとめ】Ota: Optimal transport assignment for object detection
- 【CVPR2021】物体検出のラベルアサインメントを最適化するOTAを紹介!
OTAではこれを最適輸送問題として捉え、Sinkhorn-Knoppアルゴリズムを用いて解決していました。ただ、このSinkhorn-Knoppアルゴリズムの計算量が重く、訓練時間が25%増えてしまいます。そこで、OTAを計算量の少ない形で簡易的に模擬したものが、YOLOXにおけるSimOTAです。SimOTAとはOTAをSimulationをしているからSimOTAなのです。
具体的にはtop_kの関数を多用します。コードではHead内のdynamic_k_matchingという関数がそれです。これも簡単な数値例で見ていきましょう。
数値例の設定
元画像の解像度は512、特徴マップの解像度は16×16とし、GTのBounding Boxは先程と同じ値を使います。これに対し、予測のBounding Boxが9個出てきたとします。
import torch
import torchvision
import matplotlib.pyplot as plt
# GTのBounding Box [中央のx, 中央のy, w, h]とする
gt_bboxes_per_image = torch.FloatTensor([
[100, 100, 50, 200],
[200, 300, 200, 100],
[300, 100, 100, 50]])
pred_bboxes_per_image = torch.FloatTensor([
[80, 90, 55, 190],
[90, 110, 50, 205],
[110, 105, 45, 195],
[195, 260, 190, 105],
[210, 290, 205, 95],
[235, 310, 195, 110],
[330, 80, 110, 60],
[280, 125, 105, 45],
[350, 100, 90, 55]])
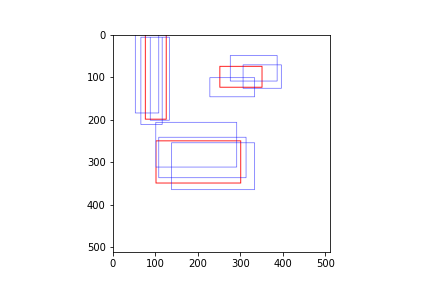
フォーマットは先ほどと同様「中央のx, 中央のy, w, h」です。GTを赤、予測を青でプロットしてみます。
def centerwh_to_xyxy(center_wh):
return torch.cat([
center_wh[:, :2] - center_wh[:, 2:] / 2,
center_wh[:, :2] + center_wh[:, 2:] / 2,
], dim=-1)
dummy_img = torch.full((3, 512, 512), 255, dtype=torch.uint8)
dummy_img = torchvision.utils.draw_bounding_boxes(dummy_img,
centerwh_to_xyxy(gt_bboxes_per_image), colors="red", width=2)
dummy_img = torchvision.utils.draw_bounding_boxes(dummy_img,
centerwh_to_xyxy(pred_bboxes_per_image), colors="blue", width=1)
plt.imshow(dummy_img.permute(1, 2, 0))
Pair-wiseのIOUの計算
各Bounding Boxに対し「GT×Pred」の総当りの形式でIoUを計算します。実装ではこちらにあたります。
def bboxes_iou(bboxes_a, bboxes_b, xyxy=True):
if bboxes_a.shape[1] != 4 or bboxes_b.shape[1] != 4:
raise IndexError
if xyxy:
tl = torch.max(bboxes_a[:, None, :2], bboxes_b[:, :2])
br = torch.min(bboxes_a[:, None, 2:], bboxes_b[:, 2:])
area_a = torch.prod(bboxes_a[:, 2:] - bboxes_a[:, :2], 1)
area_b = torch.prod(bboxes_b[:, 2:] - bboxes_b[:, :2], 1)
else:
tl = torch.max(
(bboxes_a[:, None, :2] - bboxes_a[:, None, 2:] / 2),
(bboxes_b[:, :2] - bboxes_b[:, 2:] / 2),
)
br = torch.min(
(bboxes_a[:, None, :2] + bboxes_a[:, None, 2:] / 2),
(bboxes_b[:, :2] + bboxes_b[:, 2:] / 2),
)
area_a = torch.prod(bboxes_a[:, 2:], 1)
area_b = torch.prod(bboxes_b[:, 2:], 1)
en = (tl < br).type(tl.type()).prod(dim=2)
area_i = torch.prod(br - tl, 2) * en # * ((tl < br).all())
return area_i / (area_a[:, None] + area_b - area_i)
出力は(num_gt, num_pred)の形式になります。このケースではGTが3個、Predが9個なので3×9行列になります。計算されたpair_wise_iousを表示してみましょう。
pair_wise_ious = bboxes_iou(gt_bboxes_per_image, pred_bboxes_per_image, xyxy=False) # [n_gt, A_pos]
tensor([[0.4165, 0.6135, 0.6247, -0.0000, -0.0000, 0.0000, -0.0000, -0.0000, -0.0000],
[-0.0000, -0.0000, -0.0000, 0.4230, 0.7443, 0.5935, -0.0000, -0.0000, 0.0000],
[-0.0000, -0.0000, -0.0000, -0.0000, -0.0000, -0.0000, 0.2925, 0.2359, 0.2922]])
このケースでは最も高いIoUの予測BoxにGTを割り当てれば良さそうなので、楽ですね。
SimOTAのためのコスト計算
次にSimOTAのためのコストを計算します。今見てるのはYOLOHeadのget_assignmentsの関数内の処理です。
最適輸送問題を解くために、予測→GTへの輸送コストを求めます。これは損失関数ベースでOKです。IoUの負の対数を取ってロスに変えます(クロスエントロピーと若干似ていて面白いですね)。
pair_wise_ious_loss = -torch.log(pair_wise_ious + 1e-8)
tensor([[ 0.8760, 0.4885, 0.4705, 18.4207, 18.4207, 18.4207, 18.4207, 18.4207,
18.4207],
[18.4207, 18.4207, 18.4207, 0.8604, 0.2954, 0.5218, 18.4207, 18.4207,
18.4207],
[18.4207, 18.4207, 18.4207, 18.4207, 18.4207, 18.4207, 1.2294, 1.4443,
1.2303]])
本来はクラス分類や、有効なアンカーかどうか(先程求めたis_in_boxes_and_centerかどうか)も考慮してコスト計算するのですが、今わかりやすくするためにこれらは全てあっていると仮定します。コストではIoUだけ考慮します。
# 分類は全てあっていると仮定する
pair_wise_cls_loss = torch.zeros_like(pair_wise_ious_loss)
# 全て有効なアンカー内にあると仮定する
is_in_boxes_and_center = torch.ones(pair_wise_ious_loss.shape, dtype=torch.bool)
cost = (
pair_wise_cls_loss
+ 3.0 * pair_wise_ious_loss
+ 100000.0 * (~is_in_boxes_and_center)
) # 問題を簡略化しIoUだけで考えるのでpair_wise_ioss_lossの3倍
tensor([[ 2.6280, 1.4655, 1.4116, 55.2620, 55.2620, 55.2620, 55.2620, 55.2620,
55.2620],
[55.2620, 55.2620, 55.2620, 2.5813, 0.8861, 1.5653, 55.2620, 55.2620,
55.2620],
[55.2620, 55.2620, 55.2620, 55.2620, 55.2620, 55.2620, 3.6881, 4.3330,
3.6909]])
今IoU以外は無視していますが、有効な範囲外にある(is_in_boxes_and_center=Falseのアンカー)には10万という高いペナルティーをかけていますね。幸いMulti Positivesも一緒に入れているので、割当先がなくなって困るということはなさそうです。あくまでこれはSimOTAにおける割当先計算のためのコストであって、損失関数の値とは異なります。
Dynamic K
今基本的にget_assignmentsの処理を見ているのですが、そこから呼び出されるdynamic_k関数の処理を見ます。ここがSimOTAの実装です。
関数名になっているDynamic Kとは何かというと、GTに対して割り当てる予測Bounding Boxの数を動的に調整するということです。最低1個は割り当てますが、予測のBounding Boxが多ければもっと多く割り当てるようにします。
num_gt = gt_bboxes_per_image.shape[0]
matching_matrix = torch.zeros_like(cost, dtype=torch.uint8)
ious_in_boxes_matrix = pair_wise_ious # [num_gt, num_pred]
n_candidate_k = min(10, ious_in_boxes_matrix.size(1))
topk_ious, _ = torch.topk(ious_in_boxes_matrix, n_candidate_k, dim=1)
dynamic_ks = torch.clamp(topk_ious.sum(1).int(), min=1)
dynamic_ks = dynamic_ks.tolist()
この処理は何をやっているかというと、Pair-wise IOUに対し、Predについての上位10個のIoUの和を求め、それを切り捨てた値をn_candidate_kとする単純ながら大胆な方法です。
今回の例では、n_candidate_k=9なので、予測Bounding Box全てを使います。topk_iousは各GTに対してIoUで降順ソートして上位10件を求めたものです。
// print(topk_ious)
tensor([[0.6247, 0.6135, 0.4165, -0.0000, -0.0000, -0.0000, 0.0000, -0.0000, -0.0000],
[0.7443, 0.5935, 0.4230, 0.0000, -0.0000, -0.0000, -0.0000, -0.0000, -0.0000],
[0.2925, 0.2922, 0.2359, -0.0000, -0.0000, -0.0000, -0.0000, -0.0000, -0.0000]])
予測のBoxが100件も200件もあれば、このTake(10)のプロセスが意味をなしてきます。dynamic_ksはGTに対する割当の個数を表しますが、topk_ious.sum(1).int()をベースに求めています。切り捨て前の値を見てみると、
print(topk_ious.sum(1)) # tensor([1.6547, 1.7607, 0.8206])
数値例では、あまりに単純すぎたのかGTに対して1個ずつ割り当てるという、面白みに欠ける結果となりました。
とりあえずコストの低い順に割り当てる
ここでインチキをして、dynamic_ksの計算前にIoUに対して0.5を足すということをします。これにより複数の予測を割り当てることをシミュレートできます。
dynamic_ks = torch.clamp((topk_ious.sum(1) + 0.5).int(), min=1) # これはインチキなので本番ではやらなくていい
dynamic_ks = dynamic_ks.tolist()
print(dynamic_ks) # [2, 2, 1]
1, 2番目のGTに対しては、2個ずつ予測を割り当てるように強引に改変しました。割り当ては次のコードです(このブロックは公式コードの通りで、インチキしていません)。
for gt_idx in range(num_gt):
_, pos_idx = torch.topk(
cost[gt_idx], k=dynamic_ks[gt_idx], largest=False
)
matching_matrix[gt_idx][pos_idx] = 1
できあがったmatching_matrixを見てみましょう。
tensor([[0, 1, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 0]], dtype=torch.uint8)
行がGTで、列が予測です。予測の2,3番目はGTの1番目に、予測の5,6番目はGTの2番目に、予測の7番目はGTの3番目に割り当てられているのがわかります。インチキをしましたが、複数のGTに対して割り当てられている「曖昧なアンカー」がありませんね。これではSimOTAっぽくないです。
複数に割り当てられているアンカーをどうするのか
さらにインチキをします。予測の3番目がGTの2番目に割り当てられるように細工をします。
matching_matrix[1, 2] = 1 # 重複を作るインチキ。当然ながら本番でやってはいけない
print(matching_matrix)
# tensor([[0, 1, 1, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 0, 1, 1, 0, 0, 0],
# [0, 0, 0, 0, 0, 0, 1, 0, 0]], dtype=torch.uint8)
これで予測の3番目が曖昧なアンカーになりました。曖昧なアンカーとはmatching_matrixが複数の行に割り当てられている列とみなすこともできます。このコードは公式のままです。
anchor_matching_gt = matching_matrix.sum(0)
if (anchor_matching_gt > 1).sum() > 0: # 1つのBoxに複数割り当てられた場合
_, cost_argmin = torch.min(cost[:, anchor_matching_gt > 1], dim=0)
matching_matrix[:, anchor_matching_gt > 1] *= 0
matching_matrix[cost_argmin, anchor_matching_gt > 1] = 1
ここで行っているのは「曖昧なアンカーに対し、コストが低くなるように再選択」です。再選択されたmatching_matrixを見ると、
tensor([[0, 1, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 0]], dtype=torch.uint8)
先程インチキした[1,2]の割り当てが解除されていますね。インチキで入れた割り当てはIoUが低い(コストが高い)ので解除されるのは当たり前でしょう。
fg_mask_inboxes = matching_matrix.sum(0) > 0
matched_gt_inds = matching_matrix[:, fg_mask_inboxes].argmax(0)
pred_ious_this_matching = (matching_matrix * pair_wise_ious).sum(0)[
fg_mask_inboxes
]
print(fg_mask_inboxes)
# tensor([False, True, True, False, True, True, True, False, False])
print(matched_gt_inds)
# tensor([0, 0, 1, 1, 2])
print(pred_ious_this_matching)
# tensor([0.6135, 0.6247, 0.7443, 0.5935, 0.2925])
あとはそうですねという感じの出力です。
結局なにをやったのか
今までコード単位で細かくみたので全体図がわかりづらいですが、訓練時のロス計算のフローはこういうことです。YOLOHeadのDecoupled Headの出力は、画像1枚あたり
$$(H, W, \cdot)$$
というshapeでした。最終チャンネルはクラス予想($C$)か、BoundingBoxの回帰か(4)、IoUか(1)で異なります。これを有効なアンカーのみ抽出し(Multi Positives)など、
$$(A_{pos}, \cdot)\quad A_{pos}<A=HW$$
というshapeに変形します。ただこれだと予測のBoxとGTのBoxのリンクが取れないので、Dynamic kを用い、
B_{gt}^{i} \to \{B_{pred, 1}^{i}, \cdots, B_{pred, j}^{i}, \cdots, B_{pred, K^i}^{i}\}
というマッピングを作ります。ここで$i\in[1, n_{gt}]$で、$n_{gt}$はGTのBounding Boxの数です。$B_{gt}^i$は$i$番目のGTのBounding Box、$B_{pred, j}, j\in[1, K^i]$は予測のBounding Boxです。$K^i$がDynamic Kで求められた、$i$番目のGTに対する紐付ける予測のBounding Boxの数。ここでDynamic Kの数の和
$$A_{SimOTA} = \sum_{i=1}^{n_{gt}} K^i$$
として、クラス、Bounding Box、IoUの予想を、
$$(A_{SimOTA}, \cdot), \qquad A_{SimOTA} \leq A_{pos} < A$$
にマッピングします。Dynamic Kで常に1つの予測Bounding Boxしか紐付けない($K^i=1$)なら、$A_{SimOTA}=n_{gt}$となります。あとは単純にロスを計算するだけです。
推論時はどうするの?
今のは訓練時の話で、推論時はGTのラベルによる紐付けができません。アンカーの数をどう減らしているのかと思っていたのですが、実は単純でした。
答:出力のアンカーを何もしない。NMSに任せるだけ
これまで見てきたのは訓練時のロス計算の話で、YOLOHeadのforward内では、
# YOLOHeadのforward内
if self.training:
return self.get_losses(
imgs,
x_shifts,
y_shifts,
expanded_strides,
labels,
torch.cat(outputs, 1),
origin_preds,
dtype=xin[0].dtype,
)
という部分から全て呼び出されていました。つまり、推論時は今まで紹介してきた処理は何もしません。おわり。
後処理ってなにやってるの?
→座標系戻してNMSするだけ
具体的にはこちらのコード
NMSの重要性
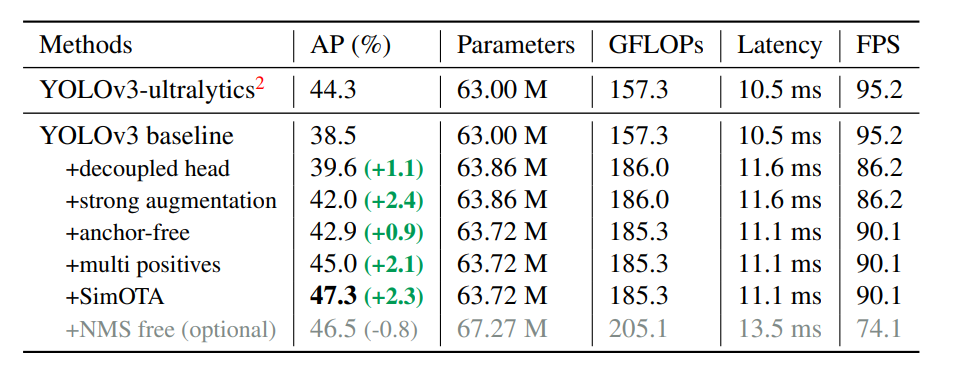
NMSフリーのモデルも出てきていますが、YOLOXではNMSフリー化するとスループットも悪くなり、APも0.8%下がりました。
ちなみにSimOTAは2.3%もAPの上昇に寄与しているので、いかに曖昧なアンカーが敵対的な役割を果たしてきたかがわかります。
ちなみにStrong Augmentationは?
MixUpとMosaic
「Mosaicってなんだろう?」と調べてみたらYOLOv4の論文に書かれていました。
4枚の画像を混ぜるだけ。簡単。発想的にはCutMixに近いですね。
他には「Color Jitter(HSVでノイズ入れる)」と「Horizontal Flip」だけです。YOLOv3にあったRandom CropはMosaicと重複するため削除したそうです。
まとめと感想
「YOLOX」では、アンカーフリー、Multi Positives、SimOTAという様々な訓練時の工夫を通じ、End-to-Endでシンプルな形ながら強力な精度を出すことに成功しています。
以前この論文見た時「自分物体検出の論文読んでなさすぎだよな。さすがに何か読まないとまずいよな」と思って、以前から宿題だった感があった論文でした。コードの細部を追うことでようやく全貌や工夫が見えました。全体的にシンプルで(アンカーフリーにしたのが良いと思います)、コードも読みやすく、居酒屋の「とりあえずビール」的な感覚で、「とりあえず初手YOLOX」はありなんじゃないかと思います。YOLOXがいいかYOLOv5がいいか、自分はYOLOv5を調べたことない(論文がないらしい?)ので大きなこと言えないですが、YOLOv1ぐらいのシンプルさを求めているのだったら、YOLOX使うのありだなと思いました。ぜひサンプルプログラム動かして体験してみたいモデルだなと思いました。
これで「2021年のディープラーニング論文を1人で読むAdvent Calendar」、無事完走です! 感想はまた追って書きますが、ここまでおつきあいいただきありがとうございました!
告知
このアドベントカレンダーが本になりました!
https://koshian2.booth.pm/items/3595424
Amazonでも扱いあります詳しくは👉 https://shikoan.com