GANの訓練がうまくいかないときにHingeロスを使うといいよという話

SPADE(GauGAN)の実装にインスパイアされて、GANにおけるHingeロスの有効性を確かめました。Dの損失が0に近くなるケースで、Hingeロスは生成画質の向上に寄与することを、理論的にも実験的にも示すことができました。

GANは必ずしもうまくいかない

論文で目にするGANというと、Big GANやStyle GANのように非常に高画質な画像が生成され、本物か偽物かわからない、「写真が証拠となる時代は終わった」とさえ言われることもあります。しかし、論文に見られるほんの上澄みの成功例を考えるのと、われわれが一から訓練してそのような高画質なモデルを作るのには大きな隔たりがあります。GANの訓練は画像分類や物体検出のような教師あり学習とは異なり、もっと泥臭いプロセスがあります。

GANでうまくいく例、失敗する例

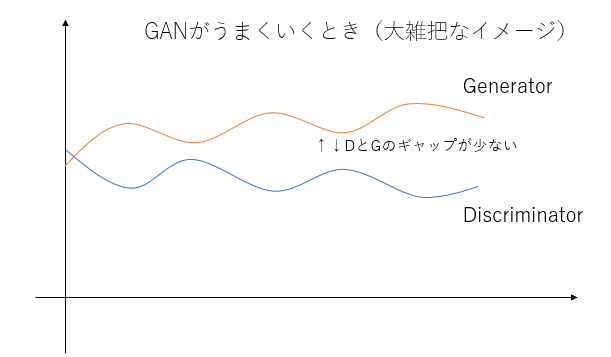
GANが泥臭い大きな理由は必ずしもうまくいかないこと、その観測例の大半にD（Discriminator）とG（Generator）の損失のギャップがあることです。画像分類や物体検出では、固定値のy_trueから損失を計算し勾配を得ます。一方でGANのGの勾配を計算では、変動値であるDを用います。GANはDを騙すように訓練することでGの訓練が進むため、DやGの一方（特にD）が強すぎると、Gの訓練が止まってしまいます。DとGの損失ギャップが少ないほど訓練が進みやすいのです。

このようなケースは学習が上手く進みます。一方が強くなりすぎないからです。

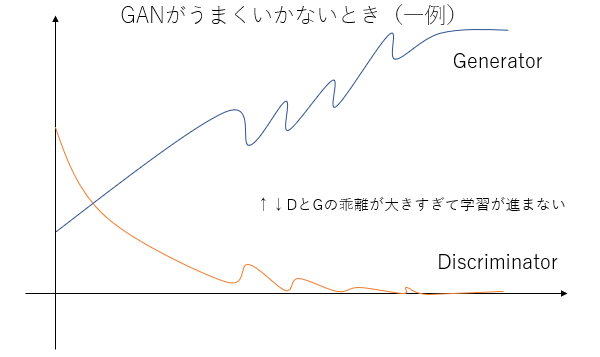
一方でうまくいかない例です。GよりDが強くなってしまうありがちなケースで、途中からGの学習が進みません。Dが強すぎて騙せないからです。この逆のケース（DではなくGが強くなりすぎる）ケースもありえますが、Dが強くなりすぎるケースのほうが遭遇しやすいです¹。そのため、今回はDが強くなりすぎるときの対策法について考えます。

いま、Dが強すぎるときにGの学習が進まないのを問題としているので、~~これはG側の勾配消失問題と考えることもできます。~~Dのロス=0が、GANの勾配消失問題とは違うよという指摘があったらぜひお願いします（丁寧にコメントしてくださった方がいるので、コメント欄を参照してください）。

交差エントロピーを紐解く

Dが強くなりすぎる原因について考えるには、画像分類のほか、DCGANのDに使われる損失関数「交差エントロピー」について振り返ったほうが良さそうです。$p$を本物か偽物かどうかの確率(0, 1)、$\tilde{p}$を予測確率とします。交差エントロピーの定義は、

$$-p\log(\tilde{p})-(1-p)\log(1-\tilde{p}) \tag{1}$$

です。次にロジットを考えます。ロジットとはシグモイド関数をかける前の値で、

$$x=\log\frac{p}{1-p} \tag{2}$$

という確率の対数オッズ比で与えられます。この式をpについて解くと、シグモイド関数の式$\frac{1}{1+e^{-x}}$が導出されるのでぜひ解いてみてください。

ロジットの値域は$[-\infty, \infty]$であるのに対して、確率の値域は$[0, 1]$です。つまりシグモイド関数のやっているのは、確率の定義にそぐうように実数全体から変換しているということです。

交差エントロピーの微分

実際の勾配計算は損失関数の微分で行いますから、交差エントロピーの微分を考えることが重要になります。$p=0,1$で固定すると、$\tilde{p}$だけの式に表せます。

$$\begin{cases}E_{p=0}=-\log(1-\tilde{p}) \\ E_{p=1}=-\log{\tilde{p}}\end{cases} \tag{3}$$

これを$\tilde{p}$で微分します。

\begin{cases}\frac{d}{d\tilde{p}}E_{p=0}=\frac{1}{1-\tilde{p}} \\  \frac{d}{d\tilde{p}}E_{p=1}=-\frac{1}{\tilde{p}}\end{cases} \tag{4}

これをロジット$x$の微分に直します。Chain ruleにより、

$$\frac{dE}{dx} =\frac{dE}{d\tilde{p}}\frac{d\tilde{p}}{dx} \tag{5}$$

ロジットとシグモイド関数の関係から、

$$\tilde{p}=\frac{1}{1+e^{-x}}=\sigma(x) \tag{6} $$

と表せます。シグモイド関数を$\sigma(x)$と表すことにします。また、シグモイド関数の微分は、この記事を参照すると

$$\frac{d}{dx}\sigma(x) =\frac{d\tilde{p}}{dx} = (1-\sigma(x))\sigma(x) \tag{7}$$

(4)～(7)より、$p=0,1$で固定したときの、交差エントロピーのロジットでの微分は、

\begin{cases}\frac{d}{dx}E_{p=0}=\frac{(1-\sigma(x))\sigma(x)}{1-\sigma(x)}=\sigma(x) \\  \frac{d}{dx}E_{p=1}=-\frac{(1-\sigma(x))\sigma(x)}{\sigma(x)}=\sigma(x)-1 \end{cases} \tag{8}

美しい結果となりました。交差エントロピーのロジットの微分はシグモイド関数ということがわかりました。

微分がシグモイド関数ということ

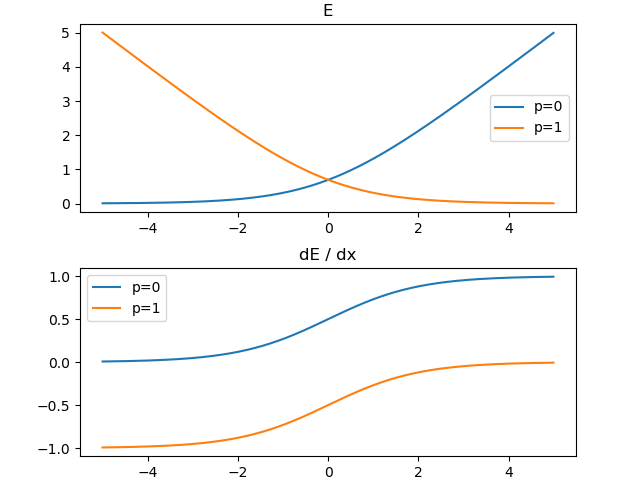
$p=0,1$で固定したときの、交差エントロピー$E$（縦軸）とロジット$x$（横軸）の関係をプロットしてみました。下段はその微分です。　

微分がシグモイド関数であることから、p=0の場合はxをマイナス方向にどんどん大きくしても、p=1の場合はxをプラス方向にどんどん大きくしても、Eの微分は0になることはありません。限りなく0に近くなるだけです。

p=0, 1はDにおいて本物/偽物の確率であったことを思い出すと、ずっと訓練している限り、Dにおける本物/偽物の乖離はずっと続いていくことになります。なぜならEの微分は0にならないからです。これがDが強くなりすぎる原因ではないでしょうか？

Hingeロス

SPADE(GauGAN)の公式実装を見ていたら面白いロスを使っていました。こちらのHingeロスの定義は次のとおりです。

\begin{cases}\
-\min(x-1, 0) & \text{if D and real} \\
-\min(-x-1, 0) & \text{if D and fake} \\
-x & \text{if G}
 \end{cases} \tag{9}

ここで$x$はロジットとします。Gの部分はただのロジットのマイナスですが、Dの部分がHinge関数ですね。Hingeロスはサポートベクターマシンの損失関数で使われます。

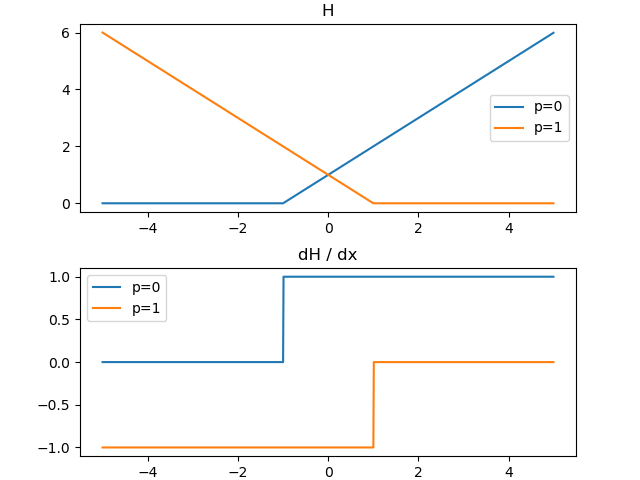
プロットしてみると次のようになります。

交差エントロピーとは異なり、Hingeロスは±1の範囲外では勾配が0になります。オフセットの入ったReLUと考えることもできます。

関連：LS-GAN

ロジットから直接損失関数を計算する試みは他にもあります。例えば、LS-GANはロジットに対して平均二乗誤差を計算します。DCGANに代表されるような通常のGANよりも高画質の出力が可能です。

$$\frac{1}{2}(x-z)^2 \qquad z=0 \text{ if D_fake else } z=1 \tag{10}$$

交差エントロピー、LS-GAN（平均二乗誤差）、Hingeロスの可視化

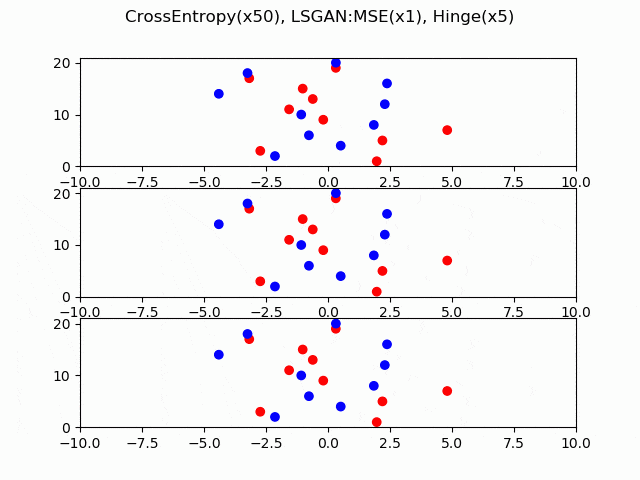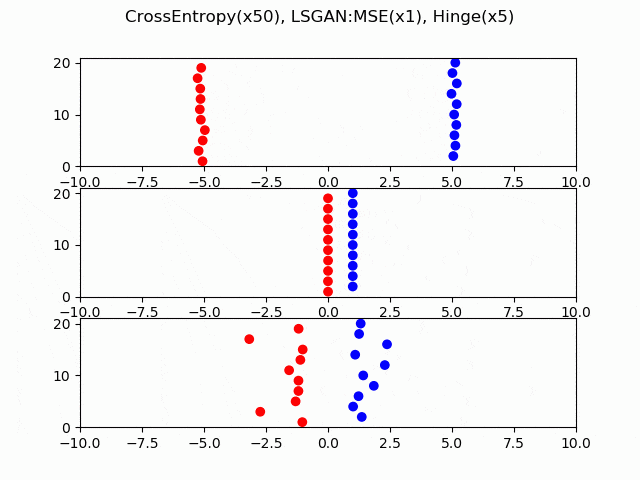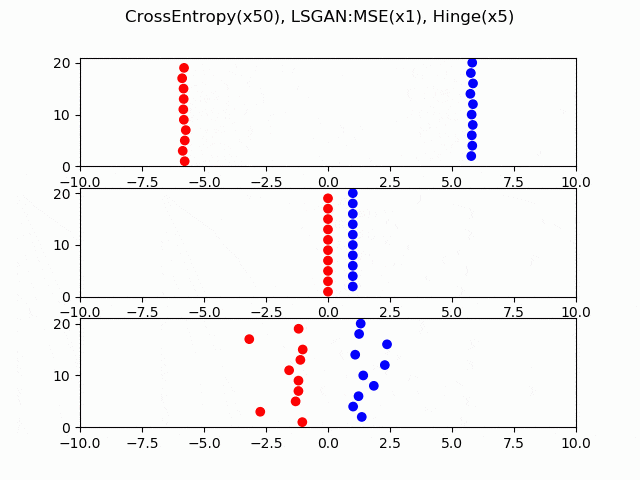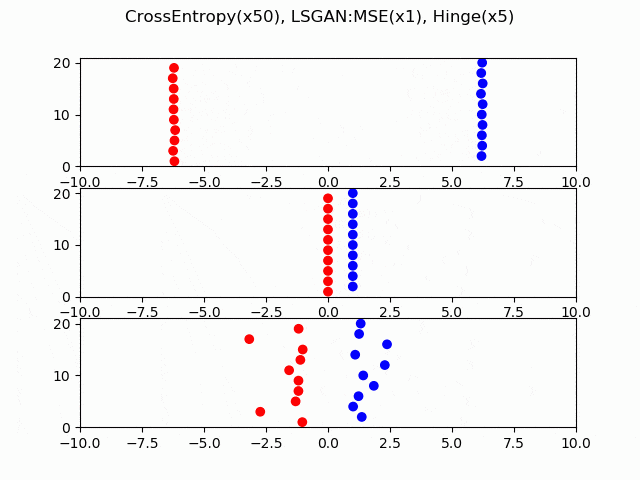
交差エントロピー、LS-GAN（平均二乗誤差）、Hingeロスについて、どのように収束していくか可視化してみました。本物と偽物のサンプルを数直線上に10個ずつ用意し、勾配降下法を適用します。見やすいようにケースごとに勾配のスケールを変えてあるので（交差エントロピーが50倍、Hingeが5倍）、どのケースが収束が速いかを考えることはできません。横軸はロジット、縦軸がサンプルのインデックスです。

ポイントは、LS-GANやHingeロスは最終的に停止しているのに対し、交差エントロピーのみRealとFakeが分離した後も差の拡大が続くということです。これはシグモイド関数の勾配が0にならないことによります。

つまり、Dが強くなりすぎる理由とは、交差エントロピーのロジットに対する微分がシグモイド関数であるため、微分係数が0にならず、Dにおける本物と偽物の乖離が永遠と大きくなるからということができます。

この部分のコードをクリックで展開

import numpy as np
import matplotlib.pyplot as plt
import os

def plot_losses():
    np.random.seed(123)
    l = np.random.rand(20) * 10 - 5
    logits = [l.copy() for i in range(3)]
    lr = 0.1
    def sigmoid(x):
        return 1.0 / (1.0 + np.exp(-x))
    if not os.path.exists("animation"):
        os.mkdir("animation")
    for i in range(100):
        gt = np.arange(20) % 2
        for j in range(3):
            if j == 0:
                # Binary Cross entropy
                grad = np.zeros(20)
                grad = ((1.0- gt) * sigmoid(logits[j]) + gt * (sigmoid(logits[j]) - 1)) * 50                
            elif j == 1:
                # LSGAN
                grad = (2*(logits[j] - gt))*1
            else:
                # Hinge
                grad = ((gt * -(logits[j] <= 1.0).astype(np.float32) + (1.0- gt) * (logits[j] >= -1.0).astype(np.float32))) * 5
            color_list = list(map(lambda x: "r" if x % 2 == 0 else "b", np.arange(20)))
            ax = plt.subplot(3, 1, j + 1)
            ax.scatter(logits[j], np.arange(20) + 1, c=color_list)
            ax.set_xlim((-10, 10))
            logits[j] -= np.clip(lr * grad, -1.0, 1.0)
        plt.suptitle("CrossEntropy(x50), LSGAN:MSE(x1), Hinge(x5)")
        plt.savefig(f"animation/{i:03}.png")
        plt.clf()

実験

DCGANで（ネットワークは微妙に変えています）、Hingeロスと交差エントロピーでInceptionスコアの比較をします。Inceptionスコアはこちらのコードを使います。

STL-10のunlabeledをDCGANでノイズから作成します。

オリジナル

Inceptionスコアは48.37でした。ISがこの値に近いほど本物並の表現ができています。

交差エントロピー、HingeロスでのInceptionスコア比較

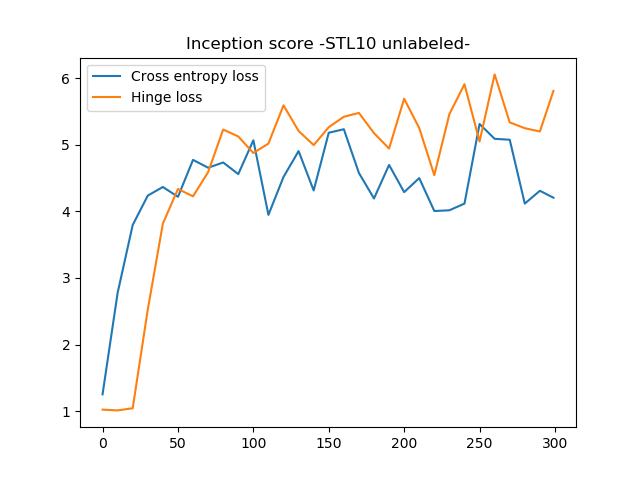
10エポックおきに記録したGの係数から、10万個サンプリングしISを比較します。

交差エントロピーのISが5前後で止まっているのに対して、Hingeロスでは6近いISを出しました。特に訓練後半部分での伸びがHingeロスのほうがいいです。

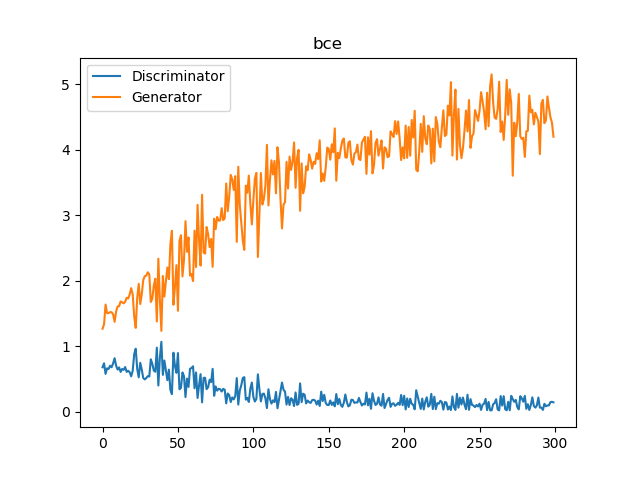
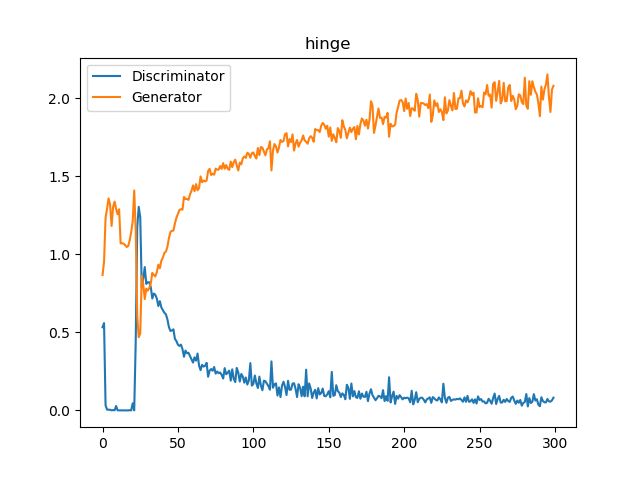
D/Gの実際の損失値をプロットしてみましょう。

上が交差エントロピーで、下がHingeです。どちらもDの損失が0近くなっていることには変わりありませんが、0近くなったときに伸びが良いのはHingeロスということができます。Hingeロスのロジットは、±1の範囲外になったときに勾配が0になるためです。

注意点

Hingeロスの有効性は示せましたが、Hingeロスのほうが交差エントロピーよりも必ず高いISを出せるとはまだいえないことには注意しましょう。今回のような交差エントロピーでロスが0近くなってしまう例ではHingeロスは有効ですが、交差エントロピーを使ってうまくいく例では、もしかすると交差エントロピーのほうが学習が速いかもしれません。今回の例でも前半の数十エポックの立ち上がりが良かったのは交差エントロピーでした。あくまで交差エントロピーでだめだったときの選択肢の一つとして持っておくとよさそうです。

マージン最大化からの視点

SVMでしばし言われるように、Hingeロスとはロジットに対するマージン最大化問題とも考えることができます。本物と偽物の間の距離を最大化し、ロジットの±1の間がマージンということになります。

交差エントロピーがロジスティクス回帰の二値分類だったことを考えると、HingeロスはSVMの線形カーネルということになります。アバウトな捉え方ですが、ロジスティクス回帰－SVMのアナロジーから考えると、画質が上がりやすいのも理解しやすいでしょう。

まとめ

GANの訓練がうまくいかない一例として、Dが強くなりすぎるケースを考えました。そのようなときに、Hingeロスを使うと交差エントロピーのときと比べて学習が進みやすくなります。

その理由は、交差エントロピーのロジットでの微分がシグモイド関数であるため、微分係数が0とならずに、永遠と本物と偽物の乖離が拡大するから、これによりDが強化されすぎてGが騙せなくなるから。一方のHingeロスは±1で微分係数が0になるので、本物と偽物の乖離は一定以上広がらないから、というのが考えられます。つまり、本物と偽物の乖離に対して上限を設けたのがHingeロスということになります。交差エントロピーは画像分類や物体検出のような、y_trueが固定値のタスクでは有効ですが、GANのように変動するタスクでは必ずしもベストではないようです。

訓練コード

クリックして展開

import torch
from torch import nn
import torchvision
import torchvision.transforms as transforms
import numpy as np
from tqdm import tqdm
import os
import pickle
import statistics
from inception_score import inception_score
import glob

def load_datasets(raw_tensor=False):
    trainset = torchvision.datasets.STL10(root="./data",
                                          split="unlabeled",
                                          download=True)
    with open("./data/stl10_binary/unlabeled_X.bin", 'rb') as f:
        unlabeled = np.fromfile(f, dtype=np.uint8).reshape(-1, 3, 96, 96).swapaxes(2, 3).astype(np.float32)
        unlabeled = (unlabeled / 127.5) - 1.0

    unlabeled = torch.as_tensor(unlabeled)
    if raw_tensor:
        return unlabeled

    # dataset
    dataset = torch.utils.data.TensorDataset(unlabeled)
    loader = torch.utils.data.DataLoader(dataset, batch_size=512, shuffle=True) # メモリ関係でマルチプロセスでバグるので使わない
    return loader

def weight_init(layer):
    if type(layer) == nn.Conv2d or type(layer) == nn.ConvTranspose2d:
        nn.init.normal_(layer.weight, 0.0, 0.02)

class Generator(nn.Module):
    def __init__(self):
        super().__init__()
        self.main = nn.Sequential(
            nn.ConvTranspose2d(128, 256, 6, 1, 0), # 6x6
            nn.BatchNorm2d(256),
            nn.ReLU(inplace=True),

            nn.ConvTranspose2d(256, 128, 2, 2, 0), # 12x12
            nn.BatchNorm2d(128),
            nn.ReLU(inplace=True),

            nn.ConvTranspose2d(128, 64, 2, 2, 0), # 24x24
            nn.BatchNorm2d(64),
            nn.ReLU(inplace=True),

            nn.ConvTranspose2d(64, 32, 2, 2, 0), # 48x48
            nn.BatchNorm2d(32),
            nn.ReLU(inplace=True),

            nn.ConvTranspose2d(32, 3, 2, 2, 0), #96x96
            nn.Tanh()
        )
        self.main.apply(weight_init)

    def forward(self, x):
        return self.main(x)

class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.model = nn.Sequential(
            nn.Conv2d(3, 32, kernel_size=3, padding=1),
            nn.BatchNorm2d(32),
            nn.LeakyReLU(0.2, inplace=True), #96x96

            nn.AvgPool2d(2),
            nn.Conv2d(32, 64, kernel_size=3, padding=1),
            nn.BatchNorm2d(64),
            nn.LeakyReLU(0.2, inplace=True), #48x48

            nn.AvgPool2d(2),
            nn.Conv2d(64, 128, kernel_size=3, padding=1),
            nn.BatchNorm2d(128),
            nn.LeakyReLU(0.2, inplace=True), #24x24

            nn.AvgPool2d(2),
            nn.Conv2d(128, 256, kernel_size=3, padding=1),
            nn.BatchNorm2d(256),
            nn.LeakyReLU(0.2, inplace=True), #12x12

            nn.AvgPool2d(2),
            nn.Conv2d(256, 512, kernel_size=3, padding=1),
            nn.BatchNorm2d(512),
            nn.LeakyReLU(0.2, inplace=True), #6x6

            nn.AvgPool2d(6),
            nn.Conv2d(512, 1, 1) # fcの代わり
        )
        self.model.apply(weight_init)

    def forward(self, x):
        return self.model(x).squeeze()

class ProbLoss(nn.Module):
    def __init__(self, opt):
        assert opt["loss_type"] in ["bce", "hinge"]
        super().__init__()
        self.loss_type = opt["loss_type"]
        self.device = opt["device"]
        self.ones = torch.ones(opt["batch_size"]).to(opt["device"])
        self.zeros = torch.zeros(opt["batch_size"]).to(opt["device"])
        self.bce = nn.BCEWithLogitsLoss()

    def __call__(self, logits, condition):
        assert condition in ["gen", "dis_real", "dis_fake"]
        batch_len = len(logits)

        if self.loss_type == "bce":
            if condition in ["gen", "dis_real"]:
                return self.bce(logits, self.ones[:batch_len])
            else:
                return self.bce(logits, self.zeros[:batch_len])
        
        elif self.loss_type == "hinge":
        # SPADEでのHinge lossを参考に実装
        # https://github.com/NVlabs/SPADE/blob/master/models/networks/loss.py        
            if condition == "gen":
                # Generatorでは、本物になるようにHinge lossを返す
                return -torch.mean(logits)
            elif condition == "dis_real":
                minval = torch.min(logits - 1, self.zeros[:batch_len])
                return -torch.mean(minval)
            else:
                minval = torch.min(-logits - 1, self.zeros[:batch_len])
                return -torch.mean(minval)


def train(loss_type):
    # モデル
    device = "cuda"
    model_G, model_D = Generator(), Discriminator()
    model_G, model_D = nn.DataParallel(model_G), nn.DataParallel(model_D)
    model_G, model_D = model_G.to(device), model_D.to(device)

    params_G = torch.optim.Adam(model_G.parameters(),
                lr=0.0002, betas=(0.5, 0.999))
    params_D = torch.optim.Adam(model_D.parameters(),
                lr=0.0002, betas=(0.5, 0.999))
    
    # ロス
    loss_func = ProbLoss({"device":device, "batch_size":512, "loss_type":loss_type})

    # エラー推移
    result = {}
    result["log_loss_G"] = []
    result["log_loss_D"] = []

    # 訓練
    dataset = load_datasets()
    for i in range(300):
        log_loss_G, log_loss_D = [], []
        for real_img in tqdm(dataset):
            real_img = real_img[0].to(device)
            batch_len = len(real_img)

            # Gの訓練
            # 偽画像を作成
            z = torch.randn(batch_len, 128, 1, 1).to(device)
            fake_img = model_G(z)

            # 偽画像を一時保存
            fake_img_tensor = fake_img.detach()

            # 偽画像を本物と騙せるようにロスを計算
            out = model_D(fake_img)
            loss_G = loss_func(out, "gen")
            log_loss_G.append(loss_G.item())

            # 微分計算・重み更新
            params_D.zero_grad()
            params_G.zero_grad()
            loss_G.backward()
            params_G.step()

            # Discriminatoの訓練
            # sample_dataの実画像
            real_img = real_img.to(device)
            # 実画像を実画像と識別できるようにロスを計算
            real_out = model_D(real_img)
            loss_D_real = loss_func(real_out, "dis_real")

            # 偽の画像の偽と識別できるようにロスを計算
            fake_out = model_D(fake_img_tensor)
            loss_D_fake = loss_func(fake_out, "dis_fake")

            # 実画像と偽画像のロスを合計
            loss_D = loss_D_real + loss_D_fake
            log_loss_D.append(loss_D.item())

            # 微分計算・重み更新
            params_D.zero_grad()
            params_G.zero_grad()
            loss_D.backward()
            params_D.step()

        result["log_loss_G"].append(statistics.mean(log_loss_G))
        result["log_loss_D"].append(statistics.mean(log_loss_D))
        print("log_loss_G =", result["log_loss_G"][-1], ", log_loss_D =", result["log_loss_D"][-1])

        # 画像を保存
        out_dir = "dcgan_stl_"+loss_type
        if not os.path.exists(out_dir):
            os.mkdir(out_dir)
        torchvision.utils.save_image(fake_img_tensor[:min(batch_len, 100)],
                                f"{out_dir}/epoch_{i:03}.png", normalize=True, range=(-1.0, 1.0))

        # モデルの保存
        if not os.path.exists(f"{out_dir}/models"):
            os.mkdir(f"{out_dir}/models")
        if i % 10 == 0 or i == 299:
            torch.save(model_G.state_dict(), f"{out_dir}/models/gen_{i:03}.pytorch")                        
            torch.save(model_D.state_dict(), f"{out_dir}/models/dis_{i:03}.pytorch")                        

    # ログの保存
    with open(f"{out_dir}/logs.pkl", "wb") as fp:
        pickle.dump(result, fp)

def original_inception_score():
    dataall = load_datasets(raw_tensor=True)

    print("Original inception score")
    print(inception_score(dataall, batch_size=64, resize=True, splits=10))
    # (48.3742330621847, 0.5271509872196527)

def plot_original():
    dataall = load_datasets(raw_tensor=True)
    torchvision.utils.save_image(dataall[:100], "stl10.png", normalize=True, padding=5, nrow=10)


def sampling_inception_score(loss_type):
    result = []
    for path in tqdm(sorted(glob.glob("dcgan_stl_" + loss_type + "/models/gen*"))):
        model = Generator()
        model = model.to("cuda")
        model = torch.nn.DataParallel(model)
        model.load_state_dict(torch.load(path))
        infer = [model(torch.randn(500, 128, 1, 1).to("cuda")).to("cpu").detach() for i in range(200)]
        infer = torch.cat(infer, dim=0)
        iscore = inception_score(infer, cuda=True, batch_size=64, resize=True, splits=10)
        result.append(path.replace("\\", " / ")+"\t"+str(iscore))
    with open("result_" + loss_type + ".txt", "w") as fp:
        fp.write("\n".join(result))

if __name__ == "__main__":
    train("hinge")

1. Dのロスが0ではなく、Gのロスが0になってしまうケースは直感的には「モード崩壊」（同一の画像を生成してしまう現象）になるかと思われますが、Gのロスが0＝モード崩壊の理論的な根拠付けが調べてもよくわかりませんでした。もしここらへんの理由付けをご存知の方がいらっしゃったらぜひ教えてください。 ↩