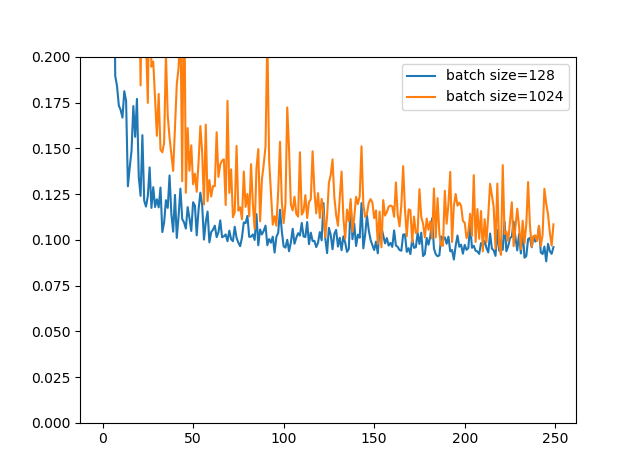
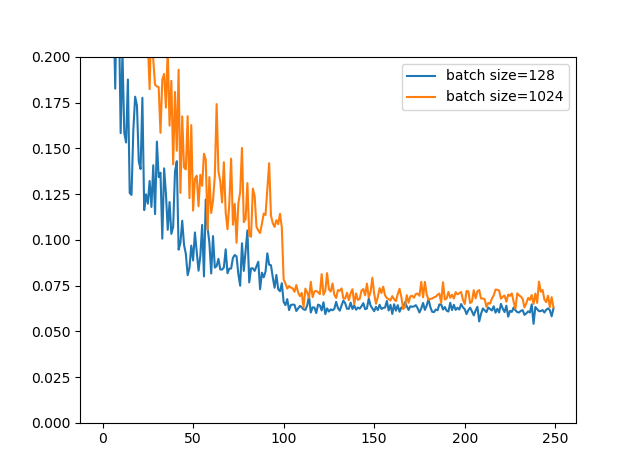
前回の記事で「BC-Learningは大きなバッチサイズで再現できなかった」と書きましたが、Google Brainが出した論文を参考にしたら、大きなバッチサイズでも精度を出すことに成功しました。秘訣は学習率の調整にありました。
BC-Learningの結果まとめ
前回の記事からの続きです。バッチサイズ128では論文通りの精度を出すことができました。
| case | BC-Learning | Batch size | Step size | LR-Decay | Standard DA | Test acc |
|---|---|---|---|---|---|---|
| 0 | No | 128 | - | No | No | 0.8935 |
| 1 | Yes | 128 | 128 | No | No | 0.9118 |
| 2 | Yes | 1024 | 128 | No | No | 0.9074 |
| 3 | Yes | 1024 | 1024 | No | No | 0.8985 |
| 4 | Yes | 128 | 128 | Yes | No | 0.9173 |
| 5 | Yes | 128 | 128 | Yes | Yes | 0.9459 |
- BC-Learningについては前回の記事参照。簡単に言うと2枚の異なるクラスの画像を足し合わせるData Augmentation
- Batch sizeとStep sizeの違いは、Batch sizeはニューラルネットワークに食わせるミニバッチ1回あたりのサンプル。Step sizeは1回のミニバッチで使うベースとなる画像の数。例えば、Batch sizeが1024で、Step sizeが128なら、1枚の画像に対して残りの127枚のうち異なるクラスの画像を8枚選び、合成画像を8枚作るという操作を表す。
- LR-Decayは学習率減衰。Adamのオプティマイザーで1e-3の初期学習率に対し、100エポック、150エポック、200エポックで学習率をそれぞれ1/5にする。
- Standard DAは水平反転、上下左右の4クロップ
前回の要点は、バッチサイズ128では論文の通りの精度が出たが、バッチサイズ1024のような大きなバッチサイズでは精度が出なかったという点です。今回、これを解消します。やり方はありました。
一様分布の乱数を疑う
まず自分が疑ったのは、BC-Learningの一様乱数でした。ここでの乱数とは、2つの画像を混ぜ合わせるときに、
$$rx_1+(1-r)x_2 $$
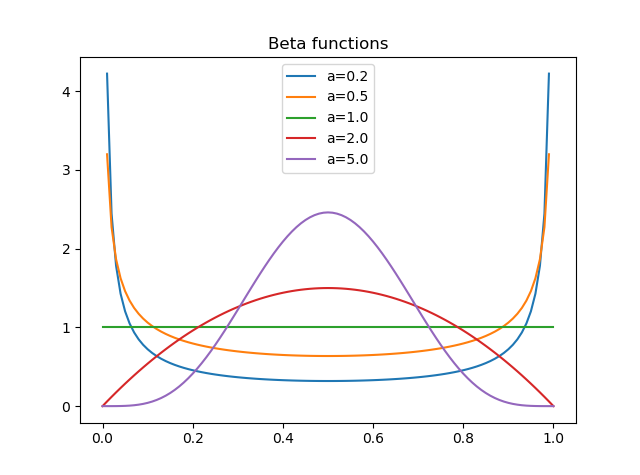
という式での$r$です。BC-Learningではこの$r$を一様乱数で定義していました。ただし、一様乱数はベータ分布$Be(a,b)$の$a=b=1$の特別な場合なので、ほぼ同じような補間をしてかつベータ分布の乱数を使っているMixupのほうが拡張性あって、まだ可能性がありそうだからと思ったからです。
学習率を変えずにバッチサイズを1024にして(この記事ではbatch size=step sizeとするので、同一のものと考えてOKです)、乱数のみベータ分布$Be(\alpha, \alpha)$にしたときのテスト精度は次のようになります。alpha=1のときは一様分布です。
| alpha | Test acc |
|---|---|
| 0.25 | 0.9077 |
| 0.5 | 0.9078 |
| 0.75 | 0.9102 |
| 1 | 0.9071 |
| 1.5 | 0.9067 |
| 2 | 0.9082 |
| 2.5 | 0.9069 |
| 3 | 0.9027 |
| 4 | 0.9025 |
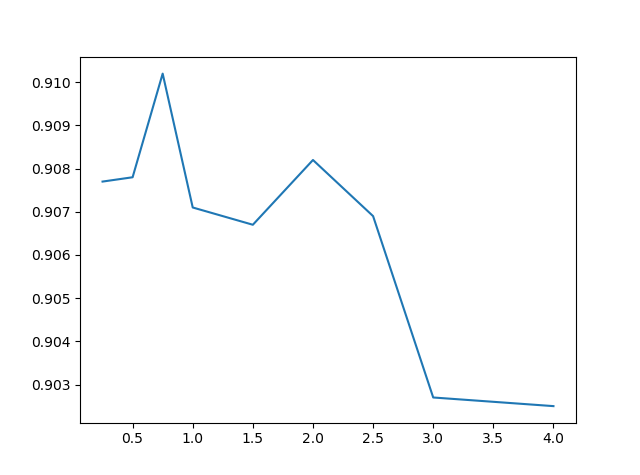
学習率が高すぎるという状況を回避するために、学習率の減衰は入れています。バッチサイズ128のときと同様、Adamのオプティマイザーで初期学習率を1e-3とし、100、150、200エポックでそれぞれ学習率を1/5にしました。引き続き、TensorFlow・KerasのTPUで訓練させています。
ちなみにバッチサイズ128のときの同条件の精度は0.9173でした。ちょっと低すぎるような気がします。
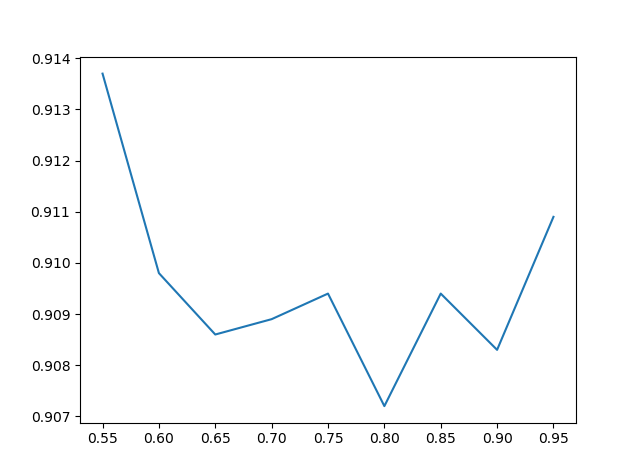
なんとなくα=0.5~1のあたりにスイートスポットがありそうな気がしますね。0.55~0.95まで同じ条件で細かく(0.05刻みで)見てみましょう。別に調べました。
確かに0.55は高いけどノイズ挙動だよねという感は否めません。なので、おそらく確率を第一に疑うのは間違いでしょう。ベータ分布の値を3、4と大きくしたときは明らかに落ちているので、確率はチューニングの余地があるのは否定はしません。しかし、疑うべきは学習率です。
Googleの論文を参考に
大きなバッチサイズに対して精度を出す方法を探していたらこんな論文を見つけました。
Don't Decay the Learning Rate, Increase the Batch Size
https://arxiv.org/abs/1711.00489
Google Brainが2017年に出した論文で、非常に面白い内容です。詳しい内容はまたの機会に別記事で書く予定ですが、簡単に言うと、勾配法のブレ$g$(最適化しているときの精度やロスのノイズだと考えてOKでしょう)は、
$$g=\epsilon(\frac{N}{B}-1)\tag{1}$$
で表されるということです。ここで$\epsilon$は学習率、$N$はサンプル数、$B$はバッチサイズを表します。うまく精度が出ないということは、勾配法のブレ$g$が最適な値ではないということを意味します。
これは裏を返せば、あるバッチサイズで良い精度が出ているときに、バッチサイズを変えて同じ精度を出すために、バッチサイズと学習率の関係式が存在するということを意味します。具体的には$g$を同一にすればいいので、$N$が$B$に対して十分大きいとき(具体的には論文では$N$が$B$の10倍まで)、バッチサイズを2倍にしたとき学習率も2倍にすれば、$g$は変わらずに同一の精度が出るだろうということです。ただし、あまりに(初期)学習率を大きくすると精度が落ちることもあるので、際限なく大きくできるわけではないそうです。
バッチサイズが128のときに初期学習率が1e-3でうまくいきました。つまり、バッチサイズを1024にするというのは$B$が8倍になっているので、**初期学習率も8倍にして8e-3にすればいいのではないか?**という発想が得られます。これは実際成功します。それを見ていきましょう。
初期学習率を8倍にする
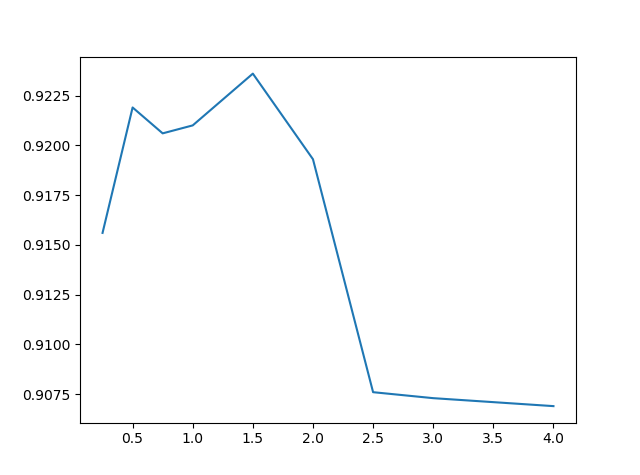
(1)式を参考に、初期学習率を8倍にして当たりをつけます。学習率減衰は入れたままで100, 150, 200エポックで同様に割ります(最初が8e-3なので、1.6e-3→3.2e-4→…というような学習率推移になります)。
| alpha | Test acc |
|---|---|
| 0.25 | 0.9156 |
| 0.5 | 0.9219 |
| 0.75 | 0.9206 |
| 1 | 0.9210 |
| 1.5 | 0.9236 |
| 2 | 0.9193 |
| 2.5 | 0.9076 |
| 3 | 0.9073 |
| 4 | 0.9069 |
自分「すごい精度出てる!!Googleの論文すげえ!!」
ちなみに同条件でのバッチサイズ128の場合の精度は0.9173でした。
乱数のパラメーターαは0.5~1.5あたりにスイートスポットがあるのがわかります。オリジナルのBC-Learningのように一様分布(α=1)でやっても悪くないですが、チューニングしても構わない値といえるでしょう。
他の条件でもバッチサイズを1024にする
乱数のパラメーターはいじらずに、BC-Learningと同じく一様乱数に戻します。
学習率減衰を入れないパターンと、学習率減衰を入れてStandard DataAugmentationを入れたパターンを確かめます。
学習率減衰を入れないパターン(バッチサイズ128では91.18%)
学習率減衰を入れずに初期の学習率一本で勝負する場合です。バッチサイズ128では91.18%でしたが、**バッチサイズ1024・学習率8e-3では90.82%**となりました。
ちょっとブレが大きいですね。あくまであの式は目安なので当たりをつけるにはいいでしょうが、細かなチューニングをするともう少し精度は上がると思います。しかし、バッチサイズ1024でも0.2~0.3%差になったのは評価すべきでしょう。
学習率減衰+Standard Data Augmentation(バッチサイズ128では94.59%)
今度はStandard Data Augmentationを入れて完全装備で行きます。バッチサイズでは94.59%もの精度が出ましたが、**バッチサイズ1024では93.78%**を出すことができました。
精度面では0.8%程度の劣化ですが、学習曲線を見ているとそこまで悪くはないような印象を受けます。最後の方は割とガチャな感じあるので。
ちなみに、Googleの論文では(バッチサイズ128・初期学習率0.1でCIFAR-10をモメンタムオプティマイザーで訓練したとときに)、初期学習率が0.4を超えてくると(1)式を使っても精度面での劣化が出てくるとありました。したがって、バッチサイズが128の4倍以上もある「1024」という設定では、精度面での劣化が出ても仕方がないと思われます。
もちろん、確率や細かい初期学習率のチューニングをすればもう少しマシな精度は出ると思います(初期学習率8e-3、ベータ分布の0.5の確率にすると、バッチサイズ1024でも93.96%までは上げられました)。しかし、学習率のチューニングで当たりをつける際に(1)の式はかなり有用に機能するというのが確認できました。学習率はハイパーパラメータの中で最も重要な値と思われるので、これの当たりがつけられるというのはかなり嬉しいです。
まとめ
- Googleの論文を参考にしたら、大きなバッチサイズでもBC-Learningである程度の精度を出すことができた
- 起点となるバッチサイズに比例して、初期の学習率を定数倍するだけでかなり当たりに近づく
- 分布の乱数のチューニングも効果はあるが、学習率のチューニングのほうがおそらく効きが大きい
ということでした。これでめでたしめでたしですね。