ambisonicsシミュレーション Python

高次アンビソニックスについて

アンビソニックスとはある受音点に入射する音波の到来方向すなわち音波の入射指向性を再現することで立体的な音響再生を実現する手法です。ある点に入射する音波の三次元の指向特性を球面調和関数により、展開し再生時に展開された指向特性を再現するようにスピーカアレイの各スピーカの出力を決定することで入射指向性を再現するもので0次と1次に注目したものをアンビソニックスと呼ばれ、2次以上の球面調和関数も用いるものを高次アンビソニックスと呼ばれています。

今回の記事ではマイクロホンで収音し、その後仮想的にスピーカーを配置し、音場再現するといった流れのコードを記載します。

シミュレーションに用いる波について

今回の記事で書くシミュレーションでは平面波しか扱いませんが平面波・球面波・指向性球面波の3つがあります。
それぞれのデカルト座標系での波の式は次のように書くことができます。
$$e^{i\vec{k_i}\vec{r}}$$
$$\frac{e^{ik|r-r_s|}}{4\pi|r-r_s|}$$
$$\frac{e^{ik|r-r_s|}}{4\pi|r-r_s|}\Bigl(\alpha-\bigl(1-\alpha\bigr)\bigl(1+\frac{i}{k|r-r_s|}\bigr)\cos\gamma\Bigr)$$
$\gamma$は受音位置と音源位置のベクトルの角度、$\alpha$は指向性係数($\alpha$=1で球面波と一致)です。
次に極座標系でのそれぞれの波の式は次のように書くことができます。
$$e^{i\vec{k_i}\vec{r}} = \sum_{n=0}^\infty\sum_{m=-n}^n4\pi i^n j_n(kr) Y_n^m(\theta,\varphi) Y_n^m(\theta_i,\varphi_i)^*$$

$$\frac{e^{ik|r-r_s|}}{4\pi|r-r_s|} = \sum_{n=0}^\infty\sum_{m=-n}^n ik j_n(kr) h_n(kr_s) Y_n^m(\theta,\varphi) Y_n^m(\theta_s,\varphi_s)^*$$

$$\frac{e^{ik|r-r_s|}}{4\pi|r-r_s|}\Bigl(\alpha-\bigl(1-\alpha\bigr)\bigl(1+\frac{i}{k|r-r_s|}\bigr)\cos\gamma\Bigr) = \sum_{n=0}^\infty\sum_{m=-n}^n k j_n(kr)[i\alpha h_n(kr_s) +(1-\alpha)h_n^{'}(kr_s)]Y_n^m(\theta,\varphi) Y_n^m(\theta_s,\varphi_s)^*$$

$j_n(kr)$は第一種球ベッセル関数、$h_n(kr)$は第一種ハンケル関数です。$^*$は複素共軛転置を表します。

green_function.py

import numpy as np 
import function as fu


def Plane_wave(freq,cv, pos_s,vec_dn, pos_r):
    # freq: frequency
    # cv: sound speed
    # pos_s: source position (Not used in this function)
    # vec_dn: plane wave direction vector
    # pos_r: receiver position
    omega = 2*np.pi*freq
    k = omega/cv
    vec_dn_unit = np.array([0]*3,dtype = 'float')
    vec_dn_unit[0] = vec_dn[0] / np.linalg.norm(vec_dn, ord=2)
    vec_dn_unit[1] = vec_dn[1] / np.linalg.norm(vec_dn, ord=2)
    vec_dn_unit[2] = vec_dn[2] / np.linalg.norm(vec_dn, ord=2)
    azi,ele,_ = fu.cart2sph(-vec_dn_unit[0],-vec_dn_unit[1],-vec_dn_unit[2])
    ele_1 = np.pi / 2 - ele
    kx = k * np.cos(azi) * np.sin(ele_1)
    ky = k * np.sin(azi) * np.sin(ele_1)
    kz = k * np.cos(ele_1)
    x = pos_r[0] - pos_s[0]
    y = pos_r[1] - pos_s[1]
    z = pos_r[2] - pos_s[2]
    ret = np.exp(1j*(kx*x + ky*y + kz*z))
    return ret

def green(freq, cv, vec1, vec2):
    vec = np.array([0]*3,dtype = 'float')
    vec[0] = vec1[0] - vec2[0] 
    vec[1] = vec1[1] - vec2[1]
    vec[2] = vec1[2] - vec2[2]
    rr = np.linalg.norm(vec, ord=2)
    omega = 2 * np.pi * freq
    k = omega / cv
    jkr = 1j * k * rr
    ret = np.exp(jkr)/(4 * np.pi * rr)
    return ret

def green2(alpha, freq, cv, vecrs, vecr):
    # alpha:directivity coefficient 0~1 
    #                               0   :dipole 
    #                               0.5 :cardiod 
    #                               1   :monopole
    # CV: sound speed
    # freq: frequency [Hz] (can be vector)
    # vecrs: sound source position
    # vecr: receiver position
    vecrd = np.array([0]*3,dtype = 'float')
    vecrd[0] = vecrs[0] - vecr[0]
    vecrd[1] = vecrs[1] - vecr[1]
    vecrd[2] = vecrs[2] - vecr[2]
    rd = np.linalg.norm(vecrd, ord=2)
    omega = 2 * np.pi * freq
    k = omega/cv
    cosgamma = np.dot(vecrd,-vecrs) / (np.linalg.norm(vecrd, ord=2) * np.linalg.norm(vecrs, ord=2))
    ret = green(freq, cv, vecrs, vecr) * (alpha - (1 - alpha)*(1 + (1j/(k*rd)))*cosgamma)
    return ret

アンビソニックスで主に使う関数などは以下にまとめてます。

function.py

import scipy as sp
from scipy.special import sph_harm
import numpy as np
from scipy.special import spherical_jn
from scipy.special import spherical_yn
from numpy import arctan2, sqrt
import numexpr as ne

def cart2sph(x,y,z):
    """ x, y, z :  ndarray coordinates
        ceval: backend to use: 
              - eval :  pure Numpy
              - numexpr.evaluate:  Numexpr """

    azimuth = ne.evaluate('arctan2(y,x)')
    xy2 = ne.evaluate('x**2 + y**2')
    elevation = ne.evaluate('arctan2(z, sqrt(xy2))')
    r = eval('sqrt(xy2 + z**2)')
    return azimuth, elevation, r

def EquiDistSphere(n):
    golden_angle = np.pi * (3 - np.sqrt(5))
    theta = golden_angle * (np.arange(n)+1)
    z = np.linspace(1 - 1.0 / n, 1.0 / n - 1, n)
    radius = np.sqrt(1 - z * z)

    points = np.zeros((n, 3))
    points[:,0] = radius * np.cos(theta)
    points[:,1] = radius * np.sin(theta)
    points[:,2] = z
    return points

def BnMat2(N,k,r):
    B = np.zeros((N+1)**2, dtype = np.complex).reshape((N+1)**2,)
    dx = 0
    for i in range(N+1):
        A = Bn2(i,k,r)
        for j in np.arange(-i,i+1,1):
            B[dx] = A
            dx +=1
    return B

def Bn2(n,k,r):
    kr = k*r
    y = 4 * np.pi * (1j**(n)) * spherical_jn(n,kr)
    return y
def calcSH(N,azi,ele):
    y_n = np.array([],dtype = np.complex)
    for n in range(N+1):
        for m in np.arange(-n,n+1,1):
            y_n = np.append(y_n,sph_harm(m,n,azi,ele))
    return y_n

def encode(ambi_order, azi, ele,k,r, mic_sig):
    Y_N = np.zeros((len(azi),(ambi_order+1)**2),dtype = np.complex)
    for i in range(azi.size):
        Y_N[i,:] = calcSH(ambi_order, azi[i],ele[i])
    invY = np.linalg.pinv(Y_N)             
    Wnkr = BnMat2(ambi_order,k,r)
    ambi_signal = np.diag(1/Wnkr) @ invY @ mic_sig
    return ambi_signal

def decode(ambi_order, azi, ele,r,lambda_,ambi_signal):
    Y_N = np.zeros((len(azi),(ambi_order+1)**2),dtype = np.complex)
    for i in range(azi.size):
        Y_N[i,:] = calcSH(ambi_order, azi[i],ele[i])
    invY = np.linalg.pinv(np.conj(Y_N.T)) 
    r_res = r % lambda_
    spkr_output = np.exp(1j*(2*np.pi*r_res/lambda_)) * (invY @ ambi_signal)
    return spkr_output

アンビソニックス(内部問題ver)

球面上の任意の位置の音圧を次のように表すことができます。

$$p\bigl(\theta,\varphi,r,\omega\bigr) = \sum_{n=0}^\infty\sum_{m=-n}^n A_{nm} W_{nkr} Y_n^m(\theta,\varphi) $$

$A_{nm}$は展開係数(アンビソニックス係数)、$W_{nkr}$はマイクロホンの形状(今回のシミュレーションでは中空アレイを使用)です。アンビソニックスはエンコードとデコードの2つの処理を行います。まずエンコードより展開係数を求め、デコードでスピーカーより出力する駆動信号を求めます。

エンコード

展開係数$A_{nm}$を求めます。以降の式は行列で表していきます。
$$A_{nm}= diag(\frac{1}{W_{nkr}}) * Y_n^m(\theta,\varphi)^+ * p\bigl(\theta,\varphi,r,\omega\bigr) $$

より展開係数を求めることができます。$^+$は一般化逆行列を表します。ここで問題なのが$W_{nkr}$で割っているため$W_{nkr}$が0になる周波数では波が再現されない禁止周波数の問題があります。この禁止周波数の問題を回避するために剛球アレイや中空カーディオイドアレイなどのマイクロホンアレイが考えられています。

以下のコードではまず一次音源(再生したい音場)をマイクロホンの配置、収音、エンコードまでの流れを書いてます。
マイクロホンの配置は以下の記事より球面に均等に配置するものを扱っています。

blog.marmakoide.org/?p=1

~encode.py

import green_function as gr
import  function as fu
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.cm as cm

#初期条件
ambi_order = 7              #打ち切り次数
freq = 550                  #周波数
pos_s = np.array([2,0,0])   #一次音源の座標x,y,z
vec_dn = np.array([1,0,0])  #平面波の向き
cv = 344                    #音速
r_sp = 1.5                  #スピーカーを配置する半径
r_mic = 0.05                #マイクロホンの半径
#グラフ条件
Plot_range = 2.0
space = 0.05

#計算
lambda_ = cv/freq
omega = 2*np.pi*freq
k = omega/cv


#スピーカー配置を決定
num_sp = (ambi_order+1)**2
xyz = fu.EquiDistSphere((ambi_order+1)**2)
xyz = np.array([xyz]).reshape(num_sp,3)

pos_sp = xyz * r_sp

azi_sp, ele_sp, rr_sp = fu.cart2sph(pos_sp[:,0],pos_sp[:,1],pos_sp[:,2])
ele_sp1 = np.pi /2 - ele_sp
#マイク配置を決定
num_mic = (ambi_order+1)**2
pos_mic = xyz * r_mic
azi_mic, ele_mic, rr_mic = fu.cart2sph(pos_mic[:,0],pos_mic[:,1],pos_mic[:,2])
ele_mic1 = np.pi /2 - ele_mic
#収音
mic_sig = np.array([])
for i in range(num_mic):
    mic_sig_ = gr.Plane_wave(freq,cv,pos_s,vec_dn,pos_mic[i])
    mic_sig = np.append(mic_sig, mic_sig_)

encode.py

#エンコード
ambi_signal = fu.encode(ambi_order,azi_mic,ele_mic1,k,r_mic,mic_sig)
"""
def encode(ambi_order, azi, ele,k,r, mic_sig):
    Y_N = np.zeros((len(azi),(ambi_order+1)**2),dtype = np.complex)
    for i in range(azi.size):
        Y_N[i,:] = calcSH(ambi_order, azi[i],ele[i])
    invY = np.linalg.pinv(Y_N)             
    Wnkr = BnMat2(ambi_order,k,r)
    ambi_signal = np.diag(1/Wnkr) @ invY @ mic_sig
    return ambi_signal
"""

デコード

スピーカーからの展開係数とエンコードで求めた展開係数を一致させる処理を行います。具体的には以下の式です。

$$A_{nm}= Y_n^m(\theta,\varphi)^* * w_l $$

$w_l$は駆動信号です。この式より

$$w_l= Y_n^m(\theta,\varphi)^{*^{+}} * A_{nm} $$

より駆動信号を求めることができます。このデコードでは一次音源と２次音源が平面波の場合のみ一致しますが位相について考えるとこの式では一致しない場合があります。位相のズレも考えたデコードの式は以下の式になります。
$$r_{res} \equiv mod(r_{sp},\lambda)$$
$$w_l= e^{i\bigl(\frac{2\pi r_{res}}{\lambda}\bigr)}\times Y_n^m(\theta,\varphi)^{*^{+}} * A_{nm} $$

他の波を再現する場合は以下の式を用います。

$$w_l= Y_n^m(\theta,\varphi)^{*^{+}} * diag(\frac{1}{F_{nkr}}) * A_{nm} $$

$F_{nkr}$は波により決定する値になります。

以下のコードではエンコードで求めた展開係数から駆動信号を求め、駆動信号を求めます。

decode.py

#デコード
spkr_output = fu.decode(ambi_order,azi_sp,ele_sp1,r_sp,lambda_,ambi_signal)
"""
def decode(ambi_order, azi, ele,r,lambda_,ambi_signal):
    Y_N = np.zeros((len(azi),(ambi_order+1)**2),dtype = np.complex)
    for i in range(azi.size):
        Y_N[i,:] = calcSH(ambi_order, azi[i],ele[i])
    invY = np.linalg.pinv(np.conj(Y_N.T)) 
    r_res = r % lambda_
    spkr_output = np.exp(1j*(2*np.pi*r_res/lambda_)) * (invY @ ambi_signal)
    return spkr_output
"""

グラフについて

グラフには正規化誤差と呼ばれる。次の式を用います。
$$ N_E(r,\omega) = 10\log_{10}\frac{{|p_{rep}(r,\omega)-p_{des}(r,\omega)|}^2}{{|p_{des}(r,\omega)|}^2} $$

$p_{rep}(r,\omega)$は再現音場での音圧、$p_{des}(r,\omega)$は一次音源の音場つまり所望音場での音圧です。
また、再現誤差が4%以下である領域のスイートスポットのエリアを表す半径を次の式から求めることができます。

$$ r = \frac{c}{2 \pi f}N $$

$c$は音速、$f$は周波数、$N$は打ち切り次数を表します。打ち切り次数は一般的には$floor(\sqrt{スピーカー数orマイクの数})-1$とされています。$floor(\sqrt{スピーカー数orマイクの数})-2$にしたりすることもあります。収音と再生で別々の次数を用いることが可能です。今回のシミュレーションでは一致させております。

plot.py

X = np.arange(-Plot_range,Plot_range+space,space)
Y = np.arange(-Plot_range,Plot_range+space,space)
XX,YY = np.meshgrid(X,Y)
P_org = np.zeros((X.size,Y.size), dtype = np.complex)
P_HOA = np.zeros((X.size,Y.size), dtype = np.complex)
for j in range(X.size):
    for i in range(Y.size):
        pos_r = np.array([X[j],Y[i],0])
        P_org[i,j] = gr.Plane_wave(freq,cv,pos_s,vec_dn,pos_r)
        for l in range(num_sp):
            G_transfer = gr.Plane_wave(freq,cv,pos_sp[l,:],-pos_sp[l,:],pos_r)
            P_HOA[i,j] += G_transfer *  spkr_output[l]

NE = np.zeros((X.size,Y.size), dtype = np.complex)
for i in range(X.size):
    for j in range(Y.size):
        NE[i,j] = 10*np.log10(((np.abs(P_HOA[i,j]-P_org[i,j]))**2)/((np.abs(P_org[i,j]))**2))

#スイートスポット
rad = (ambi_order*cv)/(2*np.pi*freq)

#グラフ
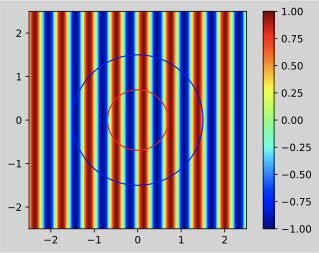
#所望音場
sweet_spot = patches.Circle(xy=(0, 0), radius=rad, ec='r',fill=False)
r_sp_ = patches.Circle(xy=(0, 0), radius=r_sp, ec='b',fill=False)
plt.figure()
ax = plt.axes()
im = ax.imshow(np.real(P_org), interpolation='gaussian',cmap=cm.hot,origin='lower', 
               extent=[-Plot_range, Plot_range, -Plot_range, Plot_range],
               vmax=1, vmin=-1)
ax.grid(False)
ax.add_patch(sweet_spot)
ax.add_patch(r_sp_)
plt.axis('scaled')
ax.set_aspect('equal')
plt.colorbar(im)
plt.savefig('original_sound.pdf',bbox_inches="tight",dpi = 64,
            facecolor = "lightgray", tight_layout = True) 
plt.show()

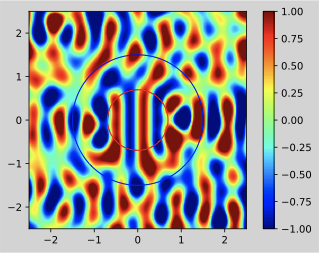
#再現音場
sweet_spot = patches.Circle(xy=(0, 0), radius=rad, ec='r',fill=False)
r_sp_ = patches.Circle(xy=(0, 0), radius=r_sp, ec='b',fill=False)
plt.figure()
ax2 = plt.axes()
im2 = ax2.imshow(np.real(P_HOA), interpolation='gaussian',cmap=cm.hot,origin='lower', 
               extent=[-Plot_range, Plot_range, -Plot_range, Plot_range],
               vmax=1, vmin=-1)
ax2.grid(False)
ax2.add_patch(sweet_spot)
ax2.add_patch(r_sp_)
plt.axis('scaled')
ax2.set_aspect('equal')
plt.colorbar(im2)
plt.savefig('reproduced_sound.pdf',bbox_inches="tight",dpi = 64,
            facecolor = "lightgray", tight_layout = True)
plt.show()

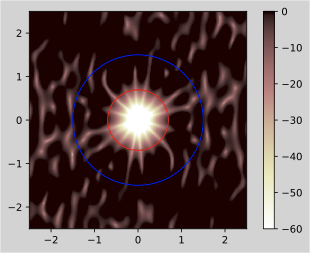
#正規化誤差
sweet_spot = patches.Circle(xy=(0, 0), radius=rad, ec='r',fill=False)
r_sp_ = patches.Circle(xy=(0, 0), radius=r_sp, ec='b',fill=False)
plt.figure()
ax3 = plt.axes()
im3 = ax3.imshow(np.real(NE), interpolation='gaussian',cmap=cm.pink,origin='lower', 
               extent=[-Plot_range, Plot_range, -Plot_range, Plot_range],
               vmax=0, vmin=-60)
ax3.grid(False)
ax3.add_patch(sweet_spot)
ax3.add_patch(r_sp_)
plt.axis('scaled')
ax3.set_aspect('equal')
plt.colorbar(im3)
plt.savefig('normalization_error.pdf',bbox_inches="tight",dpi = 64,
            facecolor = "lightgray", tight_layout = True)
plt.show()

結果

それぞれの音場の結果です。
所望音場

再現音場

正規化誤差

ambisonics.py

import green_function as gr
import  function as fu
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
import matplotlib.cm as cm

#初期条件
ambi_order = 7              #打ち切り次数
freq = 550                  #周波数
pos_s = np.array([2,0,0])   #一次音源の座標x,y,z
vec_dn = np.array([1,0,0])  #平面波の向き
cv = 344                    #音速
r_sp = 1.5                  #スピーカーを配置する半径
r_mic = 0.05                #マイクロホンの半径
#グラフ条件
Plot_range = 2.0
space = 0.05

#計算
lambda_ = cv/freq
omega = 2*np.pi*freq
k = omega/cv


#スピーカー配置を決定
num_sp = (ambi_order+1)**2
xyz = fu.EquiDistSphere((ambi_order+1)**2)
xyz = np.array([xyz]).reshape(num_sp,3)

pos_sp = xyz * r_sp

azi_sp, ele_sp, rr_sp = fu.cart2sph(pos_sp[:,0],pos_sp[:,1],pos_sp[:,2])
ele_sp1 = np.pi /2 - ele_sp
#マイク配置を決定
num_mic = (ambi_order+1)**2
pos_mic = xyz * r_mic
azi_mic, ele_mic, rr_mic = fu.cart2sph(pos_mic[:,0],pos_mic[:,1],pos_mic[:,2])
ele_mic1 = np.pi /2 - ele_mic
mic_sig = np.array([])
for i in range(num_mic):
    mic_sig_ = gr.Plane_wave(freq,cv,pos_s,vec_dn,pos_mic[i])
    mic_sig = np.append(mic_sig, mic_sig_)
#エンコード
ambi_signal = fu.encode(ambi_order,azi_mic,ele_mic1,k,r_mic,mic_sig)

#デコード
spkr_output = fu.decode(ambi_order,azi_sp,ele_sp1,r_sp,lambda_,ambi_signal)

#所望音場(一次音源)と再現音場を求める
X = np.arange(-Plot_range,Plot_range+space,space)
Y = np.arange(-Plot_range,Plot_range+space,space)
XX,YY = np.meshgrid(X,Y)
P_org = np.zeros((X.size,Y.size), dtype = np.complex)
P_HOA = np.zeros((X.size,Y.size), dtype = np.complex)
for j in range(X.size):
    for i in range(Y.size):
        pos_r = np.array([X[j],Y[i],0])
        P_org[i,j] = gr.Plane_wave(freq,cv,pos_s,vec_dn,pos_r)
        for l in range(num_sp):
            G_transfer = gr.Plane_wave(freq,cv,pos_sp[l,:],-pos_sp[l,:],pos_r)
            P_HOA[i,j] += G_transfer *  spkr_output[l]
#正規化誤差
NE = np.zeros((X.size,Y.size), dtype = np.complex)
for i in range(X.size):
    for j in range(Y.size):
        NE[i,j] = 10*np.log10(((np.abs(P_HOA[i,j]-P_org[i,j]))**2)/((np.abs(P_org[i,j]))**2))

#スイートスポット
rad = (ambi_order*cv)/(2*np.pi*freq)

#グラフ
#所望音場
sweet_spot = patches.Circle(xy=(0, 0), radius=rad, ec='r',fill=False)
r_sp_ = patches.Circle(xy=(0, 0), radius=r_sp, ec='b',fill=False)
plt.figure()
ax = plt.axes()
im = ax.imshow(np.real(P_org), interpolation='gaussian',cmap=cm.hot,origin='lower', 
               extent=[-Plot_range, Plot_range, -Plot_range, Plot_range],
               vmax=1, vmin=-1)
ax.grid(False)
ax.add_patch(sweet_spot)
ax.add_patch(r_sp_)
plt.axis('scaled')
ax.set_aspect('equal')
plt.colorbar(im)
plt.savefig('original_sound.pdf',bbox_inches="tight",dpi = 64,
            facecolor = "lightgray", tight_layout = True) 
plt.show()

#再現音場
sweet_spot = patches.Circle(xy=(0, 0), radius=rad, ec='r',fill=False)
r_sp_ = patches.Circle(xy=(0, 0), radius=r_sp, ec='b',fill=False)
plt.figure()
ax2 = plt.axes()
im2 = ax2.imshow(np.real(P_HOA), interpolation='gaussian',cmap=cm.jet,origin='lower', 
               extent=[-Plot_range, Plot_range, -Plot_range, Plot_range],
               vmax=1, vmin=-1)
ax2.grid(False)
ax2.add_patch(sweet_spot)
ax2.add_patch(r_sp_)
plt.axis('scaled')
ax2.set_aspect('equal')
plt.colorbar(im2)
plt.savefig('reproduced_sound.pdf',bbox_inches="tight",dpi = 64,
            facecolor = "lightgray", tight_layout = True)
plt.show()

#正規化誤差を求める
sweet_spot = patches.Circle(xy=(0, 0), radius=rad, ec='r',fill=False)
r_sp_ = patches.Circle(xy=(0, 0), radius=r_sp, ec='b',fill=False)
plt.figure()
ax3 = plt.axes()
im3 = ax3.imshow(np.real(NE), interpolation='gaussian',cmap=cm.pink_r,origin='lower', 
               extent=[-Plot_range, Plot_range, -Plot_range, Plot_range],
               vmax=0, vmin=-60)
ax3.grid(False)
ax3.add_patch(sweet_spot)
ax3.add_patch(r_sp_)
plt.axis('scaled')
ax3.set_aspect('equal')
plt.colorbar(im3)
plt.savefig('normalization_error.pdf',bbox_inches="tight",dpi = 64,
            facecolor = "lightgray", tight_layout = True)
plt.show()

まとめ

元々MATLABで作っていたものをPythonで書き直したので変な書き方をしている場所もあるかと思いますが、こうした方がいいよというのがあればコメントお願い致します。

githubにコードあげてます
https://github.com/koseki2580/ambisonics