八戸高専 アドカレ
→2日目
Oklab/Oklchの計算式
モダンなCSSのグラデーションでは、デフォルトでOklab色空間が使用されています。ところで、Oklabってなんぞや???というのを数式とプログラムから見ていきたいと思います。
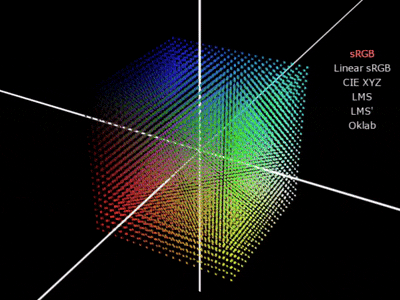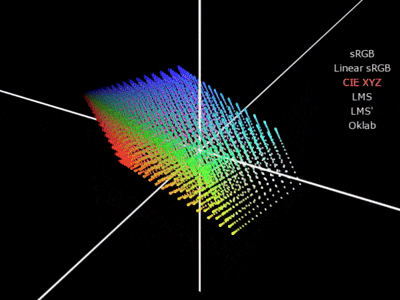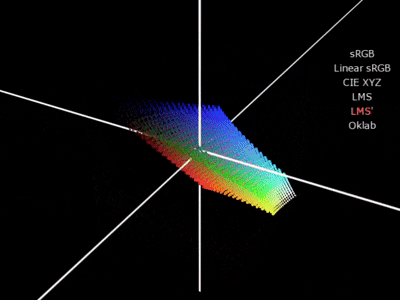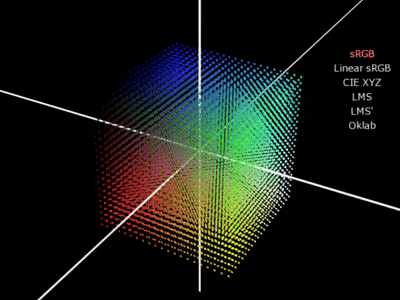
sRGB → Oklab
sRGBをOklabに変換するには、いくつかの色空間を経由します。
1. sRGB → Linear sRGB
sRGBというのは、ガンマ補正(人間の目に合わせた補正)がかけられています。ガンマ補正を外してあげると、物理的な光の特性に即した形(Linear sRGB)になります。
R_\text{linear}=
\begin{cases}\dfrac{R_\text{srgb}}{12.92}, & R_\text{srgb}\le0.04045 \\[5mu]
\left(\dfrac{R_\text{srgb}+0.055}{1.055}\right)^{\!2.4}, & R_\text{srgb}>0.04045
\end{cases}
(G, Bも同様の計算をします。)
2. Linear sRGB → CIE XYZ
可視光領域全体をカバーすることのできる、標準的な色空間(CIE XYZ)に変換します。
\begin{align}
\begin{bmatrix} X_\text{D65} \\ Y_\text{D65} \\ Z_\text{D65} \end{bmatrix} &=
\mathbf M_0
\begin{bmatrix} R_\text{linear} \\ G_\text{linear} \\ B_\text{linear} \end{bmatrix} \\
\mathbf M_0 &= \begin{bmatrix}
0.4124 & 0.3576 & 0.1805 \\
0.2126 & 0.7152 & 0.0722 \\
0.0193 & 0.1192 & 0.9505
\end{bmatrix}
\end{align}
3. CIE XYZ → Oklab
網膜にある3つの錐体細胞が感知する光の波長を考慮した、LMS色空間に変換します。
\begin{align}
\begin{bmatrix} l \\ m \\ s \end{bmatrix} &=
\mathbf M_1
\begin{bmatrix} X_\text{D65} \\ Y_\text{D65} \\ Z_\text{D65} \end{bmatrix} \\
\mathbf M_1 &= \begin{bmatrix}
0.8189330101 & \phantom{-}0.3618667424 & -0.1288597137 \\
0.0329845436 & \phantom{-}0.9293118715 & \phantom{-}0.0361456387 \\
0.0482003018 & \phantom{-}0.2643662691 & \phantom{-}0.6338517070
\end{bmatrix}
\end{align}
LMS(感覚的な色空間)をLMS(物理的な色空間)に補正します。
\begin{bmatrix} l' \\ m' \\ s' \end{bmatrix} =
\begin{bmatrix} l^{1/3} \\ m^{1/3} \\ s^{1/3} \end{bmatrix}
最後に、データセットにより求められた行列を適用します。
\begin{align}
\begin{bmatrix} L \\ a \\ b \end{bmatrix} &=
\mathbf M_2
\begin{bmatrix} l' \\ m' \\ s' \end{bmatrix} \\
\mathbf M_2 &= \begin{bmatrix}
0.2104542553 & \phantom{-}0.7936177850 & -0.0040720468 \\
1.9779984951 & -2.4285922050 & \phantom{-}0.4505937099 \\
0.0259040371 & \phantom{-}0.7827717662 & -0.8086757660
\end{bmatrix}
\end{align}
Oklab → sRGB
OklabからsRGBに変換するには、逆の操作を行います。
1. Oklab → CIE XYZ
\begin{align}
\begin{bmatrix} l' \\ m' \\ s' \end{bmatrix} &= \mathbf M_2^{-1} \begin{bmatrix} L \\ a \\ b \end{bmatrix}, \\
\begin{bmatrix} l \\ m \\ s \end{bmatrix} &= \begin{bmatrix} (l')^3 \\ (m')^3 \\ (s')^3 \end{bmatrix}, \\
\begin{bmatrix} X_\text{D65} \\ Y_\text{D65} \\ Z_\text{D65} \end{bmatrix} &= \mathbf M_1^{-1} \begin{bmatrix} l \\ m \\ s \end{bmatrix}.
\end{align}
2. CIE XYZ → sRGB
\begin{bmatrix} R_\text{linear} \\ G_\text{linear} \\ B_\text{linear} \end{bmatrix} =
\mathbf M_0^{-1}
\begin{bmatrix} X_\text{D65} \\ Y_\text{D65} \\ Z_\text{D65} \end{bmatrix}
3. Linear sRGB → sRGB
R_\text{sRGB} = \begin{cases}
12.92\cdot R_\text{linear}, & R_\text{linear} \le 0.0031308 \\[5mu]
1.055\cdot (R_\text{linear})^{1/2.4}-0.055, & R_\text{linear} > 0.0031308
\end{cases}
(G, Bも同様の計算をします。)
Oklab → Oklch
Oklabはaとbによる直交座標系と見なすことができます。これをcとhによる極座標系にしたのがOklchです。
\begin{align}
c &= \sqrt{a^2 + b^2}, \\
h &= \text{atan2}(b, a)
\end{align}
Oklch → Oklab
\begin{align}
a &= c\cdot \cos(h) \\
b &= c\cdot \sin(h)
\end{align}
プログラム
$\mathbf M'_1= \mathbf M_0 \cdot \mathbf M_1$とすることで、一度の行列計算でLinear sRGBからLMSを求めることができます。
#include <cmath>
struct Lch { float L; float c; float h; };
struct Lab { float L; float a; float b; };
struct RGB { float r; float g; float b; };
float linear(float x) {
if (x >= 0.04045) return std::pow((x + 0.055) / (1 + 0.055), 2.4);
else return x / 12.92;
}
float linear_inv(float x) {
if (x >= 0.0031308) return (1.055) * std::pow(x, (1.0 / 2.4)) - 0.055;
else return 12.92 * x;
}
RGB srgb_to_linear_srgb(RGB c) {
return { linear(c.r), linear(c.g), linear(c.b) };
}
RGB linear_srgb_to_srgb(RGB c) {
return { linear_inv(c.r), linear_inv(c.g), linear_inv(c.b) };
}
Lab linear_srgb_to_oklab(RGB c) {
float l = 0.4122214708f * c.r + 0.5363325363f * c.g + 0.0514459929f * c.b;
float m = 0.2119034982f * c.r + 0.6806995451f * c.g + 0.1073969566f * c.b;
float s = 0.0883024619f * c.r + 0.2817188376f * c.g + 0.6299787005f * c.b;
float l_ = cbrtf(l);
float m_ = cbrtf(m);
float s_ = cbrtf(s);
return {
0.2104542553f * l_ + 0.7936177850f * m_ - 0.0040720468f * s_,
1.9779984951f * l_ - 2.4285922050f * m_ + 0.4505937099f * s_,
0.0259040371f * l_ + 0.7827717662f * m_ - 0.8086757660f * s_,
};
}
RGB oklab_to_linear_srgb(Lab c) {
float l_ = c.L + 0.3963377774f * c.a + 0.2158037573f * c.b;
float m_ = c.L - 0.1055613458f * c.a - 0.0638541728f * c.b;
float s_ = c.L - 0.0894841775f * c.a - 1.2914855480f * c.b;
float l = l_ * l_ * l_;
float m = m_ * m_ * m_;
float s = s_ * s_ * s_;
return {
+4.0767416621f * l - 3.3077115913f * m + 0.2309699292f * s,
-1.2684380046f * l + 2.6097574011f * m - 0.3413193965f * s,
-0.0041960863f * l - 0.7034186147f * m + 1.7076147010f * s,
};
}
Lch srgb_to_oklch(RGB c) {
c = srgb_to_linear_srgb(c);
Lab lab = linear_srgb_to_oklab(c);
return { lab.L, std::sqrt(lab.a * lab.a + lab.b * lab.b), std::atan2(lab.b, lab.a) };
}
RGB oklch_to_srgb(Lch c) {
Lab lab = { c.L, c.c * std::cos(c.h), c.c * std::sin(c.h) };
RGB rgb = oklab_to_linear_srgb(lab);
return linear_srgb_to_srgb(rgb);
}
使用例
カラーピッカーと比較することで、計算が正しいかを確認することができます。
#include <vector>
#include <iostream>
const float PI = 3.141592653589793;
int main() {
std::vector<RGB> ary = {
{229, 16, 59}, //https://oklch.com/#0.5865,0.2306,20.83,100
{31, 124, 221}, //https://oklch.com/#0.5873,0.1694,253.76,100
{182, 220, 66}, //https://oklch.com/#0.8386,0.1792,122.47,100
};
for (int i = 0; i < ary.size(); i++) {
std::cout << "index : " << i;
std::cout << std::endl;
ary[i].r = ary[i].r / 255;
ary[i].g = ary[i].g / 255;
ary[i].b = ary[i].b / 255;
Lch lch = srgb_to_oklch(ary[i]);
std::cout << "L : " << lch.L;
std::cout << ", c : " << lch.c;
std::cout << ", h : " << (lch.h * 180 / PI);
std::cout << std::endl;
RGB rgb = oklch_to_srgb(lch);
std::cout << "R : " << (ary[i].r * 255);
std::cout << ", G : " << (ary[i].g * 255);
std::cout << ", B : " << (ary[i].b * 255);
std::cout << std::endl;
}
return 0;
}
index : 0
L : 0.586541, c : 0.230599, h : 20.829
R : 229, G : 16, B : 59
index : 1
L : 0.586253, c : 0.169519, h : -106.128
R : 31, G : 124, B : 221
index : 2
L : 0.839232, c : 0.17971, h : 122.475
R : 182, G : 220, B : 66
参考
・A perceptual color space for image processing
むすび
Oklab/Oklchの計算式についてでした。